一类典型的无时滞神经网络通过优化控制实现有限时间混合外同步

张 宇

(重庆师范大学 数学科学学院，重庆 401331)



一类典型的无时滞神经网络通过优化控制实现有限时间混合外同步

张 宇

(重庆师范大学 数学科学学院，重庆 401331)

考虑到控制成本是控制领域中一个非常重要的因素，研究了一个典型的无时滞神经网络通过优化控制达到有限时间混合外同步问题. 首先就建立这个问题的优化控制问题，对控制进行优化，是系统达到最低控制成本的有限时间同步，应用控制参数化方法解决优化控制问题. 一个数值例子有效的验证所提出方法.

无时滞神经网络；有限时间混合外同步；优化控制；控制参数化方法

Pecora和Carroll首次提出驱动-响应同步方法[1]，神经网络系统受到了广泛的关注且成功应用到保密通信[2]、模式识别[3]等.迄今为止，混沌神经网络同步的研究方法包括指数同步[4]、渐进同步[5]，也就是说达到平衡点的时间是无限的.在实际的应用中，总是希望快速的达到收敛或是在有限的时间范围内收敛，因此提出了有限时间同步[6].然而很少考虑达到同步时间所需的控制成本.

在网络中的同步，被称为内同步[7]，最近已深入和广泛的研究.同时，一些研究也致力于两个耦合的复杂网络之间的同步，称为外同步.率先研究两个单向耦合的复杂网络之间的外同步[8]，并推导出它们具有相同的拓扑结构.由此，同步的焦点聚焦在两个复杂网络之间不相同的拓扑逻辑结构[9]和两种完全不同的复杂网络[10].近年来，两个复杂网络的混合外同步得到另外深入研究[11-12]，也就是对应节点的不同状态变量可以实现同步、反同步.这些已有的文献中很少考虑实际工程中时间和控制成本的限制.然而在实际系统中控制输出是有限的，并且希望所需的控制输出成本越少越好.

出于以上的考虑，本文旨在分析两个典型的神经网络之间的有限时间混合外同步. 通过构造Lyapunov函数和利用符号函数的性质设计一个反馈控制器，再结合最优化控制技术[13]减少神经网络同步的控制成本且缩短同步时间.

1 模型和准备

考虑两个耦合无时滞神经网络，驱动耦合神经网络和带有控制器的响应神经网络分别如下：

(1)

(2)

其中：i=1,2,…,n,n代表神经元的个数；x(t)=(x1(t),x2(t),…,xn(t))T是t时刻的网络状态向量，f(x(t))=(f1(x1(t)),f2(x2(t)),…,fn(xn(t)))T是t时刻的神经元激活函数；D=diag(d1,d2,…,dn)且ci>0,A=(aij)n×n是连接权矩阵.x(0)=x0和y(0)=y0分别是驱动-响应网络的初值.W(t)=(w1(t),w2(t),…,wn(t))T是控制器.

有限时间混合的误差信号定义为：

ei(t)=yi(t)-(-1)nxi(t),n=1,2,….

(3)

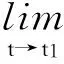
注1 从定义1可以看出混合外同步包括完整的外同步已知的概念，当n为偶数时为完全外同步，当n为奇数是逆外同步，当(-1)n=±1(n=1,2,…)时是混合外同步.

假设1 对任意的x,y∈,x≠y，存在一个常数li(i=1,2,…,n)，使得：|fi(x)-fj(y)|≤li|x-y|.

假设2 非线性函数f(·)满足hifi(xi)=fi(hixi)，hi为常数.

1.1 混合有限时间同步

在这部分中，为了实现混合外同步wi(t)定义为：

wi(t)=-ui(t)sign(ei(t))

(4)

其中ui(t)≥0,sign(ei(t))是符号函数：

其中:u(t)=[u1(t),u2(t),…,un(t)]T，U={u(t):ui(t)∈[0,bi],i=1,2，…,n}，这里bi是ui(t)的上界.因此，U是所有u(t)的集合.因此，误差动力系统可写为：

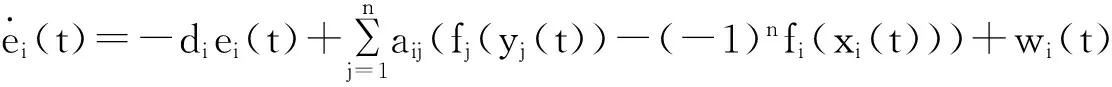
(5)

根据以上分析，以定理1的形式给出如下结果.

定理1 驱动网络(1)和驱动网络(2)在控制器(4)下实现混合外同步，如果下列条件满足：

(6)

其中c>0是一个常数.

证明 考虑如下的Lyapunov函数:

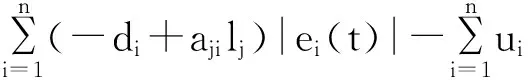
(7)

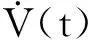
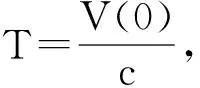
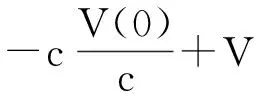
1.2 最小控制成本同步

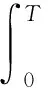
HDFS作为识别系统的文件存储模块,存储着关节点数据、数据预处理的特征数据以及最终的行为分类结果,方便PC端调用的同时为上层Spark计算框架提供数据支撑。

这里F(u)是单调递增的函数，T是稳定时间.在其它一些例子中T又是终端时间.根据以上的内容现在介绍成本函数

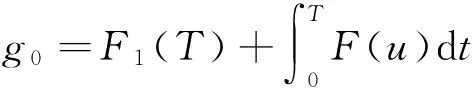
(8)

其中F1(T)是单调递增函数.为了估计最差的稳定时间T，不等式(7)变为等式：

(9)

如果ui(t)是不够大的，系统(9)可能就达不到稳定， 因此就需要增加约束条件V(T)=0.最小成本稳定性问题如下：

问题1 找到个控制向量u∈U，使得(8)最小，动力系统描述为：

约束条件为V(T)=0.

2 优化方法

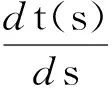
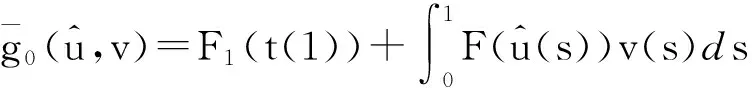
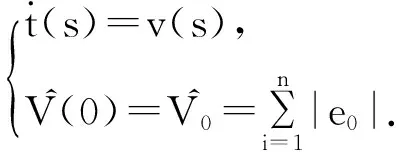
问题1和问题2可以被认为是非线性数学规划问题，其中约束条件和动态系统被认为是约束.它们可以被认为是一般的向量优化问题.然后，使用MISER3[13]这个软件基于梯度的方法来解决这个问题.

3 数字模拟

在这部分中，应用所提出的计算方法来解决以下2个最小控制成本稳定性问题.

例1 考虑下列2维神经网络[14]

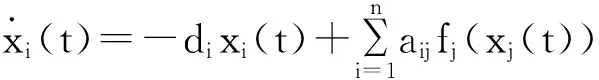
其中：x(t)=(x1(t),x2(t))T，f(x(t))=(tanh(x1(t)),tanh(x2(t)))T，且：

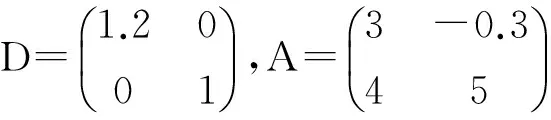
根据定理1和问题2可以建立下列问题：

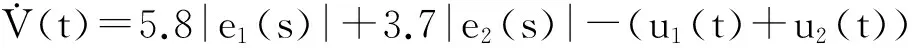
选择初始状态V(0)=5并且F1(T)=log10(T)，F(u)=(0.1·u1(t))3+(0.11·u2(t))3.因此问题1就建立起来了.应用软件MISER3[13]来解决这个问题，并得到优化解，同步时间T=0.461 03s，优化控制成本值1.140 591 02.优化控制函数如图1，V(t)的收敛轨迹如图2.

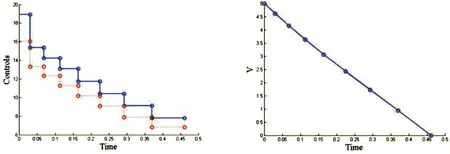
4 结论

本文研究了一类典型的神经网络，在最优化控制方法下实现有限时间混合外同步且降低控制成本.

[1] PECORA L M,CARROLL T L.Synchronization in chaotic systems[J].Physical Review Letters，1990,64(8):821-824.

[2] MILANOVIC V,ZAGHLOUL M E.Synchronization of chaotic neural networks and applications to communications[J].International Journal of Bifurcation and Chaos，1996,6(12b):2571-2585.

[3] HOPPENSTEADT F C, IZHIKEVICH E M.Pattern recognition via synchronization in phase-locked loop neural networks[J].IEEE Transactions on Neural Networks,2000,11(3):734.

[4] SHENG L,YANG H.Exponential synchronization of a class of neural networks with mixed time-varying delays and impulsive effects[J].Neurocomputing,2008,71(16/17/18):3666-3674.

[5] SONG Q.Design of controller on synchronization of chaotic neural networks with mixed time-varying delays[J].Neurocomputing,2009,72(13/14/15):3288-3295.

[6] SHEN J,CAO J.Finite-time synchronization of coupled neural networks via discontinuous controllers[J].Cognitive Neurodynamics,2011,5(4):373-385.

[7] LU J,KURTHS J,CAO J.Synchronization control for nonlinear stochastic dynamical networks:pinning impulsive strategy[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(2):285.

[8] CHI K T.Adaptive synchronization between two complex networks with nonidentical topological structures[J].Phys A,2008,387(2):5623-5630.

[9] MEI J,JIANG M,WANG X,et al.Finite-time synchronization of drive-response systems via periodically intermittent adaptive control[J].Journal of the Franklin Institute,2014,351(5):2691-2710.

[10] WU X,ZHENG W X,ZHOU J.Generalized outer synchronization between complex dynamical networks[J].Chaos,2009,19(1):013109.

[11] WANG J W,MA Q,ZENG L,et al.Mixed outer synchronization of coupled complex networks with time-varying coupling delay[J].Chaos,2011,21(1):013121.

[12] JU H P,KWON O M.LMI optimization approach to stabilization of time-delay chaotic systems[J].Chaos Solitons and Fractals,2005,23(2):445-450.

[13] TEO K.A unified computational approach to optimal control problems[M].New York:Longman Scientific and Technical，1991.

[14] YANG X.Can neural networks with arbitrary delays be finite-timely synchronized?[J].Neurocomputing,2014,143(16):275-281.

责任编辑：高 山

Finite-time Mixed Outer Synchronization for a Class of No Time-delay Neural Networks via Optimal Control

ZHANG Yu

(School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China)

Considering the fact that control cost is a very important factor in control area,we investigate finite-time mixed outer synchronization problem for a class of no time-delay neural networks in this paper.We formulate this problem into an optimal control problem,where the control functions are optimized such that the system can be stabilized with minimum control cost.Then,the control parameterization method is applied to solve this problem.A numerical example is illustrated to show the effectiveness of the proposed method.

no time-delay neural networks;finite-time mixed outer; optimal control;control parameterization method

2017-03-15.

国家自然科学基金项目(61263020).

张宇(1992-)，女，硕士生，主要从事应用数学的研究.

1008-8423(2017)02-0121-04

10.13501/j.cnki.42-1569/n.2017.06.001

O177.91

A