深水到浅水域非线性波传播的数值模型

张文海，贾会杰，王炎

（中交一航局第一工程有限公司，天津300456）

深水到浅水域非线性波传播的数值模型

张文海，贾会杰，王炎

（中交一航局第一工程有限公司，天津300456）

统一方程是在Stokes波理论与Boussinesq型方程相结合的基础上推导出的，适用于深水及浅水域波浪的传播。文中首先分析了统一方程的频散性及其适用性。其次，采用ADI法对控制方程进行离散，并对控制方程中的非线性项进行线性化近似处理，用改进的Patankar半隐格式方法求解动量方程。直接给定入射边界条件，出流边界条件采用Sommerfeld边界条件和消波层相结合的方法，从而建立起从深水到浅水域都有效的数值模型。最后，利用平底与圆形暗礁组合地形上波浪传播的经典物理模型实验来验证数值模型的精确性。将实验结果与数值解相比较，两者吻合较好，说明本文建立的数学模型能有效地模拟水深复杂变化水域波浪传播，具有较高的适用性。

统一方程；数值模拟；消波；非线性波；物理模型实验

0 引言

在引起海岸变形和岸滩演变的众多因素中，波浪为最重要的因素之一。在探索各种适用方法将原属于三维波动问题的竖向坐标变量分离化为二维水平控制方程的过程中，产生了Boussinesq型方程（非线性长波方程）和Stokes波型方程（缓坡方程）这两种用于解决水波问题的控制方程[1]。

Boussinesq型方程属于非线性波的范畴，能较好地描述非线性作用。但只能适用于浅水域。缓坡方程具有完全频散性的特征，属于线性波的范畴，适用于浅水域和深水域，但只适合底坡缓慢变化或者弱的非线性波。虽然国内外众多学者进行了许多改进以扩大其适用范围，但是相伴而来的是方程求解的复杂化。考虑到缓坡方程和Boussinesq型方程两者的优缺点，Li[2]推导了一个不增加额外导数项，适合深水到浅水域波浪传播的统一方程。在有限水深情况下统一方程可化为改进的Boussinesq方程。在深水情况下线性化的统一方程可化为经典波动方程。

1 水深任意变化水域非线性波传播的数值模型

1.1 控制方程及其分析

文献[2]中推导了不增加额外导数项，适用于深水到浅水域非线性波传播的统一方程，假设x、y轴位于静水面，z轴竖直向上，其控制方程为：

式中：η为水面高程；k为波数；g为重力加速度；h为水深；矢量u为水平速度（u，v）；uα为zα处的水平速度矢量，对于规则波传播zα=βh= -0.66h[2]。相比于经典Boussinesq型方程，统一方程式（1）和式（2）没有增加额外的高阶导数项，且非线性项与经典Boussinesq型方程一致。

在浅水域情况下，利用双曲函数的泰勒级数，并忽略高阶导数项O（μ4），函数F1、F2、F3、zαF4可以表示为：

将式（7）、式（8）和式（10）代入到式（1）中，式（9）和式（10）代入到式（2）中，统一方程可以变为：

由上述变换所得式（13）和式（14）和改进的Boussinesq型方程一致（Nwogu 1993[3]；Liu 1995[4]）。因此，在浅水区域中如果忽略高阶项O（μ4），统一方程可转化为改进的Boussinesq型方程。

缓坡方程（Berkhoff 1972[5]）具有完全频散特性，适用于浅水域和深水域，易推广于底坡缓慢变化和弱非线性，但由于是从线性波理论推导而来的，求解强非线性问题相比Boussinesq型方程较差。要求水底坡度较缓和边界波浪的非线性是缓坡方程主要的局限性。而对于统一方程没有这些限制，若以同样的方法建立数值模型，在浅水域中统一方程可以考虑到非线性波的影响，而缓坡方程却不能。

1.2 控制方程的差分格式

小学数学教学情境的创设，要符合不同年龄段儿童的心理特点和认知规律，要根据不同的教学内容有所变化。多年来，通过参加课题研究和教学实践，从在新课引入时、在新知的探究中、在知识巩固上、在整个课堂教学中创设不同的情境，我探索了一些方法，并取得了一些收获：

离散控制方程采用有限差分法，式（1）和式（2）的数值求解是基于空间交错网格系统。对于一个时间步求解统一方程的步骤如下：

1）采用双向扫描法求解动量方程；

2）返回1）进行迭代；

3）用交替方向隐格式法（ADI）求解连续性方程。

控制方程离散格式详见文献[2]。

1.3 波浪传播的边界条件

1.3.1 入射边界条件

本文采用直接给出入射波波面和速度分布作为入射条件，对于不同的地形条件，入射波也不尽相同，本文采用一阶Stokes波理论作为入射边界条件，入射波均为正向入射。其表达式为：

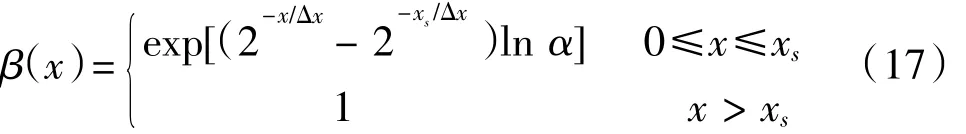
用ηc*代替ηc，用uc*代替uc，再进行下一步计算。

1.3.3 出流边界条件

在计算域的下游边界采用Sommerfeld[8]（1949）边界条件。本文数值模拟中应用于外向波沿向岸边的边界条件可以写为：

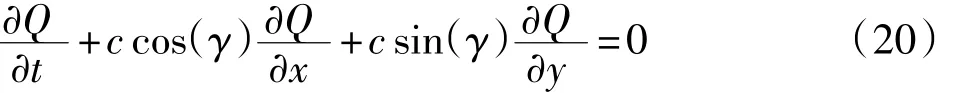
式中：H为入射波波高；h为水深；k为波数；0.34kh是由zα=-0.66h[2]得出的。

1.3.2 入射边界上反射波的消波

直接给定波面和特征流速确定入射边界条件的方法简便直观，但计算域内存在反射或伪反射波时，会导致计算程序的不稳定。因此本文采用张洪生等[6]提出的吸收入射边界上反射波的方法。在离入射边界一定长度区域内设置海绵层，在每一时间步后，变量η和u都要除以指数函数β（x），作者在文献[7]中进行了进一步深化及论证，其表达式为：

式中：Q表示uα、vα和η；c为波速；γ为边界法线方向和出射波的方向之间的夹角。通过假设γ=0，式（20）有不同的有限差分格式。本文采用的方法为：

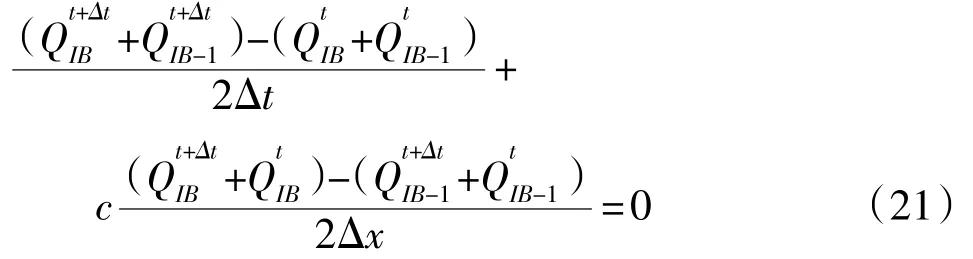
式中：IB代表边界网格点。

2 均匀水深水域波浪传播的数值模拟

为了验证统一方程的适用性，就均匀水深水域中波浪的传播进行了系统的数值模拟。设置长度为85 m的水槽，在水槽左端采用二阶Stokes波作为入射条件，右端为自由出流的开边界。为了进行系统的数值模拟，设置固定波周期T=2.0 s，分别模拟了kh=1、kH=0.2，kh=2、kH=0.3，kh=3、kH=0.4，kh=100、kH=0.5四种组合情况。在数值计算过程中，空间步长取为Δx= 0.05 m，时间步长取为Δt=0.025 s，数值模拟结果如图1所示。

图1计算值与二阶Stokes波理论值的比较Fig.1Comparison of numerical results with Stokes second-order wave

图1 为各计算组合情况下相对高程沿程变化的过程线，可以看出在不同水深、不同参数的情况下数值解与理论解都吻合良好。表明均匀水深情况下模型对深水域波在较长的时间和传播距离内可进行稳定准确地数值模拟。因此统一方程可适用于模拟浅水到深水几乎整个水域弱非线性波的传播。

3 平底与圆形暗礁组合地形上波浪传播的数值模拟

Ito 1972[9]对平底与圆形暗礁组合的地形上的波浪传播进行了物模实验，这一物理模型试验是检验数学模型精度的经典试验之一，试验地形见图2。

图2 Ito物理模型试验示意图（单位：m）Fig.2Sketch of physical experiment by Ito（m）

入射波周期T为6.3 s，波高为1.0 m，上边界为自由出流的开边界，侧边界为全反射的固壁边界。选取空间步长为L0/14，时间步长为T/32，数值模拟结果如图3～图6所示。

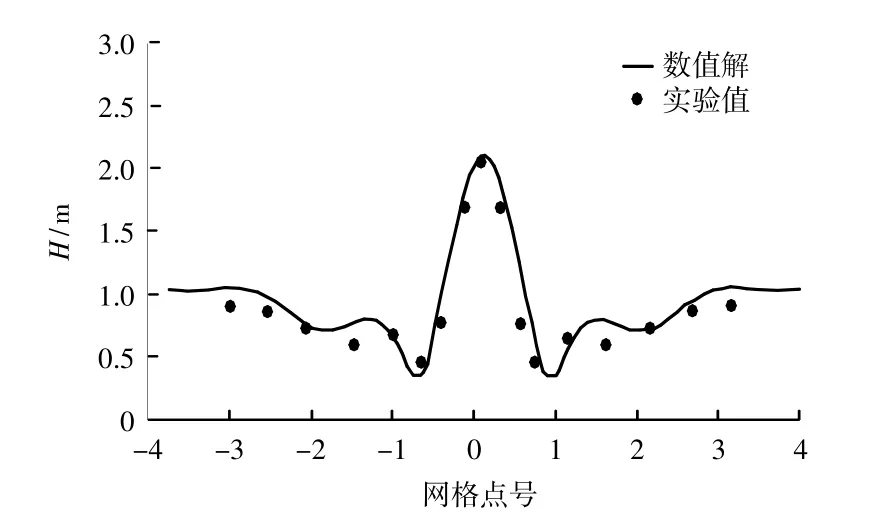
图3 相对波高的计算结果与实验数据比较图（a断面）Fig.3Comparison of computational results with experimentaldata of relative wave height(Section a)

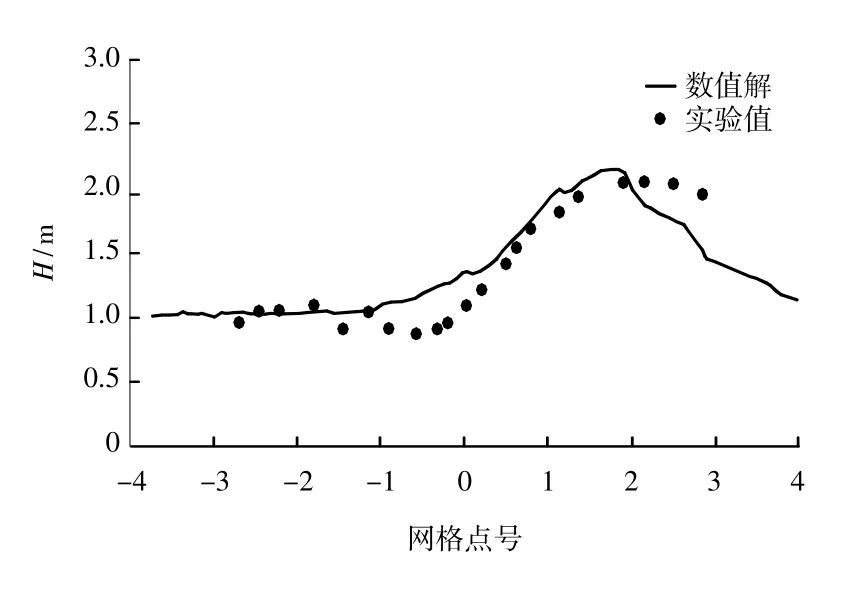
图4 相对波高的计算结果与实验数据比较图（b断面）Fig.4Comparison of computational results with experimental data of relative wave height(Section b)

图5 不同测点处波面随时间变化的数值解Fig.5Numerical Simulation of wave surface changing with time at various positions

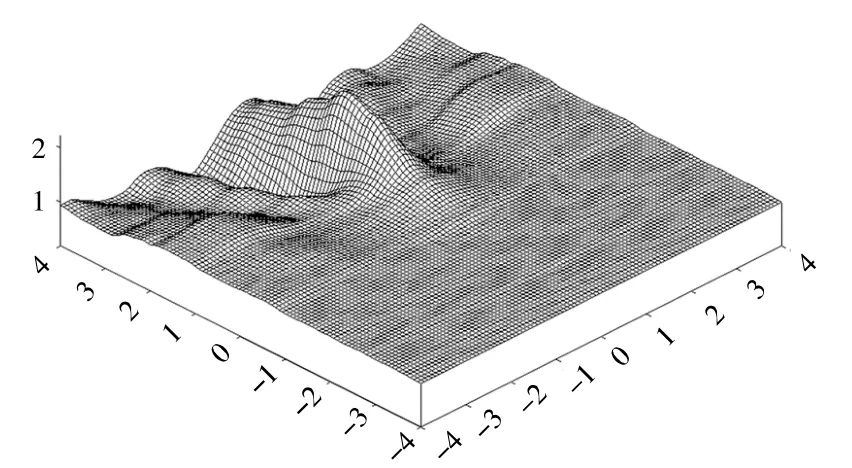
图6数值模拟的波高立体图Fig.6Wave height stereogram of numerical simulation

图3 、图4分别是a、b断面处的相对波高，由图可见数值解与实验值吻合良好。图5为A、B、C、D四个点的波面随时间变化过程曲线图，由图可以看出波动过程随时间变化十分稳定，说明计算结果可靠。深水点A处波形呈余弦波，波谷和波峰对称。由于横断面上中心凸起，在由深水到浅水（B向C）的传播过程中，波高沿程逐渐减小，出了圆形暗礁后的平坦水域，水槽中心线的波高沿程逐渐增加。图6为数值模拟的波高立体图。通过数值计算结果与物模试验值的比较表明，此数值模型能够有效地模拟复杂变化地形上的波浪传播。

4 结语

相比于Boussinesq型方程和缓坡方程这两种基本方程，统一方程显著的改进是其能准确的满足规则波在深水和浅水域的频散关系，其浅化梯度系数与适合深水域的Stokes波理论值吻合良好。若忽略高阶项O（μ4），在浅水情况下统一方程可化为改进的Boussinesq型方程。本文以统一方程为控制方程，基于空间交错网格系统对其进行数值求解，采用交替方向隐格式法（ADI）求解连续性方程，用改进的Patankar（1980）半隐格式方法求解动量方程，从而建立了新的数值模型。在给定初始条件和入射边界条件后，采用Sommerfeld型边界条件和消波层相结合的方法处理出流边界。采用两者相结合的边界条件，能够有效地吸收波浪的能量，消除或者减少波浪能量的反射，从而保证数值模拟的精度。利用Ito对平底与圆形暗礁组合的地形上波浪传播的物模实验对数值模型的精度及适用性进行验证。两者吻合良好，表明本文所建立的数值模型可以较为有效地模拟水深复杂变化地形上非线性波的传播与变形，具有较高的适用性。本模型未考虑波浪水流等对波浪变形的影响，这有待于进一步的探讨和改善，其对近岸工程、远海生产作业、近岸环境保护等方面具有十分重要的意义。

[1]张洪生.非线性波传播的数值模拟[D].南京：河海大学，2000.

ZHANG Hong-sheng.Numerical modeling of nonlinear wave propagation[D].Nanjing:Hohai University,2000.

[2]LI B.Wave equations for regular and irregular water wave propagation[J].Journal of Waterway,Port,Coastal and Ocean Engineering, 2008,134(2):121-142.

[3]NWOGU O.Alternative form of Boussinesq equations for nearshore wave propagation[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1993,119(6):618-638.

[4]LIU L F,CHO Y S,BRIGGS M J,et al.Runup of solitary waves on a circular island[J].Journal of Fluid Mechanics,1995,302:259-285.

[5]BERKHOFF J C W.Computation of combined refraction-diffraction [C]//Proceedings of 13th conference on coastal engineering,ASCE, 1972:471-490.

[6]张洪生，商辉.对波浪入射边界上反射波的消波及其验证[J].上海交通大学学报，2008，42（4）：674-678.

ZHANG Hong-sheng,SHANG Hui.A method of absorbing the reflectedwavesonincidentboundaryand its verification[J].Journal of Shanghai Jiaotong University,2008,42(4):674-678.

[7]ZHANG Hong-sheng,WANG Yan,XU Chun-hui,et al.Tests and applications of an approach to absorbing reflected waves towards incident boundary[J].China Ocean Engineering,2013,27(6):703-718.

[8]SOMMERFELDA.Partialdifferentialequationsinphysics: lectures on theoretical physics,Vol.6[M].Salt Lake City,UT: Academic Press,1949.

[9]ITO Y,TANIMOTO K.A method numerical analysis of wave propagation application to wave diffraction and refraction[C]/Proceedings of 13th conference on coastal engineering,ASCE,1972: 503-522.

Numerical modeling of nonlinear wave propagation from deep water to shallow water

ZHANG Wen-hai,JIA Hui-jie,WANG Yan
（No.1 Engineering Co.,Ltd.of CCCC First Harbor Engineering Co.,Ltd.,Tianjin 300456,China）

The unified equations are derived from the Stokes second-order wave theory and the Boussinesq-type equations.It is suitable for the propagation of waves in deep and shallow seas.We firstly analyzed the dispersion and applicability of the unified equations,then used the ADI method to disperse the governing equations,processed the nonlinear terms of the governing equations by linear approximation,and used the modified Patankar with semi-implicit schemes to solve the momentum equations.Given the boundary conditions,the outflow boundary conditions are combined with the Sommerfeld boundary condition and the wave elimination layer,so as to establish a valid numerical model suitable for wave transformation from deep water to shallow water.At last,the experiment data from physical model of wave propagation and deformation in the complicated water is used to verify the accuracy of present numerical model.The experimental results are in good agreement with those of numerical solution.It indicates that the numerical model can effectively simulate the wave propagation in the water with varying topography,and has a high applicability.

unified equations;numerical simulation;absorbing waves;nonlinear wave;physical experiment

U651.3；P731.2

A

2095-7874（2017）06-0036-05

10.7640/zggwjs201706008

2017-01-25

2017-04-14

张文海（1976—），男，天津市人，高级工程师，副总经理，港航工程专业。E-mail：33162727@qq.com