基于栅格法的移动机器人路径规划研究

蒋浩+杨子江+储旭+孙卓荦

摘要：在环境已知或易于获得的前提下，利用栅格法对环境进行建模，建立机器人定位的数学模型，并对机器人的路径规划算法问题进行分析，最后介绍两种优化的路径搜索算法。

关键词：路径规划；栅格法；机器人定位；优化算法

0引言

移动机器人在现代生产生活中扮演着日益重要的角色，在制造业、服务业中的应用给人们的生活带来了极大的便利[1]。移动机器人的路径规划问题始终是研究的热点和难点，所谓机器人路径规划，是指在已知、部分已知或未知工作环境信息的情况下，机器能够按照设定的任務要求，依据自身或全局传感器获得的数据信息，对自身位置以及当前环境进行辨识，通过相应的算法，自主规划出从起始点到达目标点的最优路径，同时要满足安全、无碰撞等性能指标。

移动机器人的路径规划主要由环境建模、路径搜索两部分组成。路径规划的方法有很多，通常根据其所适用的工作环境的不同划分为全局路径规划方法和局部路径规划方法。全局路径规划多用于工作环境已知的情况，典型方法有栅格法和拓扑法等；局部路径规划则常用于未知环境下移动方案设计，常用方法有模糊逻辑法、人工势场法、神经网络算法等[2]。本文采用栅格法进行环境建模，并基于此介绍一些常用的路径搜索算法。

1移动机器人定位

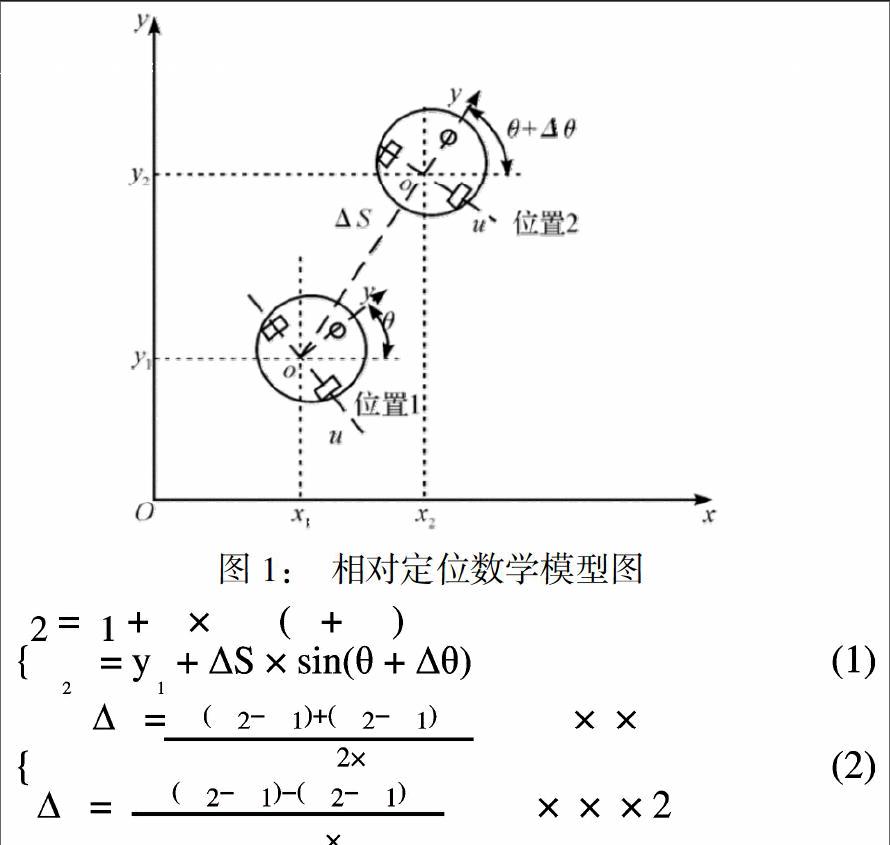
机器人移动动作主要为前进，后退，左转，右转。借助编码器和陀螺仪，对基于双驱动移动的机器人模型运动分析如图 1 所示[3]（假设车轮不打滑、车身为刚体）：

式（1）、（2）中：W 为两轮间距，D 为两轮直径，θ 为绝对坐标机器人的走向，S 为两个位置机器人的移动距离，x 为横坐标，y 为纵坐标，a 为编码器转一圈的脉冲数，ml 为左轮编码器返回的脉冲数，mr 为右轮编码器返回的脉冲数。左、右编码器读出返回的脉冲数 ml 和 mr，陀螺仪读取 θ+ θ 的角度值，上式即为相对定位的坐标计算公式。

2栅格法

在路径规划问题中，需要将机器人当作质点来处理，以减少运算；描述障碍物时需要考虑一定的安全距离，这个安全距离与移动机器人的尺寸相关；由于移动机器人是在一个二维平面空间里运动，不需要考虑障碍物的高度信息。在已知环境基础上，由于很容易得到全局坐标系，采用栅格法进行环境建模是最为适用的。栅格法路径规划一般分为三个步骤[4]：

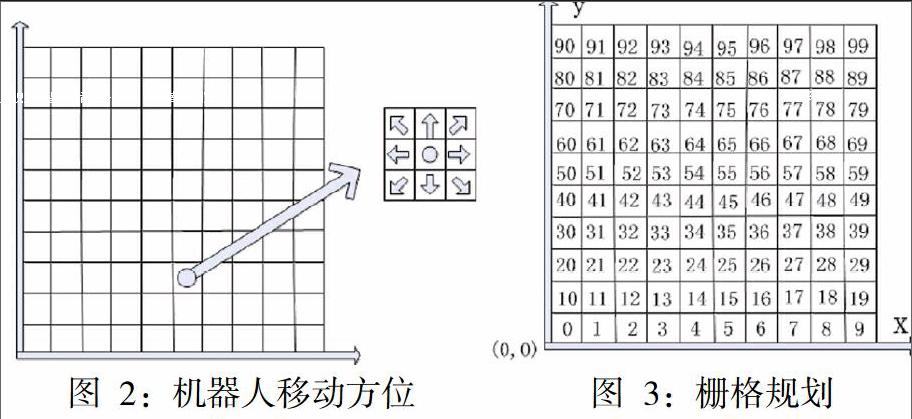
（1）建立模型：它把移动机器人所在的二维平面空间划分为一些列大小相同的矩形栅格。地图中，供机器人移动的方向有八个，如图 2 所示。栅格大小的确定是栅格法的首要问题，障碍物表示的精确程度跟栅格大小成正比关系，但栅格过于精细时，需要耗费大量的存储空间，并影响处理速度。因此要考虑机器人尺寸、精度等多方面因素。在全局坐标系下进行栅格化，给每一个栅格标记序号，从开始进行标记，且每个栅格的中心点都有相应的坐标，如图 3 所示：

在规划栅格后，需要将其转换为坐标系中的点。第 A 个栅格的坐标为：

{ = /2 + % × （3） = D / 2 + [A/COL] ×

式（3）中 为每个栅格的宽度，D 为每个栅格的高度。ROW 为每一行的栅格数，COL 为每一列的栅格数。利用对机器人定位获得的数据，通过一定的计算，也可得到机器人所处的栅格号。

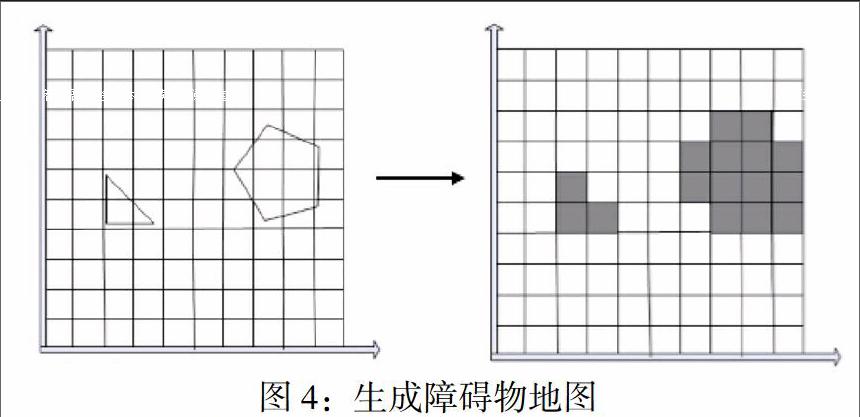
（2）生成障碍物地图：栅格模型建立完成后，将开始对障碍物的位置进行相关检测，并根据障碍物的位置确定所对应栅格地图中的序号，然后进行修改对应序号的栅格值，并将不包含障碍物的那部分栅格归为自由栅格，包障碍物的那部分栅格归为障碍物栅格。考虑到障碍物的形状不规则，人为对障碍物的标记做一下定义：①在两个障碍物之间的距离小于机器人尺寸时，合并成一个障碍物；②进行栅格处理时，需要进行扩大处理，将拥有部分障碍物的栅格全部标记。为方便记录，我们将有障碍物的地方标记为1，无障碍物的地方标记为0。示意图如下：

标记后就会形成集合可表示的障碍物群集。

（3）最优路径规划：即寻找一条满足设计要求的机器人能够连续自由、无碰撞移动的栅格道路。已有很多路径规划算法可供使用，如蚁群算法、人工势场法、遗传算法、快速随机树等。

3两种路径搜索算法优化

一、栅格法与遗传算法的结合遗传算法[5][Genetic Algorithms] 是当代人工智能科学的一个重要研究分支，是一种模拟达尔文遗传选择过程中的计算模型。它是按照基因遗传学原理而实现的一种迭代过程的随机搜索算法。遗传算法具有智能性，智能表现在自组织、自适应和自学习的能力； 遗传算法具有并行性， 一是内含并行性， 二是搜寻对同一问题的最优解上，可以利用若干计算机同时进行搜索计算。在激光导航定位仪的应用中，全局坐标系的建立以及障碍物的描述都变得相对容易。利用硬件测量环境信息，通过栅格法完成对环境进行建模以及障碍物的栅格表示，然后利用遗传算法高并行处理全的优势作为路径优化和搜索，最终获得最优路径。

二、栅格法与蚁群算法的结合蚁群算法[4][Ant Colony Algorithm]，简称 ACA）的思想来自于对蚁群觅食行为

的探索，每个蚂蚁觅食时都会在走过的道路上留下一定浓度的信息素，相同时间内最短的路径上由于蚂蚁遍历的次数多而信息素浓度高，加上后来的蚂蚁在选择路径时会以信息素浓度为依据，起到正反馈作用，因此信息素浓度高的最短路径很快就会被发现。算法通过迭代来模拟蚁群觅食的行为达到目的。具有良好的全局优化能力、本质上的并行性、易于用计算机实现等优点，但计算量大、易陷入局部最优解。在传统的蚁群算法中，有效路径规定为能够从起点到达终点的单向路径，限制了蚁群间的协调作用。为提升搜索效率，可在栅格法基础上使用两组蚂蚁进行双向搜索的方法来构建最优路径。双向搜索过程中，两个规模相同的蚁群分别从起点和终点出发，会出现寻优起点方向不同的两只蚂蚁相遇（包含同时相遇和不同时通过同一点两种情况），通过结合两只相遇的蚂蚁各自携带的不同的内在搜寻信息，连接它们所行走的路径的方法构造成为一条可行的路径。

4结束语

本文利用相对定位方法为移动机器人的路径规划提供了思路。对栅格法进行了较为详细的说明，同时介绍了基于栅格法的遗传算法和蚁群算法的优化实现，具有一定的参考价值。随着科研的深入发展，栅格法会在路径规划中得到越来越多的应用。

参考文献：

[1]蔡自兴，郭璠. 中国工业机器人发展的若干问题[J]. 机器人技术与应用，2013，（03）：9-12.

[2]张广林，胡小梅，等. 路径规划算法及其应用综述 [J] 现代机械，2011（5）：85-89

[3]尹力伟，梅志千，谢保春，等. 基于 MRDS 的清洁机器人室内路径规划算法的仿真实现[J]机电工程，2014， 31（11）：1505-1506

[4]周磊. 改进蚁群算法在机器人路径规划中的应用研究[D].华东理工大学硕士学位论文，2012：20-21

[5]朱天宇.移动机器人路径规划的研究[D].重庆大学硕士学位论文，2014：25-31