K—means和人工鱼群结合的聚类算法研究

仇桦+周莲英

摘要：针对Kmeans算法对初始聚类中心敏感、容易收敛于局部極值和人工鱼群算法最大步长固定、寻优精度不高、后期收敛速度慢的问题，提出一种Kmeans和人工鱼群相结合的聚类算法。该算法将Kmeans聚类中心引入人工鱼群适应度函数，自动确定近似全局最优的初始聚类中心，并将其作为Kmeans初值详细进行局部搜索，以提高精度。同时采用淘汰机制和自适应的最大步长策略，优化人工鱼群算法性能。在Iris、Wine数据集和EPA-HTTP应用日志数据上对IAFSAKM算法进行实验仿真分析，验证了算法的有效性和可行性。

关键词：Kmeans；人工鱼群算法；聚类；淘汰机制；自适应策略DOI：10.11907/rjdk.162799中图分类号：

文献标识码：A

文章编号：16727800（2017）004005504

0引言 数据聚类是静态数据分析技术，目标是将数据集合分成若干簇，使得同一簇内的数据点相似度尽可能大，而不同簇间数据点相似度尽可能小。目前在数据挖掘[1]、机器学习[2]、人工神经网络[3]、图像分析[4]、模式识别[5]以及无线传感器网络[6]等领域应用十分广泛。Kmeans算法[7]是其中最著名也是最简单的一个聚类方法，能有效解决许多聚类问题。但是聚类算法有两大缺陷：①对初始点敏感；②易陷入局部最优。 人工鱼群算法（Artificial Fish Swarm Algorithm， AFSA）是一种基于仿生行为的群体智能全局寻优算法 [8]，具有收敛速度快、对初始值不敏感、灵活性好及较高的容错率等一系列优点，能较好地解决优化问题，然而，单一的聚类方法往往得不到最佳聚类效果。 针对该问题，本文在改进的人工鱼群算法基础上结合Kmeans聚类算法，提出了一种新的混合聚类算法IAFSAKM：先将引入了淘汰机制和自适应最大步长策略的人工鱼群算法（IAFSA）对Kmeans的聚类过程进行优化。用一条人工鱼表示一次选择的k个初始聚类中心，把Kmeans的聚类中心引入取误差平方和函数倒数的适应度函数，人工鱼在寻优过程中自动确定全局近似最优的聚类中心。该方法弥补了Kmeans算法对初始中心敏感、容易收敛于局部极值的缺点；然后将该聚类中心作为Kmeans的初始中心进行局部搜索，利用Kmeans的快速收敛性，进一步提高寻优精度。在Iris和Wine数据集和EPA-HTTP应用日志数据上进行对比实验，证明了该算法的有效性和可行性。

1Kmeans聚类算法

Kmeans算法[9]是一种基于划分的聚类分析方法。聚类中心个数k是一个给定的正整数，P={P1，P2，…，Pn}是一个具有n个数据样本的数据集，其中Pi={Pi1，Pi2，…，Pim}表示数据集中具有m个属性的m维样本。Kmeans算法以欧式距离作为相似性度量标准，遵循类内相似度高和类间相似度低的原则，相似度计算则根据类中对象的平均值进行。聚类问题就是要找到k个聚类中心C={C1，C2，…，Ck}，使得数据集中的每个数据样本都属于一个类，且仅属于一个类。假设Ci={Ci1，Ci2，…，Cim}，Pj∈Ci，则Pj到Ci的欧式距离为D（Pj，Ci）=〖JP3〗〖KF（〗（Pj1-Ci1）2+（Pj2-Ci2）2+…+（Pjm-Cim）2

。Kmeans算法是使各样本点到各自类中心的欧式距离和最小。Kmeans算法易于描述，具有时间效率高且适于处理大规模数据等优点，但却存在需要预先确定k值、受初始聚类中心影响以及容易收敛于局部最优解等不足。〖BT1〗〖STHZ〗〖WTHZ〗2人工鱼群算法（AFSA）及其改进人工鱼群算法[10]是一种基于动物行为的群体智能算法，它通过模拟鱼群的随机、觅食、聚群、追尾等行为，相互协作来达到问题的最优解。算法主要包括觅食行为、聚群行为、追尾行为，可控参数包括鱼群规模—N、鱼的视野即搜索范围—visual、鱼的步长即每次可移动的最远距离—step、拥挤度因子—δ、尝试次数—try_number、算法的适应度函数—Y=f（X），即人工鱼当前所在位置的食物浓度等。〖BT2〗〖STHZ〗〖WTHZ〗2.1人工鱼群算法实现每条个体鱼都能自行或尾随其它人工鱼找到富含食物的地方，所以通常鱼生存较多的地方就是富含营养最多的地方。依据这一特点来模仿鱼群觅食、聚群及追尾行为，实现寻优，这就是人工鱼群算法的基本思想。人工鱼群算法步骤如下：（1）初始化人工鱼群算法参数。参数包括鱼群规模、视野范围、步长、人工鱼初始位置、最大迭代次数、尝试次数、拥挤度因子等。（2）更新每条人工鱼位置。如果满足对应条件，则按下列规则动态更新人工鱼的位置信息：设人工鱼当前状态为Xi，根据条件执行如下行为操作：觅食行为：觅食就是鱼趋向食物的行为。当前人工鱼在视野visual范围内随机选择一个状态Xj，其中Xj=Xi+rand（）×visual，式中rand（）函数为0～1之间的随机数，执行以下操作：

2.2人工鱼群算法改进人工鱼群作为一种随机搜索算法，在聚类问题中无需预先设置聚类中心和类别个数，表现出强鲁棒性和高效率特性。人工鱼群算法的计算复杂度与种群规模有关。随着个体数量增加，存储空间随之增多，计算时间也随之延长。在寻优后期，大步长会让人工鱼在全局极值区域来回震荡，影响寻优精度，小步长则会降低算法的收敛速度。针对以上两个参数对人工鱼群算法性能产生影响的问题，本文引入淘汰机制优化计算复杂度，提出自适应最大步长策略，优化收敛速度和寻优精度[11]。

2.2.1基于淘汰策略的计算复杂度优化人工鱼群算法经过一定量的迭代后，适应度小的鱼对算法性能影响不大，本文引入淘汰机制。该机制的思想来自于自然界“弱肉强食”现象，即弱小的鱼会被强大的鱼吃掉。通过引入淘汰机制减少种群数量，实现降低算法计算量的目的。本文引入一个新的参数θ，约定经过最大迭代次数的一半后，计算式（5）的值。式中Ymax、Ymin表示一次迭代中最大、最小适应度值，Yi表示与Ymax、Ymin同一次迭代中第i条人工鱼的适应度。将Ti与θ比较，若Ti小于θ，就淘汰对应的人工鱼，此时鱼群规模会相应减少。在设置淘汰机制中的参数θ时需对适应度函数最优状态有一定了解。本文对Yi作归一化处理，得到的Ti是适应度函数值的比例形式。设置参数θ是一个小于1的正数，以提高淘汰机制在优化问题中的适用性。

2.2.2基于自适应最大步长的收敛速度和寻优精度优化本文引入自适应的最大步长概念，在寻优初期，给人工鱼设置最大步长，尽可能快地找到全局极值区域，提高算法收敛速度。在寻优后期，给人工鱼设置最小步长，以提高算法的寻优精度。自适应最大步长公式如式（6）、式（7）所示，IT为最大迭代次数，α是一个常数，t表示第几次迭代。公告牌除了记录最优人工鱼状态之外，还增加了迭代次数和同一次迭代中最小适应度值。

3 融合Kmeans和人工鱼群的聚类算法IAFSAKM 鱼群算法和聚类分析问题有着天然的对应关系[12]，因此将人工鱼群算法引入聚类分析领域。IAFSAKM算法结合了人工鱼群算法和Kmeans算法优点，既能克服算法对于初始聚类中心选择敏感的问题，又能提高人工鱼群后期收敛速度，能够在较短的时间内获得最优的聚类划分。

3.1IAFSAKM算法实现人工鱼群算法AFSA的每个解由人工鱼的位置和该位置的适应度值两部分组成，如式（8）所示。在解决组合优化问题时，要根据目标函数和变量特点确定合适的位置和适应度函数。

3.2人工鱼位置编码结构人工鱼群算法AFSA在搜索空间内对适应度函数寻优时，一条人工鱼是一个潜在的解；Kmeans算法在给定的数据集上对误差平方和寻优时，选定的k个初始聚类中心是一个潜在的解。因此，可以在人工鱼和k个初始聚类中心之间建立一种映射关系，对人工鱼位置结构编码，本文使用实数编码方式。对人工鱼位置结构编码，用一条人工鱼代表一种聚类方案。人工鱼群算法在迭代前先随机初始化n条人工鱼。对于Kmeans 算法而言，就是随机给出n种初始聚类中心，这n种聚类中心其实是n种聚类方案。人工鱼执行行为就是从n种聚类方案中选择最优的一种。人工鱼编码结构表示如下：

3.3适应度函数本文在介绍人工鱼群算法AFSA时均以极大值为例，误差平方和函数是要被最小化的，因此取误差平方和函数的倒数作为人工鱼群算法AFSA的适应度函数，这样就把聚类中心引入到人工鱼群算法AFSA的适应度函数中。适应度函数表示为式（10）：

J是误差平方和函数，m为常数，k为聚类中心个数，Ci是聚类中心，xj是数据对象。使用下面的方法计算人工鱼适应度：①根据距离最短原则，确定一条人工鱼个体代表的聚类划分；②根据步骤①的聚类划分计算误差平方和函数值和新的聚类中心；③根据步骤②误差平方和函数值，由式（10）计算人工鱼个体的适应度。由上面3个步骤可知，如果一条人工鱼的适应度最大，就说明这条鱼代表的聚类划分误差平方和最小。表1是人工鱼编码。

3.4IAFSAKM算法实现 Kmeans和人工鱼群相结合的IAFSAKM算法[13]步骤如下：①设置参数。设置鱼群规模、视野、步长、尝试次数、拥挤度因子、Kmeans和人工鱼群算法的最大迭代次数、聚类数目，常数m取值为1；②初始化鱼群，计算所有人工鱼适应度，记录最优个体状态；③对每条人工鱼评估行为，尝试执行觅食、聚群、追尾、随机这4种行为，选择适应度最大的行为执行；④更改位置或淘汰人工鱼，计算新位置的适应度，更新最优状态；⑤如果达到最大的迭代次数就结束迭代，输出最优解。反之返回步骤③；⑥把IAFSA的输出作为Kmeans的初始聚类中心；⑦计算数据对象相似度并归类。使用欧式距离计算剩余的数据对象与中心的相似度。根据距离最短、相似度最大原则，把数据对象划分到距它最近的聚类中心所属类；⑧计算误差平方和函数值与新的聚类中心。新的聚类中心由一个类内所有点的算术平均值表示；⑨判断：准则函数值满足一定条件或达到迭代次数，算法结束。当前中心点就是要输出的结果。否则返回步骤⑦继续执行。Kmeans和人工鱼群相结合的IAFSAKM算法流程如图1所示。

4实验仿真与分析

表2显示两种算法性能指标比较结果，这些结果是程序独立运行15次取平均之后的值。其中BV表示最优解，MBV表示平均最优解，MSG表示寻优成功的平均迭代次数。从表中可知，改进后的算法三项性能指标较优，BV和MBV值小表明算法的寻优精度高，MSG低表明寻优速度快。〖HJ*3〗可见，引入淘汰机制和自适应的最大步长策略的人工鱼群算法计算量较低，收敛速度较快，同时保证了算法精度。 为了更直观地反映新算法的聚类效果，本文从标准数据集UCI中选择Iris和Wine两个真实数据集来验证IAFSAKM算法性能。 Iris：以鸢尾花的特征作为数据来源，数据集包含150个样本，分为3类，每类有50个包含4个属性的数据，是数据挖掘、数据分类中常用的测试集、训练集。 Wine：葡萄酒识别，以178个样本分成3个不同的类，分别包含13个属性的59、71和48个样本。 人工鱼群算法各参数设置如下：N=30，step=1，δ=8，visual=2.5，try_number=50，阈值为0.3，迭代次数为100。 本文用聚类准确率衡量算法性能，准确率用被分配到正确簇的数据元素个数与总数据元素个数的百分比表示。由所选数据集可知，聚类数目为3，每一次随机选择3个点作为Kmeans和IAFSAKM算法的初始中心点，共选择15次。本文约定设置最大迭代次数作为Kmeans算法的终止条件，取最大迭代次数为50。算法在运行15次后得到的平均准确率如表3所示。

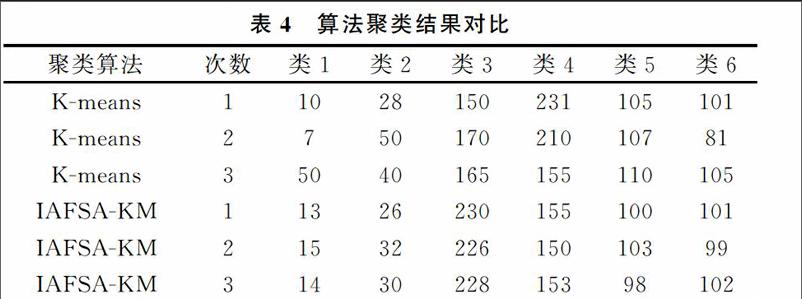
從表3数据可知，IAFSAKM算法可以处理低维、也可以处理高维数据集。在15次随机选择初始点情况下，IAFSAKM的平均准确率高于Kmeans。这说明IAFSAKM算法用于聚类时得到的聚类结果稳定，可见IAFSAKM算法对初始中心点不敏感，实现了全局寻优。 EPA-HTTP日志数据是互联网流量文库Trace数据中的一类。日志数据共47 748条日志记录。每一条日志信息属性有：IP或域名、访问时间、请求方式、请求地址、HTTP协议类型、状态码、返回信息大小。对日志数据预处理（数据清洗、用户识别、会话识别、事务识别）得到用户访问向量集，使用Canopy算法粗略确定聚类数目为6，迭代次数设置为100；使用IAFSAKM算法对用户访问向量集聚类，每一次随机选择6个用户向量作为IAFSAKM和Kmeans的输入，共选择3次。每个类的用户向量数目如表4所示。

可以看到在确定聚类数目后，Kmeans得到的类中向量数目变化较大，不稳定；IAFSAKM算法得到的类中向量数目变化小，比较稳定。这说明本文提出的IAFSAKM算法不依赖初始中心点，解决了Kmeans算法在聚类时很难收敛到全局最优解问题，提高了聚类准确度。

5结语 本文针对Kmeans算法及人工鱼群算法各自的优缺点，提出一种融合Kmeans和人工鱼群的数据聚类算法IAFSAKM。在此算法中，首先根据鱼群规模和步长两个参数对人工鱼群算法的影响，引入淘汰机制和自适应的最大步长策略。淘汰策略中对适应值作归一化处理，设置的参数为一个小于1的比例值，使用多极值函数验证了本文改进算法，结果表明本文算法可以降低复杂度，提高收敛速度和寻优精度。其次，完成人工鱼位置结构编码和适应度函数设计。使用Iris和Wine数据集、EPA-HTTP日志数据对IAFSAKM算法进行验证。实验表明，IAFSAKM算法对初始聚类中心不敏感，可以实现全局寻优，聚类准确率高，结果稳定。参考文献：[1]DATTA SOUPTIK，GIANNELLA CHRIS，KARGUPTA HILLOL，et al.Approximate Distributed KMeans clustering over a peertopeer network [J].IEEE Transactions on Knowledge and Data Engineering，2009，21（10）：13721388.

[2]YANG X L，SONG Q，ZHANG W B.Kernelbased deterministic annealing algorithm for data clustering [J] .IEEE Proceedings on Vision，Image and Signal Processing，2007（153）：557568.

[3]AJIT K SAHOO，MING J ZUO，MK TIWARI， et al. A data clustering algorithm for stratified data partitioning in artificial neural network [J].Expert Systems with Application，2012，39（8）：70047014.

[4]GONG M，LIANG Y，SHI J，et al.Fuzzy CMeans clustering with local information and kernel metric for image segmentation[J].IEEE Transactions on Image Processing，2013，22（2）：573584.

[5]ZHANG L J，CHENG S，CHANG C K，et al.A Patternrecognitionbased algorithm and case study for clustering and selecting business services [J].IEEE transactions on systems，man，and cybernetics.Part A，Systems and humans，2012，42（1）：102114.

[6]ALI PEIRAVI，HABIB RAJABI MASHHADI，S HAMED JAVADI，et al.An optimal energyefficient clustering method in wireless sensor networks using multiobjective genetic algorithm [J].International journal of communication systems，2013，26（1）：114126.

[7]HAN JIAWEI，MICHELINE K.數据挖掘概念与技术[M].范明，孟小峰，译.北京：机械工业出版社，2001.

[8]杨淑莹，张桦.群体智能与仿生计算： Matlab技术实现[M].北京：电子工业出版社，2012： 110.

[9]肖琪. 基于优化Kmeans算法的电力负荷分类研究[D].大连：大连理工大学，2015.

[10]李晓磊. 一种新型的智能优化方法人工鱼群算法[D].杭州：浙江大学，2003.

[11]王培崇，雷凤君，钱旭.改进人工鱼群算法及其收敛性分析[J].科学技术与工程，2013，13（3）：616620.

[12]汪丽娜，陈晓宏，李粤安，等.基于人工鱼群算法和模糊C2均值聚类的洪水分类方法[J].水利学报，2009，40（6）：743755.

[13]何登旭，曲良东.一种新的混合聚类分析算法[J].计算机应用研究，2009，26（3）：879880.

（责任编辑：杜能钢）