浅谈勾股定理在初中数学教学中的应用
2017-06-20四川省仁寿县华兴中学
四川省仁寿县华兴中学 王 桃
一、引言
勾股定理是初中数学中非常重要的一个定理。它很好地解释了直角三角形中三边的数量关系,对于几何学当中有关直角三角形的计算证明问题,利用勾股定理往往能使学生快速解决问题。同时,在日常生活及工作中,勾股定理的应用也非常广泛。笔者根据多年的教学经验,利用勾股定理如何来解决“线段求长度”“面积”“最短路径”“实际问题”进行分析和探究,希望以此能够为初中数学教学提供有效依据。
二、勾股定理的应用
(一)勾股定理在三角形的高问题中的应用
在初中数学中,求三角形的高如果直接去求会非常困难,而利用勾股定理则非常轻松求出高。
1.利用勾股定理求直角三角形斜边上的高
例题1.如图,在长方形A B C D中,AD=4,CD=3,AE⊥BD,则AE等于多少?

[解析] 利用直角三角形两直角边的乘积等于斜边与斜边上的高相乘(等积法)
解:∵正方形ABCD,BC=3
∴ ∠BAD=90°,AB=3
在直角三角形ABD中
∵AD=4,AB=3
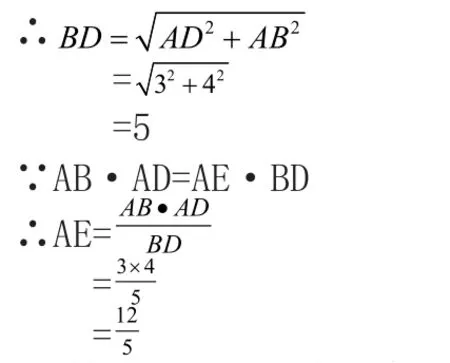
2.利用勾股定理求一般三角形一边上的高
例题2.如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?

[解析] 解决一般三角形某边上的高,常常通过勾股定理,利用三边关系列方程
解:过点A作AD⊥ BC,设BD=x,则DC=(14-x)米
∵在Rt△ABD与Rt△ACD中,由勾股定理得:
AB2-BD2=AD2=AC2-DC2
即132-x2=152-(14-x)2
解得x=5
(二)勾股定理在面积问题中的应用
例3.如图,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,则图中阴影部分面积是多少?

[解析] 解决面积问题,首先通过图形将面积问题转化为求线段的长度问题,在直角三角形中要求某条线段的长,通常设未知数,利用三边关系来列方程。
解:∵正方形ABCD,AB=8
∴AD=BC,AB=CD=8cm
∵CE=3cm
∴DE=8-3=5cm
∵将△ADE折叠到△AFE
∴AD=AF,DE=EF=5cm
在直角△CEF中
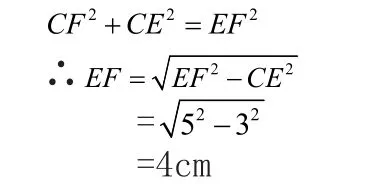
设BF=xcm,则AF=AD=(x+4)cm
在直角△ABF中

(三)勾股定理在最短路程问题中的应用
例4.如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
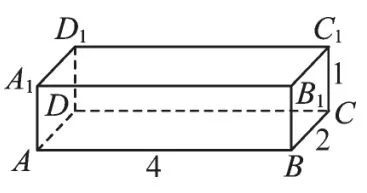
[解析] 蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式,分别展成平面图形如图:
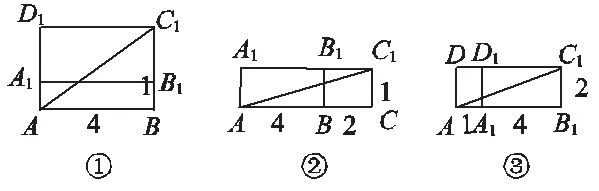
解:如图①,在Rt△ABC1中,
AC12=AB2+BC12=42+32=25,
∴AC1=
如图②,在Rt△ACC1中,
AC12=AC2+CC12=62+12=37,
∴AC1=
如图③,在Rt△AB1C1中,
AC12=AB12+B1C12=52+22=29,
∴AC1=
∵25<29<37,
∴沿图①的方式爬行路线长最短,最短的路线长为5.
(四)勾股定理在方位角问题中的应用
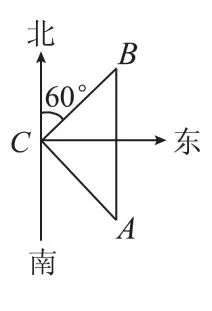
例5.如图,在C港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度前进,1小时后甲船到达B岛,乙船到达A岛,且A岛与B岛相距17海里,你能知道乙船沿哪个方向航行吗?
[解析] 对于方位角,通常是利用方位角得到直角三角形,然后利用直角三角形的三边关系,即勾股定理解决问题。
解:由题意得
AB=17,AC=5,BC=8
∵ AC2=25,BC2=64
∴ AC2+BC2=289=AB2
∴△ABC为直角三角形
∵甲沿北偏东60°
∴A沿南偏东30°
(五)勾股定理在噪音影响问题中的应用
例略。
三、总结
(一)勾股定理在初中数学中的应用一般有两条思路。
1.已知直角三角形勾股定理求第三边勾股定理逆定理。
2.已知三角形三边勾股定理逆定理得出直角三角形勾股定理。
