基于双向广度优先法的输电断面搜索方法

聂宏展，林启春，林小青

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.福州供电公司，福建 福州 350001)



基于双向广度优先法的输电断面搜索方法

聂宏展1，林启春1，林小青2

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.福州供电公司，福建 福州 350001)

为了快速、精准、完整地搜索出受潮流转移影响较大的支路组成的输电断面，采用了基于图论中改进的双向广度优先搜索算法。该方法首先以加权邻接矩阵表示电力网络，然后根据改进的双向广度优先法搜索得到开断节点间前K最短路径，通过计算路径中支路的开断分布因子选取初始输电断面，进一步计算初始输电断面的暂态稳定安全裕度筛选出关键输电断面，以此代替对全网的安全性分析，大大缩减了计算量，为后续过载控制策略争取了时间，对防止连锁过载跳闸意义重大。对IEEE39节点系统的案例仿真分析，验证了该算法的可行性和准确性。

双向广度优先搜索；前K最短路径；支路开断分布因子；暂态稳定安全裕度；关键输电断面

近几年国内外发生的大停电事故对社会造成巨大经济损失，寻其原因主要是：初始故障支路的切除导致系统发生潮流转移，使得其他正常支路可能因过载而后备保护动作，由于传统的后备保护单纯依据本地信息量变化来确定动作与否，不考虑切除故障支路对整个系统的影响，进而引发又一轮潮流转移，最终演变成连锁跳闸事故[1-5]。实际运行情况表明，在潮流转移发生之后，仅有少数支路有功潮流变化较大[6]，一般不超过系统输电线路总数的20%，而大部分支路受影响程度不大，不会出现因过载而后备保护动作的情况。快速搜索分析受潮流转移影响较大的支路组成的关键输电断面，相较于对全网的计算分析更加简便节省了时间，对防止发生连锁跳闸事故具有重要意义。

针对潮流转移后关键输电断面的搜索问题，已有学者进行了相关研究[7-10]。文献[7]采用模糊聚类方法对各线路依据功率构成进行分类，获得输电断面，此种方法计算量大，耗时长，不适合在线分析。文献[8]定义了输电断面，考虑了网络实时拓扑结构及潮流分布情况的变化建立了系统状态图，经过简单的矩阵计算，快速识别出关键输电断面，由于对系统进行分区，无法搜索区内支路。文献[9]和文献[10]分别利用动态规划原理和图论中的广度优先法，搜索开断支路首端节点到末端节点间的最短路径，但仅搜索一条路径，可能造成某些关键支路的漏选。

本文采用了一种基于双向广度优先法的输电断面搜索算法。首先通过图论相关知识将电力网络以加权邻接矩阵表示，然后利用改进的双向广度优先搜索算法结合前K最短路径，从开断支路的首端节点和末端节点同时进行扩展，直至两个扩展方向上出现相同的节点状态，形成第一条有效路径，以此类推，搜索出前K条最短路径，选取支路开断分布因子和暂态稳定安全裕度符合一定阈值的支路加入关键输电断面。本算法无需进行全网计算搜索，也无大量矩阵运算，满足实时性要求，具有重要的实际运用价值。

1 图论的相关知识

图论是数学的一个分支，图可以用来描述现实问题中某些事物间的某种特定关系。图G是由一个二元组，记为G=(V，E)，其中V={v1，v2，…，vn}，表示图G的节点集，V中的元素即为图G的节点；E={e1，e2，…，em}表示图G的弧集，E中的元素即为图G的弧[11]。设有向图G具有n个节点和m条弧，以支路电抗值表示每条弧的权重，则图G的加权邻接矩阵An*n表示如下：

(1)

式中：wij为以支路电抗值表示的每条弧的权值；∞为节点vi与vj间没有支路。

2 输电断面搜索算法

2.1 广度优先搜索算法

广度优先搜索算法是搜索图最简捷的算法之一，其搜索过程类似于树的逐层遍历[12]。遵循从图的某个顶点v0出发，在访问节点v0后，依次扩展访问v0节点有弧关联的所有未被访问的邻接点vs，并作已访问标记，再依次按vs1，vs2，…，vsl的顺序，访问与这些邻接点相关的所有未被访问的邻接点，作已访问标记，以此类推，直到所有节点均被访问为止。广度优先搜索的原理如下图所示：

图1 广度优先搜索原理图

图2 双向广度优先搜索算法原理图

2.2 双向广度优先搜索算法

双向广度优先搜索算法是对广度优先搜索算法的一种扩展[13]。广度优先算法从起始节点开始逐层扩展遍历直至遇到目标节点；而双向广度优先算法从起始节点和目标节点两个方向同时进行扩展，直到出现相同的节点状态为止，那么认为路径：起始节点—相交点—目标节点，即为所求最佳路径。双向广度优先算法相对广度优先算法来说，由于采用了两个方向拓展的方式，搜索深度得到明显减少，所以在算法的时间复杂度和空间复杂度上都有较大优势。扩展过程如图2所示，设以为vtop起始节点，vtail为目标节点进行双向广度优先搜索，得到相交节点ve，则得到路径vtop-vtp1-ve-vtl2-vtail即为起始节点vtop和目标节点vtail之间的最短路径。

2.3 改进的双向广度优先搜索算法

当初始故障支路切除后，系统发生潮流转移，由基本电路知识可知，有功功率将从断开的故障支路首端节点沿着电气距离较小的支路转移到故障支路的末端节点。双向广度优先搜索算法只能搜索出断开支路首末节点间经历最少节点数的路径，并非电气距离最短路径；且该算法只遍历出一条最短路径，而受潮流转移影响而过载的线路并非都在最短路径上。针对现有双向广度优先算法存在的不足进行相应改进：引入支路阻抗表征网络中每条弧的权，由于在高压输电网输电线路的电阻值相比于电抗值可以忽略不计，进而以搜索路径累加电抗表示电气距离；结合前K最短路径算法[14，15]，搜索出开断支路首端节点和末端节点间电气距离的第一最短路径到第K最短路径，扩大搜索范围，避免漏选。据文献[14]K值选取原则如式(2)所示，即K取不超过-1/Dmin的最大整数的绝对值，即：

(2)

式中：Dmin为支路开断分布因子阈值。

3 输电断面的选取原则

当系统中某一线路因故障开断后，其原有有功潮流将按一定比例转移到距其电气距离较近的线路上。利用改进的双向广度优先搜索算法可以快速搜索出开断支路起始节点和目标节点间电气距离较短的前K条有效路径，下一步则需从中筛选出受潮流转移影响较大且容易发生过载跳闸事故的支路加入关键输电断面中，作为后续控制策略的重点监控对象。为此本文引入支路开断分布因子和暂态稳定安全裕度来筛选出受潮流转移影响较大的关键支路集合。

3.1 支路开断分布因子

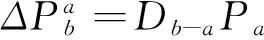
(3)

(4)

式中：Db-a为支路开断分布因子即支路a断开后，支路b的潮流增量占开断前支路a有功功率的比例；x表示支路电抗值；XB-a=MbTXMa表示端口b和端口a节点对间的互阻抗；Xa-a=MaTXMa表示端口a节点对的自阻抗；X为节点阻抗矩阵；MB、Ma分别表示支路b、支路a的变动支路关联向量。

可见开断分布因子表征了其余正常支路有功潮流变化量的大小，将支路开断分布因子满足式(5)的支路加入初始输电断面。

Db-a>Dminb∈E，

(5)

式中：Dmin为初始输电断面开断分布因子阈值，本文取0.3。

同时由式(3)便可计算出支路a断开后，支路b的有功潮流Pb.h：

(6)

式中：Pb.q、Pb.h分别为支路a开断前、后流过支路b的有功功率。

3.2 暂态稳定安全裕度

支路开断分布因子越大只能说明支路的有功潮流增量越大，并不能全面反映支路受潮流影响具体情况。在实际电力系统运行中，重载的长距离输电联络线安全裕度低往往容易出现过载，致使系统发生暂态失稳的情况[18]，是电力系统暂态稳定的重点监控区域。考虑到系统的暂态稳定安全，引入安全裕度Ysec来评价受潮流转移影响的关键输电断面，更加符合电力系统的实际运行情况。安全裕度Ysec满足式(7)的支路将被选为关键输电断面。

Ysec=1-Psec/PsTTC

(7)

式中：Psec为线路传输的有功功率；PsTTC为线路的传输有功功率极限；Ymin为线路安全裕度阈值，据实际运行人员的经验，Ymin一般取0.6，表征高压大功率传输线路功率大于极限传输容量40%的输电断面需要列为关键输电断面的监控对象。

4 基于改进双向广度优先法的输电断面搜索过程

设两个队列集合Queue1、Queue2别用于起始状态正向扩展和目的状态反向扩展，Xmin1表示正向扩展累加电抗，Xmin2表示反向扩展累加电抗，Xmin=Xmin1+Xmin2表示路径累加电抗，算法框图如图3所示。

图3 关键输电断面搜索算法框图

图4 IEEE39节点系统接线图

具体关键输电断面搜索过程如下：

第1步：输入起始节点，目的节点，令队列集合Queue1中队列队头元素为vtop=v0队列集合Queue2中队列队头元素为vtail=vs。

第2步：对Xmin1、Xmin2、Xmin均作置零处理。

第3步：判断vtop、vtail是否存在邻接节点，若存在则进入第4步，否则跳转至第13步。

第4步：vtop的邻接节点个数i是否不超过vtail的邻接节点个数j，若是执行第5步，否则执行第6步。

第5步：寻找vtop的一个邻接节点vtop.b令vtop=vtop.b且Xmin1=Xmin1+XB并作已读标记。

第6步：寻找vtail的一个邻接节点vtail.b令vtail=vtail.b且Xmin2=Xmin2+XB并作已读标记。

第7步：计算路径累加电抗Xmin=Xmin1+Xmin2。

第8步：判断队列集合Queue1、Queue2中的队列是否含有相同元素称为相交节点，若是则执行第9步，否则返回第3步。

第9步：将扩展路径“起始节点—相交节点—目的节点”存入有效路径集合S中，并根据其路径累加电抗由小到大进行排序，取前K条路径。

第10步：计算集合S中各支路的支路开断分布因子，将计算结果满足式(5)的支路加入初始输电断面集合S1中。

第11步：计算初始输电断面集合S1中支路的暂态稳定安全裕度，将计算结果满足式(7)的支路加入关键输电断面集合S2中。

第12步：输出关键输电断面集合S2。

第13步：结束。

5 算例分析

为验证本算法的准确性和可行性，使用Matlab对IEEE39节点系统进行仿真计算分析，其网络接线图如图4所示。

作为比较对象，假设系统中支路10-支路13开断，文献[9]根据动态规划原理的分支界限算法确定开断支路首端节点和末端节点间的最短路径，计算最短路径包含支路的开断分布因子，认为超过阈值(根据运行人员经验，本文取0.3)的支路即为可能引发连锁跳闸事故的关键支路，结果如表1所示。

同样以支路10-13支路因故障切除为例，本文算法首先以10节点为起始节点，13节点为目的节点对系统进行双向广度优先搜索，得到10节点和13节点间的K条有效搜索路径，并根据路径累加电抗大小进行排序，由式(2)计算可得K=4，搜索路径结果见表2。根据输电断面的选取原则，选取结果如表3所示。

表1 基于分支界限算法的输电断面搜索结果

表2 基于双向广度优先法搜索前K最短路径结果

表3 输电断面选取结果

由表1结果可知，该搜索算法只搜索出了开断支路首末端节点间的一条最短路径，最后只得到支路10-支路11、支路11-支路12两条关键路径。由于受潮流转移影响较大的支路未必都在最短路径上，故而文献[9]的方法会造成了部分重要输电断面的漏选。根据表2 结果，支路10-11、6-11、5-4、5-6、12-11的开断分布因子均超过了阈值，表示受潮流转移影响支路的潮流增量较大，经计算其中支路10-11、6-11、5-4、5-6暂态稳定安全裕度较小，表示支路传输潮流接近支路潮流极限，容易引发过载而导致新一轮潮流转移，需加入关键支路重点监控对象。

同时由对支路开断后系统进行潮流计算结果可知，支路10-11、6-11出现过载，文献[9]搜索的关键输电断面结果中不包含支路6-11，证明了其搜索算法存在漏选缺陷，而本文搜索出的关键输电断面中包含了支路10-11和支路6-11，验证了本文搜索算法的可行性和搜索结果的完整性、准确性。

6 结 论

本文总结了连锁过载跳闸事故的原因并提出了基于改进双向广度优先法的输电断面搜索新方法。本方法将广度优先搜索算法推广到了双向广度优先搜索算法，减少了搜索深度，并对双向广度优先搜索算法做出了改进，引入支路累加电抗来表示搜索电气距离，结合前K最短路径扩大了搜索范围，避免输电断面漏选的情况。利用支路开断分布因子和暂态稳定安全裕度共同评价关键输电断面，既考虑了开断支路对其他支路转移潮流变化量的大小，又考虑了系统暂态稳定安全因素，保证了结果的准确性。通过分析关键支路来代替对全网络的安全性分析，为后续对因潮流转移而过载的支路实施减载控制策略大大降低了难度，对防止发生连锁过载跳闸事故具有重要实际意义。

[1] 薛禹胜.综合防御由偶然故障演化为电力灾难——北美“8·14”大停电的警示[J].电力系统自动化，2003，27(18)：1-5，37.

[2] 印永华，郭剑波，赵建军，等.美加“8.14”大停电事故初步分析以及应吸取的教训[J].电网技术，2003，27(10)：8-11，16.

[3] 刘迎迎，孙毅，李昕，等.电力系统电压稳定分析方法综述[J].东北电力大学学报，2013，33 (5)：43-46.

[4] 闫常友，周孝信，康建东，等.潮流转移灵敏度以及安全评估指标研究[J].中国电机工程学报，2010，30(19)：7-13.

[5] 聂宏展，王叫，马方明，等.基于潮流转移识别的紧急减载控制策略研究[J].东北电力大学学报，2016，36(4)：1-6.

[6] 徐岩，吕彬，林旭涛.潮流转移识别方法的研究与分析[J].电网技术，2013，37(2)：411-416.

[7] 林济铿，杨添剀，胡世俊，等.基于模糊聚类和最短路径的关键输电断面确定新方法[J].电力系统自动化，2015，39(5)：134-141.

[8] 周德才，张保会，姚峰，等.基于图论的输电断面快速搜索[J].中国电机工程学报，2006，26(12)：32-38.

[9] 倪宏坤，徐玉琴.基于动态规划原理分支界限算法的关键输电断面搜索方法[J].华北电力大学学报：自然科学版，2009，36(4)：11-15.

[10] 熊俊，肖先勇，邓武军，等.基于广度优先搜索算法和区域节点行向量法的复杂配电网络可靠性评估[J].电网技术，2007，31(9)：27-32.

[11] 陈晓玲，杨军，罗超，等.一种大电网潮流转移路径快速搜索方法[J].电网技术，2015，39(4)：1045-1052.

[12] 匡桂娟.广度优先搜索算法在互连网络通信中的应用[D].青岛：青岛大学，2005.

[13] 王桂平，张帅.基于双向广度优先搜索的魔力方块问题求解[J].计算机工程，2011，37(20)：219-222.

[14] 王增平，李刚，任建文.基于前K最短路径的输电断面搜索新算法[J].电工技术学报，2012，27(4)：193-201.

[15] S.A.Paluch.Multilable algorithm for K shortest paths problem [J].Komunikacie，2009，11(3)：11-14.

[16] 张富超，钟成元，张富春，等.基于源流路径剖分的输电断面快速搜索[J].电力系统保护与控制，2015，43(12)：8-13.

[17] 聂宏展，袁晓丹，张会强，等.基于多支路开断和关键支路集的快速潮流转移识别[J].电力系统保护与控制，2014，42(17)：38-43.

[18] 赵峰，孙宏斌，谭嫣，等.综合考虑多种电网安全主题的关键断面自动发现方法[J].电网技术，2014，38(5)：1169-1174.

The Search Method of Transmission Section Based on Double Breadth First Algorithm

Nie Hongzhan1，Lin Qichun1，Lin Xiaoqing2

(1.Electrical Engineering College，Northeast Electric Power University，Jilin Jilin 132012；2.Fuzhou Power Supply Company，Fuzhou Fujian 350001)

In order to search transmission section consisting of the branches that influenced greatly by flow transferring rapidly，accurately，completely，this paper presents an improved double breadth first search algorithm based on graph theory.In the proposed algorithm，firstly，the power network is expressed as weighted adjacency matrix；secondly，theKshortest paths between the breaking nodes are searched，according to the improved double breadth first search method.The initial transmission section is selected by calculation of line tripping distribution factors，and then calculate transient stability safety margin of the initial transmission section to select the key transmission section，replacing security analysis of the entire network which reduces the amount of calculation greatly and gains time for subsequent overload control strategy.It is significant to prevent cascade overload trips.Simulation results of IEEE 39-bus system show that the proposed algorithm is accurate and feasible.

Double breadth first search；TheKshortest paths；Line tripping distribution factors；Transient stability safety margin；The key transmission section

2017-03-12

聂宏展(1962-)，男，硕士，教授，主要研究方向：电力系统规划、电力系统继电保护.

1005-2992(2017)03-0013-06

TM715

A

电子邮箱： niehz@nedu.edu.cn(聂宏展)；847779855@qq.com(林启春)；124222794@qq.com(林小青)