对“乘法分配律”的教学研究
2017-06-19张涛兴
张涛兴

一、问题
乘法分配律在《义务教育数学课程标准(2011年版)》中叫做乘法对加法的分配律。关于乘法分配律的“分配”的理解,我们认为,分配应不作为一个完整的词而将其分开为“分”与“配”,“分”即为分开,“配”即为结合。这样理解容易把握其含义。
与其他运算律相比,乘法分配律是运算定律教学中的难点。一是它涉及两种运算,既有加法,又有乘法,学生初学时对其特征较难把握,对一些相似的式子如a×b+a+c,a+b×a+c等常会误套用。二是它有两个表达式:(a+b)×c=a×c+b×c,a×(b+c)=a×b+a×c。在表述上需要将“两个数的和乘一个数”与“一个数乘两个数的和”概括为“两个数的和与一个数相乘”,增加了概括的难度。三是文字表述涉及较多的概念。如“两个数的和”、“分别相乘”,学生难于独立完成抽象概括。
二、教前思考
(一)目标与任务分析
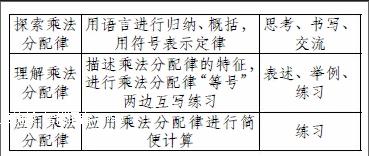
课标关于这部分内容的要求为“探索和了解运算定律,能运用运算定律进行一些简便运算”。人教版《教师教学用书》关于本节课教学目标为“探索和理解乘法分配律,能运用运算定律进行一些简便运算”。“探索乘法分配律”即要求学生参与特定的数学活动,发现乘法分配律。“理解乘法分配律”即能描述乘法分配律的特征和由来,阐述乘法分配律与其他运算律的联系与区别。为此,在教学中应完成以下相应的任务:(1)探索乘法分配律。包括以下方面:从实际问题的中发现有关例证,即解决有些问题可以用形如(a+b)×c的算式来算,也可以用形如a×c+b×c的算式来算。在此基础上提出猜想:(a+b)×c=a×c+b×c;验证猜想。通过若干具体算式计算或说理验证(a+b)×c与a×c+b×c相等;引导学生用文字进行归纳,并尝试用字母或其它符号表示。(2)理解乘法分配律。从理解结构特点入手,进行形式化练习,把握乘法分配律的内涵。(3)应用运算定律进行简便计算。
(二)设计思考
1.设计策略
一是重视利用乘法的意义理解乘法的分配律。注重通过图示而不是通过计算判断算式的结果是否相等。二是通过较为充分的例证,特别是要让学生能否提供反例。从中让学生感受用不完全归纳法得出结论时要注意的问题。
2.设计思路
根据以上认识,本课关于学习目标、学习任务、学习活动与方式的设计如下:
三、教学实践
【活动一】创设情境,体会“乘法分配律”在生活中的意义。
(投影出示植树活动情景图)
师:你能解决下面3个问题吗?
投影出示:
问题1:负责挖坑、种树的一共有多少人?
问题2:负责抬水、浇树的一共有多少人?
问题3:一共有多少名同学参加了这次植树活动?
学生解答完后,让学生说说问题3的思路。
生1:根据先算出每个小组人数,在算总人数,列式得:(4+2)×25。
生2:根据先分别计算干不同活的学生人数,再算总人数,列式得:4×25+2×25。
师:比较(4+2)×25和4×25+2×25有什么关系?
生:相等。
师:你是怎么知道的?
生:结果相等。
师:不计算,你能很快地知道它们相等吗?
生:(4+2)×25表示(4+2)个25,4×25+2×25表示4个25加2个25,它们都表示6个25,所以相等。
【活动二】举例,理解“乘法分配律”的本质。
師:你能举出像这样的例子吗?
生1:(3+2)×30=3×30+2×30
生2:(5+6)×36=5×36+6×36
师:不计算,你是怎么知道等式是成立的?
生1:3+2=5,左边式子表示5个30,右边式子表示3个30+2个30,也表示5个30。
师:也就是说把5个30分成了3个30和2个30。
师:这样的例子还有吗?有几个?
生:有无数个。
师:老师也举一个例子:25×(4+2)○25×4+25×2,相等吗?
生:相等。
师:你是怎么想的?
生1:结果相等。
生2:两边式子都可以表示6个25。
生3:把25个6分成了25个4和25个2。
师:你能举出像这样的例子吗?
生:20×(4+6)=20×4+20×6
师:不计算,你是怎么知道这两个式子是相等的?
生:把20个10分成了20个4和20个6。
师:这样的例子能写出几个?
生:无数个。
师:老师也举两个,你们判断一下相等吗?10×(2×3)○10×2+10×3,
8×(2+3)○8×2+8
生:不相等。
师:你是怎么想的?
生1:10×(2×3)表示6个10,10×2+10×3表示5个10,所以不相等。应该把10×(2×3)改成10×(2+3)。
生2:8×(2+3)表示5个8,8×2+8表示2个8+1个8,一共3个8,所以不相等。应该在8×2+8后添×3。
【活动三】比较、归纳、概括“乘法分配律”。
师:请观察等式左边的式子的运算顺序有什么共同地方?
生:先算加法,再算乘法。
师:对,先算两个数的和,再与另一个数相乘,这个数可以放在右边相乘,也可以放在左边相乘。
(师板书:和、相乘)
师:等号右边的式子的运算顺序有什么共同地方?
生:先两边相乘,再相加。
师:左右两个式子有什么关系?
生1:左右两个式子相等。
生2:把左边式子括号里的两个数分别相乘,再相加,就得到了右边的式子。
(师板书:分别相乘,再相加)
师:你能用自己的话说说什么叫做乘法分配律?
生:两个数的和与其中一个数相乘,可以先把它们与这个数分别相乘,再相加。
师:有什么办法表示乘法分配律?
生1:(a+b)×c=a×c+b×c
生2:(○+△)×□=○×□+△×□
生3:…
四、讨论
1.加强对运算定律本质与思考
如何从源头加强学生对乘法分配律本质的理解,本节课从生活情境着手,使学生领悟概念的本质,这是实现有效教学的根本。
(1)创设情境,从生活到数学。创设情境不仅可以激发学生探究兴趣,还可以引出算式,更是学生理解和思考的依托。如在本节课教学设计上教师注重了从学生的植树情境的实际出发,把数学知识和实际生活紧密联系起来,让学生在不断的感悟和体验中学习知识。
(2)经历数学活动,从表象到本质。数学活动是学生经历数学化过程的再创造活动,是学生自己建构数学知识的活动。本节课的数学活动中,让学生用两种不同的方法解决实际问题,在两个不同的算式之间建立起聯系,让学生初步感知乘法分配律。之后,给学生提供体验感悟的空间,让学生写出符合规律的式子,引导学生在研究讨论中,进一步形成清晰的表象。在此基础上,让学生自己再写出一些符合乘法分配律的等式例子,既为概括乘法分配律提供更丰富的素材,又加深了学生对乘法分配律本质的认识。
2.进一步思考的问题
用怎样合适的教学方式改进学生的理解水平呢?本节课的教学方式是:注重引导学生在课前“先学”,变教学生“学会”为指导学生“先学”,课中采用小组合作的数学活动形式教学,在小组自主探索的数学活动中,引导学生理解乘法分配律的内涵、意义和形式,从而感悟和发现乘法分配律。
总之,在整节课中,学生亲历观察、小组合作、归纳、举例、验证等探究发现的全过程,学生不仅发现乘法分配律的知识,而且学习到了科学探究的方法,数学思维能力得到了发展。
