基于EGARCH模型的云南省生产者价格指数（PPI）分析

赵芊芊　麦杨　丁巍

【摘 要】 本文利用2001年至2016年云南省生产者价格指数（PPI）的月度数据，实证说明了云南省生产者价格指数（PPI）存在ARCH效应，并建立EGARCH模型，很好拟合了云南省生产物价指数（PPI）数据，分析了其在不同冲击下的波动状况，并据此提出了政策性建议。

【关键词】 PPI EGARCH 杠杆效应

一、研究背景

生产者价格指数（PPI）主要用来衡量工业产品出厂价格的变动，是通货膨胀的三大指标之一。一直以来，国内外通常都是使用消费者价格指数（CPI）来衡量通货膨胀的变动，许多学者利用ARCH类模型对消费者价格指数（CPI）进行建模，以分析通货膨胀率的波动状况。但是，也有众多学者认为生产者价格指数（PPI）作为生产领域内价格变动的指标，一定程度上带动了消费者价格指数（CPI）的变动，可以作为通货膨胀的先行指标，在此基础上，分析生产者价格指数（PPI）的波动情况对分析与预估生产者消费指数（CPI）的走势有着重要意义。本文利用云南省生产者价格指数（PPI）数据，采用EARCH模型，对云南省2001年至2016年的生产者价格指数（PPI）波动进行分析。

二、理论模型介绍

自1982年，Engle首次提出了ARCH（auto-regressive conditional heteroskedasticity）模型，使用此模型针对英国的通货膨胀率作出分析，而后ARCH类模型得到了很大的发展，1986年Bollerslev 扩展了Engle 的原始模型，引入了一种允许条件方差转化为一个ARMA过程的方法，提出了GARCH模型；1987年Engle，Lilien和Robin将基本的ARCH模型加以扩展，提出了ARCH-M模型，反映了将风险因素引入金融资产定价过程的思想；由于GARCH模型广泛的应用性，围绕着GARCH模型，众多的拓展模型被开发出来，包括非对称的TGARCH模型和 EGARCH模型，能够更好的分析具有杠杆效应的经济金融时间序列。

本文为研究云南省生产者价格指数（PPI）的波动及其杠杆效应，采用EGARCH模型，其理论模型如下：

若βk≠0，说明了冲击对研究对象非对称的影响，即存在着杠杆效应，负冲击相比于正冲击所带来的波动大小不同。

三、实证分析

（一）数据选取

本文选取2001-2016年共192个月度云南省生产者价格指数（PPI）数据，数据来源于国家统计局网站。本文所有模型均在Eviews 6.0中实现。

（二）平穩性检验

经济时间序列的平稳性检验必不可少，因此，首先对生产者价格指数（PPI）时间序列进行平稳性检验，平稳性检验包含多种方法，因为DF检验要求时间序列不存在自相关性，而大多数经济时间序列不满足此项假设，因此这里采用ADF检验，得到如下结果。

表1：生产者价格指数（PPI）的单位根（ADF）检验

Null Hypothesis： PPI has a unit root

t-Statistic Prob.*

ADF statistic -3.706337 0.0047

Test critical values： 1%level -3.465202

5%level -2.876759

10%level -2.574962

由上表可知，分别在1%，5%，10%的置信水平下，t统计量绝对值均大于临界值，因此拒绝该序列存在单位根的原假设，生产者价格指数（PPI）序列平稳。

（三）均值方程和残差序列

由于生产者价格指数（PPI）序列平稳，所以选择用自回归模型解释生产者价格指数（PPI）的变化，对生产者价格指数（PPI）序列做自相关检验，确定其滞后阶数为1阶，采用如下公式做其均值方程：

PPIt=θ0+θ1PPIt-1+εt

按该均值方程，使用OLS方法进行估计，得到相应的残差序列，绘制平方残差序列与时间变化的关系图，如下图所示，可以观察到平方残差在随时间变化的过程中存在聚类现象，这意味着ARCH效应的存在。

（四）ARCH-LM检验

为进一步确定残差序列ARCH效应的存在，要进行更为正式的LM检验，其检验结果如上表所示，此处P值等于0，拒绝原假设，说明AR（1）模型的残差序列存在自回归条件异方差，进一步证明了εt存在着显著的ARCH效应，且可以在AR（1）模型的基础上建立EGARCH模型。

（五）EGARCH模型及其结果分析

依据AIC和SC最小的原则，对不同分布下的模型进行比较，认为正态分布下的模型拟合效果最好，模型回归结果可表示为：

均值方程：

方差方程：

对数似然值=-305.180 AIC=3.258

SC=3.361

在EGARCH模型中，α的估计值为0.717，非对称项γ的估计值为-0.171。当μt-1>0时，该信息冲击对条件方差的对数有一个 0.717+（-0.171）=0.546倍的冲击；μt-1<0时，它给条件方差的对数带来的冲击大小为 0.717+（-0.171）×（-1）=0.888倍，即说明生产者价格指数（PPI）的波动具有杠杆效应，负的信息冲击比正的信息冲击对生产者价格指数（PPI）带来的波动更大。

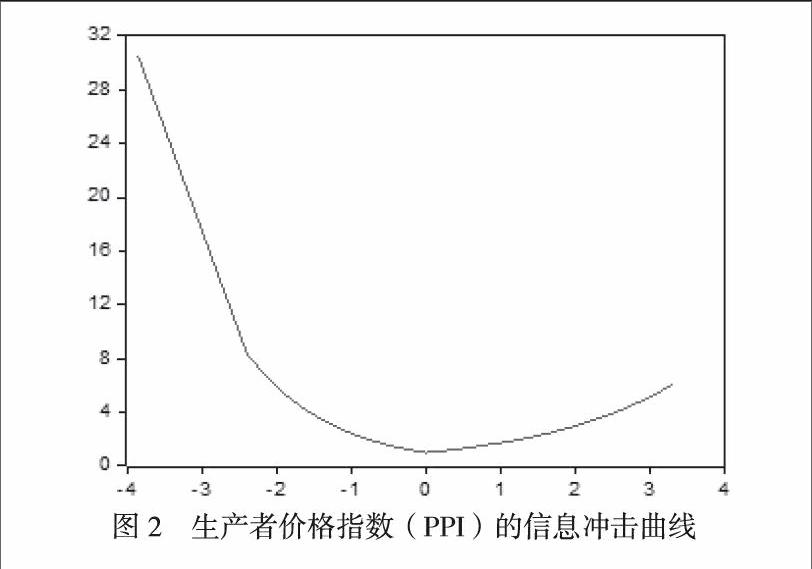
（六）信息冲击曲线

根据EGARCH模型的结果，可以绘制出相应的信息曲线，进一步说明生产者价格指数（PPI）的波动具有的非对称性，从上图可以看出，这条曲线在信息冲击大于0时，即代表着正冲击时，比较平缓，而在负冲击时比较陡峭，说明了负的冲击相比正冲击对生产者价格指数（PPI）带来的波动性变化更大一些。

（七）模型预测

在上述EGARCH模型的基础上，对生产者价格指数（PPI）进行模型预测，发现2016年7月实际值为97.80，预测值为97.15，相对误差为0.66%，2016年7月实际值为98.80，预测值为97.84，相对误差为0.97%，2016年7月实际值为99.50，预测值为98.81，相对误差为0.69%，2016年7月实际值为100.4，预测值为99.50，相对误差为0.90%，2016年7月实际值为102.6，预测值为100.38，相对误差为2.16%，2016年7月实际值为104.2，预测值为102.53，相对误差为1.60%，以上六组预测中，预测数据非常接近实际数据，且有4组预测的相对误差小于1%，因此可以相信EGARCH模型的预测效果很好，可以用做短期的预测。

四、结论

（一）本文通過生产者价格指数（PPI）的自相关性检验，可以看出生产者价格指数（PPI）与其滞后一项相关性较强，建立生产者价格指数（PPI）的一阶自回归模型，并对该方程的残差平方做随时间变化的关系图，可以看出生产者物价指数波动的集群性，发现了ARCH效应的存在，并且通过ARCH-LM检验证实了这一点，为研究生产者价格指数（PPI）波动的杠杆效应，建立了EGARCH模型，很好的说明了生产者物价指数在波动过程中的非对称性，并且绘制出信息冲击曲线，更加形象的解释了生产者价格指数（PPI）受信息冲击的波动情况，最后在EGARCH基础上对生产者价格指数（PPI）进行了样本内的预测，发现EGARCH模型的预测效果良好。

（二）根据实证分析，可以看出生产者价格指数（PPI）的波动具有明显的杠杆效应，负的冲击对其波动有更加强烈的影响，即生产者价格指数（PPI）的上升会带来其更加剧烈的波动，下降时波动则会变小，由于生产者价格指数（PPI）对消费者价格指数（CPI）具有一定的前瞻性，因此生产者价格指数（PPI）波动一段时期后，通货膨胀也会发生相应的波动。生产者价格指数（PPI）明显的杠杆效应证明了云南省的市场经济还不具备完备的自我稳定能力，因此政府要加强对价格的干预，以维持价格系统的平稳运行。

【参考文献】

[1] 高铁梅.计量经济分析方法与建模[M].清华大学出版社.2009年第二版

[2] 张雪莹 金德环. 金融计量学教程[M].上海财经大学出版社.2005年第一版

[3] 孙朗成.基于EGARCH模型的我国通货膨胀率预测[J].沿海企业与科技.2009年第7期

[4] 万春林 何慧杰.基于ARCH模型的我国生产者物价指数（PPI）研究[J].经济论丛

[5] 伍旭.PPI：当前我国通货膨胀的先行指标——基于PPI引导CPI变动的研究[D].暨南大学

[6] 蒋成林 蒋汶秀.基于ARCH类模型的我国通货膨胀波动率分析[J].统计与决策.2013年第8期

作者简介：赵芊芊，（1994- ）陕西宝鸡人，硕士研究生，主要研究方向数量经济学；麦杨，（1994- ）云南玉溪人，硕士研究生，主要研究方向金融学；丁巍，（1990- ）河南商丘人，硕士研究生，主要研究方向金融学。