岩溶隧道含水裂缝扩展规律研究

张志成，唐德高，戎晓力，黄厚旭

(解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007)

岩溶隧道含水裂缝扩展规律研究

张志成，唐德高，戎晓力，黄厚旭

(解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007)

为了探索岩溶隧道在施工过程中经常出现由于裂缝引发突水的灾害机理，利用水压致裂原理重点分析研究拉剪破坏突水和压剪破坏突水的力学过程和裂缝扩展过程中缝内水压分布特征和梯度。研究表明：突水临界水压受裂缝的走向、所处位置等因素的影响；含水裂缝发生拉剪破坏所需的临界水压力大于其发生压剪破坏所需的临界水压力；在水力劈裂作用下裂缝的生长呈现间断性特征。研究成果对隧道施工过程中突水灾害的防治具有重要的意义。

岩溶隧道；含水裂缝；突水灾害；拉剪破坏；压剪破坏；缝内水压；间歇性

1 研究背景

岩溶隧道施工过程中经常出现突水突泥灾害，突水突泥不仅严重威胁工程安全而且破坏当地的生态环境。一旦大规模的突水发生，抽、排水几乎成为其唯一的治理措施，这将严重浪费财力物力。岩溶隧道超前地质预报[1]是进行岩溶隧道突水突泥防治的重要措施，而了解含水裂缝的破坏机理以及生长过程中内部水压的分布对于有目的性地进行地质预报具有重要意义。

岩溶隧道围岩所含裂缝与干燥岩石中所含裂缝最大的差别在于前者所含裂缝中有水，因此有必要了解缝内水压对裂缝生长造成的影响，也即含水裂缝的破坏模式。裂缝的生长过程也是缝内水压不断变化的过程，了解缝内水压的变化特征有助于把握裂缝的破坏趋势。水压致裂是水岩之间典型的作用形式，国内外在相关方面的研究取得显著成果，比如孙谋等[2]基于数值模拟研究了岩溶地区的长大深隧道的突水问题，并且建立隧道掌子面失稳突变模型；PESENDORFER M等[3]利用地下勘探技术测试了裂缝和岩溶洞库中的水文工程地质参数；盛金昌等[4]研究了高水压作用下的水力劈裂问题，并且将理论应用在水利水电隧道的水利劈裂风险分析中；王建秀等[5]建立了石灰岩损伤演化的断裂力学模型及耦合方程；徐栋栋等[6]也用数值计算手段分析了水电式隧道的突水问题；黄润秋等[7]基于水力劈裂相关理论对隧道涌水过程的特征及规律进行了分析；王瑜等[8]、邵磊等[9]针对岩石中裂缝的特征及扩展规律都展开了研究。水压致裂影响着人们对于含水裂缝破坏模式的认识，认为含水裂缝是由于水力劈裂而导致不断扩张生长，裂缝的生长又导致水流通道不断扩大、突水量随之增加，最后导致了大规模突水的形成，正是因为这看似合理的过程影响了人们对含水裂缝内部水压变化与裂缝扩展的认识。为了弄清含水裂缝扩展与缝内水压变化的关系，本文建立了含水裂缝模型，分析了裂缝扩展的主要模式，并对裂缝扩展过程中内部水压的变化进行了分析。

2 裂缝中水压对裂缝的不利影响分析

通过隧道施工现场的观测表明，掌子面突水往往存在一个从量小到量大的非连续变化过程，爆破以及作业机械的扰动使围岩内原生裂缝激活扩展并产生大量次生裂缝，由于岩溶岩体中富含水体，所以胀开的裂缝中极易充水，如果将裂缝视为扁椭圆，那么根据裂缝破坏方向和沿长轴或短轴至少可以把裂缝的破坏方式划分为2种：①当裂缝沿短轴扩张，裂缝开度不断增大，使其储水能力不断加强时，这种破坏可以成为裂缝的拉剪破坏；②当裂缝内充水，但由于裂缝周围压力变化的原因导致裂缝含水，但开度几乎不变，接着裂缝沿长轴滑移破坏，此时的破坏可归结为压剪破坏。这也是本文将要重点研究的2种情况，而在以上2种情况中，裂缝水体所起的作用也各不相同，裂缝水体最主要的是对裂缝内壁提供径向正应力σw。当裂缝拉张破坏时，该径向应力用于撑开和撕裂裂缝，而当压剪破坏出现时，该径向应力用于提供-σtanφ，根据摩尔库伦准则可知这有利于减小压剪破坏过程中裂缝内面岩壁之间的摩阻力，加剧压剪破坏的发生，直观上看此时的水体可看作是分布于裂缝内的润滑剂。从以上的分析可知，无论是拉剪破坏还是压剪破坏，裂缝内部水压都起到了重要的作用并存在一个导致相应破坏发生的临界水压——拉剪破坏临界水压力和压剪破坏临界水压力。以下将建立相应模型对这2种破坏方式进行计算分析，并确定含水裂缝破坏的主要方式。

2.1 临界水压力的确定

隧道掘进过程中掌子面和隧道侧壁面上裂缝的方向、大小和分布种类非常繁多。为了简化分析，本文只分析在掌子面和隧道侧壁面面内扩张并能贯通岩体的这类裂缝。由于只分析裂缝的扩张效应不分析裂缝贯通掌子面的过程，而扩张效应可认为是发生在一个面内，因此可将问题简化为二维平面问题。图1为岩溶隧道所受地应力和隧道掌子面及侧壁面上含水裂缝单元的受力图示，而图2中的(a)和(b)分别是岩溶隧道掌子面和两帮面上的含水裂缝的详细受力分析图，结合工程实际，可认为处于直墙拱隧道两帮上含水裂缝单元的受力情况与位于隧道前方掌子面上含水裂缝的受力情况是相似的。

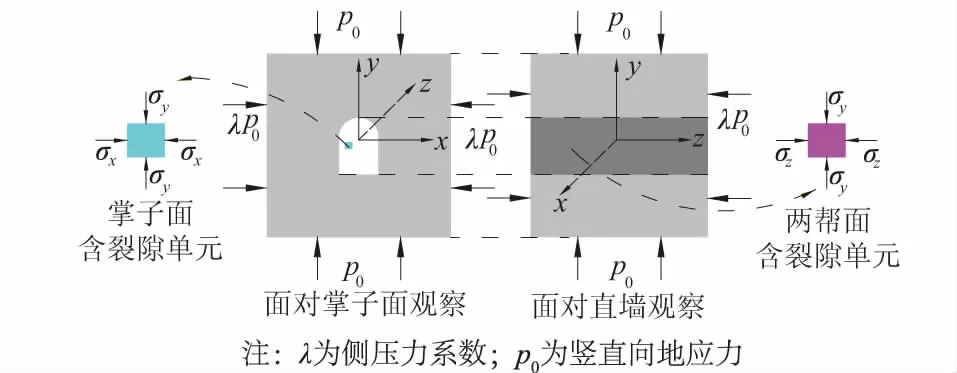
图1 开挖隧道掌子面和两帮面含裂缝单元受力情况Fig.1 Load-bearing conditions of water-bearing fractureunits on tunnel excavation face and both sides

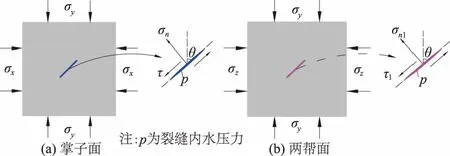
图2 掌子面和两帮面上的充水裂缝受力情况Fig.2 Force analysis of water-bearing fractures ontunnel excavation face and both sides

2.1.1 拉剪破坏突水

根据断裂力学理论，在远处应力σx和σy共同作用下，岩溶隧道岩体裂缝可以简化为扁椭圆形裂缝模型，σy与裂缝的夹角为θ，裂缝上各处的应力状态可以表示为

(1)

式中σn和τ为裂缝法向和切向应力。

(2)

由拉剪破坏准则可得

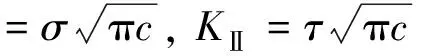
(3)

式中：KⅠcc为Ⅰ型断裂韧度值；KⅠ和K分别为Ⅰ型和Ⅱ型应力强度因子；c为裂缝长度。

联立式(1)、式(2)和式(3)可以得岩溶隧道岩体发生拉剪破坏的临界水压为

(4)

2.1.2 压剪破坏突水

当充水裂缝岩体发生压剪破坏时，裂缝压的存在减小了裂缝间的摩阻力，裂缝的有效剪应力为

(5)

由式(1)、式(2)、式(5)可得

(6)

同时压剪破坏的断裂准则为

(7)

联立式(5)、式(6)、式(7)可得压剪破坏临界水压为

(8)

由式(4)和式(8)可以看出，含水裂缝发生拉剪破坏和压剪破坏的临界水压受竖直地应力p0、岩石内摩擦角φ0、裂缝走向θ、裂缝半长c和侧压力系数λ的共同影响。

2.2 临界水压力的影响因素分析

2.2.1 裂缝破坏受侧压力的影响分析

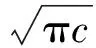
(9)

(10)

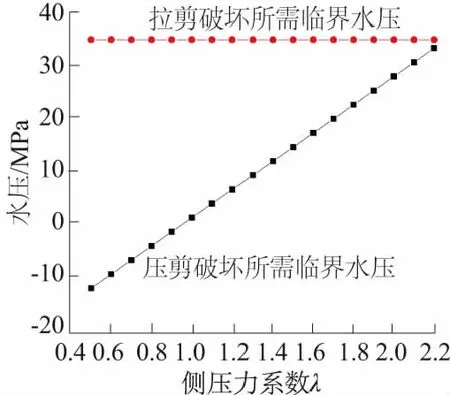
图3 掌子面上裂缝破坏受侧压力影响Fig.3 Failure of cracks ontunnel face affected by lateralpressure

从图3可以看出，在其他条件限定的情况下，掌子面上裂缝发生压剪破坏所需的临界水压应力将会随着侧压力系数的增大而线性增长，但在可接受的侧压力范围内，压剪破坏所需的临界水压应力小于水力劈裂所需的临界应力。

2.2.2 裂缝破坏受裂缝长度的影响分析

当含水裂缝在隧道掌子面上时，取侧压力系数λ=1、取裂纹长轴与竖向之间的夹角θ=π/4时，根据以上条件则式(4)和式(8)可分别化简为：

(11)

(12)

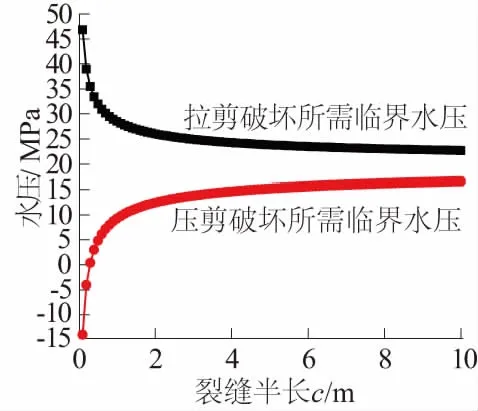
图4 掌子面上裂缝破坏受裂缝长度影响Fig.4 Failure of crackson tunnel face affected bylength of cracks

从图4可以看出，在裂缝长度逐渐增长的过程中，拉剪破坏所需的临界应力减小而压剪破坏所需的临界应力增大，这可能是由于裂缝长度增大导致裂缝间滑动时潜在的接触面积增大，使得需要更大的水压应力支撑裂缝相互滑动的面才能使压剪错动更易实现。且当裂缝半长度<1.5m时，随着裂缝长度的增长，发生2种临界破坏的水压应力将随着裂缝长度的增长而变化明显；当裂缝长度>1.5m时，裂缝半长度的变化对裂缝发生2种破坏所需的临界水压应力的影响减小，并且同样亦可得出发生拉剪破坏所需的临界应力大于发生压剪破坏所需的临界应力。

2.2.3 裂缝破坏受裂缝走向的影响分析

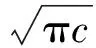
(13)

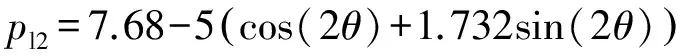
(14)

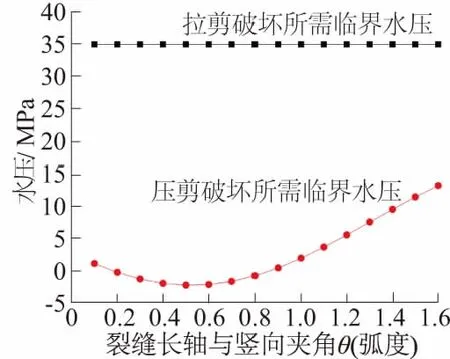
图5 掌子面上裂缝破坏受裂缝走向影响Fig.5 Failure of crackson tunnel face affected bytrend of cracks

从图5可以看出，受裂缝与竖向应力之间夹角的影响(考虑到对称性，此处仅取到π/2弧度即可)，裂缝发生压剪破坏所需的临界应力发生波动，但整体上随着裂缝与竖向之间夹角的变化而变大，同样亦可得出，裂缝发生压剪破坏的临界水压应力小于裂缝发生水力拉剪破坏所需的临界应力。

3 裂缝扩展过程中缝内水压分布分析

裂缝的生长将伴随着缝内水压的变化，而缝内水压的变化又将反过来影响裂缝的生长。为了分析裂缝生长过程中内部水压的变化，假设裂缝形状为扁椭圆，裂缝的生长方式有3种：仅沿长轴方向增长(长度变化)；仅沿短轴方向扩张(开度变化)；同时假设沿长轴方向增长和沿短轴方向扩张。同时初始时刻裂缝内部充水，缝内水压稳定，水体的黏性不可忽略，水流为稳定层流。

在裂缝生长的瞬间，缝内水流所受阻力较大，缝内水体所受自然压力恒定，因此裂缝内部新增长的空间很可能来不及被水填充，也就是说在裂缝扩展瞬间的某一时段t内裂缝内水体质量m不变，即

(15)

假设裂缝长轴沿水平方向，根据椭圆方程有

(16)

式中c和b分别为长轴和短轴长度的一半。

根据流体力学原理，考虑流体的黏阻和层流效应，流体内任一点的水流速度可表示为

(17)

式(17)在平面内表示以x轴为对称轴的抛物线，其意义是越靠近边界，流速越小，这是边界黏滞阻力作用的结果。

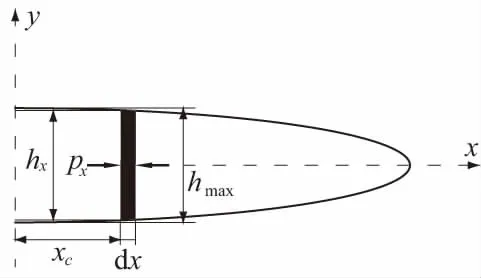
图6 扁椭圆裂缝断面模型Fig.6 Elliptical cross-section model of cracks

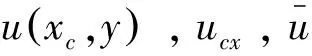
(18)

流体微元的截面可近似看作梯形，其体积近似为

(19)

忽略流体体积力，考虑流体单元受到的边界摩阻剪力f=2τ，根据牛顿剪力公式，有

(20)

根据平均流速的定义可推出流体微元左右两断面处的平均流速为

(21)

对于层流，断面的最大流速为其平均流速的2倍，即

(22)

将式(17)代入式(20)并用插值法求得流体微元中间断面的最大流速和高后可得摩阻剪力为

(23)

考虑到流体微元厚度dx→0，此处可认为ucx=udx，hx=hx+，将式(21)、式(22)代入式(23)，最终可得摩阻剪力为

(24)

则流体微元受到的沿x方向的合力为

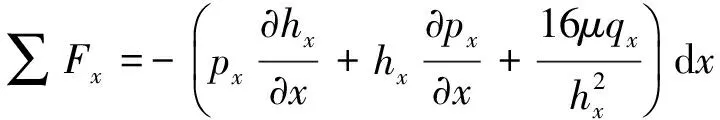
(25)

(26)

将式(26)两端同时点乘速度矢量U可得不可压缩流体的动量守恒关系式为

(27)

式中：U为速度矢量；P为动量；n为面积微元dA方法向量。

根据平面层流特点和式(20)、式(21)、式(22)以及以上假设可得

(28)

将式(18)、式(28)代入式(26)可得裂缝中流体质量守恒的最终形式，即

(29)

同理，可对动量守恒关系可作如下变换：

(30)

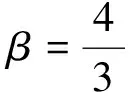
(31)

(32)

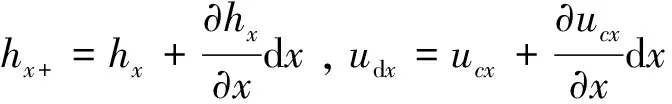
(33)

(34)

式中Fx为流体微元受到沿x方向的合力。

联立式(25)、式(34)并略去高阶小项可得

(35)

结合辛习涅斯基岩体裂缝中渗流的立方定律，有

(36)

此处考虑的是长轴沿水平方向的裂缝以及流体沿水平方向的流动情况，可忽略重力的影响，则

(37)

(38)

考虑到式(29)，则式(38)可变为

(39)

将式(37)、式(38)、式(39)代入式(35)可得

(40)

由裂缝形状为椭圆得

(41)

(42)

将式(41)、式(42)代入式(40)可得

(43)

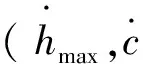
讨论1：

(1) 在条件①的情况下，式(43)可简化为

(44)

求解并代入边界条件，可得在裂缝开度hmax随时间变化忽略裂缝长度c增长时缝内水压沿长轴方向的梯度变化为

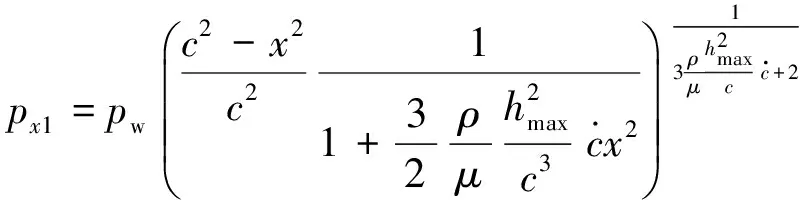
(45)

(2) 在条件②的情况下，则式(43)可简化为

(46)

代入边界条件可得在裂缝长度c随时间变化忽略裂缝开度hmax增长时缝内水压沿长轴的梯度为

(47)

(3) 在条件③情况下，可得裂缝长度和开度hmax同时随时间增长时缝内水压沿长轴的梯度为

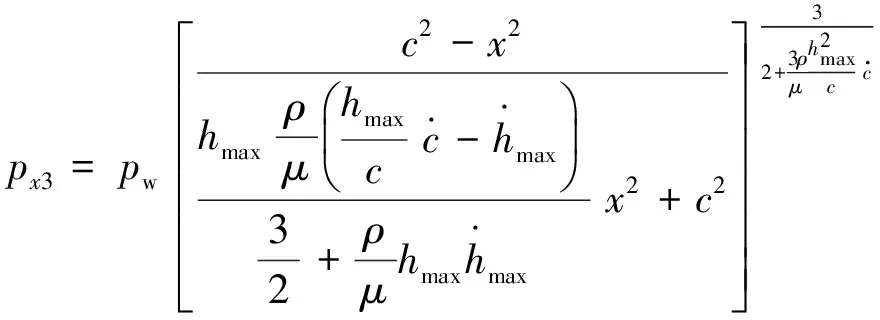
(48)

式(45)、式(47)、式(48)形式复杂，因此有必要通过选择合适的参数使以上3式表现得更直观。

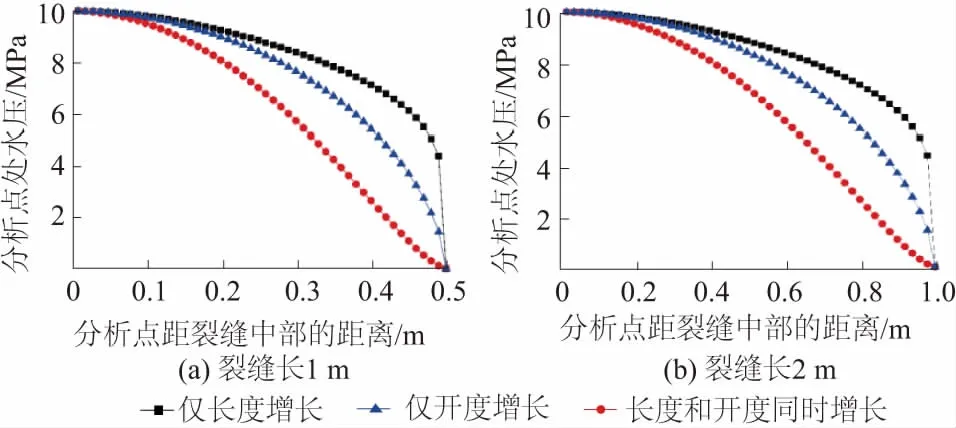
图7 不同裂缝长时的缝内水压分布Fig.7 Distribution of water pressure in cracksof different lengths

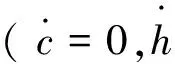
讨论2：

考虑到裂缝开度hmax很小，裂缝生长过程中缝内水压所承受的来自外部的压力几乎不变，也就是说在较短时段t内，即使裂缝有了瞬间生长，裂缝特殊的形状，如狭小的开度、较大的长度加之缝内水体承受着较为恒定的水压、水体的黏滞性不可忽略以及水体在裂缝内运动过程中不可忽略的阻力，这些都将导致裂缝生长过程中新产生的空间无法及时被液体充填，造成缝内暂时的低压或者0压区域。因此本文中求解的结果是可信的。

同时，含水裂缝在生长过程中缝内水体的流动无法跟上裂缝前端的扩展速度，而随着距离裂缝尖端距离的减小，缝内水压不断的减小，在即将靠近裂缝尖端时出现水压陡降现象。据此可推测，自然状况下，如果含水裂缝发生连续性生长那么该生长不可能是由水压胀开导致的。如果裂缝要在自然状况下依靠水力胀开生长，那么至少需要满足2个条件：①缝内初始水压足够胀裂撕开裂缝；②裂缝发生间歇性生长，也就是说裂缝每生长一次之后，必将停一段时间，使得缝内水体有足够的时间充填新形成的裂缝空间并恢复压力。但考虑到自然状况下裂缝长度较大、开度较小、水体依靠自然作用形成的水压力非常有限而裂缝又为大量岩体包围，因此自然状况下裂缝由缝内水压导致的胀开破坏基本没有可能，这也进一步证明了含水裂缝最可能的破坏形式应该是压剪破坏。

4 结 论

(1) 含水裂缝发生拉剪破坏所需的临界水压力大于其发生压剪破坏所需的临界水压力。

(2) 无论是长度和开度同时增长，还是二者之中仅有一个增长，缝内水压在逐渐靠近裂缝尖端时都迅速减小至0。

(3) 含水裂缝自然水力下的胀开必须同时满足2个条件：①裂缝间歇性生长；使水体有时间充填新产生的裂缝空间和恢复压强；②缝内水压足够大，至少能够撕裂不受任何外力作用的含裂缝岩体。

[1] 刘招伟,何满潮,王树仁.圆梁山隧道岩溶突水机理及防治对策研究[J].岩土力学,2006,27(2):228-232.

[2] 孙 谋,刘维宁.高风险岩溶隧道掌子面突水机制研究[J].岩土力学,2011,32(4):1175-1180.

[3]PESENDORFER M, LOEW S. Subsurface Exploration and Transient Pressure Testing from a Deep Tunnel in Fractured and Karstified Limestones (Lotschberg Base Tunnel, Switzerland)[J]. International Journal of Rock Mechanics and Mining Science, 2009, 47(1): 121-127.

[4] 盛金昌,赵 坚,速宝玉.高水头作用下水工压力隧道的水力劈裂分析[J].岩石力学与工程学报,2005,24(7)：1226-1230.

[5] 王建秀,朱合华,唐益群,等.石灰岩损伤演化的断裂力学模型及耦合方程[J].同济大学学报(自然科学版)，2004,32(10): 1320-1324.

[6] 徐栋栋,邬爱清,孙玉杰.某水电站引水隧洞突水数值模拟[J].长江科学院院报,2010,27(8):44-49.

[7] 黄润秋,王贤能,陈龙生.深埋隧道涌水过程的水力破裂作用分析[J].岩石力学与工程学报,2000,19(5):573-576.

[8] 王 瑜,赵其华.某电站坝区左岸深部裂缝特征及成因机理浅析[J].长江科学院院报,2010，27(4):49-52.

[9] 邵 磊,余 挺,迟世春.堆石微裂缝扩展规律及其影响因素[J].长江科学院院报,2016,33(1):115-120.

(编辑：姜小兰)

Law of the Extension of Water-bearing Fractures in Karst Tunnels

ZHANG Zhi-cheng, TANG De-gao, RONG Xiao-li, HUANG Hou-xu

(State Key Laboratory of Explosion & Impact and Disaster Prevention & Mitigation, PLA University of Science and Technology, Nanjing 210007, China)

The mechanisms and mechanical processes of water bursts caused by tensile-shear failure and compression-shear failure of fractures in karst tunnel construction are analyzed according to the hydraulic fracturing principle. Results show that the critical hydraulic pressure of water burst is affected by trend and location of fractures and other factors. Through analyzing the distribution characteristics and gradient of water pressure in the process of fracture propagation, the critical water pressure of tensile-shear failure is revealed greater than that of compression-shear failure. And the crack extension is discontinuous under the action of hydraulic fracturing. The research results are of significance for the prevention and treatment of water burst in the process of tunnel construction.

karst tunnel; water-bearing fracture; water burst; tensile-shear failure; compression-shear failure; water pressure of cracks; discontinuous

2016-04-01；

2016-05-21

国家重点基础研究发展计划“973”项目(2013CB036005)

张志成(1990-)，男，福建福安人，硕士研究生，主要从事岩土力学、地下工程风险管理的学习和研究工作，(电话)15805153502(电子信箱)zzcheng2288@163.com。

10.11988/ckyyb.20160305

2017,34(6):132-137,148

U45

A

1001-5485(2017)06-0132-06