一种基于一致性分片FCM的图像分割算法

2017-06-19丁晓峰何凯霖

重庆邮电大学学报(自然科学版) 2017年3期

关键词：分片邻域像素点

丁晓峰，何凯霖

(电子科技大学成都学院计算机系，成都 611731)

一种基于一致性分片FCM的图像分割算法

丁晓峰，何凯霖

(电子科技大学成都学院计算机系，成都 611731)

针对传统FCM(fuzzyc-means)算法抗噪性差的问题，提出了一种基于一致性分片的模糊c均值聚类算法。为避免额外的空间邻域约束项带来的控制变量设置问题，该算法直接将FCM应用于图像片空间。为减弱空间邻域对图像边缘的模糊，采用基于置信区间的局部多项式交叉近似技术(local polynomial approximation and intersection of confidenec intervals, LPA-ICI)构造自适应形状一致性分片。在脑磁共振图像上的实验表明，与传统的FCM算法相比，该算法具有更高的分割精度和运行效率。

模糊c均值聚类;图像分割;一致性分片;脑磁共振图像

0 引言

模糊聚类方法[1]是一种广泛用于脑磁共振图像分割领域的聚类算法。由于磁共振图像(magnetic resonance images, MRI)具有空间分辨率高和软组织对比度好的优点，因此适合于脑组织容积的估计[2]。自动脑磁共振图像分割的任务是将脑组织主要分为3类：灰质(gray matter; GM)、白质(white matter; WM)和脑脊液(cerebro-spinal fluid; CSF)[3]。

基于模糊聚类的图像分割最早由Zadeh[4]提出，相比于硬聚类分割方法[5]，模糊聚类作为一种软聚类方法得到了广泛的研究，同时在图像分割方面也得到了成功应用。在模糊聚类中，FCM(fuzzyc-means)聚类是最重要的方法之一，能够保留更多的原图信息。但由于没有考虑到图像中的空间信息，因此对噪声非常敏感。为了提高FCM方法的抗噪性，提出了很多结合局部空间信息的改进FCM方法。Ahmed等[6]通过在FCM目标函数中引入一项局部平均约束项来提高FCM方法的抗噪性，简称为BCFCM(biased-field correct fuzzyc-means)。虽然BCFCM方法能够减轻噪声的影响，但算法在每次迭代过程需要计算邻域项，因此具有较高的时间复杂度。为此出现了2种快速的BCFCM方法，即FCM_S1和FCM_S2[7]。在聚类之前先通过均值(FCM_S1)或中值(FCM_S2)滤波得到滤波后的图像；然后，在原图和滤波结果图上采用FCM聚类得到分割结果，从而加速BCFCM算法。Szilágyi等[8]通过将每个像素点聚类转化成对图像的灰度级进行聚类，提出了EnFCM(enhanced fuzzyc-means)快速算法。由于图像灰度级远小于图像像素点个数，因此，该方法有着较快的计算速度。在上述方法中，大多是引入了控制空间约束项的变量来实现的，而该变量的获得必需通过反复的实验来确定。此外，由于均值和中波滤波的因素而影响图像的分割精度。为了克服这些不足，提出了多种改进FCM方法，如MFGFCM(modified fast generalized fuzzyc-means)算法[9]，FCM_AWA(fuzzyc-means_adaptive weighted averaging)算法[10]和SHFCM(spatial homogeneity fuzzyc-means)算法[11]。这些改进方法的基本思想都是自适应构造邻域窗口权重，从而更好地保持图像的边缘。

针对脑磁共振图像的偏移场问题，前人提出了几种带有偏移场纠正的FCM算法。这些方法的基本思路是先对原图取对数，然后在对数域中采用FCM。目的是将乘性偏移场转换成加性，从而通过在FCM目标函数中引入额外的偏移场变量，达到偏移场估计的目的。

针对现有的具有抗噪性的FCM改进算法的局限性[12]，本文提出一种直接基于图像一致性分片空间的FCM聚类方法，即将传统的基于单个像素的距离度量方式改为基于图像片的距离度量方式。这样可以避免引入额外的空间约束变量，同时有效的一致性分片构造方式可以起到边缘保持的目的。脑磁共振图像的分割结果证明了本文提出方法的有效性。

1 基于一致性分片的模糊FCM算法

1.1 FCM算法分析

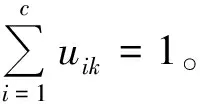
(1)

(1)式中：m∈[1,∞)表示加权指数，取m=1时，表示经典C均值聚类；通过反复测试得出m的最佳选择范围为[1.5,2.5]，一般取m=2；第k个样本与第i类中心vi之间的距离记为dik=‖xk-vi‖A，A范数记为‖·‖A，定义为欧氏距离。

通过对隶属度矩阵U和聚类中心集合V的反复迭代更新来求出FCM目标函数的最优解。

(2)

(3)

(2)-(3)式中：x为样本点，d为样本件的距离，v表示样本中心。对(2)式和(3)式进行不断迭代更新，直到目标函数JFCM小于设定值ε(ε>0)结束。

1.2 一致性分片的构造

(1)式中距离度量函数dik是像素点到聚类中心的欧式距离。为了提高算法的抗噪性，本文将距离度量函数定义在图像片空间，即每个像素点用局部邻域的有序组合向量表示。同时，由于图像片距离度量影响图像边缘的模糊，因此，我们选用形状自适应邻域构造方法来获取同质图像片。

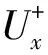
1.3 基于一致性分片的模糊FCM算法

根据1.2构造得到的一致性分片，提出了一种基于一致性分片的FCM聚类(homogeneous pieces based fuzzyc-means,HPFCM)算法。

图1 8方向LPA-ICI各项异性一致性分片构造示意图Fig.1 LPA-ICI consistent image fragmentation in eight directions

(4)

对于图像中的每个像素点都有与之对应的一个q2维向量。那么HPFCM算法的目标函数为

(5)

其中，距离度量函数为

(6)

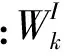
类似的，可以得到HPFCM目标函数的隶属度矩阵和聚类中心的更新公式

(7)

(8)

(7)—(8)式中：d表示像素距离；v表示聚类中心；(8)式可知：本文方法将每个聚类中心扩展为向量，这可以更精确地表示每类聚类中心。

1.4 算法流程

算法实现过程如下。

步骤1 对参数进行初始化。在本文中，取m=2，ε=0.001，c=4。同时，对聚类中心集合V初始化；

步骤2 取图像片邻域窗口半径r=1，由(4)式将图像中的像素点扩展为与之对应的q2维向量，这里q=2r+1；

步骤3 由(7)式对隶属度矩阵U进行更新；

步骤4 由(8)式对聚类中心V进行更新；

步骤5 直到‖Vnew-Vold‖<ε结束迭代并输出结果图像；否则，退回步骤3继续更新迭代。

2 实验与分析

为了验证所提方法的性能，进行仿真对比实验。实验图像来源于Brain Web，脑MR图像的噪声分布服从Rician分布。计算机配置为Intel 酷睿i7四核处理器，4 GByte内存，3.2 GHz 主频，Windows7操作系统，开发环境为Matlab 2012b。

图2显示了FCM及各种改进FCM作用于3幅含不同噪声水平的脑MR图像分割结果比较。HPFCM代表本文提出的方法。SHFCM，FCM_AWA，MFGFCM和HPFCM都是结合空间邻域信息的FCM改进算法，都取半径为1的3×3邻域。图3为专家手工分割结果。

采用Jaccard Similarity(JS)方法和Dice Coefficient(DC)方法对图像分割精度进行定量分析，其度量公式依次为

(9)

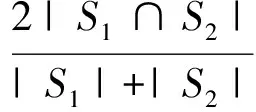
(10)

(9)式和(10)式中：S1和S2为2幅图像的分割结果，其与Brain Web中的手工分割结果比较；|·|表示相应区域像素点的总个数。

采用系统运行时间对算法执行效率进行度量。

表1和表2分别为各种方法分割结果的精度(JS和DC)比较。其中，每一行代表一种算法，每一列代表一种指标下的性能。最后一列是该算法的平均性能。表3为各种方法分割时间的比较。每行是不同的算法，每列代表不同指标下的分割时间。

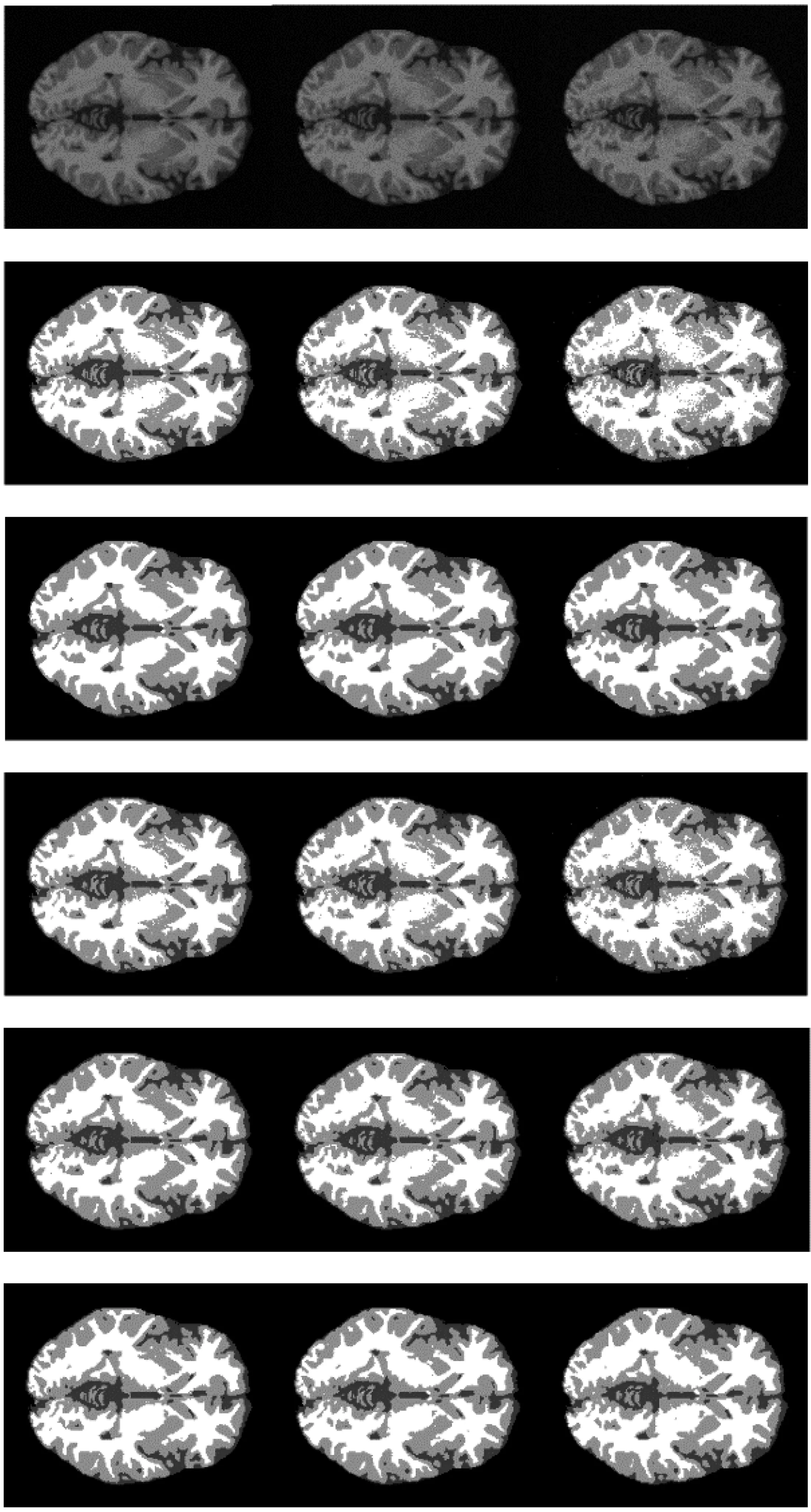
注：第1行从左到右为含噪分别为5%，7%和9%的噪声图像。第2到第6行分别为FCM，SHFCM，FCM_AWA，MEGFCM和HPFCM分割结果。图2 脑磁共振图像分割结果比较Fig.2 Results comparison of brain magnetic image segmentation

注：从左到右分别是CSF，GM和WM的分割结果图3 图2的标准分割结果Fig.3 Standard segmentation results of Fig.2

从上述实验结果可知：对于脑脊液(CSF)来说，当噪声水平较低时，传统的FCM算法的分割精度要高于各种改进FCM算法，因为CSF具有很多细小的结构(见图3)，邻域信息引入会导致细小结构的丢失，所以各种改进FCM算法在克服噪声的同时也平滑了CSF的细小结构，导致分割结果反而不如FCM算法。相对于灰质(GM)和白质(WM)来说，各种改进FCM算法相对于传统FCM算法的优点就体现得很明显，而本文方法在大多数情况下又要优于其他几种改进FCM算法，同时本文方法没有引入额外的控制变量，便于自动化处理。从平均分割精度比较可知：本文方法除了CSF的分割精度不如FCM外，GM和WM的分割精度都是最高的；从表3的结果可知，本文提出的方法在不同参数设置下均花费最短的分割时间，因此执行效率最高。

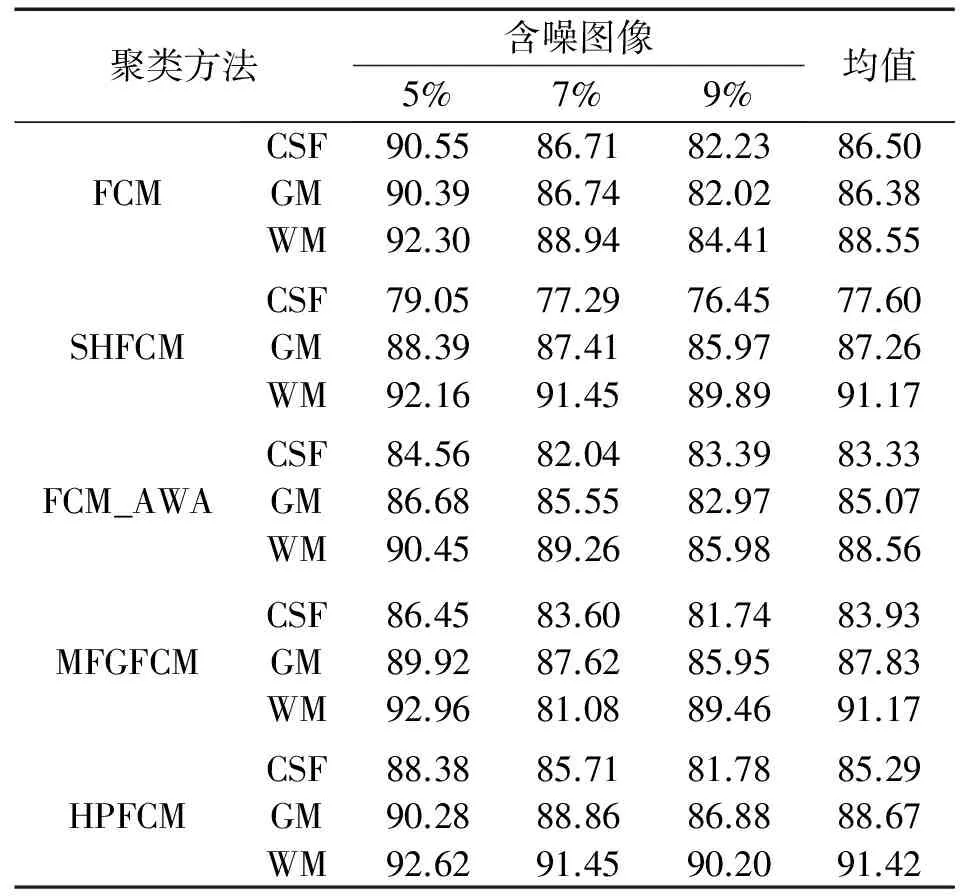
表1 FCM，SHFCM，FCM_AWA，MEGFCM和HPFCM分割结果精度比较(JS，单位：%)

表2 FCM，SHFCM，FCM_AWA，MEGFCM和HPFCM 分割结果精度比较(DC，单位：%)

表3 FCM，SHFCM，FCM_AWA，MEGFCM和HPFCM分割时间比较

3 结论

本文提出了一种基于一致性分片的FCM算法，并将其应用于脑磁共振图像的分割中。通过将现有的FCM距离度量函数扩展到图像片空间，从而避免引入额外的局部邻域约束项来达到抗噪的目的。另外，采用了具有抗噪性的形状自适应的邻域生成算法构造一致性分片空间，使构造的一致性分片具有较好的抗噪能力。脑磁共振图像的分割结果表明：对于灰质和白质的分割，该方法在分割精度上要优于其他方法；对于脑脊液的分割，该方法不如传统的FCM，但优于其他结合空间邻域信息的改进FCM算法。如何克服结合空间邻域信息导致细节丢失而引起的脑脊液分割精度下降问题将是下一步的工作重点。

[1] 江少锋,王文辉,冯前进,等.基于改进BET算法的MR颅脑图像脑组织自动提取[J].中国图像图形学报,2013,14(10): 2029-2034. JIANG S F,WANG W W,FENG Q J.An MR image extraction approach based on an improved BET algorithm[J].Journal of Image and Graph,2013,14(10):2029-2034.

[2] SIEGEL R, NAISHADHAM D,JEMAL A. Cancer statistics[J]. CA:A Cancer Journal for Clinicians, 2013,63(1):11-30.

[3] 蒋世,易法令,汤浪平,等.基于图像分割的MRI脑部图像肿瘤提取方法[J].计算机工程,2012,36(7):217-219. JIANG S, YI F L, TANG L P, et al. An MRI image extraction approach based on image segmentation[J]. Computer Engineering, 2012, 36(7):217-219.

[4] ZADEH L A. Fuzzy sets[J]. Information and Control, 1965,8(3): 338-353.

[5] PHAM D L, XU C Y, PRINCE J L. A survey of current methods in medical image segmentation[J]. Annual Review of Biomedical Engineering,2012,2(1): 315-337.

[6] MA L,STAUNTON R C.A modified fuzzy C-means image segmentation algorithm for use with uneven illumination patterns [J].Pattern recognition,2013,40(11):3005-3011.

[7] CHEN S C, ZHANG D Q. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure [J]. IEEE Transactions on Systems, 2014,15(3): 353-358.

[9] 张信顺.基于阈值速度函数的脑肿瘤水平集分割[J].计算机测量与控制,2012,28(1):26-37. ZHANG X S. A image segmentation algorithm based on threshold function[J]. Computer measurement and control, 2012, 28(1):26-37.

[10] 段锐,管一弘.医学图像自动多阈值分割[J].计算机应用,2012,28(S2):204-205. DUAN R, GUAN Y. Multiple threshold segmentation for Medical Images[J]. Computer Application, 2012, 28(S2):204-205.

[11] JAYADEVAPPA D,KUMAR S S, MURTY D S.A Hybrid segmenta- tion model based on watershed and gradient vector flow for the detection of Brain tumor [J].International journal of Signal processing, Image processing and Pattern Recognition, 2014,2(3): 29-42.

[12] KHOTANLOU H, COLLIOT O, ATIF J, et al. 3D brain tumor segmentation in MRI using fuzzy classification, symmetry analy- sis and spatially constrained deformable models[J].Fuzzy Sets and Systems,2013,160(10):1457-1473.

(编辑：张诚)

A homogeneous pieces based FCM algorithm for image segmentation

DING Xiaofeng, HE Kailin
(Department of Computing, Chengdu College of University of Electronic Science and Technology of China, Chengdu 611731, P.R. China)

To address the problem that existing FCM algorithms have poor noise immunity, we propose a novel fuzzyc-means clustering (FCM) algorithm based on homogeneous pieces. The algorithm directly applies FCM in the imaging space, so that the control variable setting problem caused by the introduction of additional space neighborhood constraints is avoided. In addition, in order to abate the fuzzy effect to the edge of image by space neighborhood, the local polynomial approximation-intersection of confidence intervals (LPA-ICI) based on confidence interval is adopted to construct the homogeneous piece with adaptive form. Through the segmentation of brain magnetic resonance imaging, the experimental results show that, compared with the traditional FCM algorithm, this algorithm can make accurate segmentation to the brain magnetic resonance image.The method is useful and effective for MRI image segmentation.

fuzzyc-means clustering; image segmentation; homogeneous piece; brain magnetic resonance image

2016-09-10

2017-04-13 通讯作者：丁晓峰 dingxf_cd@126.com

10.3979/j.issn.1673-825X.2017.03.015

TP391

1673-825X(2017)03-0377-05