HPFL加固受火RC梁刚度及挠度研究
2017-06-19曾令宏蒋朝阳
曾令宏,蒋朝阳
(湖南大学 土木工程学院,湖南 长沙 410082)
HPFL加固受火RC梁刚度及挠度研究
结合国内外对火灾后钢筋混凝土结构中混凝土和钢筋力学性能的研究,分别采用三台阶模型和二台阶模型对火灾后混凝土和钢筋的弹性模量进行简化计算.根据简化计算模型和等效弹性模量法,对受火后钢筋混凝土梁截面的弹性模量进行等效,得到受火后钢筋混凝土梁截面的弹性模量.根据有效惯性矩法,对高性能复合砂浆钢筋网加固受火RC梁开裂前和开裂后的截面进行等效换算,将受拉区钢筋和全截面的高性能复合砂浆钢筋网换算成弹性模量为混凝土弹性模量的换算截面.在考虑剪切变形影响的前提下,对高性能复合砂浆钢筋网加固受火RC梁的截面刚度和挠度进行理论推导,并结合实验数据验证理论公式的合理性.分析结果表明,推导所得的计算公式与试验数据基本吻合.
截面刚度;高性能复合砂浆钢筋网;火灾;加固
高性能复合砂浆钢筋网(HPFL)加固法是通过在混凝土结构构件的外部增加高性能复合砂浆薄层,并搭配钢筋网来提高混凝土结构构件承载力的一种加固方法.高性能复合砂浆具有良好的流动性、较强的粘结性、防火耐高温性能好以及收缩小等优点,与旧混凝土界面能够很好地结合,共同工作.HPFL加固法是一种新型的加固方法,具有很好的实际应用性.
钢筋混凝土受弯构件挠度一般按照国家规范《混凝土结构设计规范》(GB 50010-2010)中的计算方法计算,只考虑弯曲变形的影响,忽略剪切变形的影响,只适用于跨高比大于5的普通钢筋混凝土构件.当钢筋混凝土梁的跨高比比较小时,剪力引起的变形就不可忽略,特别是钢筋混凝土梁在斜裂缝出现之后,剪切刚度迅速下降,钢筋混凝土梁的剪切变形迅速增大,甚至在梁的总变形中占主导作用[1].本文考虑钢筋混凝土梁的剪切变形的影响,给出了HPFL加固受火RC梁刚度及挠度的计算方法,并用实验数据进行了验证.
1 受火后钢筋混凝土的性能
1.1 受火后混凝土的弹性模量
国内外文献认为高温后混凝土的弹性模量会随着遭受火灾时温度的升高而下降幅度越来越大;随着温度的升高,700 ℃以后混凝土的弹性模量会保持在一个很低的水平[2-4].高温对混凝土弹性模量的影响具体见图1.
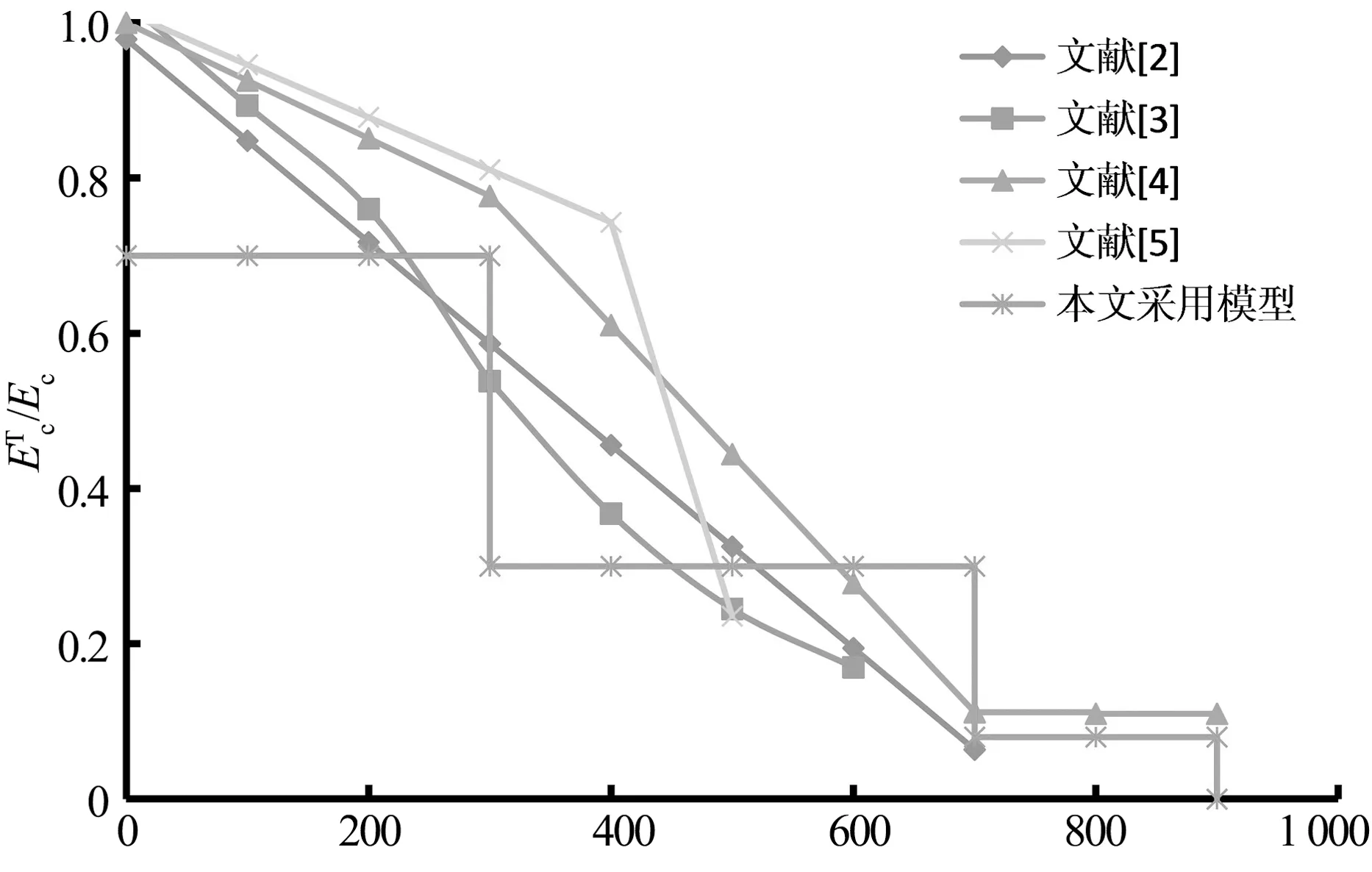
T/℃
1.2 受火后混凝土的泊松比
吴波[5]通过试验对高温后混凝土的泊松比和体积应变的变化进行了总结分析,经过分析发现:温度对高温后混凝土泊松比的变化有较大的影响,300 ℃范围以内,混凝土应力σ为0.5fc(T)时的泊松比在0.12~0.25;当温度超过300 ℃时,高温后混凝土的泊松比将随着σ/fc(T)的增大而大幅度的增大,但与具体的温度高低没有明显关系.温度超过300 ℃时,高温后的混凝土在荷载达到峰值应力的60%后,体积应变变化就会出现混乱,混凝土的裂缝发展将会进入不稳定发展阶段,这类混凝土构件要慎重考虑承受长期荷载.经过对试验结果的整理分析和回归拟合,给出了高温后混凝土的泊松比ν与荷载及峰值应力比σ/fc(T)的数学计算关系.
1.3 受火后钢筋的弹性模量


T/℃
2 刚度及挠度计算
2.1 简化模型
本文结合国内外已有的计算模型,对火灾(高温)后混凝土的弹性模量与温度的关系采用了三台阶模型,对火灾(高温)后钢筋抗拉强度、钢筋弹性模量与温度的关系采用了二台阶模型,因为建筑火灾的温度一般为800~1 000 ℃,因此只考虑受火RC梁1 000 ℃内的计算模型简化[7].火灾(高温)后混凝土的泊松比ν取荷载与峰值应力比为0.5(σ/fc(T)=0.5)时的值,取为ν=0.18.在不同条件下混凝土和钢筋受火灾(高温)冷却后的弹性模量与受火时温度的关系可以简化分别如图1和图2;计算公式简化分别如式(4)(5)所示.
混凝土的弹性模量:
(1)
钢筋的弹性模量:
(2)
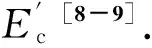
A=bh
(3)
A3=bT3hT3
(4)
A7=bT7hT7-bT3hT3
(5)
(6)
式中:b为原钢筋混凝土截面宽度;h为原钢筋混凝土截面高度;bT3,hT3分别为原钢筋混凝土截面受火时300 ℃等温线的宽度、高度;bT7,hT7分别为原钢筋混凝土截面受火时700 ℃等温线的宽度、高度;A为原钢筋混凝土截面面积;A3为原钢筋混凝土截面受火时,0~300 ℃等温线范围内的面积;A7为原钢筋混凝土截面受火时,300~700 ℃等温线范围内的面积.

图3 受火钢筋混凝土梁原截面图
(7)

图4 受火RC梁300 ℃和700 ℃等温线位置
2.2 四面加固梁截面刚度计算
根据等效原则,HPFL加固受火钢筋混凝土梁,在受拉区裂缝出现前后原截面和换算截面分别如图5~图7所示.

图5 原加固梁截面

图6 裂缝出现前换算截面

图7 裂缝出现后换算截面
构件出现裂缝之前,全截面的高性能复合砂浆和混凝土受力.受拉区钢筋面积和全截面的高性能复合砂浆面积都应换算成弹性模量为混凝土弹性模量的换算面积.除了原位置的钢筋和高性能复合砂浆的面积之外,需在截面同一高度处增设附加面积.钢筋和高性能复合砂浆面积上的应力与相应的截面高度的混凝土的应力相等.以此构成换算混凝土截面和原HPFL加固受火混凝土梁截面力学性能的等效[10].截面换算过程如下:
(8)
(9)
n1=Es/E0
(10)
n2=Esm/E0
(11)
n3=Ecm/E0
(12)

开裂前换算截面的总面积为:
A0=(b+2t)(h+2t)+(n1-1)As+(n2-1)
(Asm1+Asm2) +2(n3-1)(Acm1+Acm2)
(13)
式中:b为加固前钢筋混凝土梁截面宽度,详见图4;t为HPFL加固层厚度,详见图5;h为加固前钢筋混凝土梁截面高度,详见图5;As为原钢筋混凝土梁截面受拉钢筋面积,详见图5;Asm1为加固梁底部钢丝网面积,详见图6;Asm2为加固梁双侧面受拉区钢丝网总面积,详见图6;Acm1为加固梁底部高性能复合砂浆加固层面积,详见图6;Acm2为加固梁单侧高性能复合砂浆加固层面积,详见图6.
受压区高度x0由拉、压区对中和轴的面积矩相等的条件确定:

(14)
式中:h0为原钢筋混凝土梁截面的有效高度.
由式(14)可求得:

(15)
则开裂前换算截面的惯性矩I0为:

(16)
所以,HPFL加固受火钢筋混凝土梁开裂前截面的抗弯刚度B0为:
B0=E0I0
(17)
构件出现裂缝后,假定裂缝截面上受拉区的混凝土和高性能复合砂浆完全退出工作,只有钢筋承担拉力,将钢筋的换算面积置于相同的截面高度,得到的换算截面如图7所示.
开裂后换算截面的总面积为
Acr=(b+2t)(xcr+t)+(n3-1)Acm1+

(18)
对此裂缝截面的受压区高度xcr可用同样方法确定:

(19)
由式(19)可得到关于xcr的方程式:
(20)
解关于xcr的一元二次方程式可知:


(21)
则裂缝截面的换算惯性矩Icr为:

(22)
所以,HPFL加固受火钢筋混凝土梁裂缝截面的抗弯刚度Bcr为:
Bcr=E0Icr
(23)
Branson[11]在对试验结果进行分析的基础上,提出了下面计算开裂钢筋混凝土梁和单向板有效惯性矩的公式:

(24)
式中:Mcr为构件截面开裂弯矩;Ma为构件截面最大弯矩(Ma>Mcr);β=3.
因此,四面加固梁截面有效抗弯刚度为:
Be=E0Ie
(25)
HPFL四面加固受火钢筋混凝土梁开裂前截面的抗剪刚度为:
D0=G0A0
(26)
HPFL四面加固受火钢筋混凝土梁开裂后截面的抗剪刚度为:
Dcr=G0Acr
(27)
根据文献[1],裂缝出现后,随荷载F的增大,实测构件的荷载-挠度曲线的斜率会越来越小,这说明构件的剪切刚度随着加载荷载F的增大而越来越小,呈反相关关系.假定此时剪切刚度De表示如式(28):
(28)
式中:Fcr为构件出现裂缝时的荷载;F为计算构件挠度时的荷载.
2.3 四面加固梁截面挠度计算
由结构力学理论可知,根据虚功原理,在荷载作用下平面杆系结构位移ΔkP的计算公式可以表达如式(29):
(29)
式中:ΔkM为在M作用下构件的位移;ΔkQ为在Q作用下构件的位移;ΔkN为在N作用下构件的位移;Mk,MP为构件分别在单位力、P作用下的弯矩;Qk,QP为构件分别在单位力、P作用下的剪力;Nk,NP为构件分别在单位力、P作用下的轴力.
对于HPFL加固受火钢筋混凝土梁,N=0.考虑剪切变形时,由于构件非弹性工作和斜裂缝的出现使剪切变形变大,因此,引入修正系数β(x)[12].根据试验取经验值:无斜裂缝和横向裂缝时,β(x)=1;只有斜裂缝而无横向裂缝的构件区段,β(x)=4.8;只有横向裂缝或兼有横向和斜向裂缝的区段,β(x)=3B/BT,这里B为带裂缝工作的刚度,BT为裂缝刚形成的刚度.聂建国等[13]通过试验,并考虑加固形式对加固梁截面的剪切刚度形成的影响,对修正系数β(x)的值进行了修正,短期荷载作用下修正系数β(x)=2(1+2α),其中α为初始应力水平系数,长期荷载作用下的修正系数取短期荷载作用下修正系数的2倍.
HPFL加固受火钢筋混凝土梁的挠度f可以表达如式(30):
(30)
式中:fM为构件在弯矩作用下产生的位移;fV为构件在剪力作用下产生的位移;k为剪切效应系数,对于矩形截面梁取1.2.
3 与试验结果对比
根据文献[14]中所做试验,试验采用的高性能复合砂浆的弹性模量Ecm=2.0×104MPa,混凝土的弹性模量Ec=2.55×104MPa,纵向钢筋和钢筋网的弹性模量Es=Esm=2.0×105MPa.试验梁原构件的截面尺寸为b×h=200mm×400mm,试验梁设计为伸臂梁(考虑剪切变形的影响),跨度为4 400mm,净跨为4 200mm,其中伸臂段为500mm,加载位置如图8所示,试验梁未加固时的具体尺寸及配筋情况如图9所示,试验梁加固后的尺寸及加固配筋情况如图10所示.构件在伸臂段及集中力作用段(AB段、BC段)采用四面加固形式,其他段采用U型加固形式.
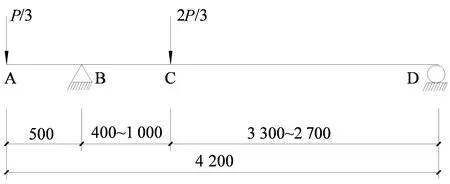
图8 试验梁加载位置示意图
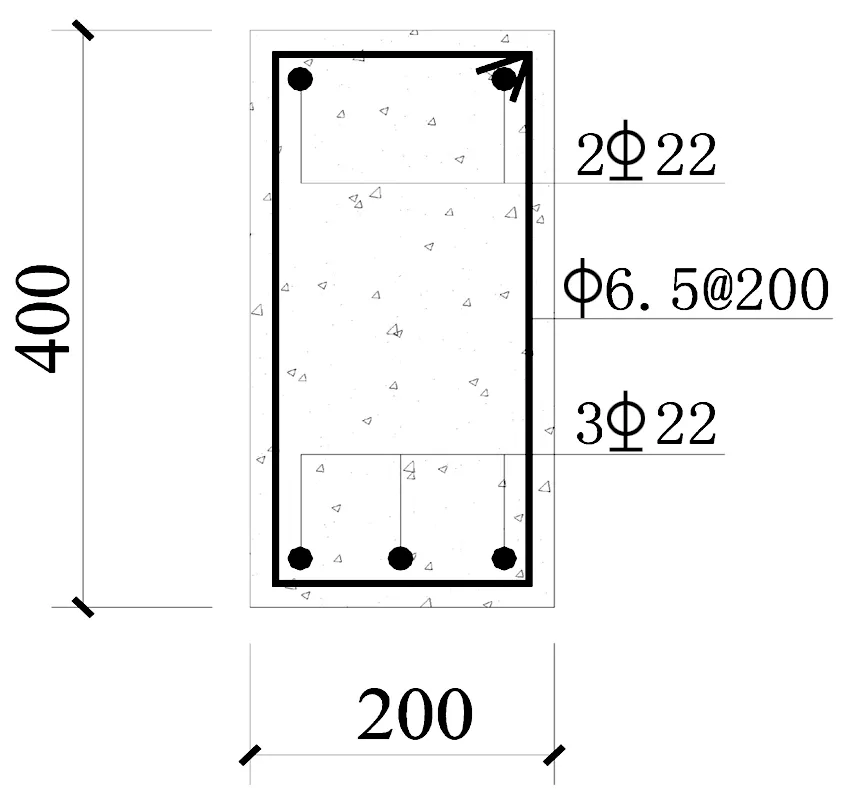
图9 试验梁未加固时截面配筋

图10 试验梁加固截面配筋
试验采用重物吊篮加载法,加载装置为杠杆,通过力分配梁将荷载分传给试验构件.试验加载时按照以下要求:加载达到开裂试验荷载计算值的 90%后,每级加载值按照使用状态短期试验荷载值的5%进行加载;每级加载值不大于使用状态短期试验荷载值的20%;加载达到承载力试验荷载计算值的 90%以后,每级加载值为使用状态短期试验荷载值的 5%;每级荷载加载后的持续时间为15min;构件的自重和作用在其上的分配梁的重力,作为试验荷载的一部分[14].
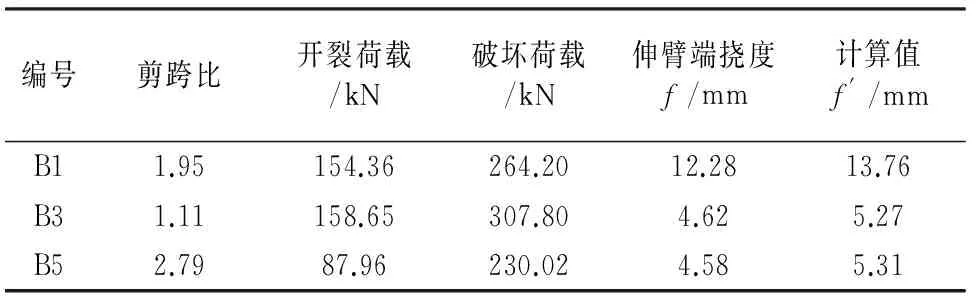
表1 试验结果与理论计算结果
由表1可知,f/f′分别为0.892,0.877和0.863.
由上述计算结果可以看出,所推导的公式与试验值比较吻合,且偏于保守,试验值比理论计算值低约10.8%~13.7%.
4 结 论
本文考虑受火后混凝土和钢筋弹性模量以及混凝土泊松比的变化,根据等效原则和结构力学理论,对高性能复合砂浆钢筋网加固受火RC梁考虑剪切变形影响的截面抗弯刚度、抗剪刚度和挠度的计算公式进行了理论推导,并得出了以下结论:
1)考虑火灾对混凝土和钢筋材料力学性能的影响,根据等效原则,提出简化计算模型.
2)基于有效惯性矩法和结构力学理论,推导出HPFL四面加固受火后RC梁的截面抗剪刚度、抗弯刚度以及挠度的计算公式,以便实际工程使用.
3)通过已有的试验数据验证了所提出的挠度计算公式的合理性,从而验证了截面刚度计算公式的合理性.
[1] 熊进刚,伍卫秀,程文瀼.钢筋混凝土短梁刚度和变形的分析与计算[J].建筑结构,2003,33(8):22-24.
XIONGJingang,WUWeixiu,CHENGWenrang.AnalysisandcalculationofshortRCbeam’sstiffnessanddeformation[J].JournalofBuildingStructures,2003, 33(8):22-24.(InChinese)
[2] 侯高峰,韦军.高温后不同强度等级混凝土力学性能的试验研究[J].工程质量,2010,28(3):68-70.
HOUGaofeng,WEIJun.Experimentalresearchofmechanicalpropertiesofconcretewithdifferentratingafterhightemperature[J].ConstructionQuality, 2010,28(3):68-70.(InChinese)
[3] 徐彧,徐志胜,朱玛.高温作用后混凝土强度与变形试验研究[J].长沙铁道学院学报,2000,18(2):13-16.
XUYu,XUZhisheng,ZHUMa.Experimentalinvestigationofstrengthandreformationofconcreteafterhightemperature[J].JournalofChangshaRailwayUniversity, 2000,18(2):13-16.(InChinese)
[4] 吴波,袁杰,王光远.高温后高强混凝土力学性能的试验研究[J].土木工程学报,2000,33(2):8-12.
WUBo,YUANJie,WANGGuangyuan.Experimentalstudyonmechanicalpropertiesofhighstrengthconcreteafterhightemperature[J].ChinaCivilEngineeringJournal, 2000,33(2):8-12.(InChinese)
[5] 吴波.火灾后钢筋混凝土结构的力学性能[M].北京:科学出版社,2003:7-60.
WUBo.Mechanicalpropertiesofreinforcedconcretestructureafterfire[M].Beijing:SciencePress, 2003:7-60.(InChinese)
[6] 沈蓉,凤凌云,戎凯.高温(火灾)后钢筋力学性能的评估[J].四川建筑科学研究,1991,17(2):5-9.
SHENRong,FENGLingyun,RONGKai.Assessmentofthemechanicalpropertiesofsteelafterhightemperature(fire)[J].SichuanBuildingScience, 1991, 17(2):5-9.(InChinese)
[7] 翟越,艾晓芹,邓子辰,等. 受火温度和冷却方式对混凝土抗压强度影响[J]. 湖南大学学报:自然科学版,2014,41(11):74-80.
ZHAIYue,AIXiaoqin,DENGZichen,etal. Influences of cooling mode and high temperature on concrete compressive strength[J]. Journal of Hunan University: Natural Sciences, 2014, 41(11): 74-80. (In Chinese)
[8] 谢和平.岩石混凝土损伤力学[M].徐州:中国矿业大学出版社,1990:116-146.
XIE Heping.Damage mechanics of rock and concrete[M]. Xuzhou: China University of Mining and Technology Press,1990:116-146.(In Chinese)
[9] LEMAITRE J.How to use damage mechanics[J].Nuclear Engineering and Design,1984,80(03):233-245.
[10]尚守平,刘沩. HPFL加固混凝土结构斜截面承载力计算及工程应用[J]. 湖南大学学报:自然科学版,2011,38(2):1-7.
SHANG Shouping, LIU Wei. Calculation of diagonal section resistance and engineering application of strengthening restructures using HPFL[J]. Journal of Hunan University: Natural Sciences, 2011, 38(2): 1-7.(In Chinese)
[11]BRANSON D E. Instantaneous and time-dependent deflections of simple and continuous reinforced concrete beams[R]. Alabama: Alabama Highway Department/US Bureau of Public Roads, 1963: 1-78.
[12]王传志,滕志明.钢筋混凝土结构理论[M].北京:中国建筑工业出版社,1985:350-351.
WANG Chuanzhi, TENG Zhiming. Theory of reinforced concreted concrete structure[M]. Beijing: China Architecture and Building Press, 1985:350-351.(In Chinese)
[13]聂建国,蔡奇,张天申,等.高强不锈钢绞线网-渗透性聚合砂浆抗剪加固的试验研究[J].建筑结构学报,2005, 26(2):10-17.
NIE Jianguo,CAI Qi,ZHANG Tianshen,etal. Experimental study on shear behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures, 2005, 26(2) :10-17.(In Chinese)
[14]叶蓁.高性能复合砂浆钢筋网加固伸臂梁受剪性能的试验研究[D].长沙:湖南大学土木工程学院,2007:10-35.
YE Zhen. The experimental research on shear strengthing of the cantilever beam with the high performance ferrocement [D]. Changsha: College of Civil Engineering, Hunan University, 2007: 10-35. (In Chinese)
Study on Reinforced Concrete Beams’ Stiffness and Deflection Strengthened with High-performance Ferrocement Laminate After the Fire
ZENG Linghong†, JIANG Chaoyang
(College of Civil Engineering, Hunan University, Changsha 410082, China )
Combined with domestic and international research on the mechanical properties of concrete and steel after fire, a three-step model and a two-step model were used to calculate the elastic modulus of concrete and steel simply, respectively. According to the simplified calculation model and the equivalent elastic modulus method, an equivalent cross-section elastic modulus of reinforced concrete beams was obtained after fire. Based on the effective moment of inertia method, the cross section of the reinforced concrete beam was equivalently translated before and after the reinforced concrete beam cracked. Area of the whole cross-section mortar and the reinforced area of tension zone were translated to the effective area whose modulus of elasticity is the concrete modulus of elasticity. Through the experiment data, design formula of the stiffness and deflection of the reinforced concrete beam with high-performance ferrocement laminate after fire was deduced and verified. The calculation results are in good agreement with the experimental ones.
stiffness; high-performance ferrocement laminate; fire; strengthening
1674-2974(2017)05-0037-07
10.16339/j.cnki.hdxbzkb.2017.05.005
2016-04-09 基金项目:国家自然科学基金青年基金资助项目(51108173), National Natural Science Foundation of China(51108173) 作者简介:曾令宏(1978-),男,湖南衡阳人,湖南大学副教授,工学博士 †通讯联系人,E-mail: mikema21@126.com
曾令宏†,蒋朝阳
(湖南大学 土木工程学院,湖南 长沙 410082)
TU375
A
