用历史名题推开数学文化的窗——“鸡兔同笼”赏析课教学实践

◇顾卫华

用历史名题推开数学文化的窗
——“鸡兔同笼”赏析课教学实践

◇顾卫华

数学文化是指人类在数学行为活动的过程中所创造的物质产品和精神产品。物质产品指数学命题、数学方法、数学问题和数学语言等知识性成分；精神产品指数学思想、数学意识、数学精神和数学美等观念性成分。以此定义审视现在的课堂，很明显我们对“物质产品”一直非常重视，长抓不懈；但对于“精神产品”还是有点“虚”，不够扎实。

“鸡兔同笼”出自《孙子算经》，该题虽不具有实际意义，却可以成为一类问题的数学模型。同时，题目情节有趣但不简单，解答有挑战但不艰涩，成为历史名题实至名归，实在是体会数学文化的极好载体。在苏教版教材中，此题被安排在六年级下册“解决问题的策略”单元的“你知道吗”中，仅仅作为附属知识出现，有点儿可惜。于是，我大胆尝试，以此为载体上了一节“名题赏析”课，着力引导学生体会数学文化中那些“虚”的成分，感悟数学内在的理性美。

一、导入

（直接出示下题，如图1）

图1

师：题目的意思明白吗？谁来说说？

生1：鸡和兔在一个笼子里，一共有35个头，有94只脚，求鸡和兔各有多少只。

师：（竖起大拇指）不错，这可是一道千古名题，今天我们一起来研究、欣赏它。为了方便，老师把数改小一点儿。

（师出示：若干只鸡和兔同在一个笼子里，从上面数，有12个头；从下面数，有34只脚。笼中鸡和兔各有多少只）

师：为什么这会成为一道名题呢？如果老师把题目改一下，你觉得还能吸引人吗？（如图2）

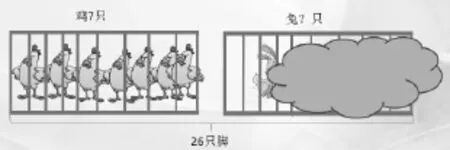
图2

生2：直接就能求出兔有多少只了，不好玩了。

师：你的意思是说，名题之所以有名，是因为有点儿挑战，是吗？

生2：是呀，否则就太没有意思了。

师：非常棒！学习数学有时就需要这种迎难而上的精神。你们愿意接受“鸡和兔”的挑战吗？请独立完成，准备展示你的想法。

（生独立完成，师巡视，捕捉亮点）

二、分享

师：谁愿意来分享你的想法？

（生1的想法见图3）

图3

生1：我用的是列举法。不知道鸡、兔的只数，我就想，如果鸡有12只，那么兔就是0只，总脚数就是2乘12，24只。而题目告诉我们一共有34只脚，显然不对，说明鸡不是 12只。然后就继续列举，最后到7只鸡和5只兔的时候正好是34只脚，那就说明鸡7只、兔5只。请大家和我交流。

生2：我觉得你说得很棒，但是我从 12只兔子开始列举也是可以的。

生1：我赞同你的想法。

师：听了你们的对话，老师有个疑问，为什么你们都选择从12只鸡或兔开始列举呢？

生2：我觉得从全部是兔考虑，比较容易。

师：老师发现你很有数学的眼光，确实从极端情况考虑往往比较——

生：（齐）容易。

师：谁还有不同的想法呢？

生3：我来，我是列式计算的。（如图4）

图4

生4：很棒，我还可以先假设全是兔，那自然总脚数就变多了。

师：真了不起！你们的发言都很精彩。历史上，曾经流传有很多解答，大家想开开眼界吗？

三、欣赏

（课件用菜单方式出示：画图法、鸡翅当脚法、砍脚法）

师：这是六年级的题目，一年级的小朋友也会做。不信？请看！（如图5）

图5

师：谁来解释他是怎么想的？

生1：我来解释。先全部画成两只脚的鸡，一共12只，然后再增加脚数，黑色部分就是比实际少的10只脚，每只鸡添2只脚，就变成了兔，所以就有5只兔。

（课件出示“鸡翅当脚法”，录音配动画：兔有4只脚，而鸡只有2只脚，这岂不是太不公平了吗？鸡还有2只翅膀呢!如果把2只翅膀也看成脚，那么鸡也就有了4只脚。这样……）

师：谁是数学家的知音？

生2：我明白了。12只动物就有了4乘12等于48只脚！咦？已知有34只脚呀，为什么多了14只脚呀？哦，其实这14只，不是脚，是假装成脚的翅膀呀。那么鸡就是14÷2=7（只），剩下的5只便全是兔了。

（课件出示“砍脚法”，录音配动画：如果把每只动物都砍成2只脚，这样所有的动物都是2只脚……）

师：大家听明白了吗？

（生回答，略）

四、分析

师：课始我们分析过，“鸡兔同笼”之所以成为名题，是需要解答者同时满足 “头12个”“脚34只”这两个要求！数学中是怎么处理这种挑战的？请大家比比刚才我们所经历的各种解法，它们有什么相同的地方？

生1：我觉得都是在假设。

师：具体说说。

生2：你们看，不管是哪种方法，都会先假设全部是鸡或者兔，然后求出总脚数，发现比已知的总脚数少或者多，最后再换。

师：有道理！换的时候有点不一样而已。

生3：我觉得“鸡翅当脚法”其实就是假设成全是兔，因为当鸡把翅膀当成脚时，就相当于全是兔了。

师：你总结得很有水平，那老师想问你，为什么要假设呢？

生3：因为，不能一下子知道鸡和兔各有几只。

师：数学学习需要不断追问。为什么不能一下子求得鸡和兔的只数呢？

生3：因为不能同时满足 “头12个”“脚 34只”这两个要求，除非运气特别好，一猜就中了！

师：对！不能同时满足“头12个”“脚34只”这两个要求。面对这个困难，所有人都干了同样的一件事，是什么？

生4：我觉得都是在算脚。

师：算脚？

生4：对呀，算总脚数有多少。只要算到总脚数是34，就可以了。

师：那头呢？

生4：头一直是12个呀！

师：哈哈，看来当无法一下子满足“头”和“脚”两个条件时，我们首先选择了“头”——满足“头12个”这个条件。假设12个头全部是一种动物的，然后去设法调整脚数，让总脚数慢慢地满足“脚34只”这个条件。只不过调整的方式可能有所不同，有的是一次性调整到位，有的是一只只调整。回味一下，是不是这样呢？

（生再次比较各种解法，频频点头）

师：嗯，看来我们已经把握住最关键的部分了。各种解法各有不同，所以有不同的名称，什么列举法、画图法、砍脚法等，但所体现出来的数学智慧是一样的，都是先满足一个条件，然后设法满足第二个条件。当你把握了这个规律的时候，我们回头再来看也许会有新的收获。比如说，先前我们都是从极端的情况假设。难道只有这一条路吗？

生5：我有新的办法了，反正都是12个头，我就平分一下，6只鸡和6只兔，这样一共有12+24= 36（只）脚，不对。鸡增加1只，兔减少1只，就正好是34只脚了。请大家和我交流。

生6：好像你的方法更简捷些。

师：是呀，因为你没有从极端情况开始考虑，而是选择了对半分，反而离正确答案更近了一些。不过老师请教你，当你算出36只脚时，为什么能想到增加鸡的只数而不是增加兔的只数？这是特别有智慧的地方。

生5：因为总脚数多了2，所以要减少，那么就要把兔子换成鸡。1只兔子换成1只鸡。

师：哦，原来是这样，把1只兔子换成1只鸡，总脚数就减少了2。还能怎样假设？

（生纷纷举手回答）

师：好了，找到规律后，新的方法就太多了。但万变不离其宗，他们都是如何处理的？

生7：都是先满足一个条件，然后设法满足第二个条件。

五、推广

师：这鸡可不是一般鸡，这兔也是非凡兔，被你们逼急了，它们去了趟花果山，学了七十二般变化，藏在了以下4个场景中。你们还能找到它们吗？

（师提供菜单式选择，分别是 “日本”“春游”“投篮”“下棋”。生选“日本”，师课件出示：有一群鹤和乌龟都圈在一个笼子里。从上边数脑袋是35个，从下边数脚是94只。问乌龟和鹤各是多少只）

生：很简单，鹤就是鸡，因为有2只脚；乌龟就是兔，有4只脚。

师：是呀，这题在日本叫作“龟鹤算”，据史料记载，此题就源自“鸡兔同笼”。难怪有人说，近代日本之所以富强，和他们善于学习是分不开的。

（生选“春游”“投篮”“下棋”，师课件依次出示下面各题，生分别找到对应的“鸡”和“兔”）

1.要参加春游，妈妈给了我20张人民币，告诉我一共是175元，其中只有5元和10元的，我算了算，就知道5元和10元各多少张了。

2.一名篮球运动员在一场比赛中一共投中9个球，有2分球，也有3分球。已知这名运动员一共得了21分，他投中2分球和3分球各多少个？

3.学校有象棋、跳棋共26副，恰好供120个学生同时活动，象棋2人下一副，跳棋6人下一副，那么象棋、跳棋各几副？

师：看来这鸡和兔可以死心了，不管怎么变化，都躲不过你们的“火眼金睛”。你们怎么这么厉害呢？

生：我发现鸡的脚数可以变，兔的脚数也可以变，但不变的是“鸡和兔的总只数”一直是告诉我们的，虽然数可能在变化。

师：真了不起，你都发现这些变化中的共同特征了，难怪这么厉害！如果要求同时满足三个条件该怎么办？

（课件出示“百鸡问题”：今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。凡百钱买鸡百只，问鸡翁、母、雏各几何）

师：这也是一道历史名题，能用今天的收获解决新的问题吗？下课后欢迎你试一试。

（作者单位：江苏启东实验小学开发区分校）