周期复合板的带隙特性和辐射噪声衰减特性分析

徐 青， 张俊杰

(1.中国舰船研究设计中心，武汉 430064； 2.船舶振动噪声重点实验室，武汉 430064)

周期复合板的带隙特性和辐射噪声衰减特性分析

徐 青1， 张俊杰2

(1.中国舰船研究设计中心，武汉 430064； 2.船舶振动噪声重点实验室，武汉 430064)

对周期复合板的带隙特性和辐射噪声衰减特性进行了研究。运用传递矩阵法建立了周期复合板的运动方程，对于有限周期复合板，将复合板细化为小单元，利用各个单元之间的辐射阻抗，建立了周期复合板的辐射声功率预报模型。数值计算表明，周期复合板辐射噪声存在衰减阻带，在阻带频率范围内的辐射噪声被极大的抑制。研究了复合结构宽度和材料对阻带衰减特性的影响。

周期复合板；辐射噪声；带隙；传递矩阵

弹性波受到周期性复合材料或结构的调制，会产生弹性波带隙，并且在阻带频率范围内，振动会得到极大的衰减[1]。据此特性，可以运用周期复合材料衰减特定频率范围的振动。国内外专家学者[2-7]对于周期复合结构的振动衰减特性进行了大量研究，取得了丰富的研究成果。

上述研究成果中，一般是通过频响函数或速度传递率来评价周期复合结构的带隙衰减特性。当周期复合结构处于声场介质中时，会向介质中辐射噪声，从人主观感受和声信号探测角度来说，用辐射噪声来评价周期结构对振动噪声的控制效果更有意义。Shen给出了周期结构内外场声压的分布图，但没有对其机理进行深入分析。从表征整个声场特性来说，运用辐射声功率表征更有意义。为此，本文对周期复合板的带隙特性和辐射噪声的衰减特性进行研究，分析周期复合板的参数对辐射噪声衰减特性的影响。

1 理论建模

1.1 周期复合板耦合方程建模

(1) 对边简支的无限周期复合板[8]

材料A和B沿着x方向交叉排列组成的无限周期复合板如图1所示，其中周期复合板在y=0和y=Ly为简支边界条件。设材料A和B在一个周期中的长度分别为a和b，y方向的长度为Ly。

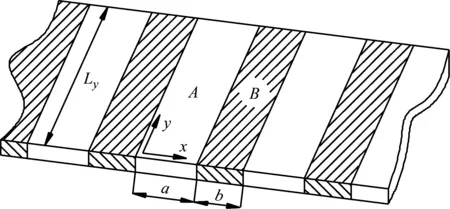
图1 无限周期复合板

采用薄板理论分别建立A材料和B材料板的运动控制方程，

(1)

(2)

式中，νi为材料的泊松比。

简谐振动下，频率为ω时方程(1)的解可以表示为

(3)

当ω<(nπ/Ly)2(Di/ρihi)1/2时，k1i和k2i均为实数，板中的波均为近场衰减波；ω>(nπ/Ly)2(Di/ρihi)1/2时，k1i为实数，k2i为纯虚数，板中才有传播波。由式(2)和式(3)，可以得到

(4)

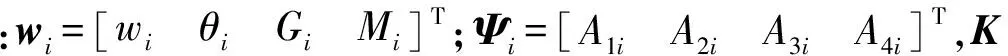
在第m-1个单元内A材料和B材料，以及第m-1个单元B材料和第m个单元A材料的交界面处，根据位移相等、转角连续、有效剪力和弯矩相等得到如下方程

(5)

由此得到递推关系式和传递矩阵T的表达式为

(6)

根据Bloch定理，建立周期结构在x方向一个周期内待定系数的关系表达式如下：

(7)

(2) 对边简支的有限周期复合板

对于一对边简支、一对边自由的有限周期复合板如图2所示，设周期数为N，设激励力作用于第m个周期的材料A,B交界处，以激励点所在的x坐标为分界线，把周期复合板分为左、右两部分，利用式(6)可建立待定系数之间的关系

(8)

式中，Ti是第i个周期单元的传递函数。

图2 有限周期复合板

根据激励点处的位移连续和力平衡边界条件w0、左右两端的边界条件w1、wN建立如下关系：

(9)

式中，L是元素为0或1的系数矩阵。组合得到

(10)

式中：Φ=[ΨA,1,ΨB,N]；L8×8是矩阵；R8×1外力构成的向量。求解式(10)得到

(11)

1.2 外部激励力

对于有限周期复合板，设外力为点激励力，沿着板宽度方向展开，根据三角函数正交性得到：

(12)

式中，F0和y0分别是激励力的幅值和位置。

对于每一简谐波n，把式(12)代入式(11)求出Φ，根据式(8)求得任意周期的待定系数ΨA,m和ΨB,m，进一步根据式(3)求出周期复合板任意点的位移。对所有的简谐波n进行叠加可获得有限周期复合板任意点的位移。

1.3 辐射声功率

采用辐射声功率评价有限周期复合板的辐射噪声控制效果。分析周期复合板在空气中的声辐射，不考虑空气介质和板的声固耦合。通过把板分成小单元，运用各个单元之间的辐射阻抗，得到整个板的辐射声功率：

(13)

式中，V是求得的有限周期复合板的速度响应；

声功率级为

(14)

式中，W0=10-12(W)。

2 数值分析

研究周期复合板的材料和几何参数对辐射噪声带隙衰减频率的影响。其中材料A(钢材)杨氏模量EA=2.1×1011N/m2，νA=0.3，密度ρA=7 850 kg/m3；材料B(橡胶)杨氏模量EB=2.1×109N/m2，νB=0.48，密度ρB=1 200 kg/m3；板的厚度为h=0.01 m；外部激励力F0=1 N，激励位置y0=Ly/6。周期复合板的几何参数不特殊说明为a=0.5 m，b=0.2 m，Ly=0.6 m。

2.1 周期复合板的辐射噪声

运用文献[9]的方法确保辐射声功率收敛的情况下，计算了由材料A和材料B组成的无限周期复合板的带隙特征，以及有限周期复合板在单位点激励(此时参与模态包括n=1，n=2和n=3)时的辐射声功率，如图3所示，由图可知：

(1) 对于无限周期复合板，由式(7)可知，特征值为4个，分别为2种向左、向右传播弯曲波。这2种弯曲波中，一种对应弯曲波的传播波，另一种对应弯曲波的近场衰减波。其中，传播波会表现出通带和阻带的特性；近场衰减波表现为整个频率范围内的很高的衰减因子，即整个频率范围内都是阻带。而弯曲波在复合材料板结构中能否传播取决于这两种弯曲波阻带的交集。由于近场衰减波在整个频段内均为阻带，传播波的阻带范围即两种波的阻带范围的交集，为此图中仅给出传播波。

(2) 由式(3)可知，每阶模态低频段有一截止频率，这段频率内，波传播被衰减，这是由于频率满足ω>(nπ/Ly)2(Di/ρihi)1/2时，复合材料板A，B中才存在传播波。由于振动响应是所有的简谐波数n叠加的结果，因此只有当所有的简谐波n都表现出阻带时，才是周期复合板的阻带，即图3所示加粗实线区域为n=1，n=2和n=3的阻带叠加区域。在阻带范围内，周期复合板的辐射声功率被极大的抑制。利用此特性，可以设计周期复合板来衰减特定频段的辐射噪声。

图4给出了周期复合板和均匀板(由材料A组成)辐射声功率的对比图，在阻带频率范围，均匀板的辐射声功率线谱被极大抑制，离散线谱幅值显著降低，因此周期复合板在阻带频率范围内能够降低辐射声功率。

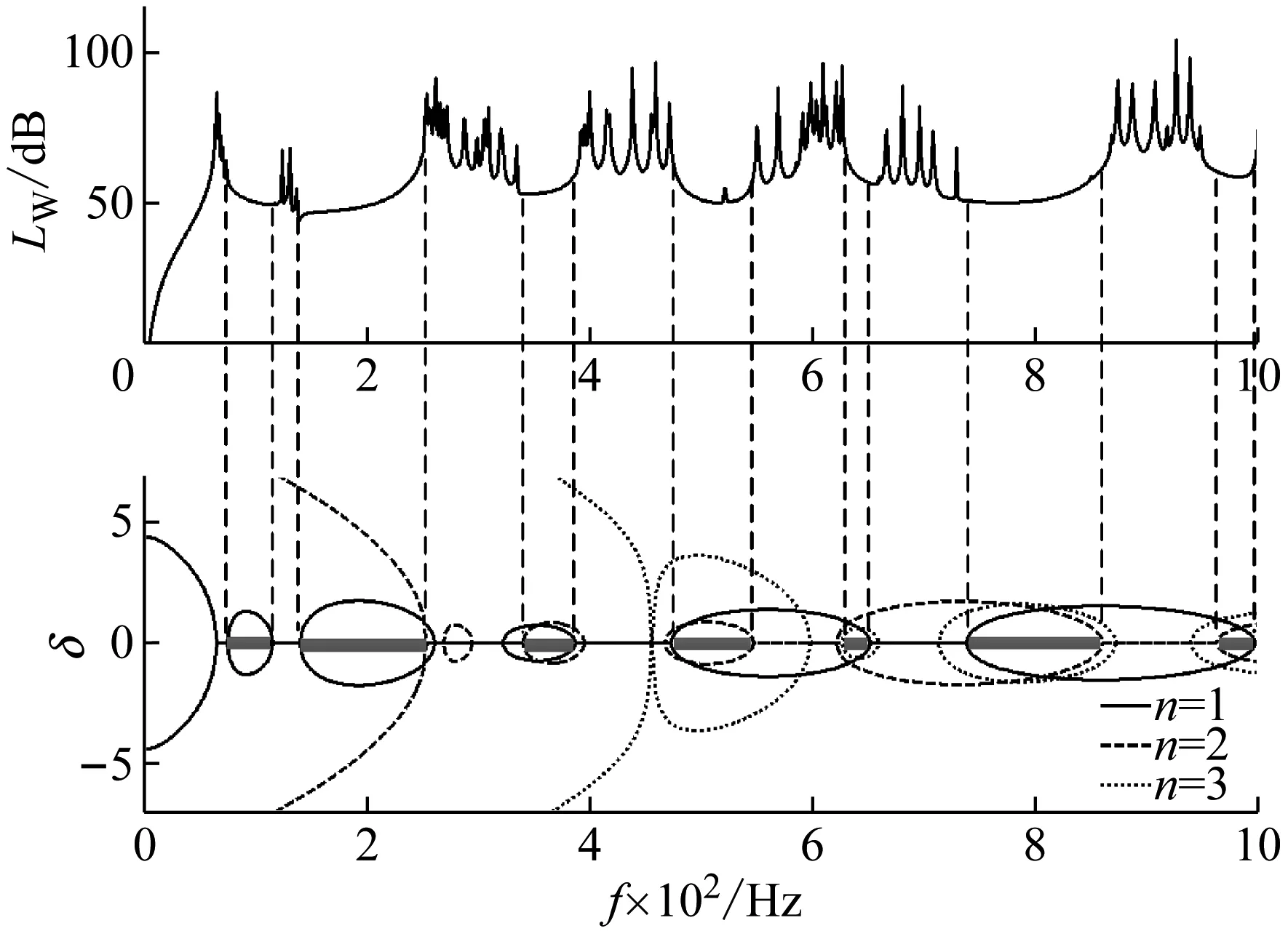
图3 周期复合板辐射噪声

图4 周期复合板辐射噪声控制效果

2.2 周期复合板材料和几何参数对辐射噪声带隙衰减频率的影响

周期复合结构的阻带频率与周期复合板的几何和材料参数相关，针对不同频段的辐射噪声控制要求，可设计出能衰减相应频段的周期复合板结构。下面对影响周期复合结构阻带频率范围的因素进行分析。

2.2.1 周期复合板的宽度

图5、图3和图6分别给出周期复合板宽度为Ly=0.4m、Ly=0.6 m和Ly=0.8 m时的辐射声功率和带隙频率分布。由图可知，随着宽度的增加，板结构的横向刚度减小，参与振动的模态数增加。由于周期复合结构的阻带频率是参与振动各个模态阻带频率的交集，因此宽度增加后周期复合板阻带频率范围总体趋势上会变窄。

2.2.2 周期复合板的材料参数

将材料B变更为环氧树脂(ρB=1 180 kg/m3、EB=4.35×109N/m2、νB=0.37)和铝(ρD=2 730 kg/m3、ED=7.76×1010N/m2、νD=0.35)，得到的辐射声功率和带隙频率分布分别如图7和图8所示。通过与图3对比可知，周期复合板的两种材料参数差异越大，辐射噪声的阻带频率范围越宽，也即越容易产生辐射噪声阻带。但是从周期复合结构承载功能角度来说，两者材料参数不能相差太大，因此需要综合考虑周期复合结构功能和声学性能，以设计出满足需求的周期复合结构。

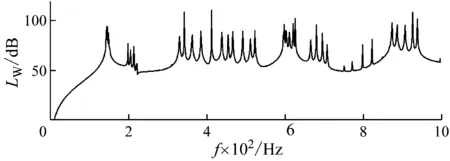
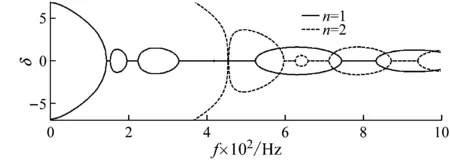
图5 周期复合板宽度

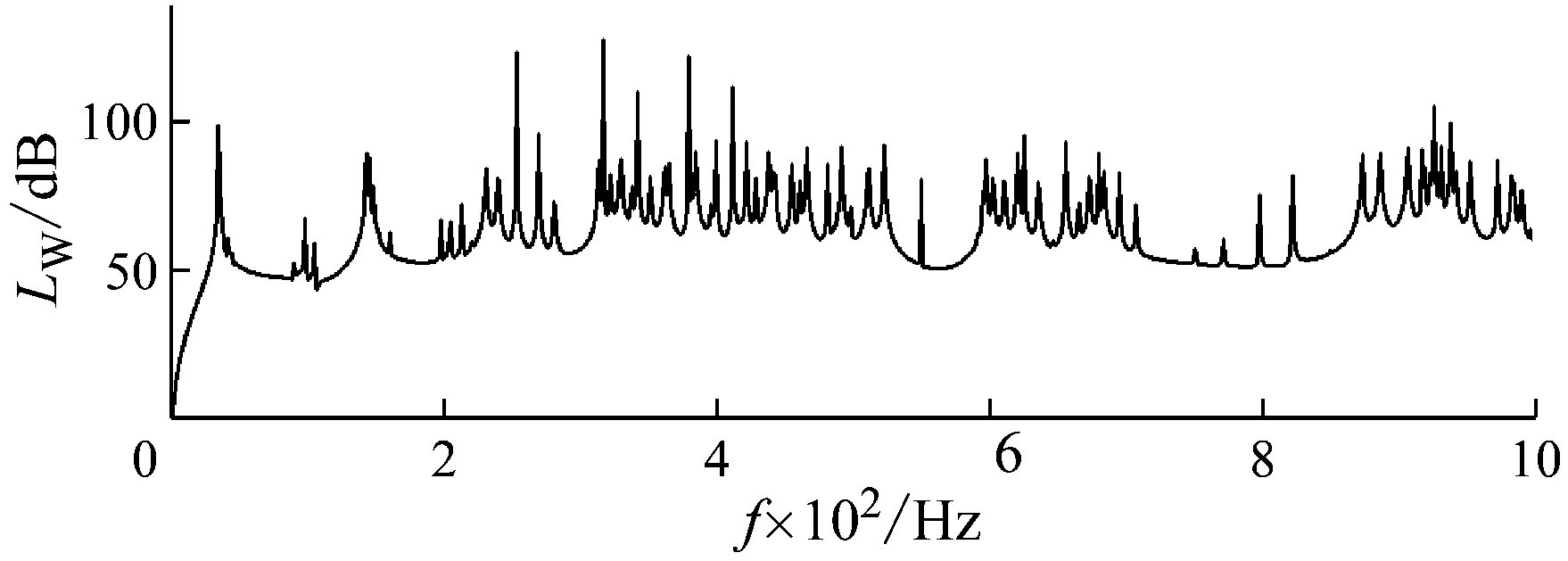
图6 周期复合板宽度Ly=0.8 m

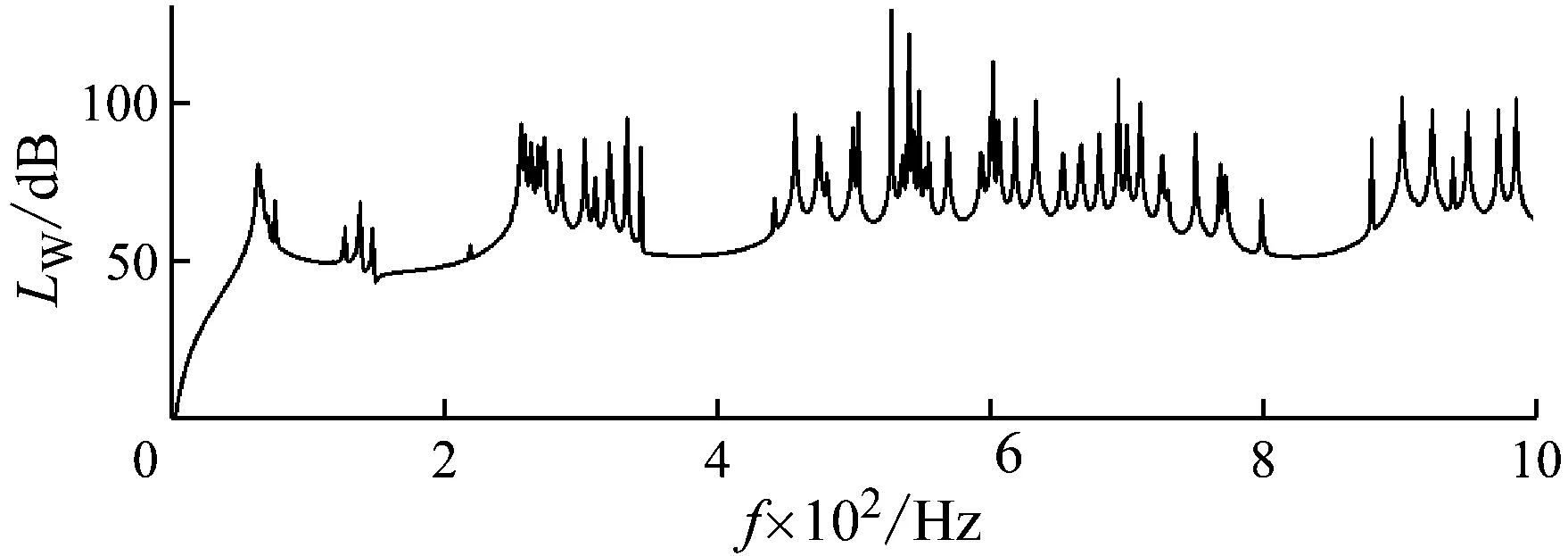
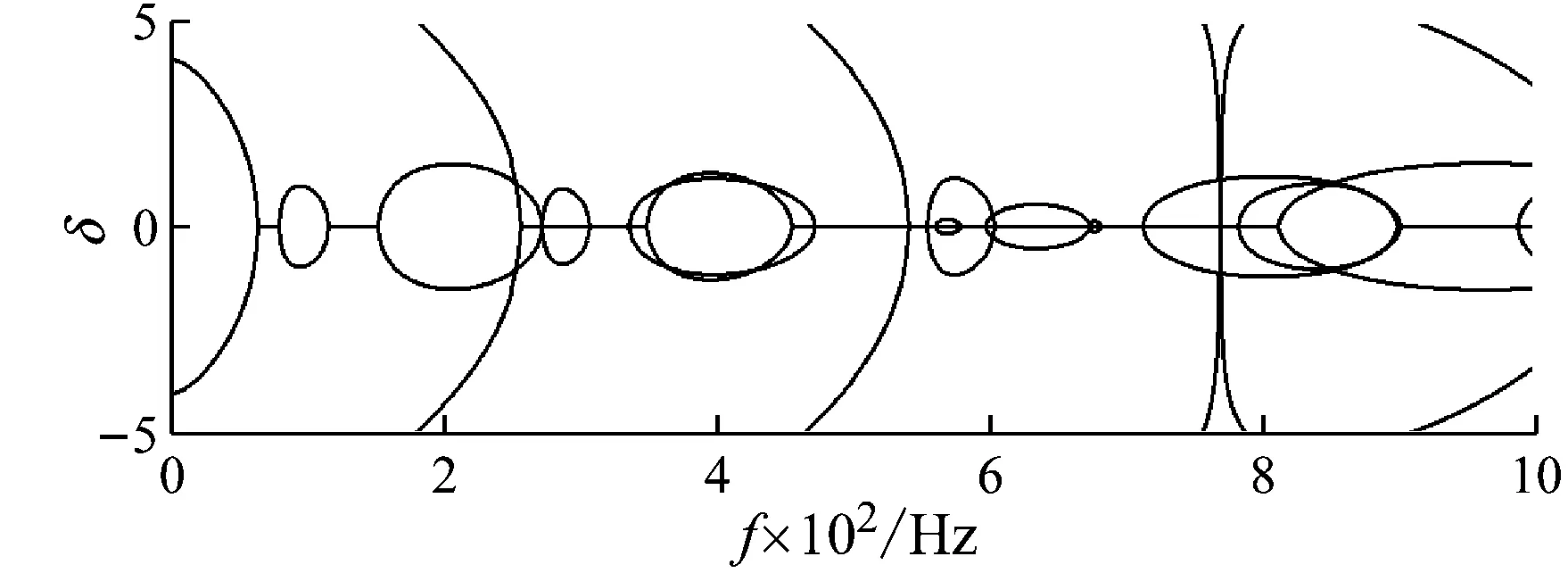
图7 材料B改为环氧树脂的辐射声功率

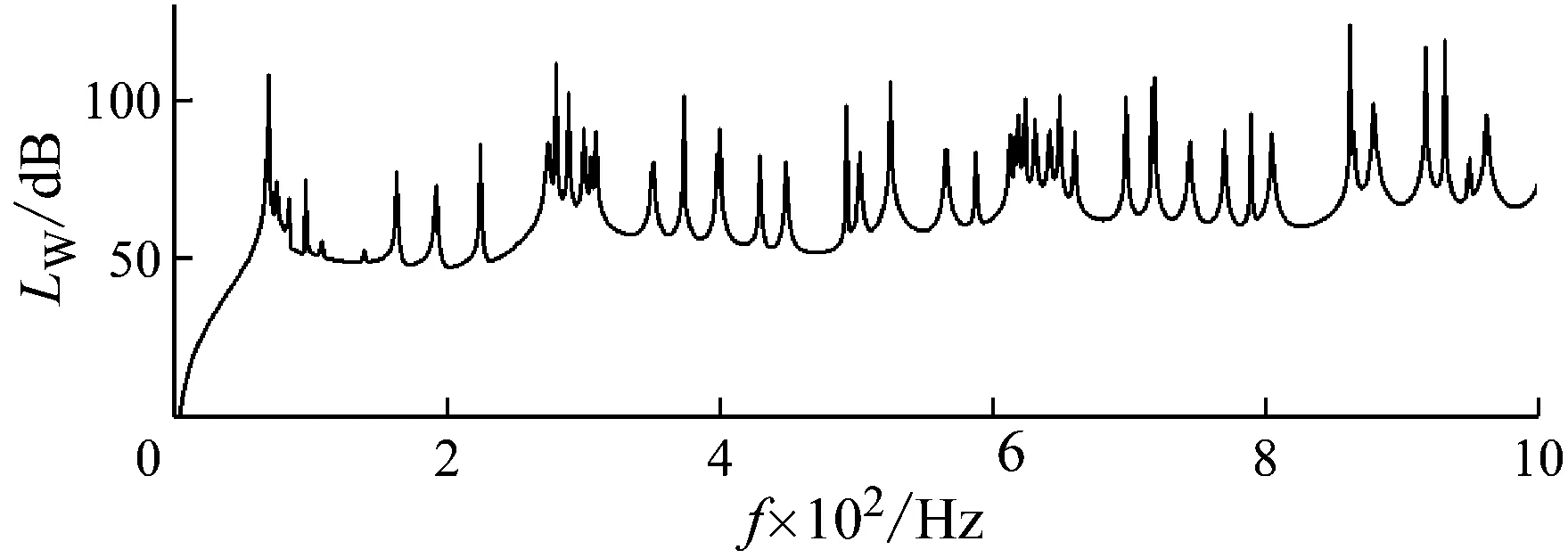
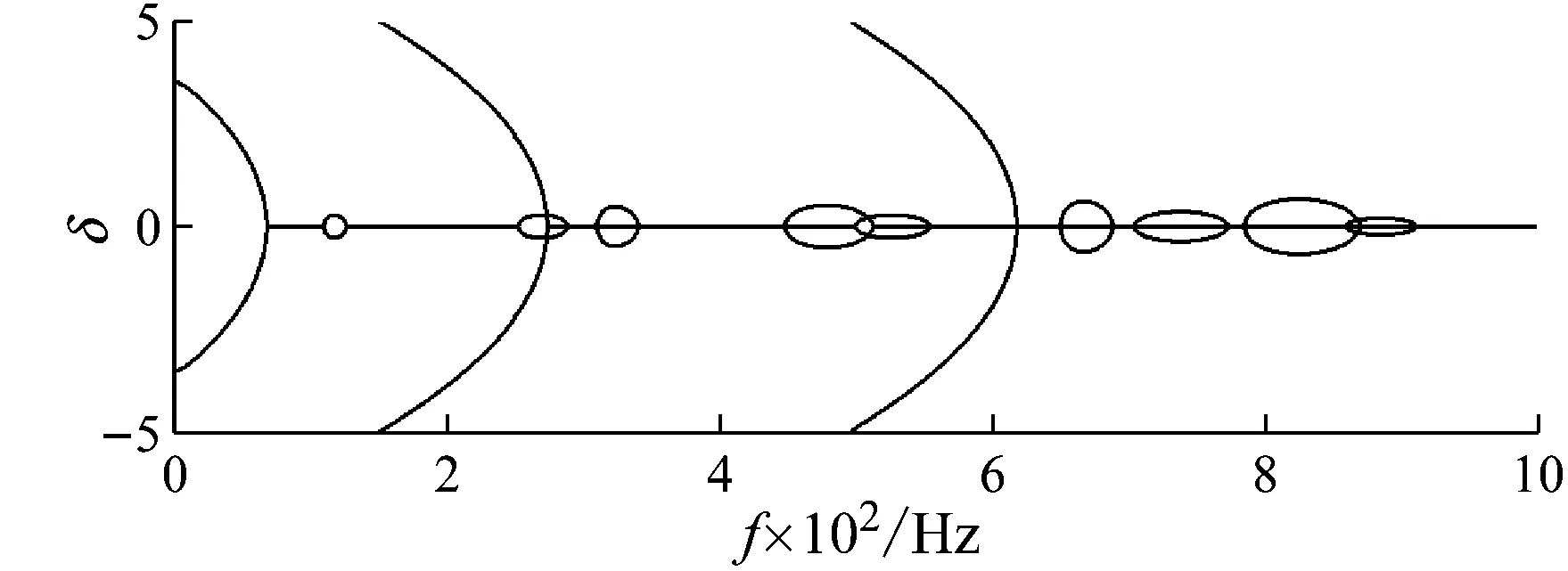
图8 材料B改为铝的辐射声功率

3 结 论

(1) 周期复合板结构存在辐射噪声带隙频段，在带隙频率范围内，周期复合板的辐射噪声得到极大抑制；

(2) 随着周期复合板结构宽度增加，参与振动的模态数增加，周期复合板带隙频率范围总体上变窄；

(3) 周期复合板结构材料参数差异越大，越容易产生辐射噪声带隙。

[1] 郁殿龙．基于声子晶体理论的梁板类周期结构振动带隙特性研究[D]. 长沙：国防科学技术大学，2006.

[2] 肖伟．声子晶体型周期复合结构禁带特性研究[D]. 武汉：华中科技大学，2007.

[3] SOROKIN S V, ERSHOVA O A. Analysis of the energy transmission in compound cylindrical shells with and without internal heavy fluid loading by boundary integral equations and by Floquet theory[J]. Journal of Sound and Vibration, 2006, 291(1/2): 81-99.

[4] SHEN Huijie, WEN Jihong, PAÏDOUSSIS M P, et al. Control of sound and vibration for cylindrical shells by utilizing a periodic structure of functionally graded material[J]. Physics Letters A, 2012, 376(1/2): 3351-3358.

[5] SHEN Huijie, WEN Jihong, YU Dianlong, et al. Control of sound and radiation of fluid-filled cylindrical shells via periodic design and active control[J]. Journal of Sound and Vibration, 2013,332(18): 4193-4209.

[6] 张思文，吴九汇，刘彰宜．黏弹阻尼对一维杆状声子晶体能带结构频移的影响[J].西安交通大学学报，2014，48(3)：22-27.

ZHANG Siwen, WU Jiuhui, LIU Zhangyi. Damping-induced frequency shifts in band structures of one-dimensional viscoelastic phononic crystal rods[J]. Journal of Xi’an Jiaotong University, 2014, 48(3): 22-27.

[7] 陈启勇，胡少伟，张子明．基于声子晶体理论的弹性地基梁的振动特性研究[J].应用数学和力学，2014,35(1)：29-38.

CHEN Qiyong, HU Shaowei, ZHANG Ziming. Research on the vibration property of the beam on elastic foundation based on the PCs theory[J]. Applied Mathematics and Mechanics, 2014, 35(1): 29-38.

[8] 张俊杰．基于波传播法的周期复合板振动带隙衰减特性研究[J]，物理学报，2014，63(22)：224302(1-8).

ZHANG Junjie. Band gap attenuation characteristics of periodic compound plate with wave propagation approach[J]. Acta Phys. Sin., 2014, 63(22): 224302(1-8).

[9] 张俊杰，原春晖，刘彦，等．基于解析解和边界元解的圆柱壳声辐射对比研究[J].振动与冲击，2013，32(4)：1-5.

ZHANG Junjie, YUAN Chunhui, LIU Yan, eta. Sound radiation result comparison for a cylindrical shell based on analytical solution and boundary element method[J]. Journal of Vibration and Shock, 2013, 32(4): 1-5.

Research on the band gap and attenuation characteristic of sound radiation for periodic compound plate

XU Qing1, ZHANG Junjie2

(1. China Ship Development and Design Center, Wuhan 430064, China; 2. National Key Laboratory on Ship Vibration & Noise, Wuhan 430064, China)

The band gap and attenuation characteristics of sound radiation for periodic compound plate were investigated. The coupled equations were established by transfer matrix method, and radiation sound was calculated by radiation impedance through meshing the plate into equal squares. Calculations showed that there are stop bands for the radiation sound, and the level of sound radiation is greatly suppressed in the frequency ranges of the stop bands. The influence of the material and geometric parameters on band gap was discussed.

periodic compound plate; radiation sound; band gap; transfer matrix

国家自然科学基金(51409238;61503354)

2016-03-08 修改稿收到日期：2016-07-12

徐青 男，研究员，1960年生

TB535

A

10.13465/j.cnki.jvs.2017.11.030