斜拉索风雨激振数值模拟及其机理探究
2017-06-19毕继红
毕继红, 武 骥, 关 健, 王 剑
(1. 天津大学 建筑工程学院, 天津 300072; 2. 滨海土木工程结构与安全教育部重点实验室, 天津 300072;3. 天津城建大学 土木工程学院, 天津 300384; 4. 天津软土特性与工程环境重点实验室, 天津 300384)
斜拉索风雨激振数值模拟及其机理探究
毕继红1,2, 武 骥1, 关 健1, 王 剑3,4
(1. 天津大学 建筑工程学院, 天津 300072; 2. 滨海土木工程结构与安全教育部重点实验室, 天津 300072;3. 天津城建大学 土木工程学院, 天津 300384; 4. 天津软土特性与工程环境重点实验室, 天津 300384)
将滑移理论与CFD技术相结合,考虑了风压力系数和风摩擦因数随位置和时间的变化,并引入了Spalart-Allmaras(S-A)湍流模型,运用有限单元法,实现了对斜拉索的风雨激振现象的数值模拟;考察了不同风速下的水线形成及形态,并与已有实验成果进行比对,验证了方法的合理性和准确性;研究了水膜形态、气动力变化、斜拉索振动响应三者关系,得到了水线和拉索之间的振动耦合规律,探讨了风雨激振机理。结果表明,水线、气流和斜拉索之间的共振是引发风雨激振的主要因素之一。
风雨激振; 水线; 气动力; 斜拉索振动
风雨激振是指在风雨共同作用下,斜拉索发生的低频、大幅度振动,危害极大。对此,研究人员运用现场实测、风洞试验、理论分析方法对此进行了大量研究。然而,各国内外学者对其产生机理并未达成统一。顾明等[1]进行了斜拉索人工雨线测压试验, 建立了三维拉索,三维水线风雨激振模型,分析认为平均气动力系数的突降是致振机理。刘庆宽等[2]认为,卡门涡的脱落受到轴向流的抑制,低频涡的产生得到激励,受其影响,拉索产生涡激发散振动。Cheng 等[3]认为,在临界雷诺数状态下,尾流涡脱规律性发生变化,产生气动升力,致使拉索振动。Bi等[4]认为,影响风雨激振现象产生的重要因素是上水线的产生和其振荡。
近来,由于现场观测的随机性和不确定性,风洞实验再现风雨激振的困难性,使得运用CFD数值模拟技术分析风雨激振机理得到发展。然而,现有的CFD数值模拟方法有诸多不足,需要进一步改进。其一,个别数值模拟方法需调用多个计算软件,且各软件之间兼容性不佳,模型参数和计算结果需人工大范围处理,以致工作量极大,极易出现错误;其二,风雨激振是气、液、固三种相态相互耦合的复杂问题,因方法限制和计算精度要求,以致计算时间步长极短,计算耗时冗长。其三为简化计算,个别方法采用固定风压力和风摩擦因数,忽略了水线形态和位置变化对其的动态影响,不能完全反映水线形成的物理场景,这与实际不符。针对上述弊病,本文做如下改进:① 运用COMSOL软件建模,MATLAB计算,在风雨激振的数值模拟中将二者无缝链接,减少计算和人为错误;② 使用差分法解水膜方程,保证精度的前提下,增大计算时间步长,采用S-A湍流模型,提升计算效率;③ 克服采用固定气动力系数的弊病,采用随时间和位置变化的风压力和风摩擦因数即瞬态气动力系数,贴近风雨激振物理场景,提高准确性。在此基础上,建立了拉索风雨激振的理论模型并与已有实验进行了对比验证。分析了风雨激振条件下的水膜形态、气动力变化、斜拉索振动响应三者关系,并探究了风雨激振的产生机理。
1 模型建立
1.1 几何模型
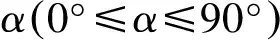

图1 斜拉索空间位置
取图1中的斜拉索A-A断面为研究对象,如图1,2所示。忽略重力沿斜拉索轴向的分量,则作用在斜拉索断面内的重力分量gN:
(1)
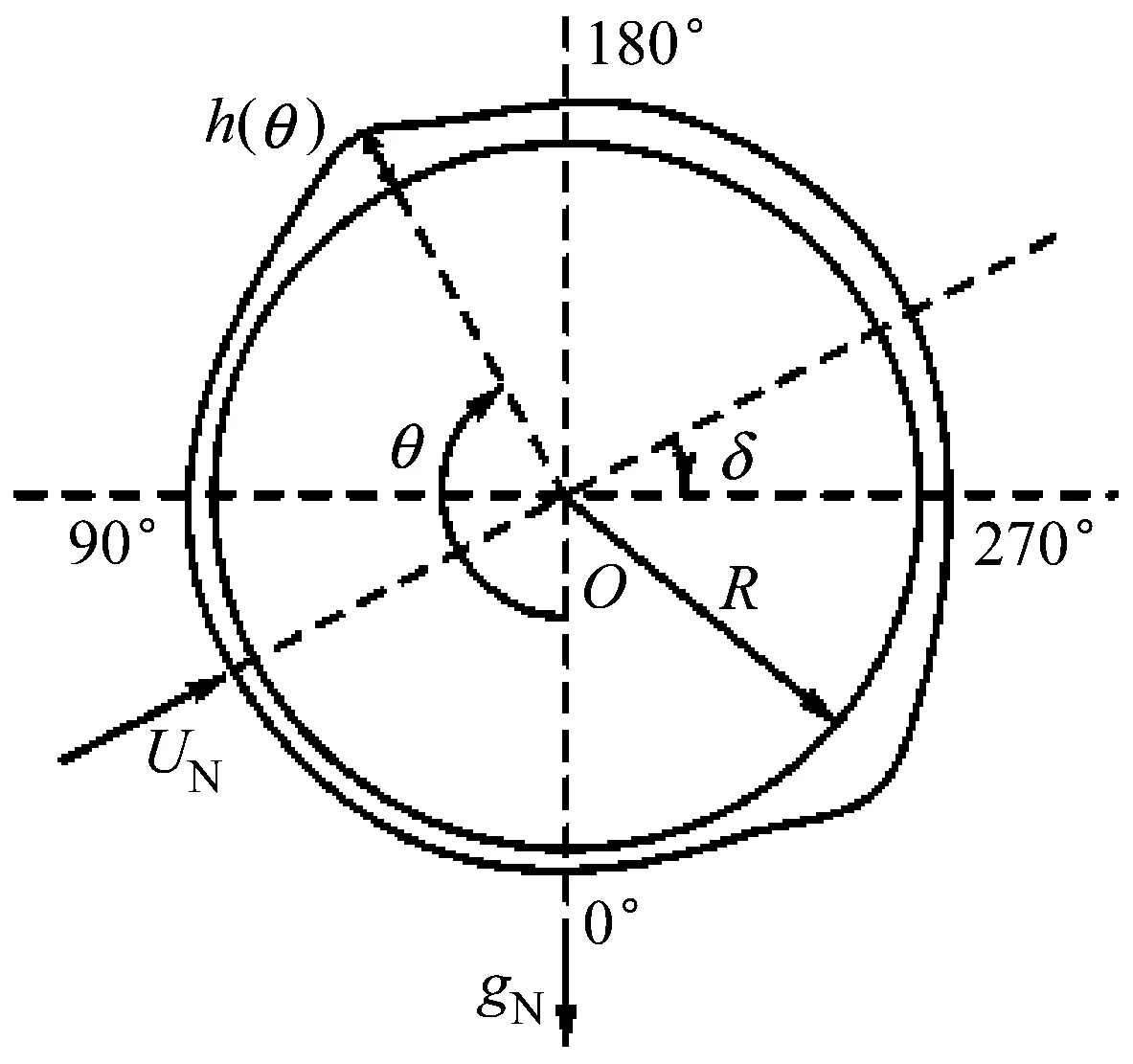
图2 斜拉索表面水膜受力
忽略轴向流的影响,只考虑垂直于斜拉索的气流作用,则斜拉索断面内的风速UN:
(2)
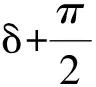

(3)
1.2 基于滑移理论的水膜运动方程
根据滑移理论,认为斜拉索表面存在水膜[5-6],采用极坐标系(er,e0)下的采用极坐标系下Navier-Stokes公式(4)~(6)描述水膜在拉索表面的运动,初始水膜厚度为h0,厚度为h(θ,t),水膜内任意一点坐标为(r,θ),其速度可表示为u=urer+uθe0。
(4)
(5)
(6)
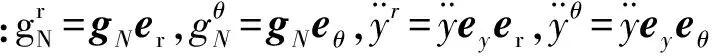
经代入边界条件,结合滑移理论进行简化,并经过无量纲化处理后,在重力、表面张力、风压力和风摩擦力下的单向耦合水膜运动方程为(7),并通过差分法进行求解;
(7)

(8)

(9)
式中:u为水膜内的流场速度;ρg和ρ分别为空气和水的密度;p为水膜内的压强;ν为水的动力黏度系数;γ为水在空气中的表面张力系数;σg为空气的应力张量;Pg为水膜表面所受的空气压力;n和t分别为水膜与空气交界处的法向向量和切向向量。其具体的无量纲化见文献[7]。
1.3 应用COMSOL技术获得风压力系数Cp和风摩擦因数Cf
此前的计算,Cp和Cf多为静态固定不变,不能准确反映拉索表面气动力的变化,以致不能准确模拟水膜水线的形成和分析风雨激振的真正机理。为弥补此缺陷,运用COMSOL软件计算随时间和空间位置动态变化的Cp和Cf,并利用MATLAB编程自动调用瞬态Cp和Cf进行计算。
选取的计算区域如图3所示,设拉索直径为D=2R,计算区域取边长为27.5D×20D的矩形,右侧为入口,左侧为出口,将拉索中心置于坐标原点,拉索中心距离入口10D,距离出口17.5D,距离上下边界10D。计算流场网格划分如图4。采用RANS(Reynolds Average Navier-Stokes)湍流数值模拟方法,进行稳态计算。采用Spalart-Allmaras湍流模型。边界条件设置如下:拉索为无滑移固壁边界;上部和下部均为滑移边界;右侧为速度入口边界,设置风场风速为UN;左侧为出口边界,边界条件为压力P=0,并且抑制回流。在保证计算结果准确性的前提下,较其他方法增大时间步长,取为dt=0.001 s,提升计算效率。
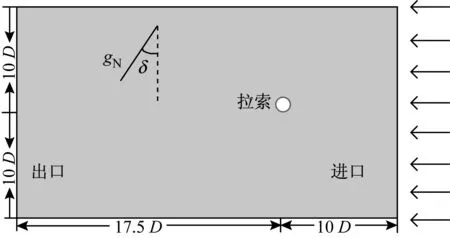
图3 流场计算区域

图4 流场网格示意图
1.4 计算参数
参照LI等[8-10]的实验工况选取模型基本参数、模型验证参数分别如表1、表2;根据斜拉桥设计规范[11]建议的斜拉索设计宜用倾角区间和常见自然环境风向,选取拉索倾角和风偏角。
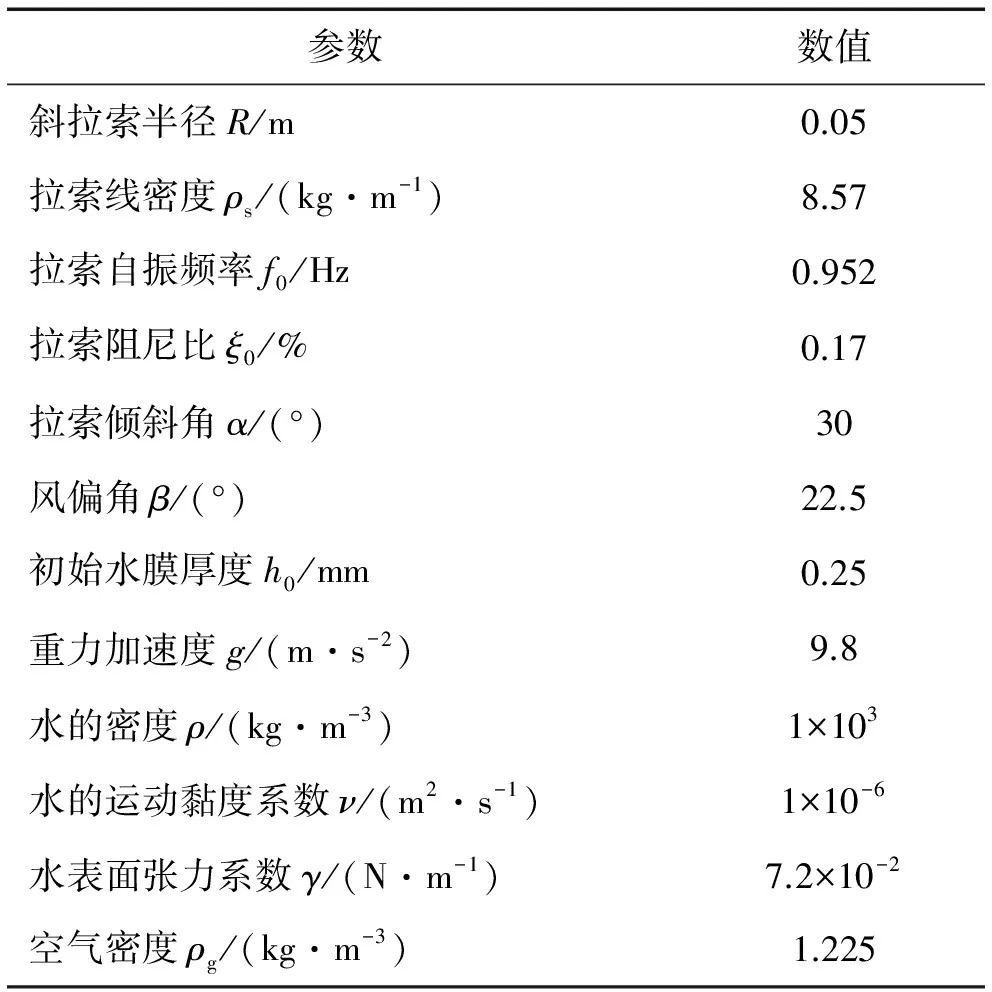
表1 模型基本参数

表2 模型验证参数
2 模型验证
本文将滑移理论与CFD技术相结合,建立有限元模型模拟水线形成。为验证此方法的可靠性和准确性,本文考察不同风速下上水线的形成,考察水线初始形成形态,并与实验数据进行比对。如图5,水线形成时间随风速增大逐渐变短,在风速小于8.04 m/s时,水线形成时间随风速增大而急剧变短;当风速大于8.04 m/s时,水线形成时间随风速增大而平缓变化,上述规律与Bi[12]所述规律相同。
如图6所示,稳定的上水线形成位置处在50.63°~ 81.56°内,与实测测数据52.48°~ 82.51°符合很好。如图7所示,上水线平均高度0.52 mm,与实验观测到的0.509 mm[10]非常接近。如图8所示,上水线平均宽度7.34 mm,亦非常接近实验观测到的水线宽度7.96 mm。说明,其一,本文模拟方法准确性高、稳定性强,由此方法推导的结论有很强的可靠性。其二,风速是上水线振荡和水膜形态变化的显著影响因素。

图5 不同风速下的水线初始形成时间
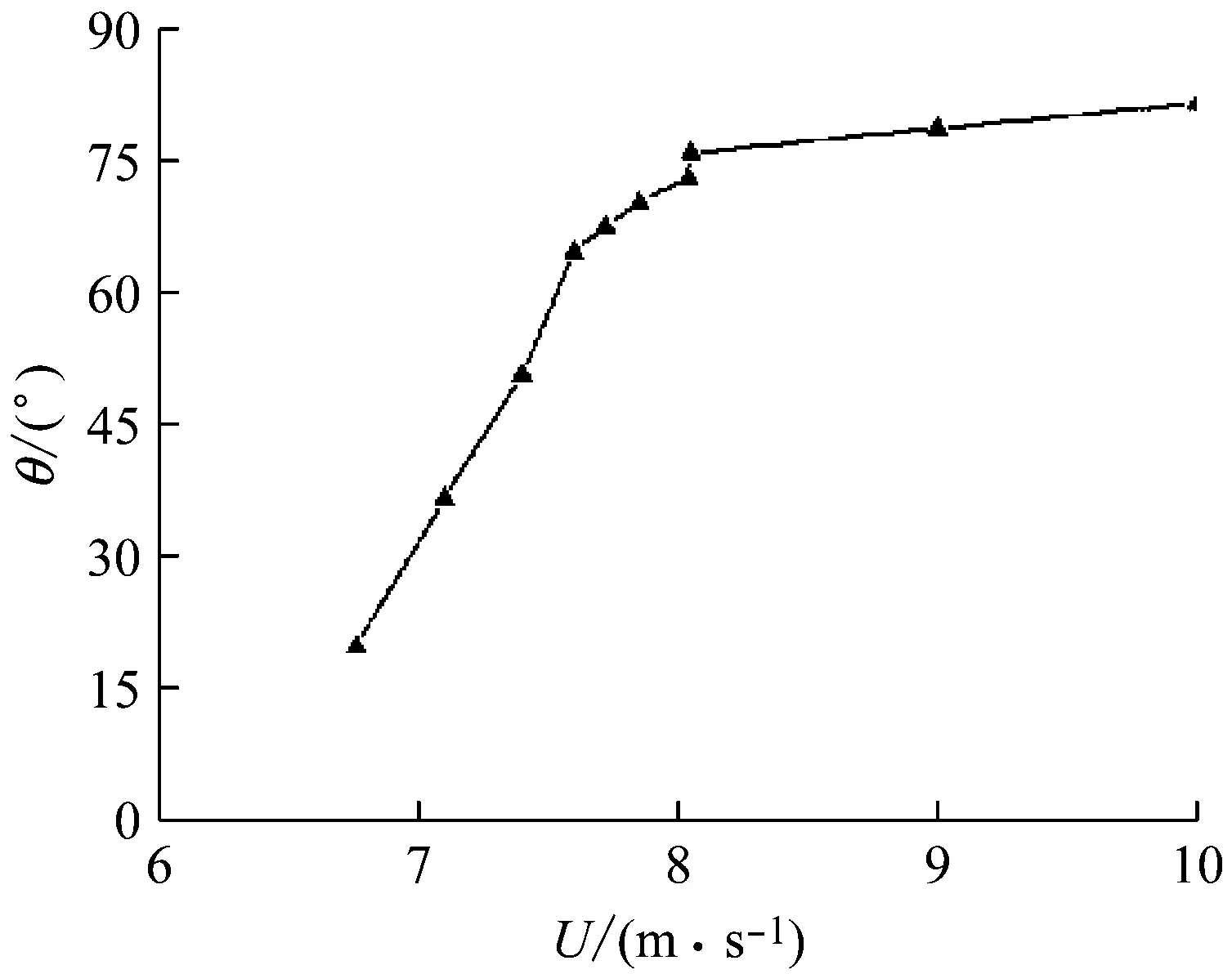
图6 不同风速下的水线初始形成位置
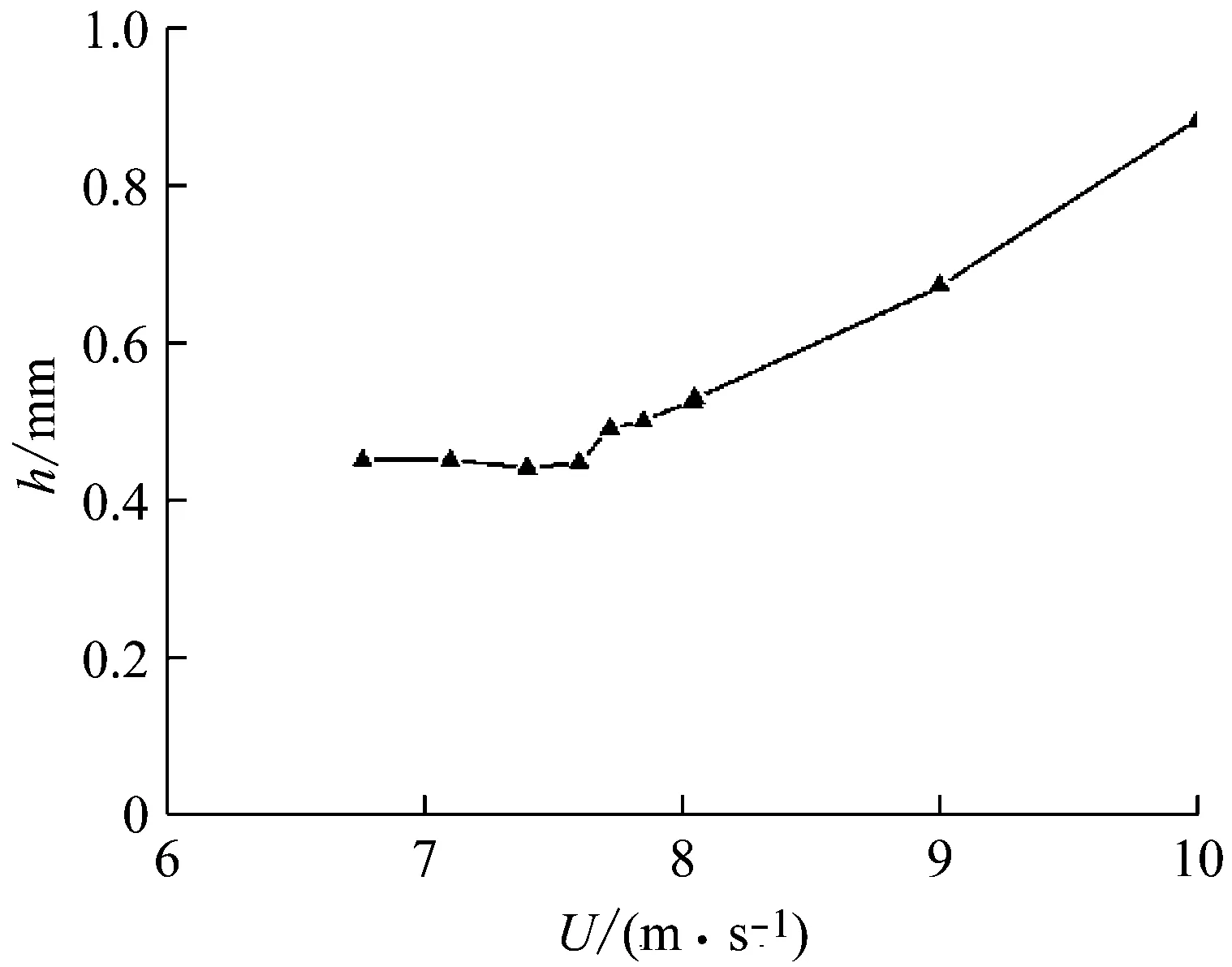
图7 不同风速下的水线高度
3 水线模拟结果分析
3.1 斜拉索表面水膜形态变化
学界普遍认为风雨激振主要受上水线的形成和振荡影响,为揭示风雨激振机理,本文选取了激振风速U0=7.72 m/s的工况,重点对上水线作了研究分析。如图9所示,t=0.27 s左右开始形成上水线,初始形成位置约为67.5°,其振荡区间大致位于55°~85°,高度约为0.49 mm,宽度约为9.64 mm。上水线宽度、高度发展较大时,由于重力,上水线产生向下滑落现象,引起水膜、水线形态变化。

图8 不同风速下的水线宽度

(a) 2D水膜形态
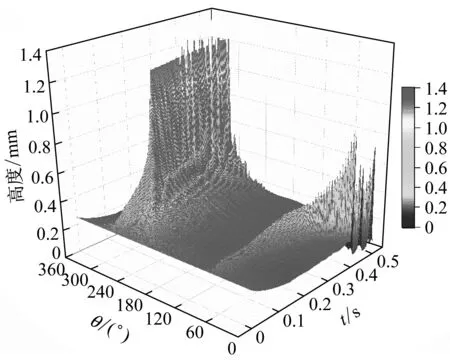
(b) 3D水膜形态
图10显示了在0°位置处,风速在U0=7.72 m/s时水膜的高度时程变化和其频谱分析。如图10(a)所示:水膜形态出现了两阶段变化:t=0 s~20 s为剧烈变化阶段,由于水线的形成、滑落剧烈,使得水线震荡、水膜厚度起伏变化幅值较大;t=20 s以后为平稳变化阶段,气流产生的风压力和风摩擦力的变化趋于平稳,水线振荡和水膜厚度变化逐渐显示了明显的规律性和稳定性。如图10所示,可以发现水膜厚度其振荡频率f≈1 Hz,与试验中与斜拉索的自振频率f0≈0.952 Hz相近。
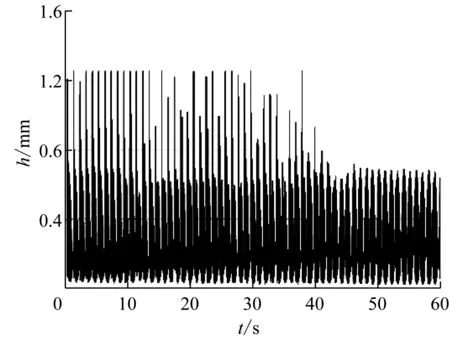
(a) 时程曲线
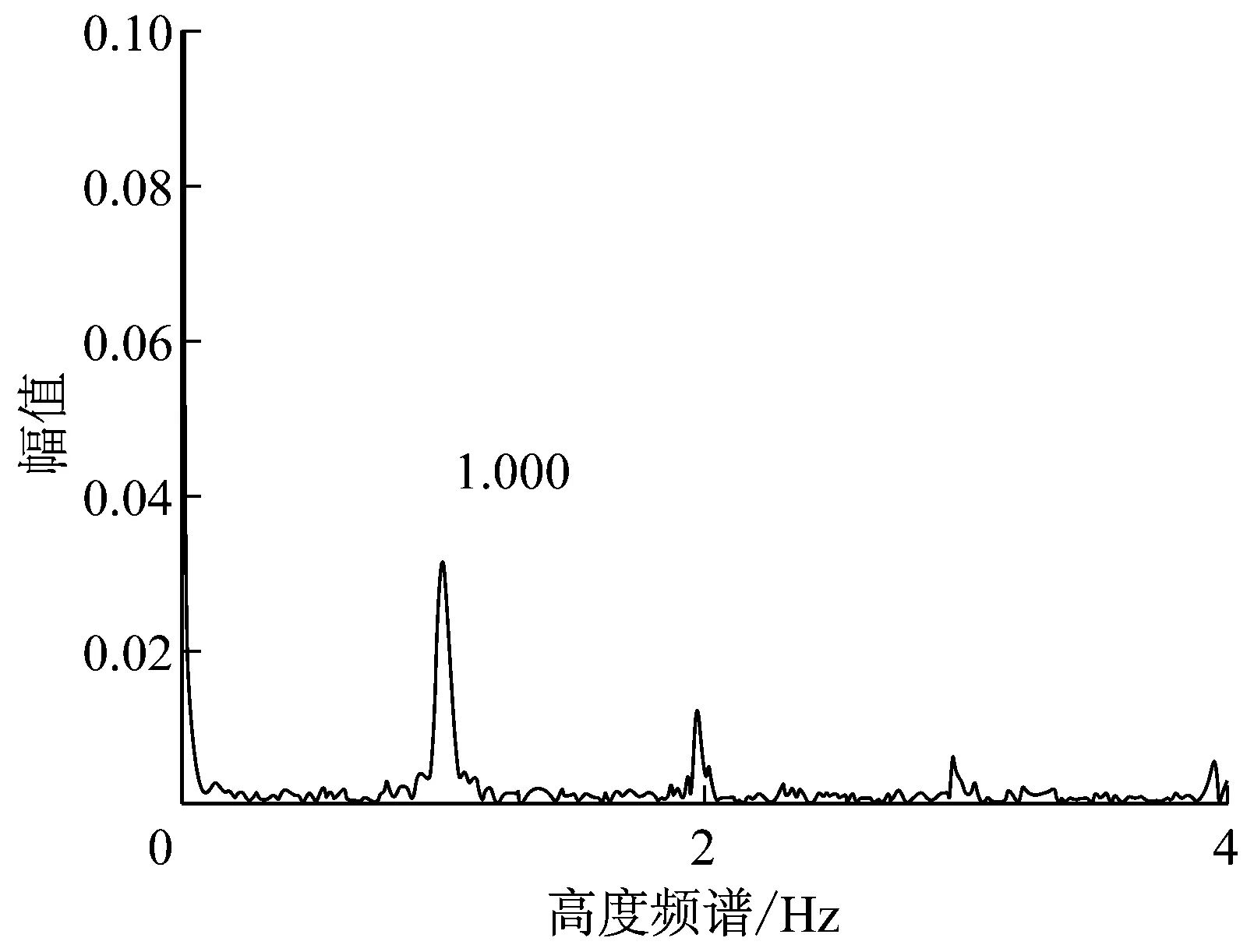
(b) 频谱分析
3.2 斜拉索表面气动力
t=60 s处于平稳变化阶段,并以此时刻为研究对象,如图11所示,风压力系数Cp、风摩擦因数Cf、表面风速、风压力等高线在50°~85°范围内发生了显著变化,这与图9显示的上水线的形成和振荡位置相吻合。这表明,气动力的突变区域位于上水线的振荡区域,分析得知,上水线的振荡对Cp、Cf有重大影响,受到影响的气动力又反作用于水膜形态,同时影响拉索振动,各因素相互作用,密切联系。进一步说明考虑Cp、Cf随时间和位置的变化对准确模拟风雨激振的必要性和重要性。
图12(a), 13(a)显示了U0=7.72 m/s时采用固定Cp、Cf时的气动力变化:气动升力波动区间为-0.9 N~-0.4 N,气动阻力波动区间为5.0 N~5.2 N,与采用瞬态Cp、Cf时的气动力相比,振幅明显偏小。这表明是否采用瞬态Cp、Cf进行计算,对气动力的计算结果影响很大,进而很大程度上影响风雨激振数值模拟的准确性。
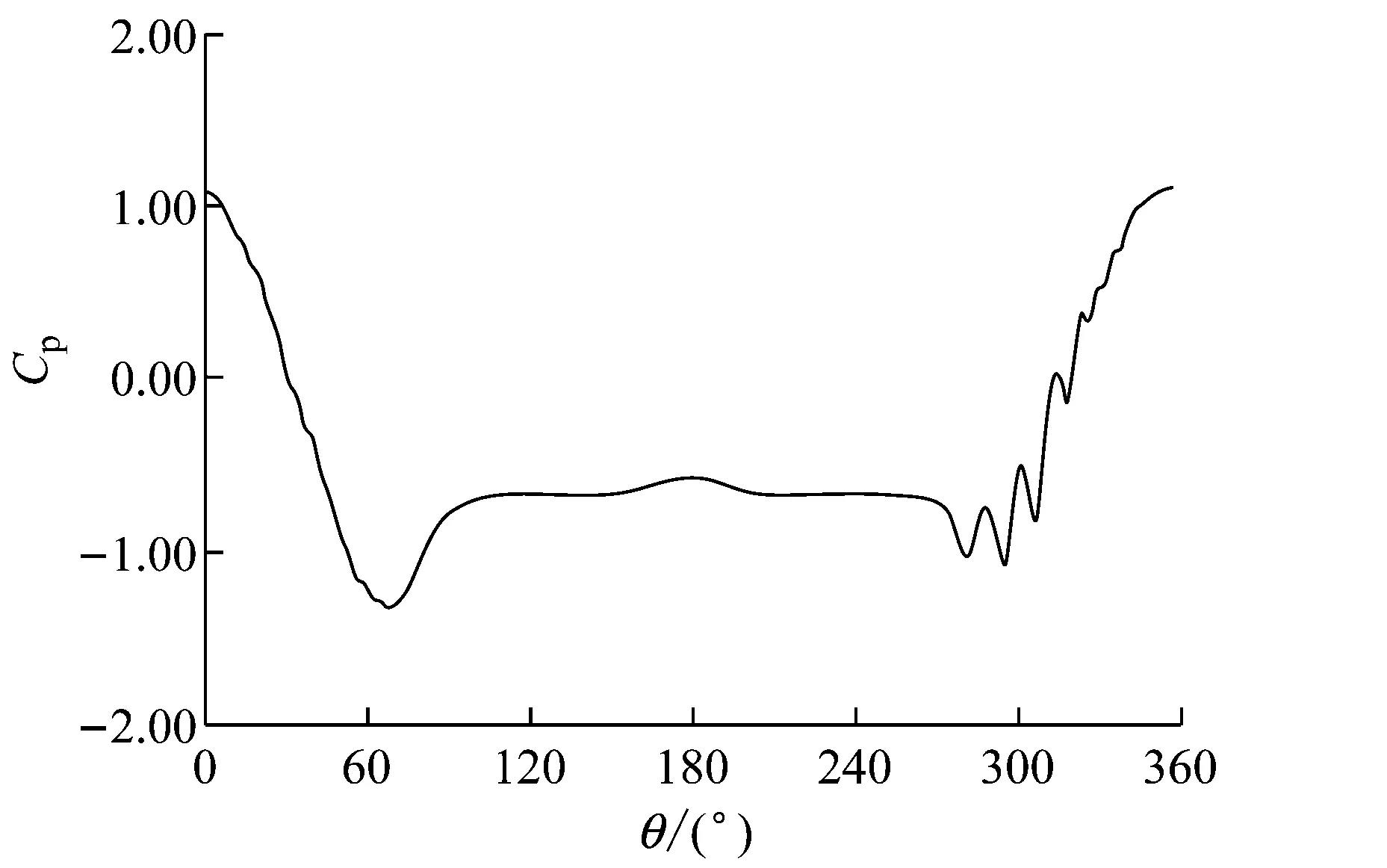
(a) 风压力系数Cp
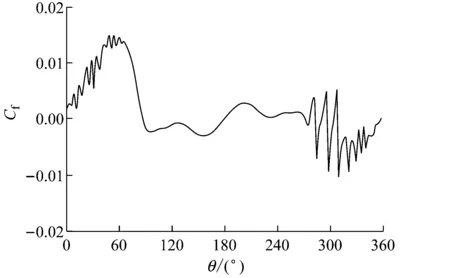
(b) 风摩擦因数Cf
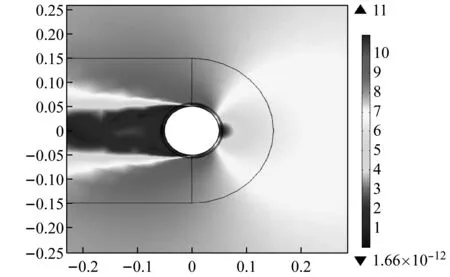
(c) 表面风速随位置变化图示(m/s)
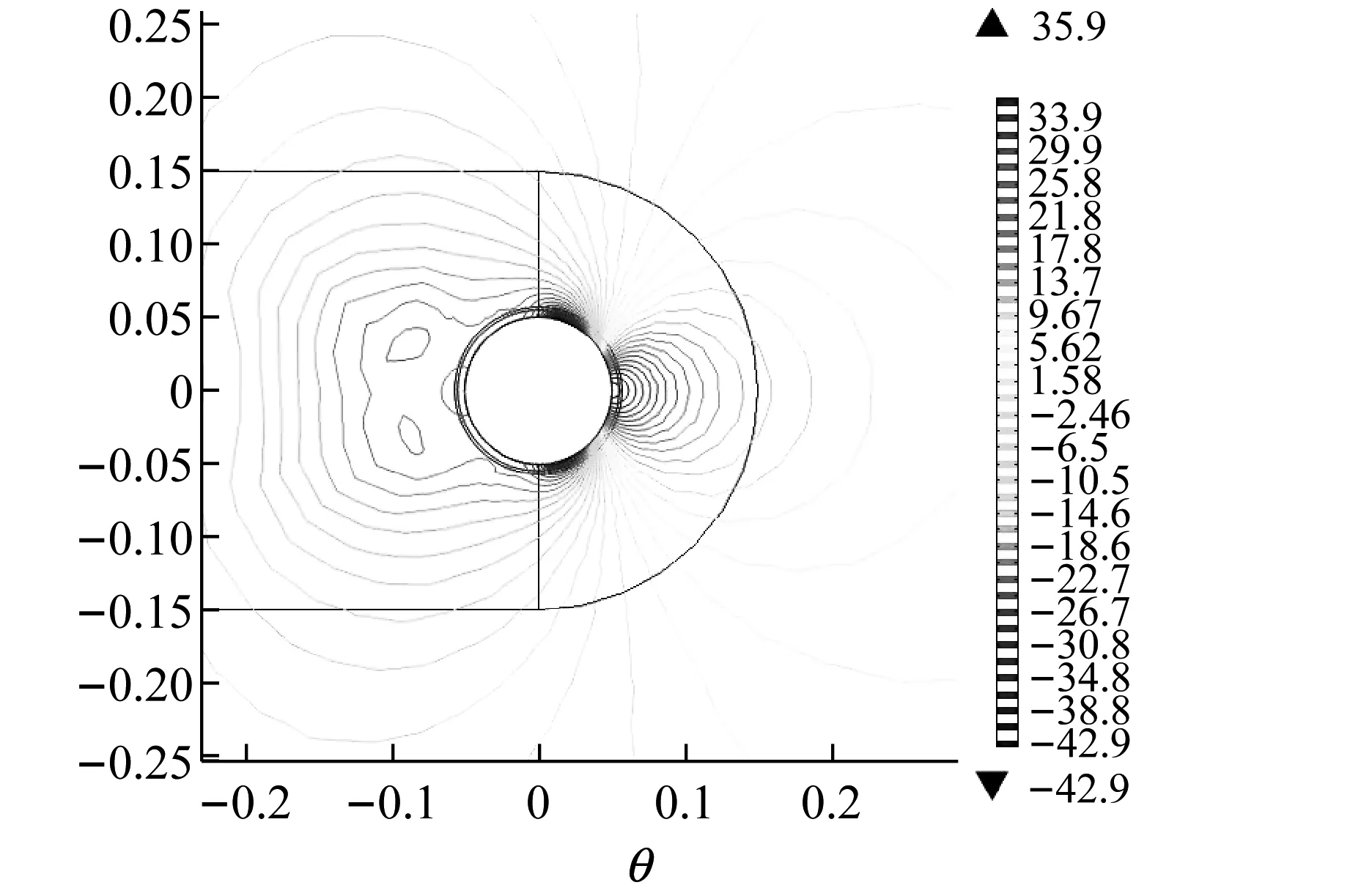
(d) 气动力等高线随位置变化图示(Pa)
图12(b),13(b)显示了U0=7.72 m/s时的采用瞬态Cp、Cf斜拉索气动力变化。如图所示,气动力时程显示了与水膜形态变化一致的阶段性:t=0 s~20 s为剧烈变化阶段,气动升力从-0.4 N~0.8 N快速变大为-0.6 N~1.0 N,气动阻力从4.7 N~6.5 N快速降为5 N~6.3 N。t=20 s以后为平稳变化阶段,气动力逐步稳定,并且升力幅值处在-0.6 N~1.2 N之间,阻力气动力幅值处在5.2 N~5.8 N之间,变化稳定,周期性明显。分析认为,最初,水膜形态在初始风速的作用下剧烈变化,导致气动力幅值剧烈变化;此后,水膜形态变化和气动力变化相互耦合,使得较初始状态变化更为缓和;最后,水线的振荡和水膜形态逐渐趋于稳定,导致气动力变化逐渐趋于稳定,稳定变化的气动力又反过来作用于水线,保证水膜形态的稳定变化,各因素相互作用、相互协调,达到平衡,协同保证了此现象的稳定性和规律性。
如图12(c)和图13(c)所示:升力和阻力的振荡频率分别为fy≈1 Hz和fx≈1 Hz,与LI等[8-10]的实验结果相近。气动力振荡频率与0°处的水膜厚度振荡频率相同再一次证明,气动力的周期性振荡与水膜形态周期性变化密切相关。
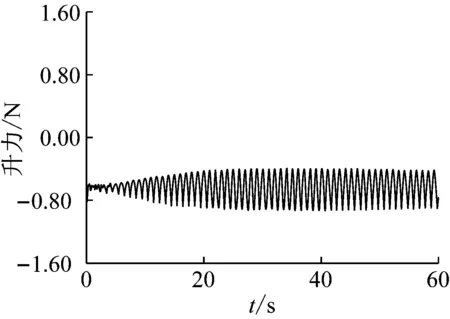
(a) 升力时程曲线(固定Cp、Cf)

(b) 升力时程曲线(瞬态Cp、Cf)
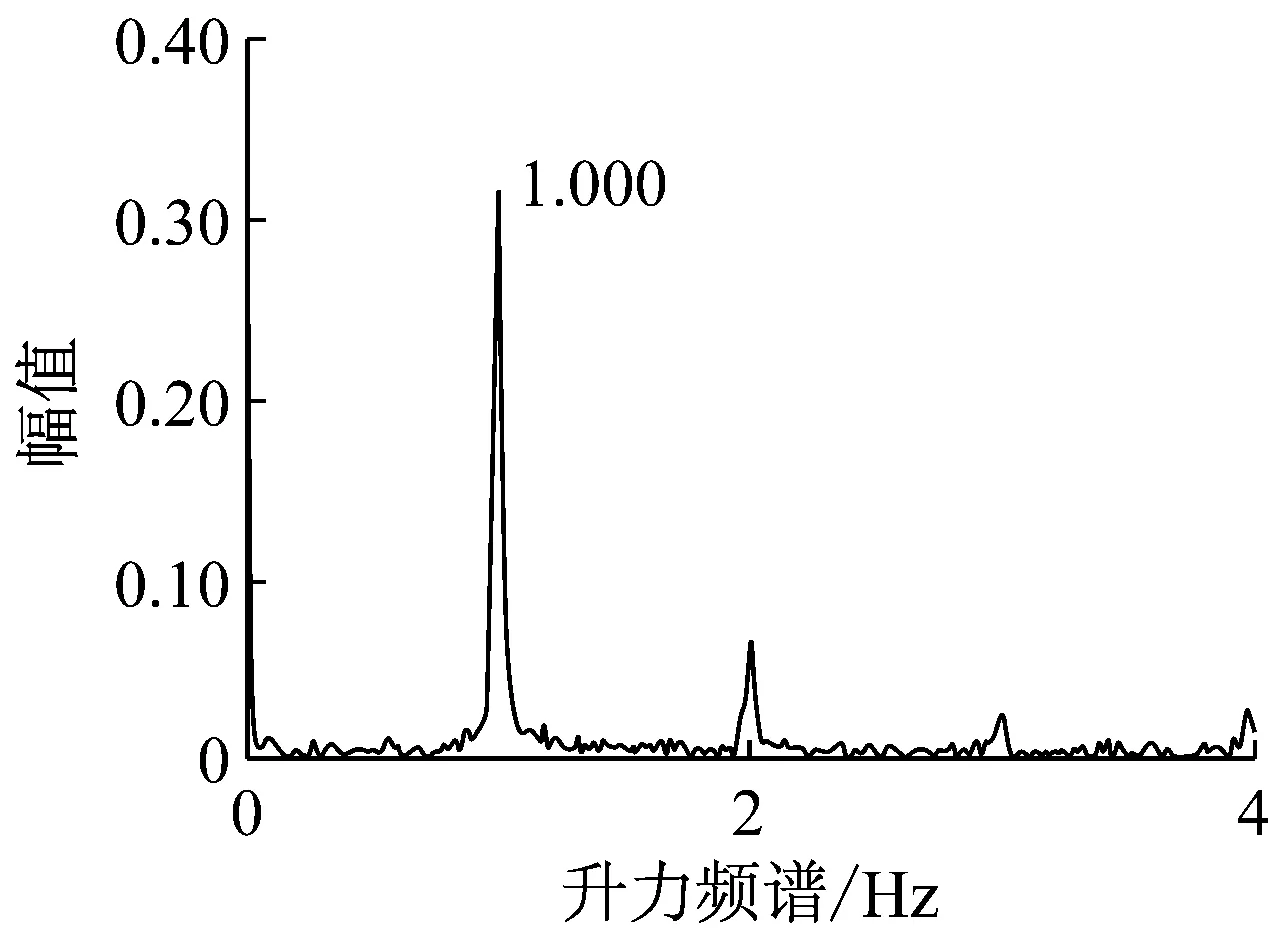
(c) 升力频谱分析(瞬态Cp、Cf)
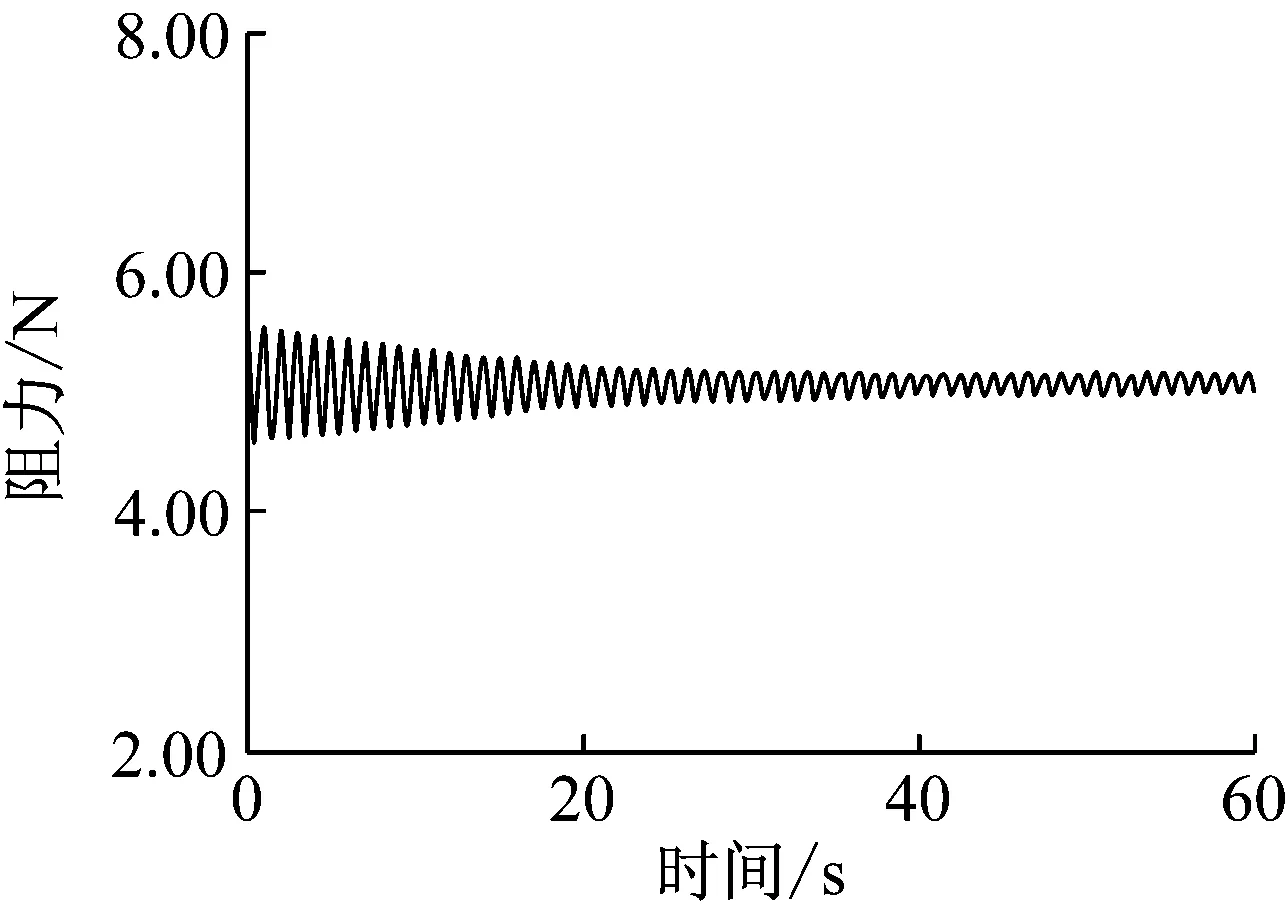
(a) 阻力时程曲线(固定Cp、Cf)
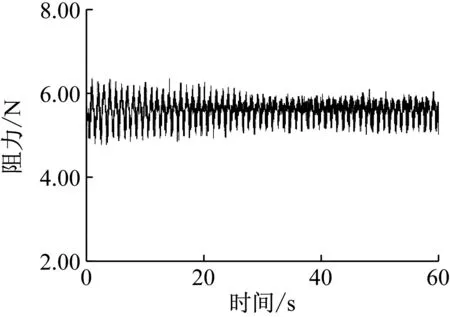
(b) 阻力时程曲线(瞬态Cp、Cf)

(c) 阻力频谱分析(瞬态Cp、Cf)
3.3 斜拉索振动响应
图14(a)显示了采用固定Cp、Cf的拉索振幅时程:其平衡位置在-0.25 m处,波动区间为-0.10 m~0.06 m,与实验结果[8]差别较大(平衡位置大约在0 m处,波动区间在-0.12 m~0.13 m左右)。如图14(b)所示,采用瞬态Cp、Cf的振动响应显示了与水膜形态、气动力变化一致的阶段性:t=0 s~20 s为剧烈变化阶段,在剧烈变化的气动力的作用下,拉索振幅迅速变大到-0.14 m~0.15 m;t=20 s以后为平稳变化阶段,周期性明显,平衡位置在0 m处,振幅区间为-0.13 m~0.15 m,与实验结果[8]符合良好,这表明,采用瞬态Cp、Cf更贴近风雨激振物理环境,使得计算结果更为准确,数值模拟更为合理。
如图14(c)所示:拉索振动响应振荡频率为fy≈1 Hz。综合结果得知,水线的振荡频率、气动力频率、拉索的振动响应频率,斜拉索的自振频率四者相近。另外根据陈文礼[9]的实验得知,U0=7.72 m/s位于风洞试验中发生风雨激振现象的显著风速范围内,结合水膜形态变化和气动力变化说明了风雨激振现象的气、液、固耦合机制:在激振风速范围内,包裹在拉索表面的水膜主要受气流和重力的作用形成上水线,并呈现周期振荡和滑落;水膜水线的周期性变化又导致了气动力的周期性变化;周期性变化的气动力和水线振荡作用在斜拉索上,又由于其变化频率与拉索自振频率相近,从而引发了拉索的受迫振动,发生共振;反过来,斜拉索的振动又影响水膜形态和气动力的变化,三者相互作用、相互影响。
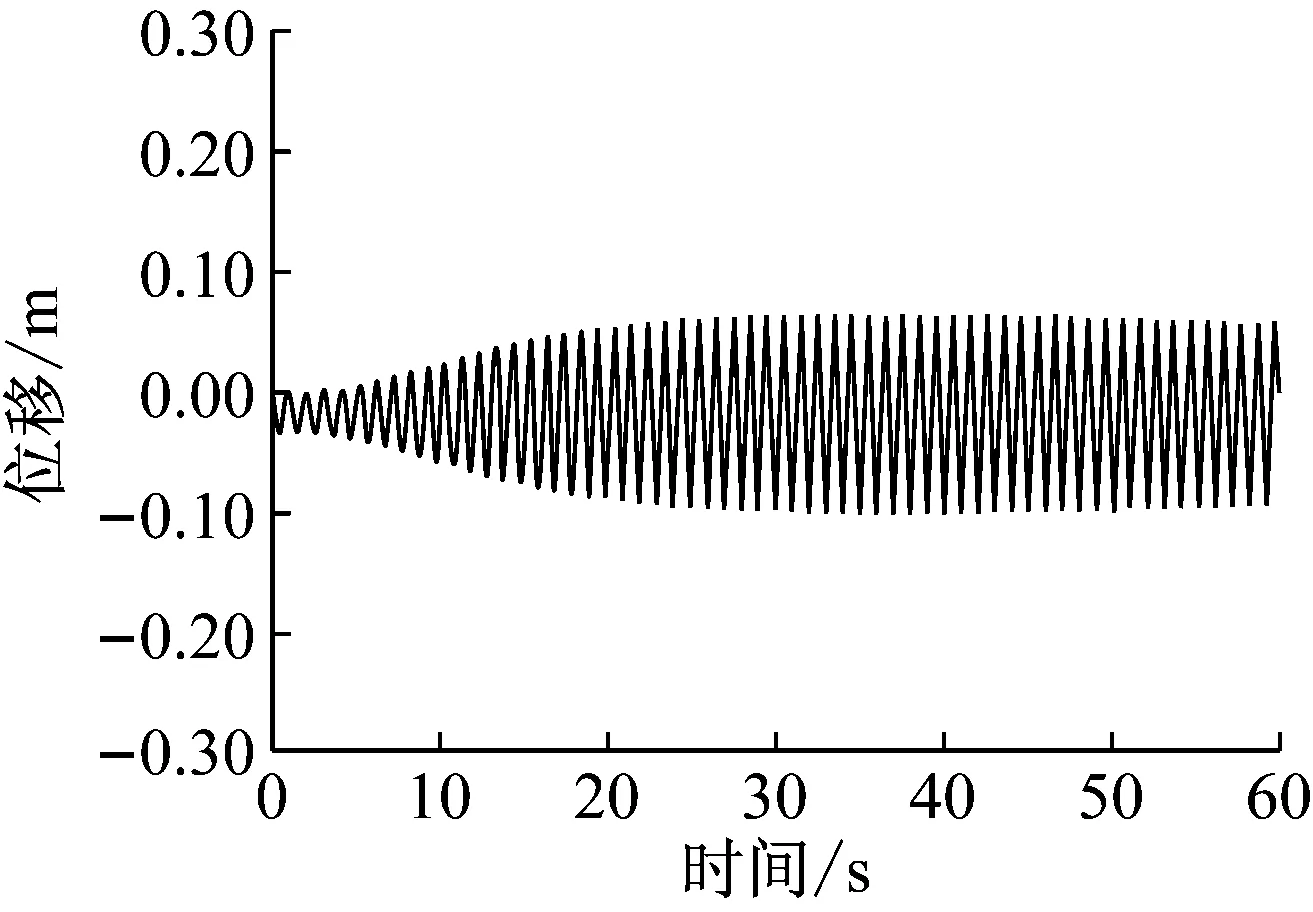
(a) 拉索振幅时程曲线(固定Cp、Cf)

(b) 拉索振幅时程曲线(瞬态Cp、Cf)
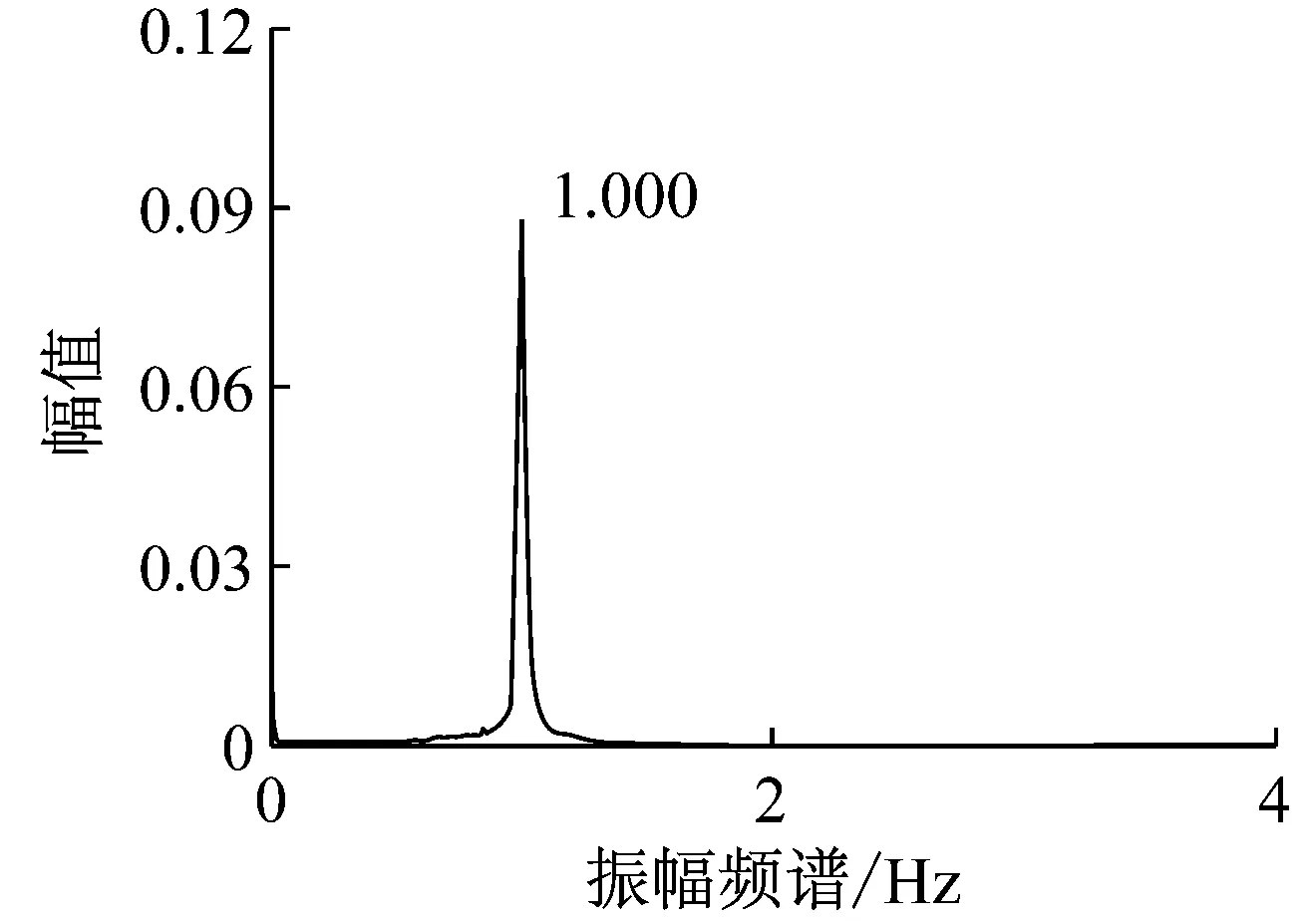
(c) 拉索振幅频谱分析(瞬态Cp、Cf)
4 结 论
本文将滑移理论与CFD技术相结合, 并基于S-A湍流模型,考虑随时间和位置变化的风压力和风摩擦因数,对斜拉索的风雨激振现象进行了数值模拟。通过考察水膜形态、气动力和拉索振动响应之间的关系,探究了风雨激振的产生机理,得到以下结论。
(1) 风速是上水线振荡和水膜形态变化的显著影响因素:风速在6 m/s~10 m/s范围内,随风速增大,水线形成时间变短,形成位置向背风侧移动;水线高度、宽度发生不同程度的增大和波动。
(2) 风雨激振状态下,上水线及水膜形态存在周期性的形成、滑落和振荡,并呈现了阶段性的发展过程:剧烈变化阶段、平稳变化阶段。
(3) 气动力的突变区域与上水线的振荡区域基本重合,上水线的振荡对风压力系数Cp和风摩擦因数Cf有重大影响,Cp和Cf受到影响的气动力又反作用于水膜形态,同时影响拉索振动。考虑Cp和Cf随时间和位置的变化和与水膜形态拉索振动的相互作用,对风雨激振的准确计算极其重要。
(4) 水线振荡、气动力变化、拉索振动相互作用,由于频率相近引发共振,是产生风雨激振现象重要因素之一。
[1] 顾明,李寿英,杜晓庆.斜拉桥拉索风雨激振理论模型和机理研究[J].空气动力学学报,2007,25(2)169-174.
GU Ming,LI Shouying, DU Xiaoqing. Testing study on wind pressure distributions of stayed cables with a fixed artificial rivulet[J]Acta Aerodynamica Sinica,2007,25(2)169-174.
[2] 刘庆宽, 张峰, 乔富贵. 轴向流对斜拉索气动稳定性影响的试验研究[J]. 石家庄铁道学院学报(自然科学版), 2008, 21(4): 16-19.
LIU Qingkuan, ZHANG Feng, QIAO Fugui. Effect of axial flow on rain-wind induced vibration of stay-cables[J].Journal of Shijiazhuang Railway Institute (NaturalScience), 2008, 21(4): 16-19.
[3] CHENG S, IRWIN P A, JAKOBSENL B, et al. Divergent motion of cables exposed to skewed wind[C] //Proc. of the 5th In.t Symposium on Cable Dynamics. Italy: Santa Margherita Ligure, 2003: 271-278
[4] BI J H,WANG J,SHAO Q,et al. 2D numerical analysis on evolution of water film and cable vibration response subject to wind and rain[J]. Journal of Wind Engineering and Industrial Aerodynamics,2013,121:49-59.
[5] LEMAITRE C,HÉMON P,DE LANGRE E. Thin water film around a cable subject to wind[J]. Journal of Wind Engineering and Industrial Aerodynamics,2007, 95(9/10/11):1259-1271.
[6] LEMAITRE C,DE LANGRE E,HÉMON P. Rainwater rivulets running on a stay cable subject to wind[J].European Journal of Mechanics-B/Fluids,2010,29(4):251-258.
[7] 王剑.斜拉索表面水膜形态及斜拉索气动力变化规律[J].天津大学学报(自然科学与工程技术版), 2014,47(4):1-12.
WANG Jian. Variation of water film morphology and aerodynamic force of stay cable[J]. Journal of Tianjin University(Science and Technology),2014,47(4):1-12.
[8] LI F C,CHEN W L,LI H, et al. An ultrasonic transmission thickness measurement system for study of water rivulets characteristics of stay cables suffering from wind-rain-induced vibration[J]. Sensors and Actuators A:Physical,2010,159(1):12-23.
[9] 陈文礼. 斜拉索风雨激振的试验研究与数值模拟[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2009.
[10] LI H,CHEN W L,XU F. A numerical and experimental hybrid approach for the investigation of aerodynamic forces on stay cables suffering from rain-wind induced vibration[J]. Journal of Fluids and Structures,2010,26(7/8):1195-1215.
[11] 中华人民共和国交通部.公路斜拉桥设计规范(试行):JTJ 027—96[S].北京:人民交通出版社,1996.
[12] 毕继红,王剑,逯鹏,等.不同风速下拉索表面水线的形成[J].天津大学学报(自然科学与工程技术版), 2014, 47(7):577-582.
BI Jihong, WANG Jian, LU Peng, et al. Formation of rivulets on cable surface under different wind speeds[J].Journal of Tianjin University(Science and Technology, 2014, 47(7):577-582.
Numerical simulation of rain-wind induced vibration of stay cables and its mechanism study
BI Jihong1, 2, WU Ji1, GUAN Jian1, WANG Jian3,4
(1. School of Civil Engineering,Tianjin University,Tianjin 300072,China;2. Key Laboratory of Coast Civil Structure Safety,Ministry of Education,Tianjin University,Tianjin 300072,China:3. School of Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China;4. Key laboratory of Soft Soil Characteristic and Engineering Environment of Tianjin,Tianjin 300384,China)
Using the lubrication theory combined with the computational fluid dynamics(CFD) method, considering wind pressure coefficient and wind friction one changes with variation of position and time, introducing Spalart-Allmaras(S-A) turbulence flow model and adopting the finite element method, the numerical simulation for rain-wind induced vibration (RWIV) phenomena of stay cables was realized. To verify the reasonableness and correctness of this method,the formation and morphology of rivulets at different wind speeds were inspected,and they were compared with the existing test results. Through investigating the relations among water film morphology, lift variation and vibration responses of stay cables, vibration coupling laws between rivulets and stay cables were obtained, the mechanism of RWIV were explored. Similar to test results, the simulation ones showed that the resonance among upper rivulet, lift and stay cables is one of the main factors to cause RWIV.
rain-wind induced vibration;rivulet;lift;vibration of cable
国家自然科学基金(51408399)
2015-12-30 修改稿收到日期:2016-03-25
毕继红 女,博士,教授,1965年生
U443.38
A
10.13465/j.cnki.jvs.2017.11.017
