南海张力腿平台气隙计算方法*

王火平 刘义勇 冒家友 冯丽梅 李龙祥

(中海石油(中国)有限公司深圳分公司深水工程建设中心 广东深圳 518067)

南海张力腿平台气隙计算方法*

王火平 刘义勇 冒家友 冯丽梅 李龙祥

(中海石油(中国)有限公司深圳分公司深水工程建设中心 广东深圳 518067)

王火平,刘义勇,冒家友，等.南海张力腿平台气隙计算方法[J].中国海上油气，2017,29(2)：142-146.WANG Huoping,LIU Yiyong,MAO Jiayou,et al.Calculating method of the airgap for TLPs in South China Sea[J].China Offshore Oil and Gas,2017,29(2):142-146.

气隙是张力腿平台性能的重要指标之一。通过对张力腿平台气隙设计要求及影响因素进行分析，给出了张力腿平台气隙预报模型。以流花16-2油田为例，结合张力腿平台前端工程设计研究项目，采用气隙简化估算公式、数值模拟和模型试验相结合的方法进行了气隙计算。计算结果表明，在前期工程设计或初步设计时，可采用本文给出的简化估算公式快速计算气隙，对于最终设计气隙，建议以数值模拟和模型试验相结合的方法来确定。本文提出的张力腿平台气隙设计方法可为南海今后类似张力腿平台设计提供借鉴。

张力腿平台；气隙；预报模型；气隙简化估算；数值模拟；模型试验

张力腿平台(TLP)作为一种典型的深水浮式平台，具有运动性能优良、可采用干式采油树开发、适用水深范围广(300～1 500 m)等优点，在国外深海油气开发中得到了广泛应用。目前国外已建成TLP平台27座，其中17座位于墨西哥湾。2015年中国海洋石油总公司首次以南海流花16-2油田为应用目标，完成了TLP前端工程设计和研究工作，以探求适应南海深水油气开发特点的更多深水浮式平台技术。

流花16-2油田地处台风频发的南海北部区域，如何确保TLP平台在恶劣环境下的安全可靠性是工程设计中面临的严峻挑战。在TLP诸多安全性能指标中，气隙作为衡量平台主甲板是否远离波浪拍击区域的一个重要指标，是TLP设计的重点。目前对于半潜式平台的气隙预报国内已经有所研究[1-2]，但是对于TLP这种类型的浮体，气隙的研究还尚在进行且无实际工程设计应用。国外对于浮体结构的气隙研究主要集中在数值模拟[3-7]和模型试验[8-10]等方面，对于在设计早期阶段如何快速有效地预报TLP平台气隙，在工程详细设计阶段如何合理有效地利用模型试验结果准确给出平台气隙，以及在TLP设计中可以直接应用的具体方法很少涉及。本文结合南海流花16-2油田TLP前端工程设计研究项目，通过对TLP气隙设计要求进行分析，给出了TLP气隙响应的预报模型，并采用简化公式、数值模拟和模型试验相结合的方法进行了气隙计算。

1 TLP平台气隙设计要求及预报模型

1.1 气隙设计要求

TLP由上部组块和下浮体两部分组成，其中上部组块由上部生产设施模块、生活楼和钻井模块等组成，下浮体由主船体(包括立柱和浮箱)、立管系统、张力腿系统、桩基础系统等组成。根据规范[11-12]TLP气隙定义为在各种计算工况下TLP下层甲板大梁底部至最大波峰面之间的垂直距离(图1)，平台下层甲板大梁底部至平均海平面的垂直距离则定义为初始气隙(或最小甲板间隙)。为确保TLP在恶劣环境条件下安全可靠，平台应具有足够的甲板高度。根据API RP 2T规范[11]推荐，百年一遇台风重现期极端工况下平台气隙建议不小于1.5 m，千年一遇台风重现期生存工况下建议不小于0，但如果出现轻微程度的负气隙，需要进一步分析证明在千年一遇最大波峰的冲击下平台不会出现整体失效。

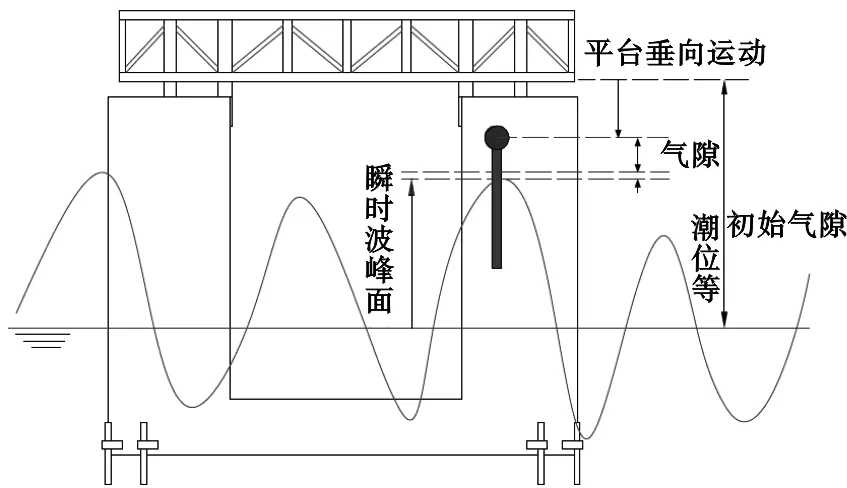
图1 TLP气隙定义示意图Fig .1 Definition of TLP airgap

此外，气隙满足规范要求后也不能有过大的余量，否则会抬高平台的重心位置，增加风载荷和风矩，进而影响TLP的总体性能、张力腿的最小张力和最大张力，使得浮体排水量增大和张力腿尺度增大，平台的投资也会相应增加。因此，准确预报平台气隙十分重要，不仅有利于确保平台安全可靠，还可以适当降低平台造价。TLP气隙设计时应考虑以下因素。

1) 平台运动响应引起的下沉量。不同于固定平台，TLP在恶劣环境下会发生较大偏移而产生下沉或垂向运动，从而引起甲板相对于水平面的高程减小，其下沉量随着平台偏移量增加而非线性增加，环境条件越恶劣，甲板高程减少会越多。

2) 最大波峰面高度。根据波浪理论，波浪经过漂浮结构时，最大波峰面高度由非线性波的波峰面高度和爬坡效应引起非线性的自由表面升高叠加而成。在极端海况下，入射波表现出较强的非线性特征，极值波浪的波峰和波谷表现出的不对称性非常明显。由于TLP平台立柱尺度较大，入射波经过立柱时会产生辐射绕射作用，从而引起自由表面升高。这种自由表面升高称为爬坡效应，表现为波浪沿平台立柱向上爬升，波浪的爬升过程从理论上可解释为当入射波浪冲击浮体时，水波的动能转化为势能同时波高发生放大的过程。

3) 其他因素。在确定平台气隙时，还须考虑风暴增水和潮汐(合为高潮水位)以及平台寿命期内可能发生的地质沉陷和海平面上升引起的水位增加。

1.2 平台气隙预报模型

如图1所示，假定初始气隙为ZDC，平台底部垂向运动为ZDK，瞬时波峰面高度为ZF,风暴增水和潮汐为ZTD，平台寿命期内可能发生的海底沉陷和海平面上升分别为ZSUB和ZSR,某工况下的平台甲板底部某点的气隙Z可通过式(1)求得(波面高是瞬时概念，应表示为ZF(t),相应的平台下沉和潮汐都是瞬时概念)

(1)

考虑将平台垂向运动和波峰面高度合并为一项，即ZDK+ZF=ZRC，ZRC称为相对波峰面高度，则可将式(1)简化为

(2)

从式(2)可知，求得平台最小气隙(设计气隙)的关键是要求出平台的最大相对波峰面高度，包括平台的瞬时垂向运动和波峰面高度，则式(2)可变为

(3)

最大相对波峰面高度是波峰面相对于平台底部某点位置的距离，可通过波峰面高度减去某点的垂向运动，最终的气隙可通过初始气隙减去相对的波峰面高度求得。平台的垂向运动和波峰面高度是2个未知的非线性分量，可通过水动力分析求得。业界现在采用的绕射和辐射分析软件尚不能准确计算波浪的非线性部分，因此在计算相对波峰面高度时须对波浪的非线性项进行修正(即叠加波浪的高阶分量)，即

(4)

式(4)中：ZRCmax(1storder)为一阶波产生经分析数值软件拟合后的最大相对波峰面高度，ηmaxdesign为根据实际海况在不同重现期的最大波峰面设计值，ηmax(numerical)为在分析软件模拟得到的一阶波浪的最大波峰面，两者差值为Δη。

2 计算实例

TLP气隙计算涉及到非线性因素，是一个非常复杂的问题。因此计算TLP气隙时一般采用时域数值模拟方法，最后结合模型试验结果对平台气隙进行适当修正。但是在工程设计初期或进行总体尺度初始规划时，采用必要的简化方法计算气隙能节省大量的时间和工程计算。本文以流花16-2油田TLP前期工程设计方案为例介绍TLP气隙的计算方法，该平台工作水深约为400 m，采用经典的四立柱传统型TLP，设计寿命为20 a，设计排水量约5.0×104t，上部组块操作质量约1.5×104t，船体质量约1.57×104t，布置有8根张力腿和12根顶张式立管，张力腿在泥面位置与桩基础直接相连，平台主尺度及设计环境条件数据分别见表1和表2。结合流花16-2油田及油藏特点，在本研究中不考虑TLP平台寿命期内可能发生的海底沉陷和海平面上升。

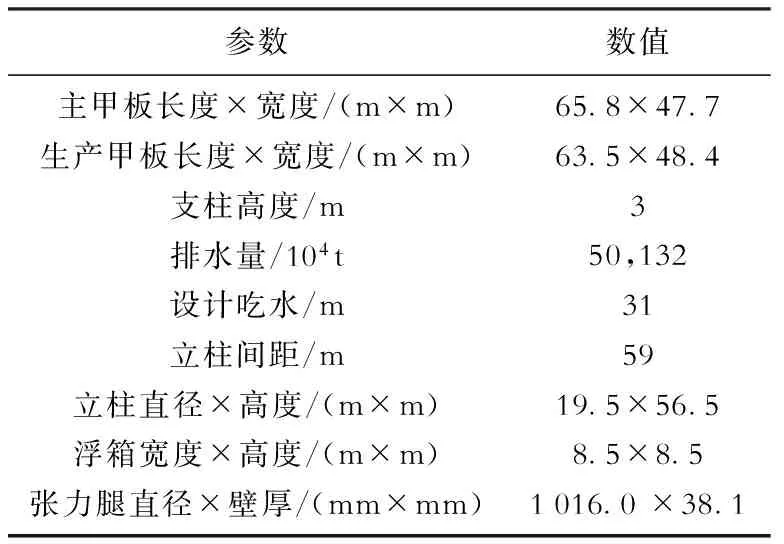
表1 流花16-2油田TLP平台主尺度Table 1 Principal dimensions of the TLP in LH 16-2 oilfield

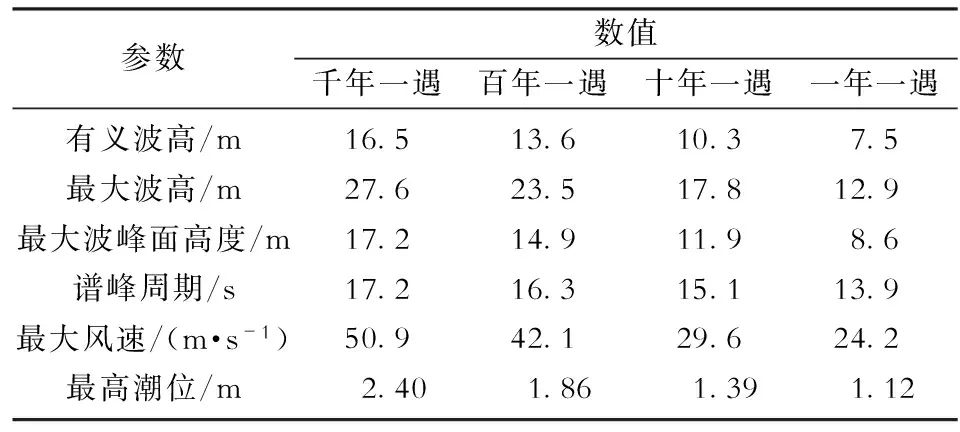
表2 流花16-2油田TLP平台设计环境条件数据Table 2 Environmental condition design data for the TLP in LH 16-2 oilfield

2.1 气隙简化估算

在前期工程设计阶段，需要确定平台总体尺度，特别是平台的高程，借鉴式(1)给出简化计算方法可以快速有效地给出最小气隙的估值:

(5)

式(1)中的瞬时波峰面高度ZF被αHs代替，该项包含绕辐射作用下的最大波峰面高度Hs以及实际海况下最大波峰面高度的修正参数α。不同的海域α会有所不同，但是一般在台风主导的区域α值建议取1.4～1.5，建议在墨西哥湾取上限值1.5,在中国南海取下限值1.4。与之相对应的公式(5)中的ZDK对应的是平均垂直运动，传统四立柱TLP 225°浪支配的工况一般是最小气隙的关键工况。以流花16-2油田TLP前期设计方案为例，利用本文简化估计公式，在千年一遇台风最大浪工况下，取ZDC=29 m,ZDK=2.42 m,α=1.45,Hs=16.5 m,ZTD=2.4 m,ZSUB=0,ZSR=0，最小气隙为0.255 m。

2.2 气隙数值计算

气隙数值计算主要有2个关键因素，一是找到平台气隙设计的最不利点，二是通过时域分析方法求得该点的相对最大波峰面高度。TLP气隙不利点一般都是在顺浪立柱的内侧点，图2给出了流花16-2油田TLP数值模拟计算选取的气隙研究点示意图。

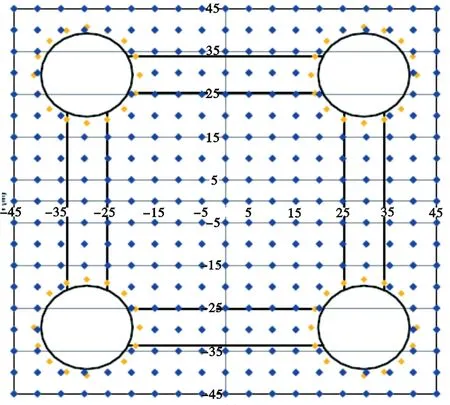
图2 流花16-2油田TLP平台最不利气隙点筛选Fig .2 Points of interest for airgap analysis in LH 16-2 oilfield

筛选出气隙的最不利位置后，通过时域数值分析求得TLP平台6个自由度的运动时程，之后通过韦布尔拟合方法求得可能的数值分析的最大波峰面高度。图3中显示了波面高度的运动时程，波面高度是从数值模拟软件中得到。波高的时域曲线一般是通过多个规则波的波浪分量叠加得到的，这个波高指的是平台研究对象正下方那一点对应的波高。

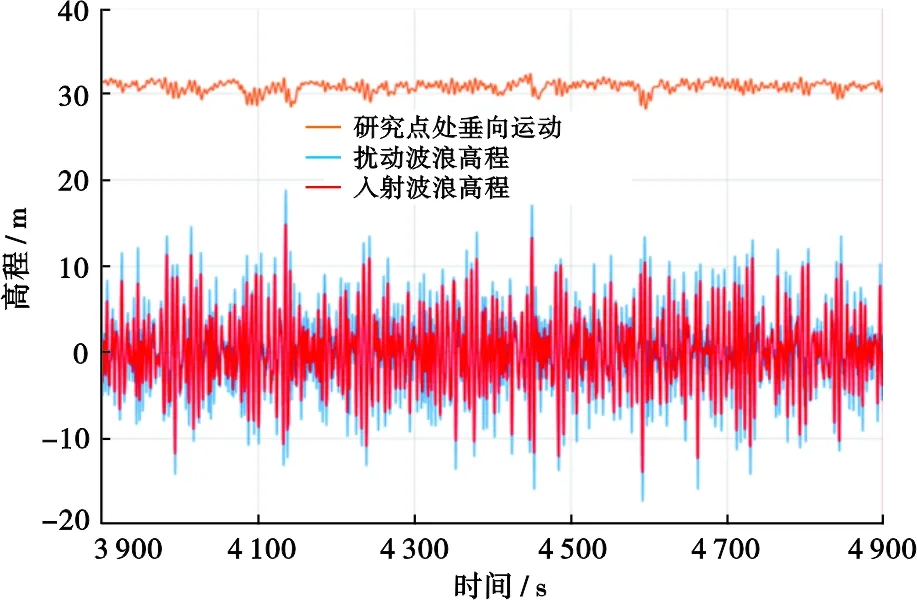
图3 数值分析方法得到的流花16-2油田TLP平台 最不利点的相对波峰面高度Fig .3 Maximum relative wave crest derived from numerical analyses of TLP platform in LH 16-2 oilfield 在工程详细设计阶段， TLP平台最小气隙一般都采用时域数值模拟和模型试验数据相互结合的方法确定。TLP气隙计算数值模拟以及试验校核方法的基本步骤如下。

1) 定义好各个感兴趣的点后，通过绕辐射软件得到各个点波面高度的运动响应RAO，包括入射、绕射和辐射的线性部分，并筛选出最不利的气隙位置。

2) 通过时域运动分析软件进行平台的运动分析求得指定点的平台运动时程(波峰面高度和平台垂向运动)。之后连同从步骤1)中获得的RAO进行处理，计算指定点的相对瞬时波峰面高度(包括入射波、绕射和辐射的线性部分及平台垂向运动)。

3) 通过韦布尔拟合的统计分析，得到关键点最大相对波峰面高度和STDV标准差(包含了TLP运动、一阶入射波、绕射和辐射)。

4) 在步骤3)中获得的只有一阶入射波， 其最大波峰和实际海况取得的最大波峰相比缺少了非线性部分，因此在时域运动软件对一阶入射波进行统计分析，利用实际海况给予的最大波峰对在步骤3)中获得的最大相对波峰面进行修正，然后进行下一步的模型试验修正。

5) 模型试验修正，其方法为

(6)

(7)

(8)

式(6)～(8)中：Fcorr为模型试验结果的标准差修正系数；Fextreme为模型试验的极值修正系数；ZRCSTDV为从数值模拟中获得的相对波峰的标准差;RCSTDVmodel为从模型试验结果得到的统计值模型标准差；RCSTDVnumerical为从数值分析得到的统计值数值标准差；RCmaxmodel为从模型试验结果得到的统计值模型极值。

平台设计气隙经模型试验结果修正后的公式为

(9)

6) 潮位等数据修正，得到最终设计气隙数据。南海潮差较大，千年一遇最高潮位达2.4 m，本研究把潮位直接扣除可能略有保守，建议在TLP详细设计阶段对其敏感性作进一步研究。

2.3 气隙计算

在流花16-2油田TLP平台气隙实际计算时，分别考虑了百年一遇和千年一遇环境条件下现行规范要求的各种分析工况，根据总体性能分析结果，225°海浪支配的工况为气隙计算的控制工况。为取得TLP平台模型试验数据，在国内某水池试验进行了1∶50比例水动力模型试验(图4)，求得百年一遇和千年一遇225°海浪支配工况的最小气隙。

图4 TLP平台模型试验Fig .4 TLP model testing

百年一遇和千年一遇台风225°海浪工况下最小气隙计算过程见表3，从表3可知，百年一遇和千年一遇时最小气隙分别为2.68 m和-0.82 m，百年一遇的工况满足API RP 2T(2010)规范要求；千年一遇时甲板大梁底部会遭受波浪砰击(甲板底部大梁高度为1.5 m)，在详细设计时须考虑对甲板大梁进行局部加强，以确保平台的安全可靠性。

根据本文提供的简化公式计算，千年一遇时得出的最小气隙0.255 m，与经过时域数值模拟和模型试验修正的最终结果相差约1 m。考虑到最小气隙计算的复杂性，该误差在工程设计初期或进行总体尺度初始规划阶段应该属于可接受范围内。

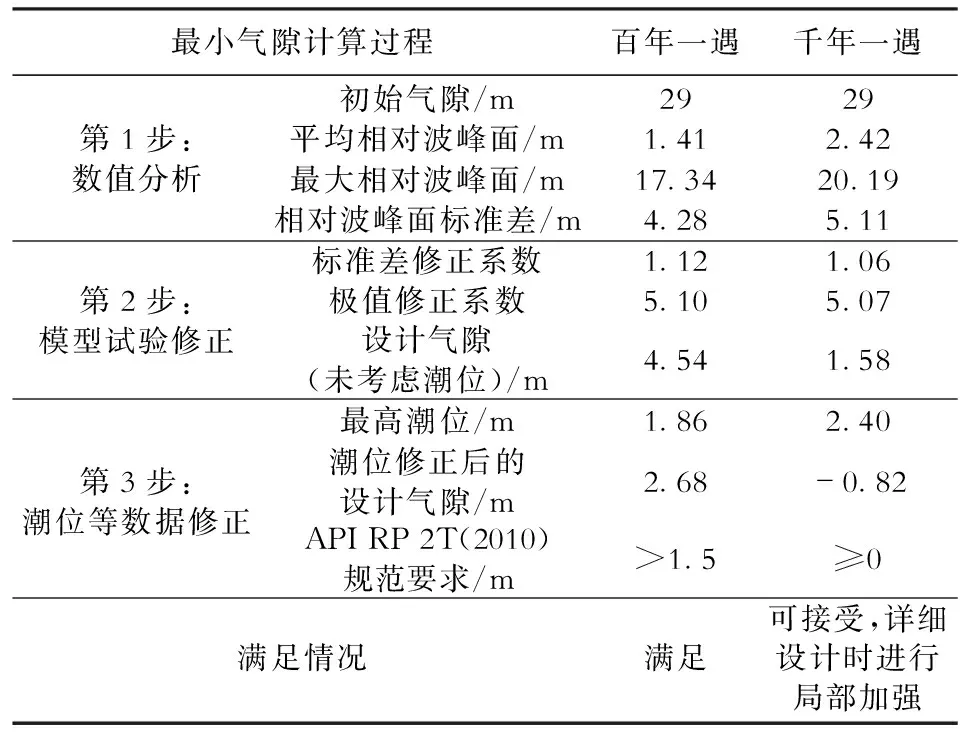
表3 百年一遇和千年一遇台风225°海浪工况下 最小气隙计算过程Table 3 The model test correction factors and the minimum airgap for 100-year and 1000-year return period typhoon under 225° wave dominant condition

3 结论

在前期工程设计或初步设计时，确定TLP平台主尺度时可采用本文给出的简化公式快速计算气隙。由于TLP气隙预报涉及很多复杂的非线性分析，因此对于最终设计气隙，建议以数值模拟和模型试验相结合的方法来确定。

[1] 陶晶晶.半潜式平台气隙响应的计算研究[D].大连：大连理工大学，2008. TAO Jingjing.Computational analysis of the airgap responses for semi-submersible platforms[D].Dalian:Dalian University of Technology,2008.

[2] 曾志.半潜式平台气隙响应的预报[D].上海：上海交通大学,2009. ZENG Zhi.Analytical prediction of the airgap responses for semi-submersible platforms[D].Shanghai:Shanghai Jiao Tong University,2008.

[3] MANCE L,SWEETMAN B,STEVEN R.Analytical predictions of the air gap response of floating structures[J].Journal of Offshore Mechanics and Arctic Engineering,2001,123(3):112-117.

[4] SWEETMAN B,WINTERSTEIN S R,MELING T S.Airgap prediction from second-order diffraction and Stokes theory[J].International Journal of Offshore and Polar Engineering,2002,12(3):184-188.

[5] SWEETMAN B,WINTERSTEIN S R.Non-Gaussian air gap response models for floating structures[J].Journal of Engineering Mechanics,2003,129(3):302-309.

[6] WIINTERSTEIN S R,SWEETMAN B.Air gap response of floating structures:Statistical predictions versus observed behavior[J].Journal of Offshore Mechanics and Arctic Engineering,2001,123(3):118-123.

[7] TEINGEN P,NIEDZWECKI J M,WINTERSTEIN S R.Wave interaction effects for non-compliant TLP[C].Proceedings of the International Offshore and Polar Engineering Conference,2001:453-461.

[8] OLEG G,ARYVID N,STANSBERG C T.Airgap statistics for a tension leg platform[C].ASME 31st International Conference on Ocean,Offshore and Arctic Engineering,2012:25-31.

[9] MERCIER R S,SCHOTTLL C T,HOWELL E B,et al.Mars TLP use of scale model testing in the global design[R].OTC 8354,1997.

[10] FORRISTALL G Z.Maximum crest heights under a model TLP deck[R].OMAE 49837,2011.

[11] API.API RP 2T.Planning,designing and constructing tension leg platforms[S].2010.

[12] ABS.Rules for building and classing floating production installations[S].2015. 收稿日期：2016-07-13 改回日期：2016-10-21

(编辑：叶秋敏)

Calculating method of the airgap for TLPs in South China Sea

WANG Huoping LIU Yiyong MAO Jiayou FENG Limei LI Longxiang

(DeepwaterEngineeringandConstructionCenter,ShenzhenBranchofCNOOCCo.Ltd.,Shenzhen,Guangdong518067,China)

Airgap is one of the important parameters for tension leg platforms (TLPs). Based on the investigation of the TLP airgap design criteria and the influencing factors, an airgap prediction model was derived. Combining the front engineering research project, this paper presents a case study carried out for Liuhua 16-2 TLP FEED project in South China Sea, and the airgap was calculated by combining the simplified estimation formula, the numerical analysis, and model tests. The results demonstrate that the simplified method for airgap calculation presented here can be utilized during early or preliminary stage of TLP design; however, for the final design, the model test is highly recommended in conjunction with the numerical calculations. The airgap design methodology presented in this paper can be applied in future TLP projects in South China Sea.

tension leg platform; airgap; prediction mode; airgap simplification estimation; numerical simulation; model test

*国家工信部高技术船舶科研项目“500米水深油田生产装备TLP自主研发”部分研究成果。

王火平，男，工程师，2004年毕业于广东海洋大学，获船舶与海洋工程学士学位，现主要从事深水油气田开发工程建设管理工作。地址：广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座37楼(邮编：518067)。E-mail:wanghp5@cnooc.com.cn

1673-1506(2017)02-0142-05

10.11935/j.issn.1673-1506.2017.02.020

TE952

A