基于改进熵值法的装备维修保障能力灰色评估

吕瑞强，胡 涛，杨 阳

（空军勤务学院，江苏 徐州 221000）

基于改进熵值法的装备维修保障能力灰色评估

吕瑞强，胡 涛，杨 阳

（空军勤务学院，江苏 徐州 221000）

装备维修保障能力评估的准确度直接影响到装备的保障效能。在评估中，指标权重的确定尤为重要。针对熵值法赋权中单一指标权重过大，影响评估结果的问题，借鉴AHP赋权法，构建基于指标信息熵的判断矩阵来求解权重，克服了熵值法单一指标权重可能过大的问题。最后采用灰色系统理论对装备的维修保障能力进行了评估，通过分析评估结果，验证了该方法的正确性。

改进熵值法，维修保障，灰色评估

0 引言

在装备维修保障能力的评估中，指标权重的确定尤为重要［1］。科学地确定指标权重是准确评估的基础。确定指标权重的方法有主观赋权法和客观赋权法，主观赋权法是依据评估者个人主观偏好对评估指标赋值计算权重，但由于个人的偏好不同，存在确定的指标权重有很大的主观不确定性，如AHP法。客观赋权法依据指标数据信息来计算权重，如熵值法。该方法赋权具有较强的客观性，减轻了决策者的负担，并具有较强的数学理论依据，但在使用中会出现当某一指标的指标值离散程度较大时，该指标的权重过大，导致单一指标影响最终的评估结果［2-4］。针对主观赋权法和客观赋权法在实际中存在的问题，本文对传统的熵值法进行了改进，结合AHP赋权法的思想，通过构造基于指标信息熵的判断矩阵来求解权重，克服了熵值法单一指标权重可能过大影响评估结果的问题。最后根据确定的权重，运用灰色评估法对装备维修保障能力进行评估，验证了改进熵值法的合理性，对提高装备维修保障能力的评估准确性具有一定的使用价值。

1 改进熵值法原理

1.1 传统熵值法

熵值法在确定指标权重时，由于各指标所包含的信息量不同，导致它们对评估系统的影响程度不同。当某一指标在各评估对象中的差异较大时，说明其包含的信息量多、对评估系统的影响大，该指标权重应该较大；如果某项指标的指标值全部相等，则该指标在综合评价中不起作用。

①对各指标数据进行规范化，消除各评价指标的量纲影响，将指标数据归一化处理。对于越大越优型指标的处理公式为：

对于越小越优型指标的处理公式为：

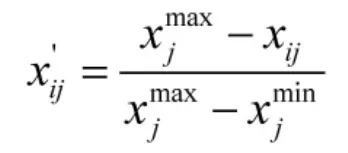
②计算第j项指标下第i个评估对象指标值的比重pij：

③计算第j项指标的熵值ej：

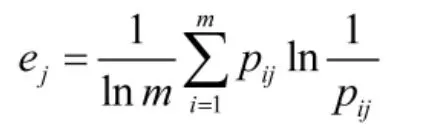
④计算第j项指标的差异性系数gj：

1.2 改进型熵值法

改进型熵值法针对传统熵值法存在的问题，借鉴AHP赋权法的思想，构造了基于指标信息熵的判断矩阵，采用1～9标度对指标差异性系数的两两比较结果进行辨识，得到了标度映射值，并在此基础上构造了改进型熵值法的判断矩阵，计算出了指标的权重值。其方法步骤为：

①依据熵值法赋权步骤，求出各指标的差异性系数。

②求最大的差异性系数比D：

③求1～9标度的映射比率：

式中，a为调整系数，表示在改进熵值法中使用的最大标度值。若D≤9，则a取最接近D的整数，否则取a=9。式中开a-1次方是将D平均分配在1～9标度的映射值上，用D除以a是使改进熵值法的l～9标度的映射值与AHP赋权法中的1～9标度有更一致的结构。

④计算1～9标度的映射值。改进熵值法的计算1～9标度映射值是在AHP赋权法中的1～9标度的基础上乘以R的原标度值减一次方得出的。l～9标度和其映射值间的对应关系如表l所示。

表1 1～9标度、映射值对照表

⑥计算指标的权重值。构造出基于信息熵的判断矩阵后，求指标权重的方法和AHP赋权法相同。

2 灰色评估法

灰色系统理论的研究对象是“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统。灰色评估模型在兼顾贫信息和样本区间的模糊性的基础上，将灰色系统尽可能地白化、量化、模型化，以期用较少的数据实现对样本评估。其主要步骤是：计算评估指标值矩阵、确定评估灰类、建立三角白化权函数，计算灰色评估系数、评估权向量和权矩阵，最后进行综合评估［5-6］。由于篇幅所限，在此不作详细介绍。

3 实例分析

本文通过部队调研和大量的数据分析，结合专家经验，基于改进熵值法确定指标权重，运用灰色评估方法来分析装备维修保障能力。

3.1 装备维修保障能力评估指标的建立

考虑装备维修保障系统工作的多方面因素，并结合维修保障能力的定义，在参考大量相关文献的基础上，将影响装备维修保障能力的主要因素归纳为装备品质、人力资源、维修体制、手段设施、备件保障和维修管理6个方面［7］。通过基层部队的实地调研，收集整理大量的数据资料，经过征求专家意见，取舍合并，建立了装备维修保障能力评估指标体系［8-9］，如图1。

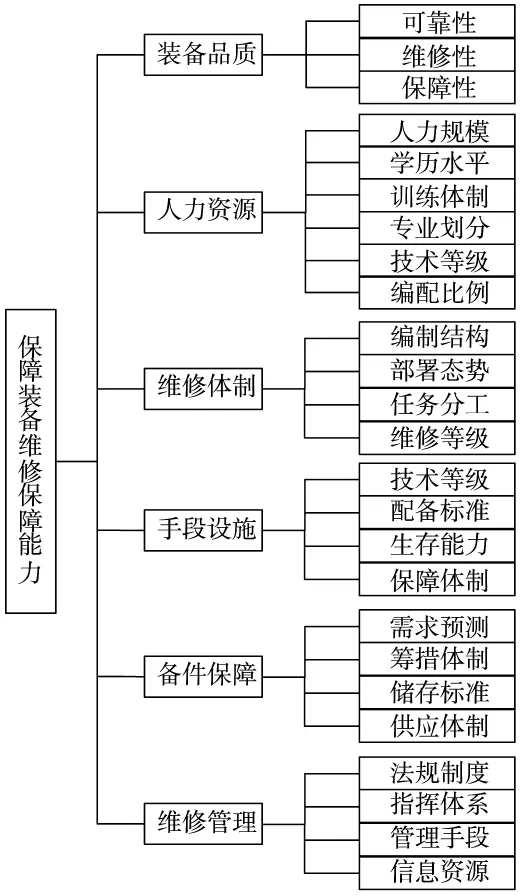
图1 装备维修保障能力评估指标体系

表2 各指标差异性系数

表3 改进熵值法1～9标度的映射值

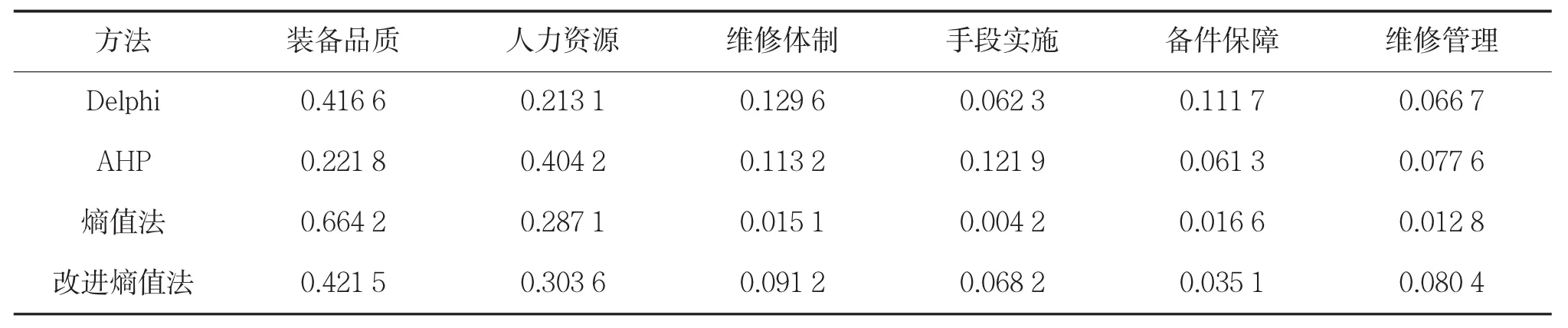
表4 不同赋权法得到的指标权重对比表

3.2 确定权重

根据建立的指标，运用改进熵值法求出了指标的差异性系数、1～9标度的映射值和权重值，并列出了用Delphi、AHP和熵值法计算的指标权重值，进行对比分析［10］。具体见表2～表4。

3.3 灰色评估

依据灰色评估理论原理，确定“优”、“良”、“中”、“差”4个评估灰度，并将各评价灰类等级按“灰水平”赋值，评价等级向量C=（9，7，5，2），分别对应“优”、“良”、“中”、“差”。最后计算出综合评价结果，如表5。

表5 指标维修保障能力评估值对比表

3.4 结果分析

从表4可以看出，Delphi和AHP赋权法由于主观偏好的因素，得到的权重值排序存在不同，各指标的权重值相差较大。而熵值法和改进的熵值法对指标赋权的权重排序不变，但在熵值法中，装备品质和人力资源占的比重分别达到66.42%和28.71%，占据了绝大部分权重值，而手段实施只占了0.42%，这与实际是不相符合的，使得手段实施指标在评估过程中几乎不起作用。改进熵值法中，装备品质权重从66.42%降到42.15%，手段实施权重从0.42%提高到6.82%，在保持指标权重排序基本不变的情况下，权重的最大值与最小值之比由158.143减少到6.18，这与Delphi和AHP法赋权得到的权重比相当，并且各指标权重值分布更加合理。

从表5可以看出，不同赋权法最后得到的装备维修保障能力评估结果都为“良”类，但改进熵值法与由熵值法得到的评估值有一定的差距，与Delphi和AHP法最后的评估值更为接近，这是由于在赋权时，熵值法赋权时个别指标的权重值过大或过小，使得权重比过大，影响了评估结果。改进熵值法确定指标权重的方法是合理有效的，提高了装备维修保障能力评估的准确性。

4 结论

对装备维修保障能力进行评估是检验部队保障能力的最直接方法，是提高部队整体作战能力的最有效的时间活动。在评估过程中，指标权重的确定尤为重要，决定着评估结果的正确与否。本文对传统熵值法进行了改进，运用灰色评估方法对装备维修保障能力进行评估，通过与Delphi、AHP和熵值法得到的结果进行比较分析，取得了较好结果，表明改进熵值法赋权更加合理，得到的评估结果更加可信。并且该方法还可以推广到其他的评估中。

［1］舒正平，周盛华.装备维修保障效能评估指标权重组合赋权法的研究［J］.兵工自动化，2010，29（12）：9-13.

［2］彭涛，阮拥军，尹波等.装备维修保障方案评估研究［J］.计算机与数字工程，2013，341（7）：1116-1118.

［3］曹会智，李帅，周启翔，等.基于SPA和改进熵值法的车辆装备维修机构工作绩效评价研究［J］.军事交通学院学报，2011，13（1）：25-28.

［4］黄国庆，王明绪，王国良.效能评估中的改进熵值法赋权研究［J］.计算机工程与应用，2011，30（6）：245-248.

［5］汪应洛.系统工程［M］.北京：机械工业出版社，2008：120-125.

［6］刘思峰，谢乃明.灰色系统理论及其应用［M］.北京：科学出版社，2013.

［7］吕瑞强，朱焕勤.多机种保障装备保障模型研究［M］.北京：蓝天出版社，2012：166-189.

［8］姚志龙，董辉平，周华龙，等.装甲装备基层级维修保障能力评估指标体系［J］.四川兵工学报，2009，20（5）：107-109.

［9］常春贺，曹鹏举，王晗中，等.雷达维修保障系统效能评估研究［J］.现代雷达，2011，33（1）：12-17.

［10］张飞马，刘超.地空导弹装备战场抢修组合赋权效能评估［J］.四川兵工学报，2014，25（9）：62-64.

Grey Evaluation of Equipment Maintenance Support Capability Based on Improved Entropy Method

LYU Rui-qiang，HU Tao，YANG Yang
（Air Force Logistics College，Xuzhou 221000，China）

The accuracy of equipment maintenance support capability assessment directly affects the efficiency of equipment support.In the evaluation，the determination of index weights is particularly important.According to the weight of a single index method of entropy weighting in large impact assessment results of the problem.Using AHP weighting method，the judgment matrix is constructed based on the index information entropy to solving weights and overcome the entropy method for single index weight may be too large.Finally，the maintenance support capability of the equipment is evaluated by the grey system theory，and the correctness of the method is verified by analyzing and evaluating the results.

improved entropy method，maintenance support，grey evaluation

E072

A

1002-0640（2017）05-108-04

2016-02-16

2016-04-17

吕瑞强（1964- ），男，江苏徐州人，博士，教授。研究方向：航空四站保障技术与信息化。