状态维修下通指装备可用度评估

刘欢庆，罗长远，庞松超

（解放军信息工程大学密码工程学院，郑州 450001）

状态维修下通指装备可用度评估

刘欢庆，罗长远，庞松超

（解放军信息工程大学密码工程学院，郑州 450001）

随着监测诊断技术的发展，状态维修在通指装备维修中应用范围越来越广。根据系统模块之间的并联供求关系，以系统可用度求解为目标，建立多态串并联可控系统可用度精确求解模型。在对模型进行求解的过程中运用发生函数算法，对算法的运用范围进行拓展。实例结果证明评估模型的精确性，对于装备状态评估具有更强的指导性。

发生函数法，可用度评估，串并联可控系统

0 引言

通指装备的快速发展和应用，在提升我军通信保障能力的同时，也对部队维护管理工作提出更高要求，传统维修方式已不能完全满足对其进行精确维修的需求。以往应用于航空航天和导弹等价格昂贵装备上的状态维修（CBM），正逐步应用于通指装备的维修。

开展状态维修的基础在于装备状态的评估，装备状态的评估也直接影响维修间隔期和备件库存量的确定。可用度作为衡量装备系统状态的一个重要指标，经过长期的理论研究和工程实践，研究人员将复杂装备系统分解为串联、并联、r/n（G）和旁联4类，以简化对系统可用度的求解。胡林敏［1］建立了串并混联可修系统模型，给出分析具有冗余失效相关、不同设计的系统可用度计算方法和系统优化设计方案。张涛［2］针对n比较大的r/n（G）系统，提出（m，NG）维修策略，并对这种维修策略模式下的系统可用度进行了评估。Li［3］提出一种用于在非动态模式下评估加权r/n（G）系统可用度递归算法。曹畔畔［4］建立系统状态及其性能与时间之间的关系，构建多态加权k/n系统可用度的动态评估模型。Liu［5］和Ding［6］等人利用曲线拟合和通用生成函数，对设备元件状态不明确系统的可用度进行求解。另一方面，随着人们对装备系统认识的深化，对于某些复杂系统也建立了相应模型，金星［7］对共因失效系统的可靠性进行分析，Levitin［8］对总线共享型多状态系统的可用度进行了研究。

在通指装备模块供求关系中，除了以上介绍的单线串联式，并联方式更为普遍，文献［9］对该类系统进行了概括性论述，将此类系统近似为串并联模型进行研究，不能精准描述系统状态的变化。针对此问题，本文构建了多态串并联可控系统模型，对其可用度进行精确求解。

1 问题描述

状态维修在制定维修策略时，考虑系统运行的状态以及设备间由于制造过程、使用保障过程等原因造成的差异，能更精确地对装备进行维修管理。尽可能在其发生故障前进行维修，能够有效减少装备的维修时间，节约维修费用，延长使用寿命，提高装备完好率和可用度。其简要实施过程如图1所示。

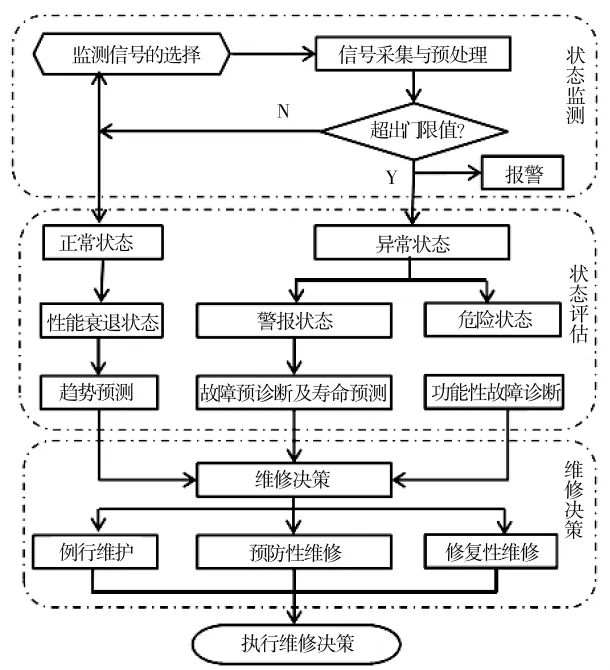
图1 状态维修的实施过程

可用度表示可维修系统在某一时刻具有或维持规定功能的能力，是对装备可靠性、维修性和保障性的综合反映，也是使用单位制订装备维修保养计划、筹划备件供应的依据。状态信息获取与状态监测建立在硬件设备的安装和调试上，而故障诊断与预测以及状态维修分析与决策离不开对装备可用度的精确求解。

鉴于通指装备的重要性，为提高其可用度，在装备设计时，对于一些易于损坏或比较关键的模块，通常采用模块冗余和容错的方法进行处理，此类方法操作简便、技术障碍小。但是单纯依靠增加模块的个数来提高系统的可用度，既不经济也不符合装备便携性和小型化的要求。这就牵涉到对多态串并联可控系统可用度的评估求解，确定模块最佳冗余和容错个数。

2 评估模型建立

2.1 符号说明

n：生产单元数目

H：供应单元数目

Bh：供应单元h的供应能力

βhi：供应单元h在状态i下的供应能力

qhi：供应单元h在状态i的概率

gj1：生产单元j的生产能力

pj1：生产单元j的可用性

wjh：单元h为单元j正常工作提供的供应值

M：系统或元件最佳运行状态

G：生产系统性能水平

Sk：生产系统集合

2.2 通用生成函数介绍

通用生成函数（UGF）是由Ushakov提出的一种用于解决离散数学领域众多问题的非常有效的运算工具。它以离散信号分析中的Z变换为理论基础，用来评估串并联多状态系统的可用度，并用于在计算资源匮乏的环境中进行冗余分配。通用生成函数具有良好的特性，如微分、积分特性等，通过这些特性可将传统积分转换为被积函数的代数多项式运算，减少计算量。

根据部件性能要求X*和部件U（z）函数就可以求得满足部件性能要求的概率 Pr为：。

由此可见，部件不确定性分布描述和失效概率近似的关键在于计算部件U函数。U函数是部件工作状态及对应状态概率的联合表达式，能反映部件性能的不确定性分布。U函数本身具有良好的特性，对于多部件系统，U变换的实质是通过逻辑关系算子实现对部件不确定性向系统不确定性的传递。

假定一个多状态性能水平系统由m个部件构成，每个部件j具有Mj+1个不同的状态，j=1,2，…，m。各个状态对应的性能水平记为，处于各状态性能水平的概率记为则部件j的通用生成函数为：

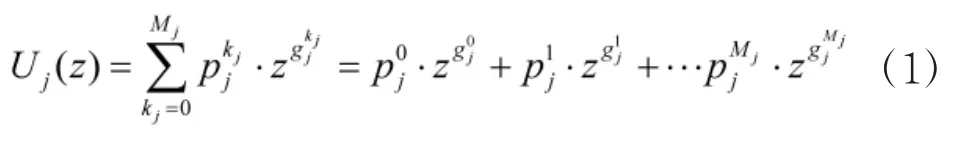
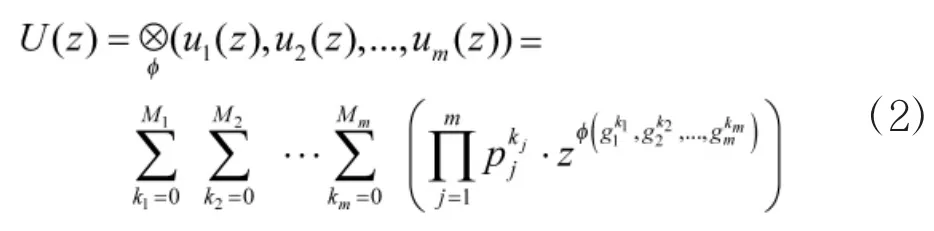
2.3 多态串并联可控系统可用度模型

假设系统由H个原料供应单元（RGSs）和n个生产单元（MPS）组成（图2）。各个单元有M+1种工作状态，当某一单元i工作在j状态时，其性能权重为wij。供应单元的状态决定生产单元的工作状态，而主控系统可以根据生产单元性能参数决定其工作状态，使得生产效率达到最优。

对于如图2所示的多态串并联可控系统，原料供应单元h的供应能力Bh的U函数可以表示为：。

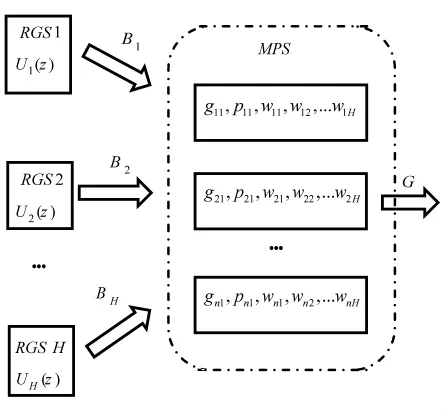
图2 多态串并联可控系统

可根据生产单元的工作与否将整个生产系统看作一个由2n个元素组成的集合S，Sk为第k（1≤k≤2n）个元素。生产系统处于k状态的概率为：

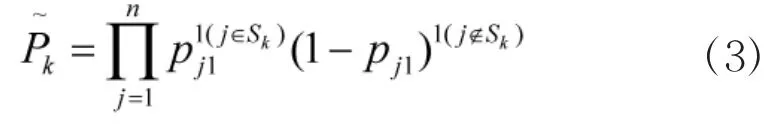
则在状态k下最大可用概率和需求最大值分别为：

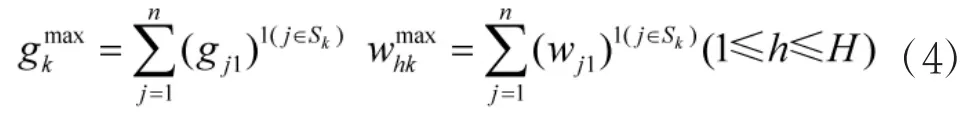
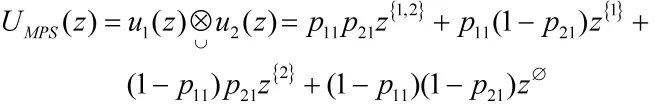
同理，对于一个由n个生产单元组成的生产系统，其U函数表达式为：

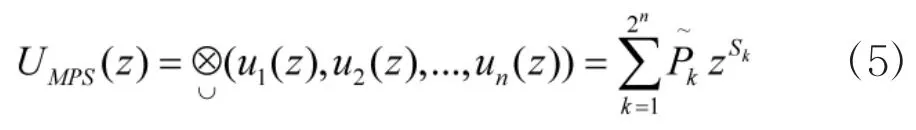
当任一供应单元的供应能力不能满足生产单元的需求时，可通过对下式线性规划方程的求解，得出使得生产系统最大化的供应单元组合。

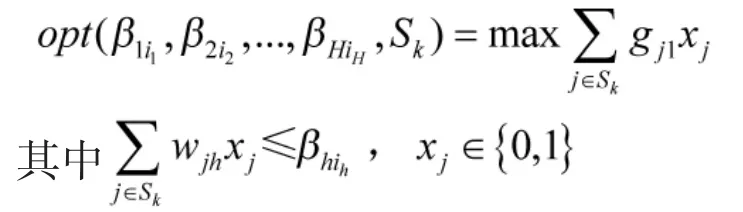
而对于整个生产系统的性能分布，可以通过综合考虑供应单元和生产单元的各种有效组合的方式来获得。对于每一种组合，上式方程的最优解代表了系统的最优性能水平。而代表整个生产系统性能水平（G）分布的U函数可以表示为：

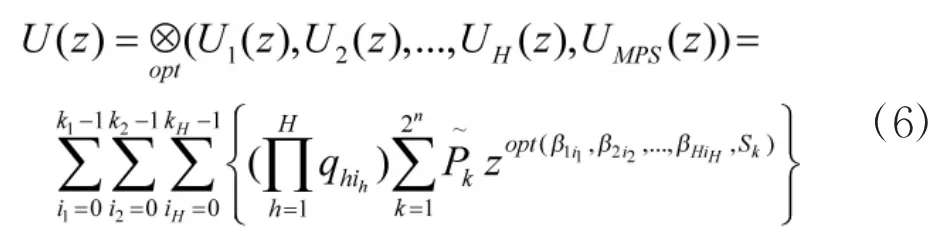
就多态串并联可控系统而言，对于门槛值ω，当系统的状态性能水平不小于ω时，系统可用，否则系统不可用。引入示性函数1（gk≥ω），当gk≥ω时函数为1（gk≥ω）=1；当gk＜ω时函数为1（gk≥ω）=0。因此，系统可用度可由下面表达式确定：

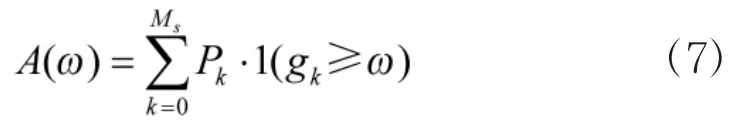
基于通用生成函数的系统可靠性指标有系统可用度A（ω）及剩余输出均值D（ω），ω为输出门槛值。

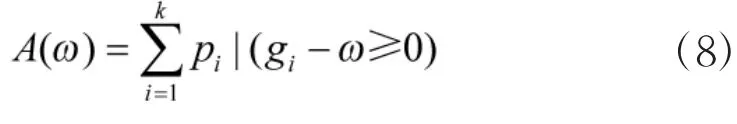
式中：当系统输出状态gi满足门槛值ω的要求时，系统能可靠完成任务的概率。

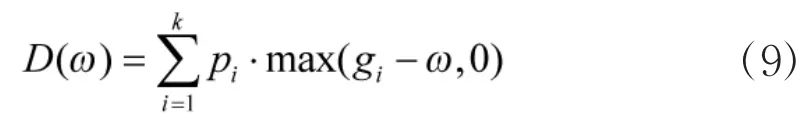
式中：D（ω）为当系统满足输出门槛值ω的要求时，系统输出余量的均值，反映系统完成任务储备能力的大小。

3 实例分析

在我军通指装备中，北斗系统在指挥控制、精确打击、态势感知、时间同步等众多领域内获得了广泛的应用。北斗用户机已广泛配发至陆、海、空、火箭军的基层部队，成为我军服务领域最广的通指装备，为我军指挥自动化、通信现代化提供了强有力的支撑。用户机的可靠性直接关系到定位功能、通信、授时等功能的实现，根据装备系统模块化集成的思想，用户机可分解为4个模块（如图3），信号处理模块中的接收通道对天线模块和射频模块构成了并联供求关系，可将其作为一个多态串并联可控系统进行研究。

假设某一款北斗用户机设计参数如下：能够同时处理3个卫星的信号，3个信号通道的处理能力和可用性分别为g11=10，p11=0.8；g21=15，p21=0.9；g31=20，p31=0.85。对于天线模块，通道的需求分别为w11=5，w21=2，w31=3。天线模块按照安全性的目的备份一个，其处理效率分别为10和6，可用性分别为0.9和0.8。针对射频模块，通道的需求分别为w12=4，w22=5，w32=7。射频模块安装两个，可同时工作，所能提供的处理效率均为9，其可用性均为0.8。

由式（5）可以得出代表天线模块、射频模块和信号处理模块能力分布的U函数分别为：

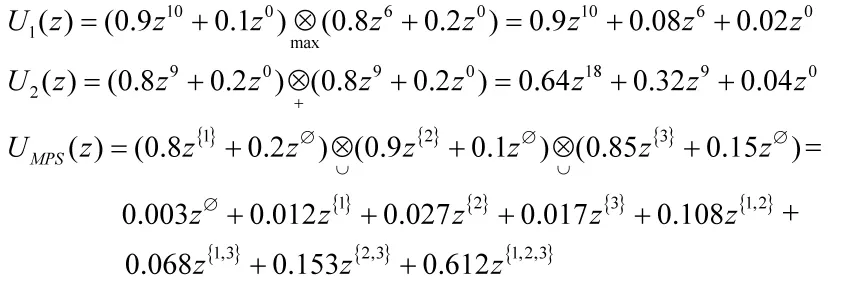
由上式可得，天线和射频模块供应能力的组合方式（B1，B2）和信号处理系统集合（Sk），如表1所示。表中包含信号处理系统最优生产能力和与之相对应的供应需求，同时表1显示了在B1和B2约束下信号处理系统的最优工作单元集合和最大生产效能（G）。

根据表1，结合式（6）可得整个信号处理系统性能水平分布的U函数：

求出整个系统性能水平分布后，便可得用户机在不同性能要求下的可用度（如图4中实线所示）。例如，当w=20时：

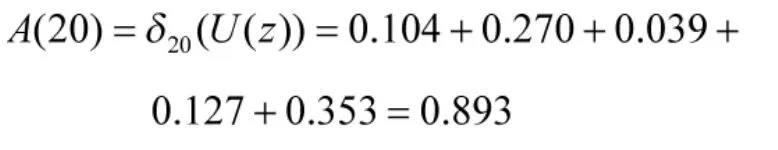
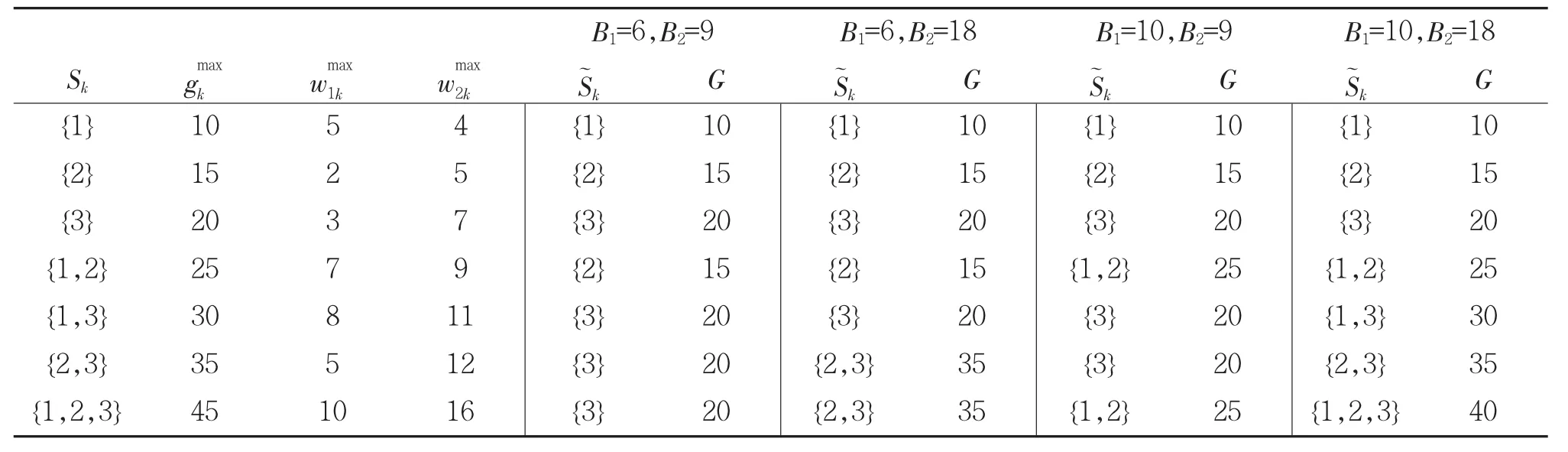
表1 用户机系统模块组合效能表

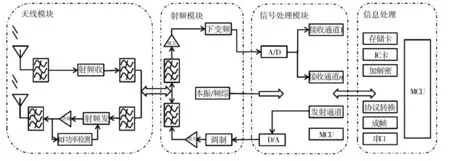
图3 北斗用户机原理框图

若按文献［9］所述方法，将用户机近似为串并联系统来进行分析，其可用度变化如图4中虚线所示，与装备的实际性能分布相比，存在较大的误差，如在区间，虚线保持在同一值，实线阶跃变化明显，实线对通指装备实际状态的描述更为贴切。

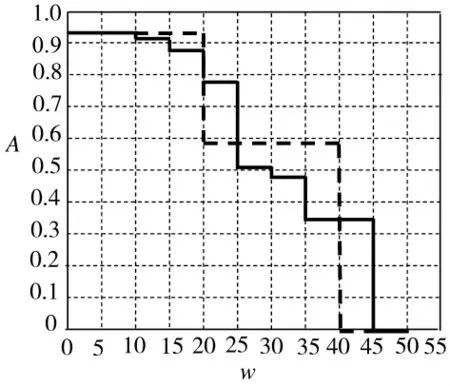
图4 用户机可用度分布图

4 结论

针对通指装备中普遍存在的模块并联供求方式，建立多态串并联可控系统可用度评估模型。实例检验结果表明，相较于以往的算法，能够更精准地描述系统状态变化，对于综合确定关键模块冗余和容错的个数具有很强的指导意义。但在实际的使用过程中，系统模块存在老龄化现象，如何在动态条件下评估此类系统的可用度，是以后研究的方向。

［1］胡林敏.串并混联可修系统的可用度分析及应用研究［D］.秦皇岛：燕山大学，2014.

［2］张涛，武小悦，郭波，等.（m，N_G）维修策略下可修系统的使用可用度模型［J］.系统工程学报，2007，22（6）：627-633.

［3］WEI L，MING J Z.Reliability evaluation of multi-state weighted k-out-of-n systems［J］.Reliability Engineering& System Safety，2008，93（1）：160–167.

［4］曹畔畔，罗长远，包记凯.多态加权k/N系统可用度动态评估模型［J］.系统工程，2015，33（3）：143-148.

［5］YU L，HONG Z H.Reliability assessment for fuzzy multi-state systems［J］.International Journal of Systems Science，2010，41（4）：365-379.

［6］YI D，MING J Z，ANATOLY L，et al.A framework for reliability approximation of multi-state weighted k-out-of-n systems［J］.IEEE Transactions on Reliability，2010，59（2）：297-308.

［7］金星，洪延姬，杜红梅.共因失效系统的可靠性分析方法［M］.北京：国防工业出版社，2008：11-15.

［8］GREGORY L.Reliability of multi-state systems with common bus performance sharing［J］.LIE Transactions，2011，43（7）：518–524.

［9］刘佳璐.串并联生产系统的模型研究［D］.天津：天津大学，2012.

Reliability Assessment of Communication Command Equipment on Condition-Based Maintenance

LIU Huan-qing，LUO Chang-yuan，PANG Song-chao
（Cryptography Engineering College，PLA Information Engineering University，Zhengzhou 450001，China）

Along with the rapid development of monitoring and diagnosis technology，conditionbased maintenance strategy surely will be the trend of communication command equipment maintenance management.According to the parallel supply-demand relationship between system components，aim for the availability，a polymorphic series-parallel controllable system availability accurate solution model is established.To use the universal generating function during the solving process，and the application of this algorithm is expanded.The results are given in the numerical example illustrate the flexibility and practicality of the mathematical model.The situation is closer to actual working conditions of communication command equipment.

universal generating function，reliability assessment，series-parallel controllable systems

TP206+.3

A

1002-0640（2017）05-0090-05

2016-03-18

2016-05-17

刘欢庆（1989- ），男，河南西华人，硕士研究生。研究方向：装备可靠性。