基于乘积偏好关系的专家模糊核聚类赋权方法*

王泽洲，陈云翔，项华春

（空军工程大学装备管理与安全工程学院，西安 710051）

基于乘积偏好关系的专家模糊核聚类赋权方法*

王泽洲，陈云翔，项华春

（空军工程大学装备管理与安全工程学院，西安 710051）

多属性、多目标性决策中，针对专家给出各方案偏好关系下的决策问题，提出一种基于乘积偏好关系的专家模糊核聚类赋权方法。该方法运用模糊核聚类的思想实现对决策专家的聚类，并通过放宽归一化约束条件，克服了传统模糊核聚类算法中离群点对聚类结果的影响。同时，在专家类内赋权过程中，运用CI-IOWG算子集结同类专家的意见，依据不同专家对于形成类别一致性意见的贡献程度来确定专家权重；克服了传统基于熵权或判断矩阵一致性的赋权方法的局限性。算例表明，该方法可行、有效。

乘积偏好关系，专家赋权，模糊核聚类，CI-IOWG算子

0 引言

在多目标、多属性决策问题中，由于决策对象存在模糊性，决策者存在主观不确定性，决策者（专家）往往偏向于给出决策对象相互比较的偏好关系。这些偏好关系大致可以分为模糊偏好关系、语言偏好关系以及乘积偏好关系3类［1-4］。当前，对于偏好关系决策问题的研究主要集中于多偏好关系单一属性决策、单一多属性偏好关系决策以及多属性群决策方向，而缺乏对于通过聚类方法分析偏好差异的研究。如徐泽水等［5］采用目标规划的方法，解决基于模糊互反判断矩阵的（乘积偏好关系）和信息不完全的决策问题当中的属性赋权问题，从而得到方案的最终排序。Herrera-Viedma等人［6］提出了一种由偏好值构成的集合来构造一致性模糊偏好关系和一致性乘积偏好关系的方法，并以此为基础集结专家意见，建立目标规划模型，确定方案排序。徐选华等［7］通过建立偏差熵模型，确定专家权重和属性权重的初始值，并通过迭代运算达到群体一致性水平，从而最终获得一个综合各方意见的群体一致性乘法偏好关系。

为了解决在乘积偏好关系下缺乏运用聚类分析的方法解决多属性、多目标决策这一问题，本文提出一种基于乘积偏好关系的专家模糊核聚类赋权方法。该方法运用核函［8-10］数将偏好关系矩阵的特征向量映射到高维特征空间，进一步发掘出了偏好关系的本质信息，实现了对专家偏好关系的聚类；同时，通过放宽传统模糊核聚类算法的归一化约束条件［11-12］，克服了当数据包含离群点时，会导致2个或2个以上聚类对象对于2个类别的隶属度十分接近，从而难以分类的情况发生，实现对离群点的准确聚类。并且在类内赋权过程中，该方法采用CI-IOWG算子［13］集结专家的意见，依据不同专家对于形成类别一致性意见的贡献程度来确定专家权重；解决了在判断矩阵一致性以及信息熵都相等但专家意见却差别很大的情况下，因采用信息熵、判断矩阵一致性比率或两者耦合作为聚类标准而导致意见不同的专家被赋予相同权重的问题，拓展了赋权方法的应用范围。

1 基于乘积偏好关系的专家模糊核聚类分析

模糊核聚类的主要原理是：通过特定的非线性函数Φ，将专家偏好矩阵的排序向量映射到高维特征空间Rd，并在特征空间Rd中对专家进行模糊聚类。通过高维映射，可以优化样本的特征，并有效提高算法的分类效果。通过引入满足Mercer条件［12］的核函数，偏好矩阵排序向量在特征空间上的点积运算即可转化为核函数的计算，而与映射函数Φ无关，从而实现更好的聚类。本文采用偏好矩阵排序向量的隶属度作为聚类依据实现对专家的分类。

假设现有M位专家对n个对象进行评价，第m位专家给出的偏好矩阵为Am，而偏好矩阵的排序向量为，。用Φ（Um），Φ（Vl）表示专家偏好矩阵排序向量Um和聚类中心Vl在高维特征空间Rd的像。本文将模糊核聚类算法中的欧式距离转化为 Euclid距离，则

本文核函数选用高斯核函数

其中，σ为高斯核函数的宽度。

高斯核函数在模糊核聚类中应用广泛。一方面，采用高斯核函数可以获得非常好的聚类效果；另一方面，采用高斯核函数有利于算法的简化。由式（2）可知，，故式（1）可简化为：

在此条件下，模糊C均值聚类算法的目标函数为：

隶属度可由下式求出：

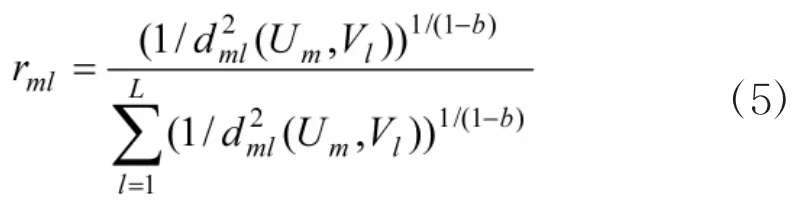
聚类中心迭代公式为：

由计算得：

隶属度迭代公式为：

基于乘积偏好关系的专家模糊核聚类方法的具体步骤为：

Step 1：按照专家给出的偏好矩阵，求出对应的排序向量Um；

Step 2：设定聚类类别数C，模糊加权指数b，高斯核函数宽度σ，最大迭代次数T以及迭代终止条件；

Step3：按照式（5）计算得出各专家偏好矩阵排序向量在高维特征空间的隶属度rml；

2 基于乘积偏好关系的专家赋权分析

本文认为，为专家赋权，一方面要考虑专家所在类别的人数，专家所在类别人数越多，相应专家权重应该越大，这正体现了少数服从多数的原则；另一方面参照多属性、多目标决策中集结专家意见形成一致性意见的原理，依据不同专家对于形成类别一致性意见的贡献程度来确定专家权重。

2.1 类间赋权分析

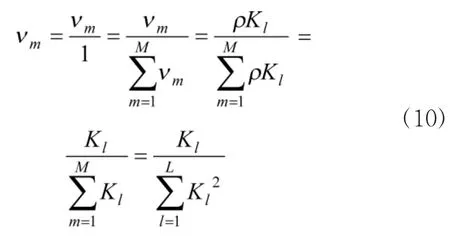
而本文认为，比例因子应该是对于每个专家不同的，即

其中，α为对每个专家都相等的与所在类别专家的人数有关的比例因子；φm与专家意见对形成所在类别一致性意见的贡献度有关，同一类专家中，不同专家的φm可能不同。由此可得

分析式（13）可知，α为对每个专家都相等的与所在类别专家的人数有关的比例因子，是影响聚类分析结果的关键因素，而φm主要对类中专家权重的差别产生细微的影响，所以应该有。则有

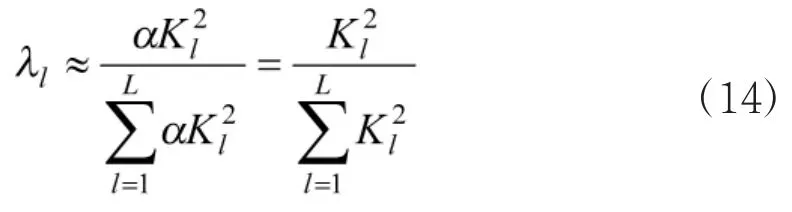
2.2 类内赋权分析

经过聚类分析，可以将意见相似的专家聚合成类。设ωlk为第l类中第k位专家的类内权重；vlk为第l类中第k位专家的总体权重。第l类专家中第k位专家针对不同方案两两比较给出的乘积偏好关系为

则定义乘积偏好关系Akl与Akg的相容度为

由式（15）可知

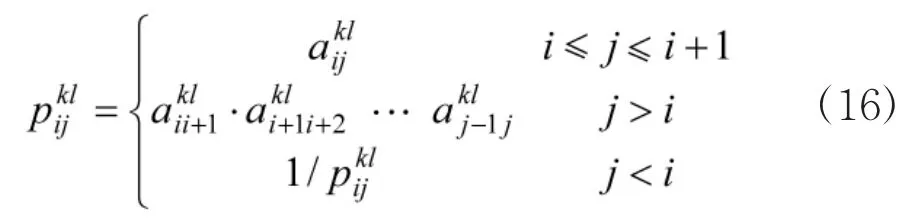
通过CI-IOWG算子集结专家的类别意见，可得

具体证明过程由文献［13］可知，在此不作证明。其中函数CI-IOWG是由产生的n维诱导有序加权几何平均算子，简记为CIIOWG算子，CI（l）为相应乘积偏好关系P（l）的诱导值。为L个二维数组，σ（l）为按从大到小顺序排列的第l个大的数的下标。ωσ（l）为对应的权值，满足。

则运用过CI-IOWG算子集结专家的类别意见，确定专家类内权重的具体步骤如下：

Step2：由式（15）得出乘积偏好关系矩阵Akl和与其相关的一致性乘积偏好关系矩阵Rkl的相容度CI（l）；

3 算例分析

为满足未来战争的需要，空军派出7位专家对3种新型歼击机的设计方案展开论证，以便确定最终设计方案。而专家（e1，e2，e3，e4，e5，e6，e7）对方案集X={x1，x2，x3}给出的偏好矩阵为：

首先，根据专家给出的偏好矩阵，计算得到对应的排序向量，采用改进型模糊核聚类法对排序向量进行聚类。为确保聚类精度符合要求并加快收敛速度，依据经验，选取初始参数为。同时由于有7位专家参与决策，因而专家类别数的取值可以为2，3，4，5，6。通过改进型模糊核聚类法对专家进行聚类分析，得到不同分类情况下专家的隶属度矩阵R*以及相应类别的聚类中心。

3.1 C=2

聚类中心为：

隶属度矩阵为：

可知第1类包含专家3、5、7，第2类包含专家1、2、4、6。聚类结果为{（3，5，7）（1，2，4，6）}。

3.2 C=3

聚类中心为：

隶属度矩阵为：

可知第1类包含专家3、5、7，第2类包含专家1、4、6，而第3类只包含专家2。聚类结果为{（2）（3，5，7）（1，4，6）}。

3.3 C=4

聚类中心为：

隶属度矩阵为：

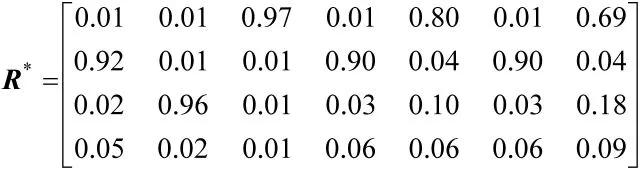
可知第1类包含专家3、5、7，第2类包含专家1、4、6，第3类包含专家2，第4类不包含任何专家。聚类结果为{（2）（3，5，7）（1，4，6）}。

3.4 C=5

聚类中心为：

隶属度矩阵为：

可知第1类不包含任何专家，第2类也不包含任何专家，第3类包含专家1、4、6，第4类包含专家2，第5类包含专家3、5、7。聚类结果为{（2）（3，5，7）（1，4，6）}。

3.5 C=6

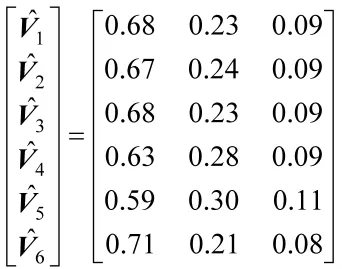
聚类中心为：

隶属度矩阵为：

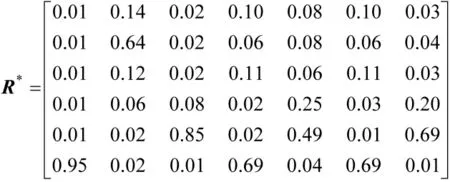
可知第1类不包含任何专家，第2类包含专家2，第3类不包含任何专家，第4类不包含任何专家，第5类包含专家3、5、7，第6类包含专家1、4、6。聚类结果为{（2）（3，5，7）（1，4，6）}。

通过分析可以发现，本文采用的聚类方法在类别数C=2时，专家1、4、6对于自身类别的隶属度要远高于专家2对于自身类别的隶属度；同时在C=3，4，5，6时，专家2明显地被单独分为一类。经过分析可以发现，专家2即为离群点，其自身对于3，5，5专家类和1，4，6专家类的隶属度很低，只是由于聚类类别数较少，难以得到理想的聚类结果，使得专家2被强制划分到专家1、4、6的类别。因而将专家分为两类是不合理的，因此，可以确定最终的聚类结果应为{（2）（3，5，7）（1，4，6）}。

依据聚类结果对专家进行赋权分析。根据式（14）可得专家的类间权重分别为：

依据2.2节提出的类内赋权法确定专家类内权重。

第2类专家包含专家3，5，7。运用式（16）得到专家3，5，7给出偏好矩阵对应的一致性互反判断矩阵：

通过分析可以发现，专家5给出的偏好关系通过式（16）得到的互反判断矩阵不满足1～9标度要求，其中有元素的取值超出了［1/9，9］范围。因而需要通过转换公式转换得到与专家3，5，7给出的乘积偏好关系相一致的一致性乘积偏好关系：

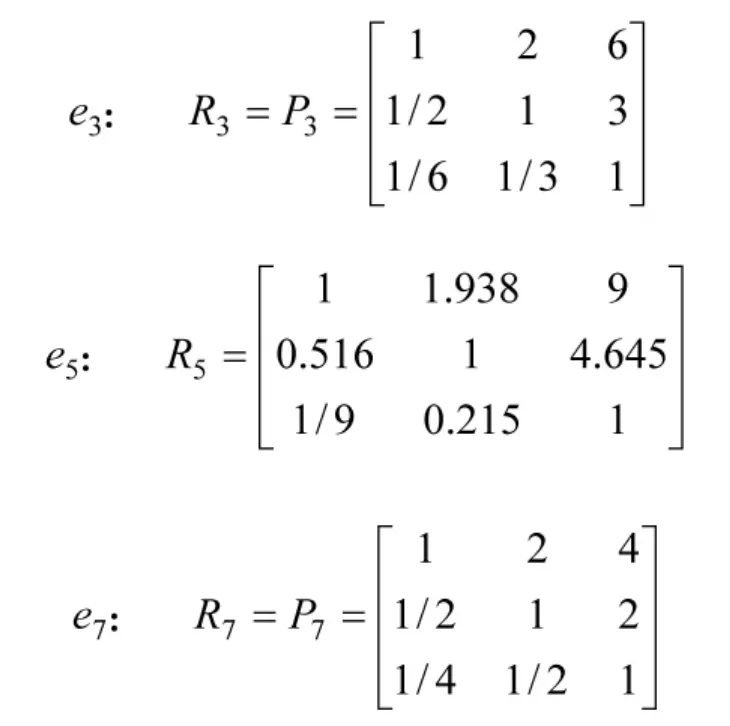
由式（15）可得专家3，5，7给出的偏好关系A3，A5，A7与对应的一致性乘积偏好关系R3，R5，R7的相容度分别为：

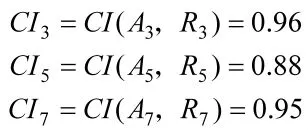
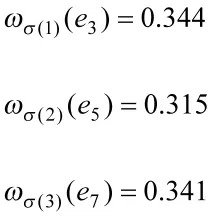
同理可得专家1，4，6的类内权重为

最后，由式（21）得到专家总体权重为

通过算例分析可以发现，采用放宽归一化约束条件的模糊核聚类方法可以克服离群点对聚类结果的干扰，使得聚类结果更加合理准确；此外，在类内专家赋权过程中运用CI-IOWG算子集结专家的类别意见，直接使用专家对自身类别的聚类贡献度作为类内权重，克服了依据一致性比率和信息熵为专家赋权的局限性。

4 结论

针对基于偏好关系的多目标、多属性决策问题，提出一种基于乘积偏好关系的专家模糊核聚类赋权方法。一方面创新运用聚类分析的思想解决基于偏好关系的决策问题，采用放宽归一化约束条件的模糊核聚类算法来削弱离群点对聚类结果的影响；另一方面运用CI-IOWG算子集结专家的类别意见，实现对专家的准确赋权。算例表明，本文所提方法可行有效。

［1］CHICLANA F，HERRERA-VIEDMA E，HERRERA F，et al. Induced ordered weighted geometric operators and their use in the aggregation of multiplicative preference relations［J］. International Journal of Intelligent Systems，2004，19：233-255.

［2］ENRIQUE H V，FRANCISCO C，FRANCISCO H.Group decision-making model with incomplete fuzzy freference relations based on additive consistency ［J］.IEEE Transactions on Fuzzy Systems.Man and Cybernetics，2007，37：176-189.

［3］XU Z S.A method based on linguistic aggregation operators for group decision making with linguistic preference relations

［J］.Information Sciences，2004，166：19-30.

［4］ALONSO S，CABRERIZO F J，CHICLANA F，et al.Group decision making with incomplete fuzzy linguistic preference relation［J］.International Journal of Intelligent Systems，2009，24：201-222.

［5］徐泽水，赵华.偏好信息为模糊互反判断矩阵的模糊多属性决策法［J］.模糊系统与数学，2004，18（4）：115-121.

［6］HERRERA-VIEDMA E，HERRERA F，CHICLANA F，et al. Some issues on consistency of fuzzy preference relations［J］. European Journal of Operational Reasearch，2004，154：98-109.

［7］徐选华，周声海，周艳菊，等.基于乘法偏好关系的群一致性偏差熵多属性群决策方法［J］.控制与决策，2014，29（2）：257-262.

［8］高新波.模糊聚类分析及其应用［M］.西安：西安电子科技大学出版社，2004：1-129.

［9］李国正，王猛，曾华军.支持向量机导论［M］.北京：机械工业出版社，2004：1-123.

［10］伍忠东，高新波，谢维信.基于核方法的模糊聚类［J］.西安电子科技大学学报（自然科学版），2004，31（4）：533-537.

［11］SCHOLKOPF B，SMOLA J，MULLER K R.Nonlinear component analysis as a kernel eigenvalue problem［J］. Neural Computation，1998，10（5）：1299-1319.

［12］章森，朱美玲，侯光奎.改进的模糊核聚类算法［J］.北京工业大学学报，2012，38（9）：1408-1411.

［13］单秀生.一些基于CI-IOWG算子的乘积偏好关系群决策的讨论［D］.合肥：安徽大学，2012.

Method of Expert Fuzzy Kernel Clustering Weighting Based on
Multiplicative Preference Relations

WANG Ze-zhou，CHEN Yun-xiang，XIANG Hua-chun
（School of Equipment Management and Safety Engineering，Air Force Engineering University，Xi’an 710051，China）

Within the multiple attributes and multi-objective decision making problems，for the case that each decision maker has a preference relation referring to alternatives，a method of expert fuzzy kernel clustering weighting based on multiplicative preference relations is proposed，in which the experts are classified by using fuzzy kernel clustering principle.By loosening the normalization constraints，the effects of outliers on the clustering results could be overcome.At the same time，this paper presents CI-IOWG operator for group decision-making with multiplicative preference relation in the process of determining the intra class weight.And the weighting method can determine the experts’weight according to the contribution degree for clustering which overcomes the limitations of the traditional weighting method based on entropy and consistency.The example shows that the method is feasible and effective.

multiplicative preference relation，experts’weights，fuzzy kernel clustering，CI-IOWG operator

C934

A

1002-0640（2017）05-0056-07

2016-03-09

2016-06-07

“十二五”国防预研基金资助项目（51327020104）

王泽洲（1992- ），男，山西长治人，硕士。研究方向：装备发展战略与管理决策。