某军用越野车转向系统结构件的可靠性设计与验证

田豪，沈阿荣，王琳，王磊

（陕西重型汽车有限公司，陕西 西安 710200）

某军用越野车转向系统结构件的可靠性设计与验证

田豪，沈阿荣，王琳，王磊

（陕西重型汽车有限公司，陕西 西安 710200）

以某军用越野车为例，通过运用可靠性设计方法，以零件无限疲劳寿命为可靠性设计原则对其转向系统关键结构件进行结构设计和疲劳寿命校核，并根据实车测得的载荷谱对零件进行台架疲劳试验，验证了可靠性设计方法的有效性。

可靠性设计；结构设计；疲劳寿命校核；疲劳试验

CLC NO.: U463.4 Document Code: A Article ID: 1671-7988 (2017)10-193-04

前言

对于汽车来说，可靠性与人身安全、经济效益密切相关。汽车由各总成、部件、零件构成，如果某一个零件损坏、一个元件失效，都可能造成事故，引起严重的后果。转向系统作为整车的关键系统之一，若转向节臂、转向摇臂等关键结构件失效可能导致车辆失去方向控制能力，进而危及车辆及驾乘人员安全，因此转向系统的关键结构件主要以无限疲劳寿命为可靠性设计目标。本文以某军用越野车一桥中间转向摇臂设计为例，通过对其进行有限元分析和疲劳寿命校核，结合试验验证，确保零件满足可靠性要求。

1、可靠性设计

1.1 结构件可靠性设计方法

结构件可靠性设计方法如图1所示。

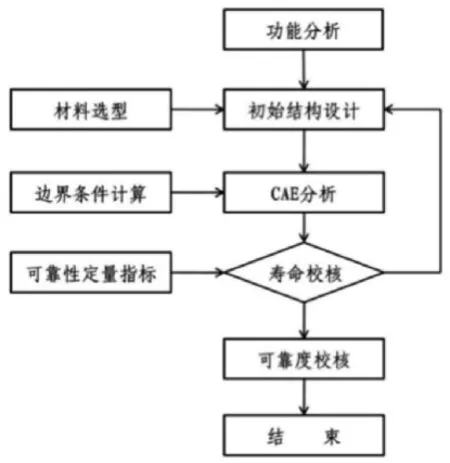
图1 结构件可靠性设计方法

1.2 初始结构设计

某军用越野车转向系统的三维布置图如图2所示，以一桥右中间转向摇臂为例进行可靠性设计。在初始设计时，参考同类车型中间转向摇臂的形状和断面尺寸，并按照轴荷等比例加强，得到一桥右中间转向摇臂结构如图3所示。

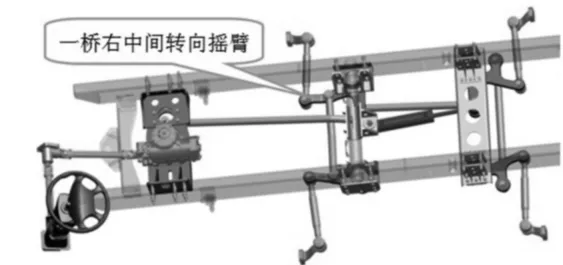
图2 转向系统三维布置图

图3 摇臂初始结构

考虑到后期批量生产的工艺性以及成本因素，中间转向摇臂的材料选用车辆锻件常用材料40Cr，按照批量生产的40Cr锻件的加工工艺及热处理工艺进行零部件加工及疲劳寿命预测。

1.3 结构应力分析

根据转向系统受力情况，建立一桥右中间转向摇臂的有限元分析模型，并进行静强度分析，优化结构后，摇臂的应力分布情况及最大应力点如图4所示。

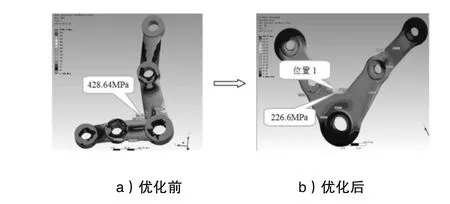
图4 一桥右中间转向摇臂结构应力分布

由于零件的疲劳破坏都是从应力集中部位处起始的，故重点校核位置1处的疲劳极限。零件在实际工作中受力状况为变幅载荷受力，为计算方便并根据一桥中间转向摇臂运动状态，位置1处所受应力状态近似为对称循环受力（应力比r=-1），此假设的受力状况比实际受力更苛刻。

1.4 疲劳寿命校核

中间转向摇臂作为转向系统的关键部件，应以无限疲劳寿命为可靠性设计目标。根据基本假设，采用常规疲劳设计方法：名义应力法。对于对称循环受力，中值（可靠度50%）无限疲劳寿命（N=107）设计采用如下公式：

经调制处理的40Cr锻件，硬度为220HB～250HB，表面经喷丸强化处理。根据热处理工艺可知抗拉强度=940 MPa，疲劳极限=422MPa（材料中值疲劳寿命）。

根据公式：

式中：Kσ为正应力下的疲劳缺口系数；q为缺口疲劳敏感度；Kt为理论应力集中系数。

对于图4中位置1处受力情况，可近似简化为L型板受弯矩的情况，理论应力集中系数使用图5近似模型计算。

图5 位置1处简化模型

根据Neuber公式：

式中：σ'为Neuber参数，可由Neuber参数图查出；σ为缺口半径(mm)；

根据文献[2]，以及多年来相同工艺40Cr锻件的疲劳试验情况，将所需技术参数代入计算公式，可得：

由于转向臂表面经喷丸强化处理，对于存在缺口的钢制试样，疲劳强度提高≮30%，对于光滑试样≮10%。β3为强化系数，修正σ-1D，这里仅取下限β3=1.1，则：

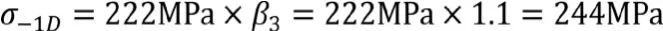
对于位置1处，一桥右中间转向摇臂极限受力时，最大应力为226.6MPa＜σ-1D，可见在比该零件实际受力更严苛的情况下，位置1处的受力也不大于此处的中值无限寿命疲劳强度。

1.5 可靠度计算

无限寿命下疲劳强度可靠性设计采用经典的P-S-N线图演算疲劳强度可靠度。为得到零件的P-S-N曲线，记应力循环数N0=103对应的有限疲劳寿命为σ-1DN。只要计算出σ-1DN，便可绘制出零件的中值疲劳寿命曲线，再计算出各自疲劳寿命的标准差，即可根据失效率P绘制出不同可靠度下的P-S-N曲线，可方便的查出零件在指定循环次数下不失效的可靠度。一般认为在循环次数N≥106，可靠度≮95%时，就认为该零件具有无限疲劳寿命。

根据零件无限疲劳寿命（N=107）时，疲劳强度为σ-1D=244MPa。

可令N≥107，疲劳强度均值：

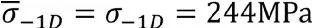
当N= N0时，疲劳强度均值：

在材料的近似S-N曲线的基础上，通过计算N=107，N= N0时的疲劳强度均值，描点连成该零件的近似中值疲劳（S-N）曲线，见图6。

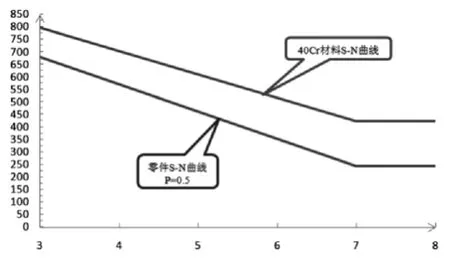
图6 材料S-N曲线及零件S-N曲线

注：图中横坐标表示应力循环次数N，例如3代表N=103次；

纵坐标表示对应不同应力水平的疲劳极限（单位为MPa）。

当N≥107，零件疲劳强度标准差：

当N≥107，不同失效概率P下的零件疲劳强度：

式中：Zp为标准正态分布临界值；

对应于不同失效概率时，Zp值如表1所示。

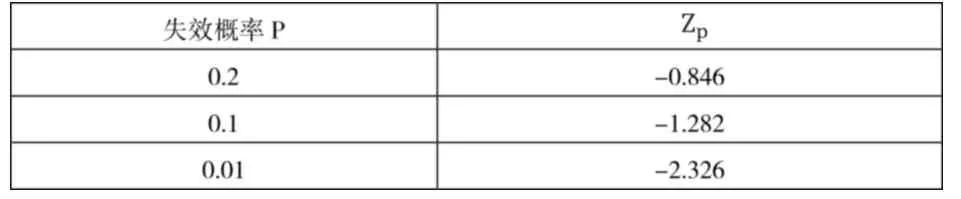
表1 标准正态分布不同失效概率下的Zp值

在材料及零件的中值疲劳（S-N）曲线的基础上，使用上述数值描点，将相同失效概率下的点用直线连接，即可获得零件的近似P-S-N曲线，如图7所示。

图7 零件P-S-N曲线（坐标含义同图6）

根据静态极限受力分析，在位置1处最大应力为226.6MPa，实际中的零件在循环次数N＞106时即为零件的无限疲劳寿命，由图7查得：在接近N=107时，此点近似在P=0.1的S-N线上，故零件不疲劳失效的可靠度R=0.99，即在此对称循环应力下，零件不疲劳破坏的可靠度为99%，所以理论上一桥右中间转向摇臂是满足设计要求的。

2、可靠性试验验证

通过在一桥右中间转向摇臂上贴应变片采集载荷谱（见图8），并通过换算获取该件位置1处在特殊路段的载荷-时间历程。车辆在工作时直接测得的载荷-时间历程为零件的工作谱，由于随机载荷循环的不确定性，此谱无法直接使用，为理论分析及试验方便，利用雨流计数法将其处理成一系列的全循环或半循环，从而获得最大应力循环。初步处理后的载荷-时间历程如图9所示。

图8 载荷谱采集

图9 初步处理后的载荷-时间历程

雨流计数法处理后的最大应力循环如图10所示。

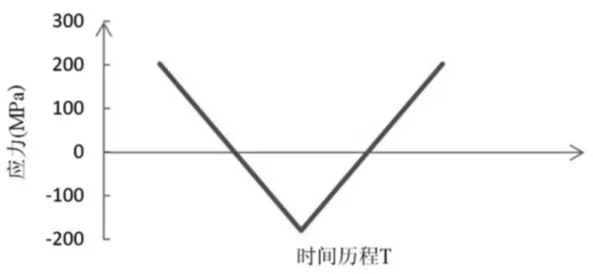
图10 雨流法处理后载荷谱中最大应力循环

由处理后的图10可以看到，该零件在实际工作时，最大的载荷循环为：

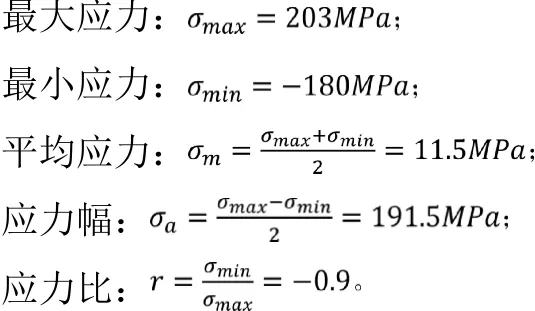
可见该零件所受最大变幅应力为非对称循环变应力，为理论及实际试验方便，处理成对称循环变应力的形式，令其最大应力σmax保持不变，。该处理后的零件受力比实际受力更为苛刻，故利用此数据进行的试验可靠性有充分的保证，试验结果可信。

运用成组法进行疲劳试验，一桥右中间转向摇臂台架试验情况如图11所示。结果显示在N=106次循环下，该零件未破坏，即该零件设计的可靠性是符合要求的。

图11 一桥右中间转向摇臂台架试验

3、结论

在转向系统设计过程中，对结构件进行初始结构设计，通过静强度分析找出零部件的薄弱环节或应力最高的危险点，采取相应措施进行优化，并对零部件进行疲劳寿命校核和试验验证，确保关键零部件满足可靠性要求。通过理论计算，结合试验验证情况，说明了可靠性设计方法在零部件设计中的有效性。

[1] 王霄锋编著.汽车可靠性工程基础[M].北京:清华大学出版社, 2007.

[2] 赵少汴,王忠保编著.抗疲劳设计[M].北京:机械工业出版社,1997.

[3] 刘惟信主编.汽车设计[M].北京：清华大学出版社,2000.

[4] 明平顺,李晓霞编著.汽车可靠性技术[M].北京:人民交通出版社,2004.

Structure Reliability Design and Verification of a Military Off-road Vehicle Steering System

Tian Hao, Shen Arong, Wang Lin, Wang Lei
（Shaanxi Heavy Duty Automobile Co., Ltd, Shaanxi Xi’an 710200）

In this paper, a military off-road vehicle is taken as an example. By using reliability design method, based on the reliability design principle of infinite fatigue life, the structural design and fatigue life check of a key component of the steering system are carried out. According to the measured load spectrum, the bench fatigue test of the part was carried out. and the validity of the reliability design method is verified.

reliability design; structural design; fatigue life check; fatigue test

U463.4

A

1671-7988 (2017)10-193-04

10.16638/j.cnki.1671-7988.2017.10.067

田豪，就职于陕西重型汽车有限公司。