分数阶Klein-Gordon-Schrödinger方程弱解的存在性

赖满丰，金玲玉

（华南农业大学数学系，广东广州510642）

分数阶Klein-Gordon-Schrödinger方程弱解的存在性

赖满丰，金玲玉*

（华南农业大学数学系，广东广州510642）

考虑满足一定条件的分数阶Klein-Gordon-Schrödinger方程的初值问题，并采用先验估计及Galerkin方法得到问题解的存在性。

分数阶Klein-Gordon-Schrödinger方程；弱解；先验估计；Galerkin方法

本文考虑如下一类全空间上R3×R+的分数阶方程

其中，ψ是复函数，φ，θ是实函数，v，γ，δ均是正常数，f和g是关于空间x的动力项函数。

不失一般性，空间和范数的记号与通常意义相同。Hs为标准的分数阶Sobolev空间［1］，记H=L2（R3），且用‖·‖和（·，·）表示L2（R3）上的范数和内积。对于1≤p≤∞，记‖·‖p为L2（R3）范数（‖·‖2=‖·‖）。

本文的主要结果是：

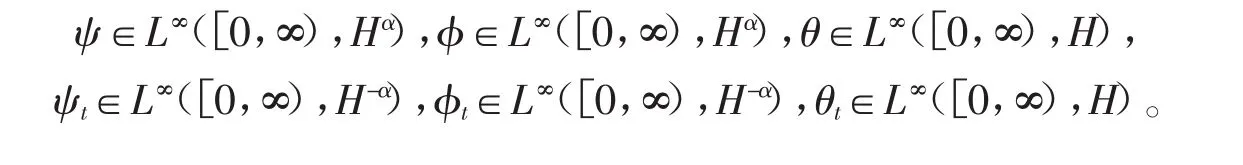
1 先验估计

引理1 若f∈H，则问题（1）～（4）的解ψ满足

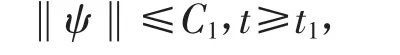
其中，常数C1依赖于v和‖f‖；t1依赖于v、‖f‖和R（这里‖ψ0‖≤R）。

证明 将方程（1）与ψ在空间H上做内积，并取其虚部，得

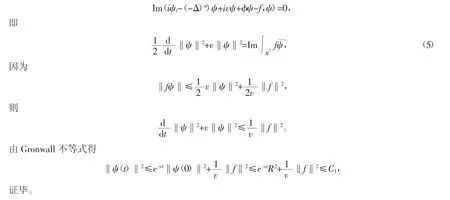
引理2若f∈H，g∈H，则存在常数δ1，使得当δ≤δ1时，问题（1）～（4）的解（ψ，φ，θ）满足

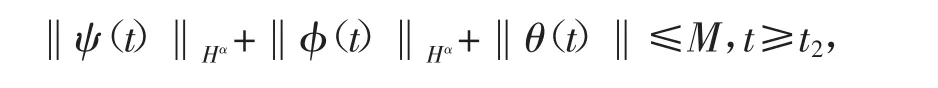
其中M依赖于（v，γ，δ，‖f‖，‖g‖），t2依赖于（v，γ，δ，‖f‖，‖g‖）和R（ψ0∈Hα≤R，φ0∈Hα≤R，θ0∈H≤R）。

证明 在空间H上，将方程（1）与-ψt做内积，得

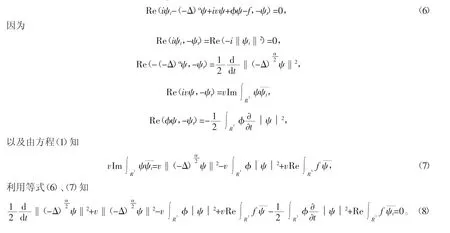
对空间Hα×Hα×H中的解进行估计，可转化为对方程（14）的每一项进行讨论。

首先令正常数δ1，使得当δ≤δ1时，有

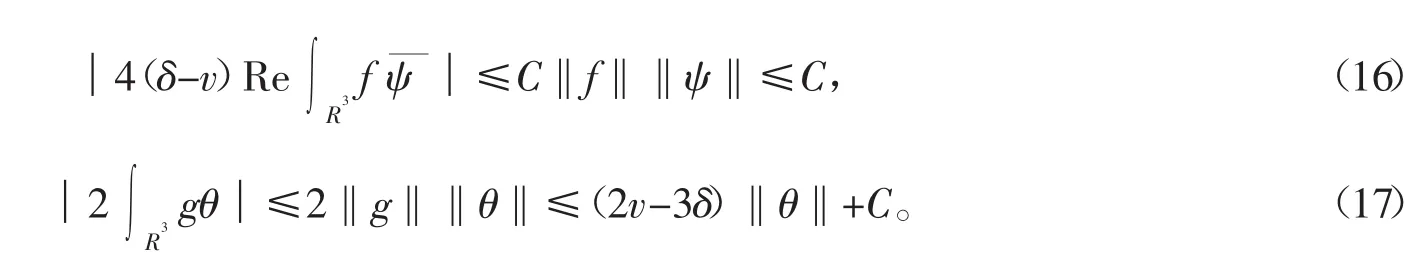
根据方程（13）～（17）可得

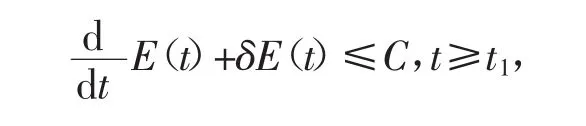
这里的t1满足引理1。则由Gronwall引理易证得引理2成立。

2 解的存在性

下面给出方程（1）～（4）弱解的存在性证明。

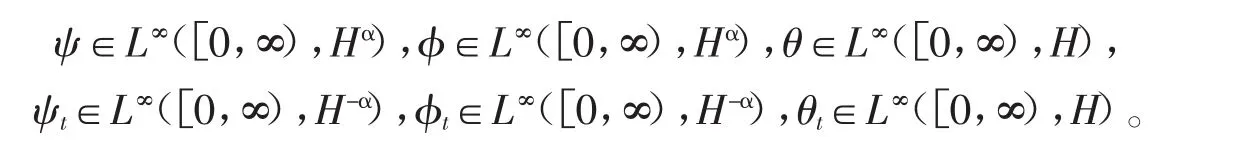
证明 下面分三步来完成定理1的证明。

第1步：利用Faedo-Galerkin方法构建逼近解。

固定一个正整数s，记

此时方程（19）～（24）是一组常微分方程组。利用标准常微分方程理论可知，当t＞0时，方程（19）～（24）存在唯一的解。

第2步：先验估计。

由引理1和引理2可知

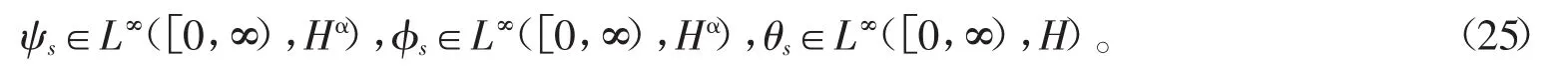
对任意的φ∈Hα（Rn），有

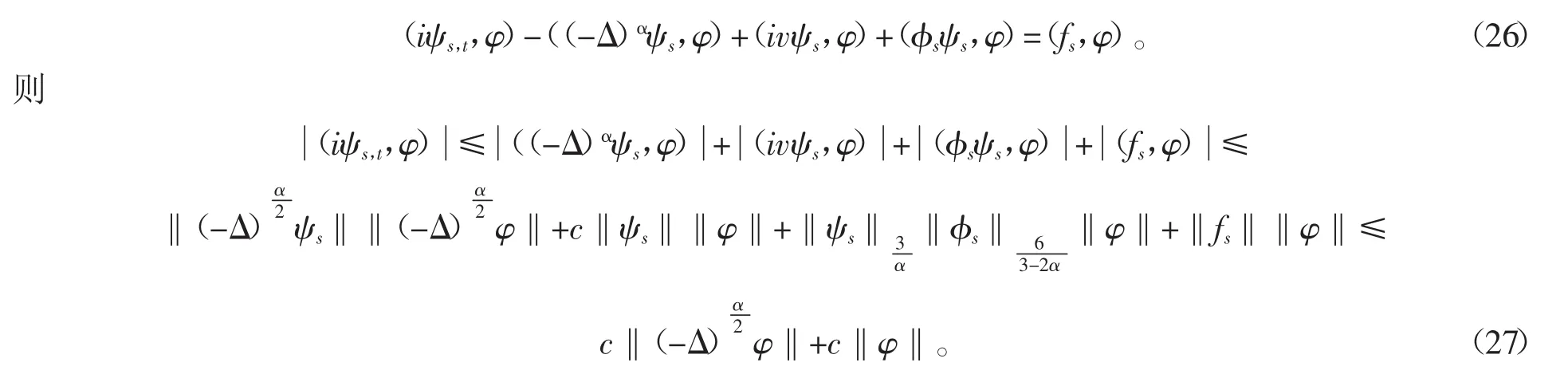
从而，由等式（26）和不等式（27）可知

故知ψ（0）=ψ0。同理可得φ（0）=φ0。

综上所述，定理1得证。

3 结论

在本文中，主要讨论了分数阶Klein-Gordon-Schrödinger方程，对整数阶的方程进行了拓展，在参数满足的假设条件下，得到了其弱解的存在性。文章主要采用能量方法、利用插值不等式得到先验估计，采用Galerkin方法得到解的存在性。下一步笔者将对该方程解的性质进行研究。

［1］LU K,WANG B.Global Attractors for the Klein Gordon Schrödinger Equation in Unbounded Domains［J］.Journal of Differential Equations,2001,170（2）:281-316.

［2］PARK J Y,KIM J A.Maximal Attractors for the Klein-Gordon-Schrödinger Equation in Unbounded Domain［J］.Acta Applicandae Mathematicae,2009,108（2）:197-213.

［3］T’EMAMR.Infinite Dimensional Dynamical Systems in Mechanics and Physics Springer Verlag［J］.Applied Mathematical Sciences,1997,18（5）:2135-2143.

［4］BALL J M.Global attractors for damped semilinear wave equations［J］.Discrete&Continuous Dynamical Systems,2003,10（1-2）:31-52.

［5］LANGE H,WANGB.Regularityofthe Global Attractor for the Klein-Gordon-Schrodinger Equation［J］.Mathematical Methods in the Applied Sciences,1999,22（17）:1535-1554.

［6］GUO B,DU X.Existence of the Periodic Solution for the Weakly Damped Schrodinger-Boussinesq Equation［J］.Journal of Mathematical Analysis&Applications,2001,262（2）:453-472.

［7］郭柏灵,蒲学科,黄凤辉.分数阶偏微分方程及其数值解［M］.北京:科技出版社,2011:99-120.

［8］郭柏灵.非线性边值问题的一些解法［M］.汪礼礽,译,广州:中山大学出版社,1989:335-340.

［9］郭柏灵,苗长兴.Klein-Gordon-Schrödinger方程解的整体存在性及其渐近性［J］.中国科学:数学、物理学、天文学、技术科学,1995,38（7）:705-714.

【责任编辑：王桂珍 foshanwgzh@163.com】

The existence of weak solution of fractional order Klein-Gordon-Schrödinger equation

LAI Man-feng,JIN Ling-yu
（Department of Mathematics,South China Agricultural University,Guangzhou 516042,China）

In this paper,we analyses the fractional order of Klein-Gordon-Schrödinger equation for the initial boundaryvalue problems.We use prior estimation and the Galerkin method toget the existence ofthe solution.

the fractional order of Klein-Gordon-Schr ödinger equation;weak solution;prior estimate; Galerkin method

O175.2

A

1008-0171（2017）03-0013-06

2016-10-12

国家自然科学基金资助项目（11101160）；广东省自然科学基金资助项目（2016A030313390）

赖满丰（1991-），女，广东河源人，华南农业大学硕士研究生。通信作者：金玲玉（1979-），女，湖北荆州人，华南农业大学副教授。