一种基于矩阵理论的多图组合变换研究
2017-06-15侯海平
侯海平
(安徽财贸职业学院 安徽合肥 230001)
一种基于矩阵理论的多图组合变换研究
侯海平
(安徽财贸职业学院 安徽合肥 230001)
文章结合几何变换中的矩阵理论,分析了图形变换中平移、缩放、旋转的理论基础;研究了如何使用WPF中图形变换的相关类以及辅助类解决图形变换问题;重点分析了多图组合的变换操作,提出相应的变换方案。
矩阵;图形变换;多图组合;WPF
在计算机动画和计算机辅助设计领域中经常会对虚拟场景中的物体进行各种操作,目的在于更好地观察物体本身,发现物体本身内部结构和原理。这些操作包括改变它的位置、改变它的大小、改变它的角度等[1]。准确地说这些操作也就是对图形进行平移、旋转、缩小或放大等变换[2]。
一、几何变换在图形设计中的应用
所谓几何变换就是将图形由一个几何图形变换到另一个图形,所有的图形都是由点线面构成,而这些点线面也可以相互转换,通过转换可以将面转换成线,再将线转换成点,最终每一个图形也就由若干个点构成,这些点的集合就构成了图形最基本的元素[2]。所以图形的变换也就是具体点的变换,包括了平移、缩放、旋转。
(一)平移。在二维坐标中有点(x,y),假设要对该点进行水平方向移动a个单位长度,垂直方向移动b个单位长度,则该点新的坐标为(x1,y1),其中x1=x+a,y1=y+b,这就是一个平移模型[3]。
(二)缩放。缩放操作中,通常会指定一个缩放比例,假定水平方向缩放比例为Sx,垂直方向缩放比例为Sy。在二维维坐标中有点(x,y),现在要进行缩放操作,经过缩放后则该点新的坐标为(x1,y1),其中x1=xSx,y1=ySy,这就是一个缩放模型[4]。
(三)旋转。旋转操作中,要设定2个前提,第一个为旋转的围绕点(通常为坐标原点),第二个为旋转角度θ(按逆时针旋转)。在二维坐标中有点(x,y),假设要对该点进行围绕坐标原点旋转 θ 度,则该点新的坐标为 (x1,y1),其中x1=xcosθ-ysinθ,y1=xsinθ+ycosθ,这就是一个旋转模型[5]。
二、几何变换中的矩阵理论
无论是平移、缩放还是旋转,这些变换都可以表示为矩阵计算的形式,通过矩阵的相乘构造出更复杂的变换[6]。所有的基本变换(平移、缩放和旋转)又都可以表示为普通的矩阵形式:
P’=M1·P+M2
其中P’和P表示向量,矩阵M1是一个2×2的矩阵,M2表示平移项。为了能够将二维几何变换的乘法和平移项组合成单一矩阵,必须将二维坐标(x,y)扩充到三维来表示,也就是齐次坐标(x,y,h),h是一个齐次参数[1]。
这样对于图形中每一个点就可以扩充为一个单位三维坐标,用矩阵表示就是[x y 1]。一个图形的点集就可以表示为

则设变换矩阵为T,就需要将其转换成3×3的矩阵,即

图形的变换可以表达为点集与变换矩阵的乘积,结果为变换后的图形点集矩阵,表示为

(一)平移。将T矩阵中a设定为1,b设定为0,c设定为0,d设定为1。对于点(x,y)来说就是上式中第一行的计算结果为[x+ey+f1]一行三列的矩阵,前两项就是平移后的坐标(x+e, y+f)。e表示x方向平移量,f表示y方向平移量。
(二)缩放。将T矩阵中b、c、e、f均设定为0。对于点(x,y)来说上式第一行的计算结果则为[axdy1]一行三列的矩阵,前两项就是缩放后的坐标(ax,dy)。其中a表示x方向的缩放比例,d表示y方向的缩放比例。
(三)旋转。将T矩阵中e、f均设定为0。由于需要设定2个前提,参考前文。对于点(x,y)按原点逆时针旋转θ度,按上式进行计算,结果为[ax+cybx+dy1]一行三列的矩阵,前两项就是平移后的坐标 (ax+cy,bx+dy)。那么a=cosθ,b=sinθ, c=-sinθ,d=cosθ。
三、WPF中的图形变换策略
WPF是WindowsPresentationFoundation的缩写,它是一个Windows的图形显示框架,使用WPF可以简化开发人员的开发过程,提高开发效率,并且能够比较方便的调用Windows较为底层的图形接口,WPF很好地结合了DirectX图形加速方案,使用WPF开发的软件显示效果绚丽且性能良好。
(一)图形变换相关类。为了能够方便对图形进行操作处理,WPF提供了较多的图形变换类。针对之前介绍的平移变换、缩放变换、旋转变换分别提供了TranslateTransform类、ScaleTransform类、RotateTransform类,这些类都是有关矩阵理论在变换中运用的具体形式。具体说明如表1所示。

表1 图形变换类
实际的开发过程中往往包含了多种变换形式,既可能是其中一种变换形式也可能是多种变换形式的叠加,这就要求每一个图形都支持以上三种变换类,为了能够较好的支持开发,WPF还提供了一个TransformGroup类,该类支持所有的变换形式,可以看成是各种变换形式的集合,支持多个变换的叠加。同时,为了在复杂变换过程中简化开发代码,WPF还开放了最原始的由矩阵理论支撑的MatrixTransform类。具体说明如表2所示。

表2 图形变换辅助类
(二)使用图形变换类。通常是先获取变换对象,再通过变换对象获取TransformGroup类,这样就获取了变换实例的集合。在对该集合进行处理过程中,可以通过TransformGroup类的Children属性来获取该集合,再使用Add方法和
Remove方法对集合元素进行操作。
1.TranslateTransform类的使用。
TranslateTransformtt=newTranslateTransform();//构造平移变换
tt.X=5;//传入X轴平移量
tt.Y=10;//传入Y轴平移量
group.Children.Add(tt);//添加到变换集合中
其中group为变换对象的TransformGroup类实例。本段代码执行后将会看到图形由原位置,向右移动5个像素,向下移动10个像素。如图1所示。

图1平移图形

图2缩放图形
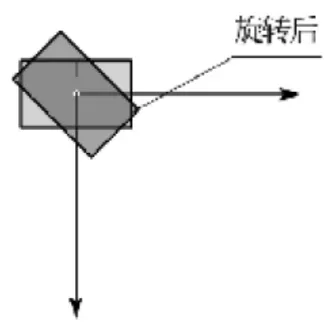
图3 旋转图形
2.ScaleTransform类的使用。
ScaleTransform st=new ScaleTransform ();//构造缩放变换
st.ScaleX=1.2;//传入X轴缩放比例
st.ScaleY=1.2;//传入Y轴缩放比例
group.Children.Add(st);//添加到变换集合中
该段代码表示将放大图片。执行本段代码将会看到图形在原位置放大1.2倍。如图2所示。
3.RotateTransform类的使用。
RotateTransform rt=new RotateTransform();//构造旋转变换
rt.Angle=45;//传入逆时针旋转的度数
group.Children.Add(rt);//添加到变换集合中
该段代码表示图形将围绕原点按逆时针方向旋转。执行本段代码将会看到图形在原位置旋转了45度。如图3所示。
四、多图组合变换
WPF是通过Canvas来呈现图形的,每一个图形显示在Canvas中的位置取决于图形距离Canvas边界最上边和最左边的距离。我们可以把离开上边的距离看成y轴坐标,与传统坐标所不同的是y轴的方向向下,距离最上边越远,y值越大。所以对于任何图形通过设置Canvas.Left和Canvas.Top,就相当于将图形定位到Canvas的坐标系中,Canvas.Left相当于水平方向的x坐标,Canvas.Top相当于垂直方向的y坐标。在做具体的图形变换时,我们只需要按照图形的中心点进行变换即可。当图形的中心点确定后,整个图形的位置就确定了。
在进行平移操作时,只需平移中心点,依据原有中心点,根据平移量计算出新的中心点位置,就能重新将图形移动到想要的位置,此时图形的宽和高无需做任何变化。
在进行缩放操作时,我们可以将图形先移动至Canvas原点,根据缩放系数计算出图形新的宽和高,当图形在原点缩放成功后,再进行一次平移,将图形移动到原位置,就完成了图形在Canvas中的缩放。
在进行旋转操作时,我们也将图形的中心点移动到Canvas的原点,按照原点旋转指定度数,当图形在原点旋转成功后,再进行一次平移,将图形移动到原位置,就完成了图形在Canvas中的旋转。
(一)多图组合变换前的准备。根据以上分析我们可以得出结论,一个图形的呈现形式取决于它的坐标、大小和旋转角度。坐标是指相对于容器左上角的远近,大小就是图形本身的宽和高,旋转角度是图形有没有转动,这些因素确定后整个图形的显示效果也就确定了。
那么对于多个图形呈现在一个容器中,并且打算对多个图形同时做变换操作,这一多图组合的变换也会受坐标、大小和旋转角度影响。为了能够准确的计算出多图组合的变换,必须提前计算出组合内每个图形的坐标(为了计算方便使用中心点取代)、大小和旋转角度。
同时需要计算出组合后的大图形的中心点、大小和旋转角度。假定每次组合时,组合后的图形旋转角度为0,表示没有做过任何旋转。而组合后图形的中心点取决于所有单个图形组成大图形的外边界构成图形的中心。如图4所示。

图4 两个图形组合后的图形
假设图形2的中心点x坐标和y坐标都比图形1的中心点x坐标和y坐标大,则有:
组合图形的中心点x坐标=(图形2的中心点x坐标+图形2的宽度)/2+图形1的中心点x坐标-图形1的宽度/2
组合图形的中心点y坐标=(图形2的中心点y坐标+图形2的高度)/2+图形1的中心点y坐标-图形1的高度/2
组合图形的宽度=图形2的中心点x坐标+图形2的宽度
组合图形的高度=图形2的中心点y坐标+图形2的高度
其中图形2的中心点x坐标代表了两个图形中心点x坐标中的最大者,图形2的中心点y坐标代表了两个图形中心点y坐标中的最大者。因此,即使是多个图形也可以按此原则求出最大x坐标和最大y坐标。再用该x坐标加上对应宽度的一半就是该组合后图形的宽度,用该y坐标加上对应高度的一半就是该组合图形的高度。
(二)多图组合变换的实现。
1.多图组合的平移。对于组合图形的平移变换,与每个图形的平移变换并没有两样,所谓组合图形的平移变换也就是对每一个小图形逐个进行平移。具体来说就是获取每个小图形的TransformGroup实例,对其中的TranslateTransform进行操作,平移每个小图形的结果就是对组合图形的平移。
2.多图组合的缩放。组合图形的缩放比例与组合内的每个小图形缩放比例仍然是一致的。首先计算出组合图形的中心点平移至Canvas原点平移量,再将每个小图形平移至相对新中心点的位置,然后再计算出每个小图形平移至Canvas原点的平移量,将每个小图形平移至Canvas原点,再按缩放比例对每个小图形进行缩放。当缩放完毕后,按刚才一系列平移的相反次序再进行平移至相对原始中心点的位置。至此完成多图组合的缩放。如图5所示。

图5 多图组合的缩放
3.多图组合的旋转。先计算出组合图形的中心点平移至Canvas原点的平移量,再将每个小图形平移至相对新中心点的位置,然后再将每个小图形再次平移至Canvas的原点位置进行旋转,每个小图形的旋转角度与整个组合后的大图形旋转角度保持一致,所不同的是每个小图形的平移量是不同的。当每个小图形的旋转完毕后,再按之前平移的相反次序进行平移,平移至相对原始中心点的位置。至此完成多图组合的旋转。如图6所示。

图6 多图组合的旋转
五、结语
计算机图形变换是图形处理中非常重要的环节。利用矩阵理论能够非常好的解决图形中所有点的变换问题。本文通过使用WPF中提供的图形变换类以及相关辅助类实现了单一图形的变换操作。重点分析研究了多图组合时图形变换的问题,并提供了相应的解决方案,该解决方案较好的实现了多图组合的图形变换操作。
[1][美]DONALD HEARN.计算机图形学:第3版[M].蔡士杰译,北京:电子工业出版社,2005:188.
[2]王汝传.计算机图形学教程[M].北京:人民邮电出版社, 2009:126.
[3]张雁.制图学[M].北京:高等教育出版社,1955:208-224.
[4]JanP.Norbye.发动机设计与制图[M].华盛顿:奇尔顿图书出版社,1971:102-105.
[5]MarthaLAbellJamesP.Braselton.Mathematica的举例应用[M].纽约:埃森威尔图书出版社,2004:103-110.
[6]刘极峰.计算机辅助设计与制造[M].北京:高等教育出版社,201l:5-150.
[责任编辑 郑丽娟]
TP311
A
2095-0438(2017)06-0142-04
2017-03-02
侯海平(1980-),男,安徽无为人,安徽财贸职业学院讲师,硕士,研究方向:软件工程、管理信息化。
安徽省高等学校省级质量工程教学研究重点项目(编号:2015jyxm629);安徽省高等学校省级质量工程教学研究重点项目(编号:2016jyxm0032)
