埃博拉病毒病的传播模型及其防控仿真
2017-06-15宋贽,陶桂洪,张阚
宋 贽, 陶 桂 洪, 张 阚
( 沈阳农业大学 理学院, 辽宁 沈阳 110866 )
埃博拉病毒病的传播模型及其防控仿真
宋 贽, 陶 桂 洪, 张 阚
( 沈阳农业大学 理学院, 辽宁 沈阳 110866 )
为研究埃博拉病毒病的流行规律和发展趋势,选用世界卫生组织(WHO)发布的利比里亚(Liberia)从2014年5月25日至11月16日的统计数据,分别对控前和控后两个阶段建立SEIR传染病模型,模型中的传染率参数在采取控制措施后发生变化。利用最小二乘法拟合及Matlab软件,模拟传染病流行趋势,拟合最优参数值,并给出仿真图。对干预措施开始时间作敏感度分析,发现累计最大感染人数对其呈指数增长规律,模型预测每延迟1 d开始干预措施,累计最大感染人数会增加200多人。得出基本再生数的公式,控前R0=1.43,控后R1=0.2,说明采取的宣传教育、追踪隔离等控制措施是有效的。
埃博拉病毒病;SEIR传染病模型;基本再生数;参数估计
0 引 言
埃博拉病毒病(Ebola virus disease,EVD),又称埃博拉出血热(Ebola hemorrhagic fever,EHF),该病是由埃博拉病毒(Ebola virus)感染引起的一种烈性传染病,病死率高达50%~90%,是高传染率和致死率的传染病[1-4]。2013年12月,西非地区的几内亚最先开始出现埃博拉病毒病暴发的疫情,随后,利比里亚、塞拉利昂和尼日利亚等西非国家相继爆发埃博拉病毒病。截止至2014年12月17日,WHO发布数据显示,利比里亚、塞拉利昂和几内亚等西非三国的感染病例(包括疑似病例)已达19 031人,其中死亡人数达到7 373人。
国内文献主要从医学角度分析埃博拉病毒病致病机理,研究发病症状、传播途径、潜伏期、致死率、药物和疫苗研发等问题。也有学者结合数学模型进行研究,江华等[5]建立SIR传染病模型,得到了病毒传染人数对启动应急预案时刻呈指数上涨规律,模拟了不同防控策略对该病在我国传播及爆发流行模式的影响。Chowell等[6]使用1995年刚果和2000年乌干达地区爆发的埃博拉病毒病数据,建立SEIR传染病模型,量化了基本再生数对疾病其他相关系数的敏感性。但是这些模型都没有考虑因病死亡率,由于埃博拉病毒病是高致死率的传染病,在模型中加入因病死亡率,更符合实际情况,并且对影响传染病传播的关键参数做了更深入的分析,给出了函数关系。本研究针对埃博拉病毒病在利比里亚地区的传播情况建模,传播规律可分为控前和控后两个阶段,分别建立SEIR模型。
1 模型及求解
1.1 控前模型
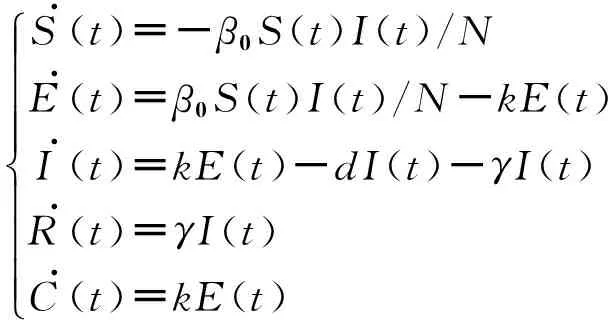
S.(t)=-β0S(t)I(t)/NE.(t)=β0S(t)I(t)/N-kE(t)I.(t)=kE(t)-dI(t)-γI(t)R.(t)=γI(t)C.(t)=kE(t)ìîíïïïïïïï
式中:S(t)为易感者,即未被埃博拉病毒病感染的自由环境中的人员;E(t)为潜伏者,即已被病毒感染,但尚未发病;I(t)为染病者被感染发病,具有较强的传染力;R(t)为治愈者;C(t)不是SEIR传染病模型中的类别,用来累加总的发病人数;N是总人口数,取N=3 476 608。
疾病的平均潜伏期为1/k,由于埃博拉病毒病的平均潜伏期是6.3 d[7],故k=0.15,γ是恢复率系数,埃博拉病毒病的平均病程一般是7 d,从而γ=1/7=0.14。
设δ是染病者的因病死亡率,埃博拉病毒病是高致死率的传染病。由于δ=累计死亡人数/累计病人数,根据WHO给出的累计病人数、累计死亡人数,对δ作最小平方误差估计,拟合出δ=0.715,从而d=0.715/7=0.1。
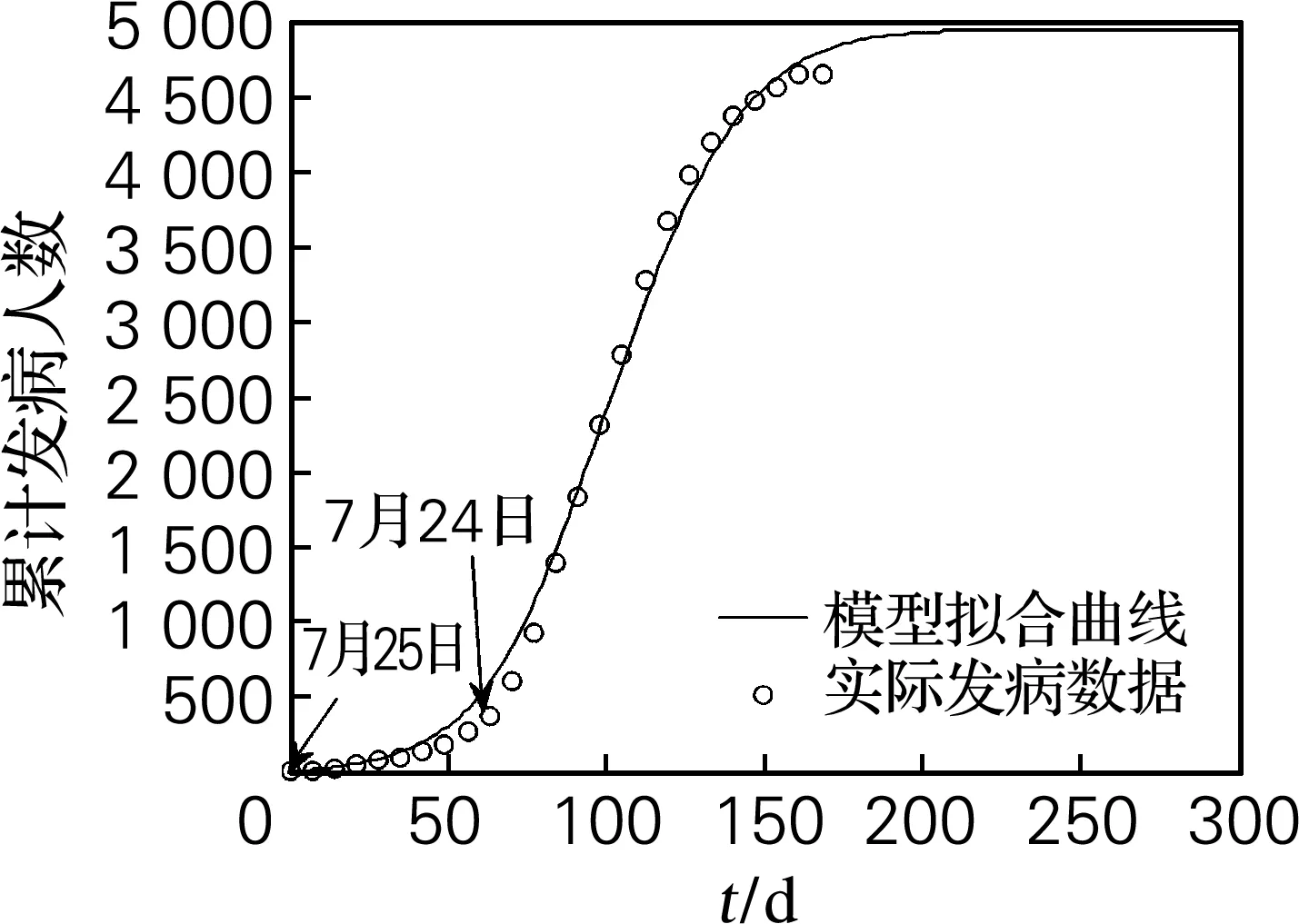
β0是采取控制措施前的传染率系数,反映发病期病毒性的强弱。根据WHO公布的Liberia从5月25日至7月24日的发病数据,利用最小二乘法,通过模型(1)的累计病人数C(t),拟合传染率β0,使用Matlab软件编程[8],选取适合的初值(0<β0<1)。最优化过程重复10次,每次对β0选取两个不同的初值,从而选择最优解,最终拟合的最优解为β0=0.343 2,拟合效果见图1、2。图1中,模型预测曲线总误差为27.54。图2中,模型预测曲线总误差为33.31。
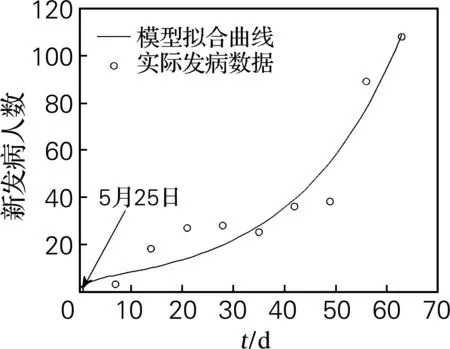
图1 控前每日新发病人数随时间的变化曲线
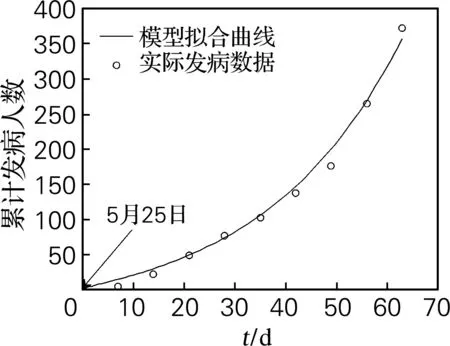
图2 控前累计发病人数随时间的变化曲线
1.2 控后模型
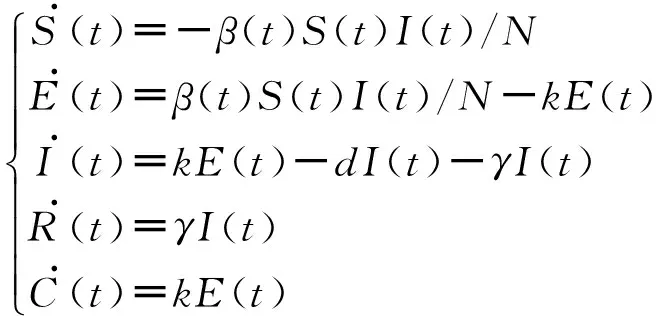
S.(t)=-β(t)S(t)I(t)/NE.(t)=β(t)S(t)I(t)/N-kE(t)I.(t)=kE(t)-dI(t)-γI(t)R.(t)=γI(t)C.(t)=kE(t)ìîíïïïïïïï
式中:k=0.15,d=0.1,γ=0.14,β0=0.343 2;β(t) 为采取控制措施后的传染率系数。但是,干预措施不是及时生效的,有一定的延迟,从开始执行干预措施到生效的过程中,传染率系数是逐渐从β0下降到β1,可以用式(1)描述:
(1)
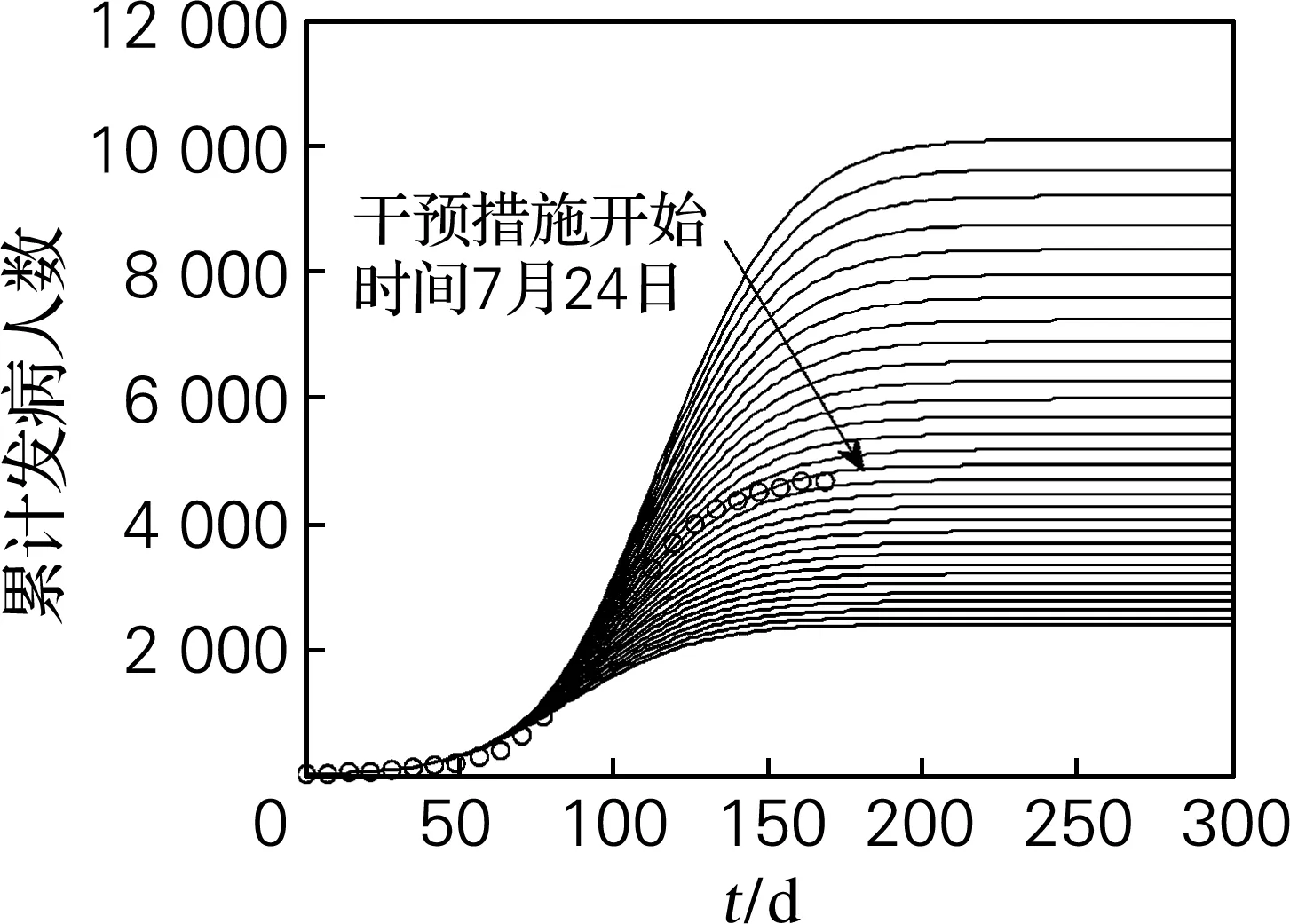
式中:τ为干预措施开始的时间,利比里亚从7月24日开始采取干预措施,因此τ=60 d。q为干预措施的实施强度,反映β(t)变化的快慢。β1和q为待估计的参数,估计方法类似于控前模型的参数估计,利用最小二乘法,通过模型(2)的累计病人数C(t),拟合参数β1和q,使用Matlab软件编程,选取适合的初值(0<β1<β0,0 图3 控后每日新发病人数随时间变化曲线 图4 累计发病人数随时间变化曲线 从图3可以看出,发病高峰期大约在8月中旬到9月底,高峰期每日新发病人数可达500人,高峰期过后发病人数慢慢减少,直到12月底以后疾病会缓慢消亡。从图4可以看出,11月中下旬以后趋于平稳,累计发病人数最高达5 000人。 在其他参数保持不变的前提下,对干预措施开始时间作灵敏度分析,令干预措施的开始时间从提前15 d到延后15 d,即τ∈[45,75],分别观察它对累计最大感染人数的影响,结果如图5、图6所示。 图5 累计发病人数对干预开始时间敏感度分析 图6 最终累计病人数对干预措施开始时间的敏感度分析 Fig.6 Sensitivity of the final epidemic size to the start time of interventions E. , I. 线性化,得到相应的雅可比矩阵为 其特征方程为 λ2+(k+d+γ)λ+(d+γ-β)k=0 参数的定义和最优拟合值见表1。 表1 模型中参数的定义和最优拟合值 根据表1模型拟合出的参数值可得, 控制前 控制后 说明采取的干预措施对控制埃博拉病毒病流行是有效的,进一步,通过计算可知,在控制措施开始后的51 d,传染率下降为(β0+β1)/2。 在所有对模型有影响的参数中,干预措施开始时间是具有压倒性影响的,由于累计最大感染人数随干预措施开始时间呈指数增长规律,指数方程为y=aebx,其中a=4 932(95%CI(4 929,4 934)),b=0.048 02(95%CI(0.047 97,0.048 07)),模型预测延迟1 d开始隔离等控制措施,就会导致累计最大感染人数增加200多人。这是因为有效的干预措施能够使疾病的传染率下降至一半以下,进一步计算得到,干预措施开始后传染率下降到(β0+β1)/2需要51 d。采取控制措施后,基本再生数也有明显的降低,从R0=1.43(>1) 下降到R1=0.2(<1),从而传染病从流行到逐渐消亡。但是,由于这次埃博拉病毒病出现后,利比里亚政府和公众对疾病的认识不够,采取控制措施较晚,导致采取干预措施后51 d疾病的传染率才下降到(β0+β1)/2=0.196 6,对应Rp=0.819(<1),虽然行动最终逆转了传染病暴发的趋势,不过在形势转好前先恶化。 此外,通过模拟发现,干预措施的实施强度和初始染病人数对于累计最大感染人数没有显著的影响。 [1] BAIZE S. Ebola virus in West Africa: new conquered territories and new risks-or how I learned to stop worrying and (not) love Ebola virus[J]. Current Opinion in Virology, 2015, 10: 70-76. [2] CAMACHO A, KUCHARSKI A J, FUNK S, et al. Potential for large outbreaks of Ebola virus disease[J]. Epidemics, 2014, 9: 70-78. [3] 程颖,刘军,李昱,等.埃博拉病毒病:病原学、致病机制、治疗与疫苗研究进展[J].科学通报,2014,59(30):2889-2899. [4] 张应涛,刘康康,陆家海.2014年西非埃博拉出血热流行状况与防控研究[J].暨南大学学报(自然科学与医学版),2014,35(5):421-426. [5] 江华,潘海霞,孙明伟,等.基于计算流行病学的埃博拉出血热的传播与爆发仿真研究[J].中华急诊医学杂志,2014,23(9):974-978. [6] CHOWELL G, HENGARTNER N W, CASTILLO-CHAVEZ C, et al. The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda[J]. Journal of Theoretical Biology, 2004, 229(1): 119-126. [7] MERLER S, AJELLI M, FUMANELLI L, et al. Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: a computational modelling analysis[J]. Lancet Infectious Diseases, 2015, 15(2): 204-211. [8] 薛定宇,陈阳泉.控制数学问题的MATLAB求解[M].北京:清华大学出版社,2007. [9] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004. Modeling and simulation of prevention and control of the spread of the Ebola virus disease SONG Zhi, TAO Guihong, ZHANG Kan ( College of Science, Shenyang Agricultural University, Shenyang 110866, China ) The course of the outbreaks had been modeled via anSEIRepidemic model to study the transmission rule and trends of Ebola virus disease including a smooth transition in the transmission rate after control interventions, of which data were collected from May 25 to Nov. 16, 2014. The result showed that the model parameters were fitted to the Liberia Ebola outbreak data by least-squares fit, the ‘best fit’ parameters and simulation charts had been obtained using Matlab. The sensitivity of the final epidemic size to the time interventions begin (τ) had been analysed, numerical solutions showed that the final epidemic size grew exponentially fast withτand it is predicted that there were 200 more cases if interventions started one day later. A formula for the basic reproductive numberR0has been given, the significant reduction from the basic reproductive number (R0=1.43) to the post-intervention replacement number (R1=0.2) in the estimates for Liberia showed that the implementation of control measures such as education, contact tracing and quarantine would have a significant effect on lowering the effective reproductive rate of Ebola virus disease. Ebola virus disease;SEIRepidemic model; basic reproductive number; parameter estimation 2016-05-19. 辽宁省教育科学规划课题(JG16DB389);中华农业科教基金教材建设研究项目(NKJ201503031);辽宁省教育厅科学研究项目(LSNYB201609). 宋 贽(1982-),女,讲师;通信作者:陶桂洪(1980-),男,讲师,E-mail:guihong_tao@sina.com. O175 A 1674-1404(2017)03-0223-04 宋贽,陶桂洪,张阚.埃博拉病毒病的传播模型及其防控仿真[J].大连工业大学学报,2017,36(3):223-226. SONG Zhi, TAO Guihong, ZHANG Kan. Modeling and simulation of prevention and control of the spread of the Ebola virus disease[J]. Journal of Dalian Polytechnic University, 2017, 36(3): 223-226.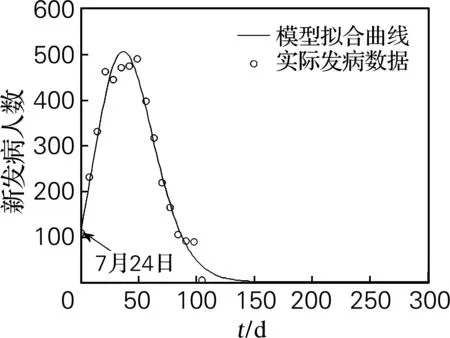
2 干预措施开始时间对埃博拉病毒病流行趋势的影响

3 基本再生数

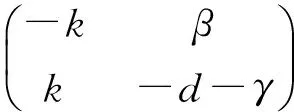





4 结 论
