基于静态电压稳定性和可再生能源消纳最大化的微电网规划

廉静如，张鸽

(山西农业大学 软件学院， 山西 太谷 030801)

基于静态电压稳定性和可再生能源消纳最大化的微电网规划

廉静如，张鸽*

(山西农业大学 软件学院， 山西 太谷 030801)

[目的]微电网中分布式电源(distribution generation，简称DG)接入位置及容量直接影响了微电网静态电压的稳定性，进而影响着可再生能源消纳问题。为了建立可再生能源消纳最大、微电网静态电压稳定、含环境效益的DG投资成本最小的微电网规划模型。[方法]采用离差法将多目标优化问题转化为单目标规划问题，利用粒子群算法求解多目标函数的最优解，利用MATLAB软件搭建典型的微电网算例系统，并进行了测试。[结果]得到了在微电网静态电压稳定性基础上，可再生能源消纳最大化的微电网的规划方案。[结论]该方案既能满足微电网建设的可靠性和经济性要求，又能解决可再生能源消纳问题。

微电网； 电压稳定； 多目标优化； 可再生能源消纳； 微电网规划

由于风能、太阳能等可再生能源的随机性、间歇性[1～4]，导致很难控制其自身的有功出力，制约着可再生能源利用和发展。解决这一问题的一个有效途径是将分布式电源接入微电网。微电网中分布式电源的安装容量和位置会影响可再生能源的并网进程。目前，微电网研究主要集中在微电源建模、运行和控制等方面，并且缺乏相关成熟的理论。因此，研究计及微电网静态稳定和最大化消纳可再生能源的微电网规划方法十分重要，可有效推动风电和光伏发电的并网进程。

国内外一些学者从分布式电源安装等的费用、微电网的可靠性和安全性、以及分布式电源节能环保角度对微电网规划设计问题进行了研究，并取得了一定的成果。陈建[5]等的研究考虑了不同控制策略下，以分布式电源的各种成本为最优化目标的微电网优化配置问题；洪博文[6]等研究了以经济和环境成本最小为目标，建立微电网优化调度模型。上述文献都只考虑了微电网的经济性问题，优化目标较为单一。杨琦[7]等提出了微电网规划评价指标包含可靠性、经济性、环保性和商业运行。确保微电网中DG安装成本最经济、微电网可靠性最强、环境保护最佳、带来最大经济效益。上述优化目标在整个微电网规划中所占比重可能存在不同，甚至相互矛盾。刘梦璇[8]等建立了包含海水淡化负荷的独立微电网多目标优化模型，但负荷较为局限，模型也较为理想化。谭兴国[9]等建立了装置成本最低、功率匹配最佳、可再生能源输出功率平滑最好的3目标优化模型，但其研究重点是储能而非整个微电网。邱晓燕[10]等建立了DG有功出力最大、投资费用最小、网损最小的多目标优化模型，来确定系统DG的容量和位置，但其研究对象是智能电网而非微电网。

本文从可靠性、经济性和环保性等方面建立分布式电源规划的多目标模型，其中目标函数由可再生能源消纳、微电网静态电压稳定性和考虑环境效益的DG投资成本3个因子组成。采用离差排序法将上述3个量纲不同的子目标转换成单目标规划，然后用粒子群算法求解出最优解，并利用MATLAB软件进行仿真，构建典型微电网仿真算例，验证所提规划方案的有效性，从而建立可再生能源消纳最大化的微电网规划设计方案。

1 微电网规划的多目标优化模型

本文采用的典型微电网算例[11]如图1所示，包含了风力发电系统、光伏发电系统、蓄电池、燃料电池等多种分布式电源。其中，光伏阵列、风电机组、蓄电池等通过逆变器接入交流母线上。接入微电网的系统负荷分为不可控负荷、可转移负荷和可中断负荷。本文将从可再生能源消纳最大化、微电网静态电压稳定性、计及环境效益的DG投资成本等方面建立多目标优化模型。

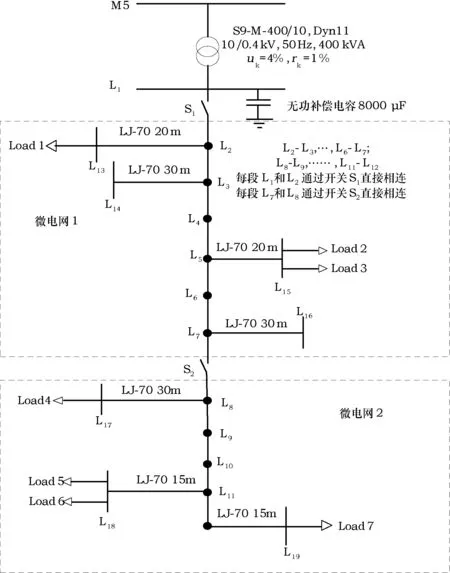
图1 典型微电网算例系统Fig.1 Example system of low voltage micro-grid

1.1 可再生能源消纳最大

在当前能源需求及电力发展的双重压力下，可再生能源发电成为电力发展的新方向，同时，其消纳最大化也成为微电网优化配置的一个关键目标。因此，该目标函数为：

(1)

式中：λi为第i个DG 的功率因数；m为接入的DG总个数；SDGi为第i个DG的容量， kVA。

1.2 静态电压稳定裕度最大

一般情况下，分布式电源(DG)的接入会减小微电网系统中支路潮流的流动，但当其渗透率较高时，反而会增加支路潮流流动。因此，DG接入微电网的位置和容量不同，会影响微电网潮流的分布。本文基于潮流解存在性[12]的方法对微电网静态电压稳定指标进行量化，如式(2)。

(2)

式中：Lij为任意条支路bij(i为首端节点，j为末端节点)的静态电压稳定指标；Pj和Qj分别为节点j处支路输出的有功功率和无功功率；Rij、Xij分别为支路的电阻和电抗；Ui为首端电压幅值。

对于整个微电网，电压稳定指标L定义为所有支路电压稳定指标的最大值，如式(3)。

(3)

Lij最大的支路即为系统电压稳定性最薄弱的支路，与L对应。微电网的静态电压稳定性要求当微电网处于静态电压稳定时，L值小于1.0。当微电网系统发生静态电压崩溃时，系统一定是从L值最大(即最薄弱)支路开始的。因此，可以将L的值与临界值1.0的距离定义为电压稳定裕度，来判断系统电压稳定的程度。静态电压稳定裕度最大的目标函数f2等价为：

minf2=minL

(4)

1.3 DG投资成本最小

可再生能源发电技术日益受到重视的一个主要原因是绝大多数可再生能源发电系统具有环境友好性。因此，在计算分布式发电成本时，除了考虑可见资金外，还须考虑环境效益。考虑环境成本的分布式发电成本为[13]：

COM,i+Cf+Ce]

(5)

式中，αi为第i种分布式发电方式占总平均输出能量的比例系数；ni为投资偿还期，一般规定其等于设备的使用年限；Caz,i为安装成本；COM,i为运行和维护成本；r为固定年利率；Cf为单位电量需要燃烧燃料的成本，当不需要购买使用燃料时，此项为零；Ce为发电的环境成本，其表达式为：

(6)

式中，NP表示污染物种类数量；Mei为第i种污染物的环境价值标准，元/kg；Hi表示第i种污染物的排放量，kg；Mi为排放每单位第i种污染物所受罚款，元。

DG投资成本使用的目标函数f3：

(7)

式中，Ch考虑环境成本的分布式发电成本，元；nDG为可安装DG的节点总数；Prati为安装在第i个节点的DG额定容量，KVA。

1.4 约束条件

约束条件包括等式约束和不等式约束。本文选取的等式约束为功率平衡约束。不等式约束包括节点电压上下限制和支路功率最大限制。如下式表示：

(8)

式中，V为节点电压幅值。Pl为支路有功功率向量，PPV,i为光伏发电输出功率，PW,i为风力发电输出功率，Puc,i为储能系统输出功率，PL,i为负荷消耗功率。

1.5 多目标函数处理

采用线性加权的方法，聚合多目标函数为单目标函数。根据式(9)，同时结合各单目标的重要程度，将单目标函数值分别与权系数λi相乘，然后相加获得最终的单目标函数

(9)

根据离差排序方法确定权系数λi(i=1,2,3)。离差表示系统接入不同容量的DG时，目标函数的值与最优值之间的差距。它的表达式为：

(10)

式中：m为目标的个数，此处为3；fij=fi(xj)，为DG取不同容量和位置时目标函数的值。

离差排序算法步骤为：

(1)设系统共有m个单目标，分别求出以各单目标最优情况下的最优解minfi(x) (i=1,2,…,m)，记作xi。

(2)将各单目标函数最优情况下得到的解代入其他目标函数，并且计算相应的目标函数值fij。

(3)根据公式(10)，计算每个最优解xi时，其他目标函数的离差δij。

(4)求解每个目标的平均离差：

(11)

因为δii=0，所以分母取m-1求取平均离差。

(5)计算各权系数：

(12)

2 求解方法

采用粒子群算法来求解多目标优化问题。粒子按式(13)更新自身位置xid和速度vid。

(13)

式中，c1和c2为学习因子，也称加速常数(acceleration constant)，根据文献[14]，取c1=2.8，c2=1.3。Pid为自身最优位置，ggd为全局最优位置；r1和r2为[0，1]范围内的均匀随机数；w是保持原来速度的系数，取0.4。

3 算例分析

本文采用典型的低压微电网算例系统，系统电压等级为400 V，主馈线L2～L3，L3～L4，……，L6～L7，L8～L9，……，L11～L12，均为长度50 m的LJ_95型导线。L2～L13，L3～L14，L5～L15，L7～L16，L8～L17，L11～L18，L12～L19均采用LJ_70型导线，具体参数见图1，导线参数见表1。微电网中DG的类型、额定有功功率及功率因数等配置见表2，DG的安装节点集合为{L14，L16，L17，L18，L19}。各节点电压电压幅值的标幺Vmin取0.94，Vmax取1.06。粒子群的个数为500，迭代次数为100。

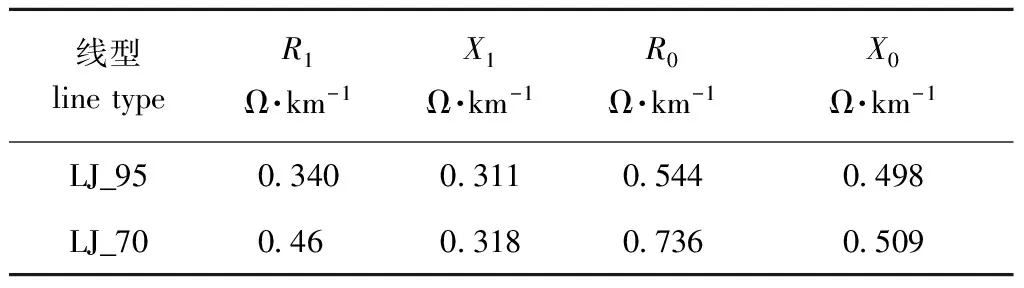
表1 低压微电网算例导线参数

表2 分布式电源配置参数

表3为单目标和多目标优化配置的结果。其中，方案1、方案2、方案3分别对应可再生能源消纳、微电网静态电压稳定、含环境效益的DG投资成本指标的3个子目标优化结果。方案4为以上3个单目标结合的多目标优化结果。

对比表3中的4个方案，在不同补偿目标下，对分布式容量的要求差异较大。方案1中可再生能源消纳容量最大，但是很大程度上牺牲了静态电压稳定性和投资成本；方案2静态电压稳定性最好，但是没有达到可再生能源消纳最大化的要求，经济性也较差；方案3投资成本最低，只满足经济性要求，但是可再生能源消纳最大化的目标没有考虑，并且牺牲了静态电压稳定性。而方案4中可再生能源消纳容量不是最大，静态电压稳定性不是最好，投资成本也不是最低，但方案4兼顾了上述3种情况，即能达到可再生能源消纳最大化目的，又能在微电网静态电压稳定的前提下考虑了经济性。

从表4分析可知，分布式电源优化配置前，系统节点电压水平总体上偏低，而且有多个节点电压越限，系统运行状态不合理。优化配置分布式电源后，系统的电压偏移问题很大程度上得到了改善，且系统节点电压分布情况比较合理。可见，DG的合理配置能有效改善微电网系统的电压水平。

表3 单目标和多目标优化结果

注：规划结果一栏中，括号外数字表示优化后安装DG的母线号，括号内数字表示优化后DG的安装容量

Note: In the planning results, the parenthese indicate the line number of DG installed after optinization, and the installed capacitg in parentheses

表4 分布式电源优化配置前后系统端电压

Table 4 The system voltage which before and after the optimization configuration of distributed generation

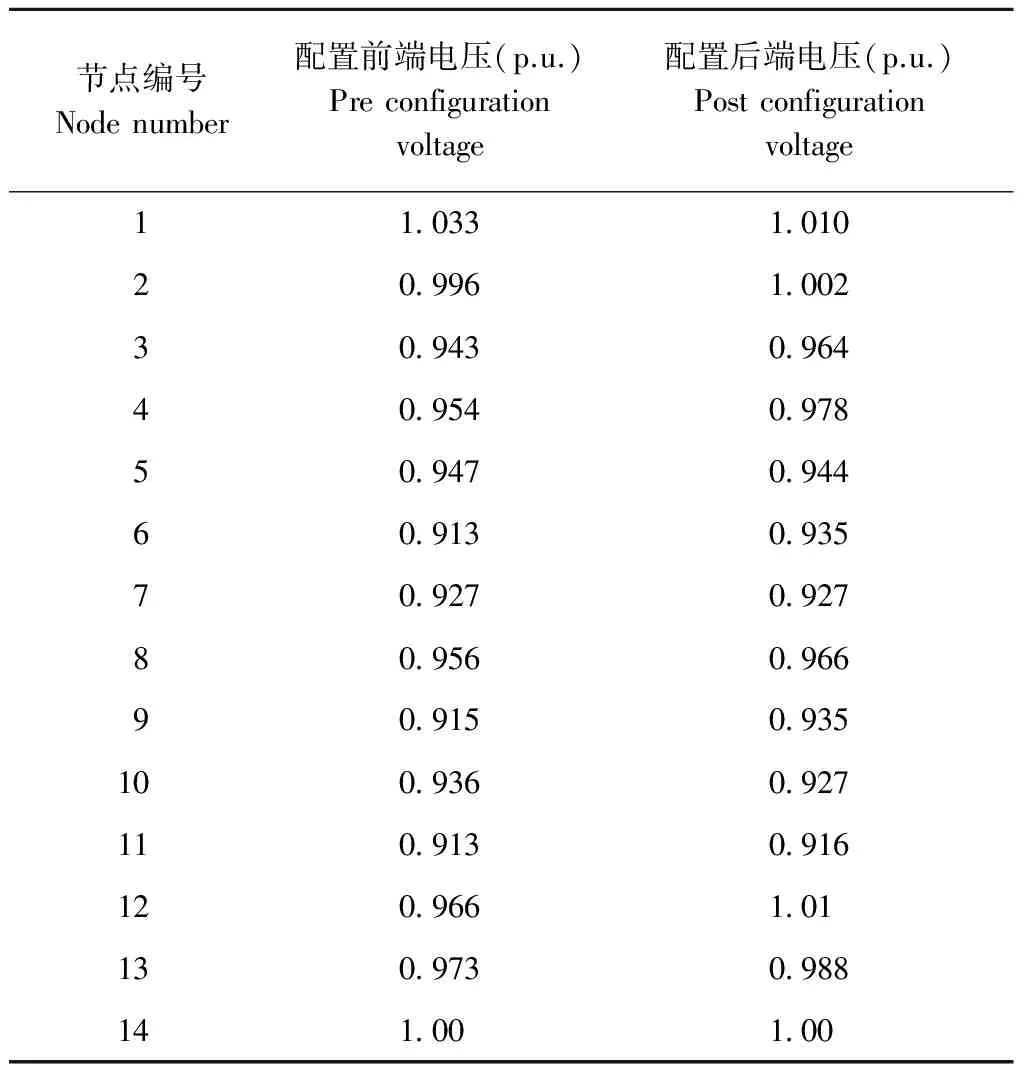
节点编号Nodenumber配置前端电压(p．u．)Preconfigurationvoltage配置后端电压(p．u．)Postconfigurationvoltage11033101020996100230943096440954097850947094460913093570927092780956096690915093510093609271109130916120966101130973098814100100

综合单目标和多目标优化的结果分析，考虑微电网的经济性、可靠性及环保性，建立的可再生能源消纳最大、微电网静态电压稳定、含环境效益的DG投资成本最低的多目标规划方案能够合理的协调不同目标之间的关系，达到设计者对微电网规划的在静态电压稳定的前提下可再生能源消纳最大化的要求。并且，合理的规划微电网中分布式电源的安装位置和容量，能有效改善微电网电压水平。

4 结论

本文基于典型微电网算例系统，考虑微电网的经济性、可靠性及环保性，建立了可再生能源消纳最大、微电网静态电压稳定、含环境效益的DG投资成本最低的多目标优化设计模型，利用粒子群算法求得的最优方案4中，可再生能源的利用率提高到0.08066MW，静态电压稳定裕度为0.644，满足稳定性要求，投资成本为1.02元/Kwh，经济性较好；并且对比规划前后，该方案能有效改善电压偏移问题。。表明文中所建立的DG规划模型能够有效协调不同目标之间的关系，可以在微电网静态电压稳定的前提下，使得微电网中可再生能源消纳最大化，并且获得经济上的平衡，达到设计者对可再生能源消纳最大化的要求。

[1]王成山，郑海峰，谢莹华，等.计及分布式发电的配电系统随机潮流计算[J].电力系统自动化,2005,29(24):39-44

[2]张美霞，陈洁，杨秀，等.考虑风光和负荷随机性的微网三相潮流计算[J].中国电机工程学报,2013,33(13):101-107

[3]丁明，王京景，李生虎.基于扩展拉丁超立方采样的电力系统概率潮流计算[J].中国电机工程学报,2013,33(4):163-170.

[4]杨三根，陈峦，曹瓅月，等.基于风速Weibull分布的电力系统备用容量优化模型[J].可再生能源,2013,31(10):49-52

[5]陈建，王成山，赵波，等.考虑不同控制策略的独立型微电网优化配置[J].电力系统自动化,2013,37(11):1-6.

[6]洪博文，郭力，王成山，等.微电网多目标动态优化调度模型与方法[J].电力自动化设备,2013,33(3):100-107.

[7]杨琦，马世英，唐晓骏，等.微电网规划评价指标体系构建与应用[J].电力系统自动化,2012,36(9):13-17.

[8]刘梦璇，王成山，郭力，等.基于多目标的独立微电网优化设计方法[J].电力系统自动化,2012,36(17):34-39.

[9]谭兴国，王辉，张黎，等.微电网复合储能多目标优化配置方法及评价指标[J].电力系统自动化,2014,38(8):7-14.

[10]邱晓燕，夏莉丽，李兴源.智能电网建设中分布式电源的规划[J].电网技术,2010,34(4):7-10.

[11]彭克，王成山.典型中低压微电网算例系统设计[J].电力系统自动化,2011,35(18):31-35.

[12]武晓朦，刘健，毕鹏翔．配电网电压稳定性研究[J]．电网技术，2006，30(24)：31-35.

[13]崔弘.考虑环境效益的分布式电源优化配置研究[D].华南理工大学，2010.

[14]Carisle A,Dozier G.An off-the-shelf POS[C].Proceedings of the Workshop on Particle Swarm Optimization,Indianapolis,IN,2001:1-6.

(编辑：李晓斌)

Planning for micro-grid with static voltage stability and maximizing renewable energy consumption

Lian Jingru, Zhang Ge*

(Collegeofsoftware,ShanxiAgriculturalUniversity,Taigu030801,China)

[Objective] The access position and capacity of distribution generation (DG) in micro-grid directly affect the static voltage stability，thus affecting the renewable energy utilization problem. A multi-objective optimization model was established, this model had three advantages, which were the largest renewable energy utilization, static voltage stability of micro-grid and the minimum cost of DG investment considering environmental benefits. [Methods] In this paper, the multi-objective optimization problem was transformed into a single objective programming problem using the deviation method; the optimal solution of multi-objective function was solved by using particle swarm optimization algorithm, so as to establish the planning scheme of micro-grid. A typical example system of micro-grid was built and tested using MATLAB. [Results]Obtained a planning scheme of micro-grid with the largest renewable energy utilization on the basis of the static voltage stability.[Conclusion]The scheme can not only satisfy the economy and reliability of micro-grid but can also solve the renewable energy utilization problem.

Micro-grid， Voltage stability， Multiple-objective planning， Particle swarm optimization， Planning for micro-grid

2016-11-02

2017-02-11

廉静如(1989-)，女(汉)，山西临汾人，助教，硕士，研究方向：微电网算法、可再生能源

*通信作者：张鸽，助教。Tel:15835055086；E-mail: 1055809995@qq.com

山西农业大学科技创新基金(2016003)

O221.6

A

1671-8151(2017)05-0371-06