数形结合解题误区分析
2017-06-15河北省唐山市第一中学姚洪琪
河北省唐山市第一中学 姚洪琪
数形结合解题误区分析
河北省唐山市第一中学 姚洪琪
数学本来就是研究数量及图形的特征、规律及其关系的一门学科,那么应用数形结合的方法解决数学问题就成了一种重要的解题方法,著名数学家华罗庚的一首诗对此有过精彩的描述:“数缺形时少直观,形少数时难入微,数形结合百般好,割裂分家万事休。”但是从教学实践看,学生在应用中仍然存在一些误区,下面对这一问题做一些分析。
一、缺乏数形结合的解题意识
有些学生在解决数学问题时只看到题目的表象,缺乏数与形之间的联想,不能适时选择最合适的解题方法,影响了解题的速度和正确率。
A.f(x)在区间[-2π,0]上是减函数
B.f(x)在区间[-3π,-π]上是增函数
C.f(x)在区间[3π,5π]上是减函数
D.f(x)在区间[4π,6π]上是增函数

【分析】学生在解决该问题时,一般都是想办法从已知条件中求出ω和φ,再利用正弦函数的单调区间即可得出答案,费时较多,错误率也较高。如果考虑到由条件时取得最大值及最小正周期为6π,即可得到函数f(x)上递增,所以在[-2π,0]上递增,答案A错误,在[-3π,-π]和[3π,5π]上不单调,故答案B、C错误,而在[4π,6π]上递增,从而选择答案D。
例2已知m、n是正整数,且1≤m<n,则有()

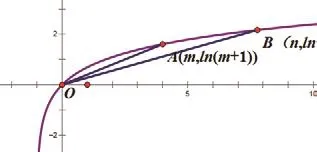
二、认为只有函数图象才能应用数形结合解题
数形结合体现的是数量与图形的结合,不一定必须是与函数图象有关的问题,像集合、向量、三角函数、解析几何、数列、线性规划等,都可以利用数形结合的方法解决。

【分析】本题最容易想到的是将M点的坐标代入直线方程,再用三角函数的方法解决,但如果注意到点M在单位圆上,则转化为直线与圆有公共点,即相交或相切问题,也就是原点到直线的距离小于或等于半径1,从而可轻松得到答案D。
例4[2013新课标I卷]设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,…。若b1>c1,b1+c1=
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n-1}为递增数列,{S2n}为递减数列
D.{S2n-1}为递减数列,{S2n}为递增数列
三、画图不准,判断失误
应用数形结合方法解题,最容易出现的失误就是所画出的图象不准确,尤其是在一些关键部位不能做出图形走向的准确判断导致错误解题,此时必须要辅助代数计算进行准确的探究,真正体现“数”与“形”的结合。
例5已知函数f(x)在(-1,3]上的解析式为:

A.2个B.3个C.4个D.1个

A.(2,+∞)B.(-∞,-2)C.(1,+∞)D.(-∞,-1)
总之,数形结合是一种重要的解题方法,不但要在解题实践中注意培养数形结合的意识,更要注意通过“数”与“形”的结合作出准确的图形判断。只有做到“感性观察”与“理性分析”的有机结合,才能正确解题。
book=68,ebook=70
