基于复合多尺度熵与拉普拉斯支持向量机的滚动轴承故障诊断方法

代俊习 郑近德 潘海洋 潘紫微

安徽工业大学机械工程学院，马鞍山，243032



基于复合多尺度熵与拉普拉斯支持向量机的滚动轴承故障诊断方法

代俊习 郑近德 潘海洋 潘紫微

安徽工业大学机械工程学院，马鞍山，243032

针对早期滚动故障特征不明显和特征提取难等问题，将一种新的衡量时间序列复杂性的方法——复合多尺度熵(CMSE)应用于滚动轴承故障振动信号的特征提取。CMSE克服了多尺度熵中粗粒化方式的不足，得到的熵值一致性和稳定性好。同时，针对机械故障智能诊断中收集大量的样本比较容易而要对所有的样本进行类别标记却较为困难这一问题，将拉普拉斯支持向量机(LapSVM)应用于滚动轴承故障的智能诊断中。在此基础上，提出了一种基于CMSE，序列前向选择(SFS)特征选择和LapSVM的滚动轴承故障诊断方法。最后，将提出的方法应用于试验数据分析，结果表明：CMSE能够有效地提取滚动轴承的故障特征；当有标记样本的数量较少时，与仅使用有标记样本进行学习的支持向量机相比，结合SFS特征选择的LapSVM方法利用大量的无标记样本进行辅助学习，可以显著提高故障诊断的正确率。

多尺度熵；复合多尺度熵；支持向量机；拉普拉斯支持向量机；故障诊断

0 引言

航空发动机、汽轮机、压缩机和风机等旋转机械在国防、能源、电力、冶金和化工等领域发挥着重要的作用,因此，对此类旋转机械故障诊断的技术和方法进行研究具有重要的理论和实际意义[1]。文献[2-3]分别研究了转子和滚动轴承故障信号的分形特征。文献[4]将分形与近似熵进行了对比研究，结果表明，近似熵包含更多的信息，故障特征区分更明显和客观。文献[5]将近似熵作为一种机械设备运行状态的监测工具，能够准确地反映早期故障的发生与变化。但是，近似熵存在自身模态的匹配问题，为此，文献[6]提出了改进的近似熵——样本熵(sample entropy，SampEn)。在此基础上，文献[7]提出了基于经验模态分解与样本熵的滚动轴承故障诊断方法。事实上，样本熵和近似熵都是单一尺度的分析方法，并不能完全反映时间序列的复杂性特征。为了克服样本熵的缺陷，文献[8]发展了多尺度熵(multiscale entropy，MSE)的概念。文献[9-10]将多尺度熵应用于滚动轴承和转子系统故障诊断，结果表明多尺度熵能够有效地区别各种故障。与传统的基于单一尺度的样本熵相比，MSE能够更好地从多个尺度反映时间序列的复杂性特征，而且具有计算所需数据短、稳定性好、抗噪能力强等优点，已经被广泛应用于生物、肌电、脑电和机械故障等信号的分析中[11-13]。但在MSE粗粒化序列的计算中，由于尺度因子增大而使得序列长度变短，从而导致MSE在尺度较大时稳定性和一致性较差，出现端点“飞翼”现象。为此，文献[14]提出了复合多尺度熵(composite multiscale entropy，CMSE)的概念。CMSE通过对同一尺度下的不同时间序列的样本熵值进行平均，得到的信息更为准确和客观。

在提取到故障特征之后，为了实现滚动轴承的故障智能诊断和分类，需要选择合适的模式识别方法，拉普拉斯支持向量机[15](Laplacian support vector machines, LapSVM)是一种将流形学习思想和支持向量机相结合的半监督学习方法，半监督学习[16]方法可以利用少量的标记样本和大量的无标记样本进行学习，它将无标记样本的内在流形结构信息融入到分类器的设计中，相较于仅用有标记样本进行学习分类，其正确率明显提高。文献[17]将其应用于旋转机械故障诊断，取得了良好的诊断效果。

本文将CMSE和LapSVM方法应用于滚动轴承故障诊断。同时，为了避免由故障特征维数过高带来的训练耗时和信息冗余等问题，将序列前向选择(sequential forward selection，SFS)特征选择方法引入到机械故障特征的选择和降维中。将本文提出的这种基于CMSE、SFS和LapSVM的滚动轴承故障诊断方法应用于滚动轴承试验数据分析，分析结果表明了该方法的有效性。

1 复合多尺度熵理论

1.1 多尺度熵

多尺度熵(MSE)的计算是在样本熵的基础上，将原始数据进行粗粒化并将各个尺度上的样本熵值组成一组数列，即时间序列在不同尺度下的样本熵。如果一个序列和另一个序列在同种尺度下，前者的熵值比后者高，这说明前者的时间序列的复杂性要高于后者。MSE计算步骤如下。

(1)设原始数据为Xi={x1,x2,…,xN}，长度为N，建立粗粒化序列

(1)

其中,τ是正整数，称为尺度因子。事实上，yj(1)即为原时间序列。对于非零τ，Xi被分割成τ个长度为[N/τ]([·]表示不大于N/τ的正整数)的粗粒化序列{yj(τ)}。

(2)在相同的相似容限下，计算τ个粗粒序列的样本熵[18]，并转化成尺度因子τ的函数。

式(1)定义的粗粒化序列依赖于时间序列的长度，由于每个粗粒化序列的长度等于原时间序列的长度除以尺度因子，因此尺度因子越大，粗粒化序列的长度越短，熵值的偏差会随着粗粒化序列长度减小而逐渐增大，估计误差也会随着尺度因子的增大而增大。为了避免信息遗漏，文献[17]通过复合粗粒化的方式提出了复合多尺度熵(CMSE)的概念。

1.2 复合多尺度熵

复合多尺度熵是为了克服MSE中粗粒化方式的不足，即遗漏了部分尺度信息而提出来的，它的计算步骤如下：

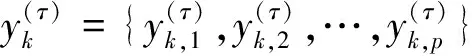
(2)

j=1,2,…,N/τk=1,2,…,τ

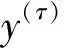
(3)

将得到的熵值转化成尺度因子的函数，这个过程称为复合多尺度熵分析。

CMSE综合考虑了尺度因子为τ时的所有τ个粗粒化序列的信息，克服了MSE只考虑单一的粗粒化序列的缺陷，避免了由于粗粒化时间序列时间长度减小而引起的熵值波动。因此，与MSE曲线相比，随着尺度因子的增大，CMSE曲线的变化更加平滑。

1.3 CMSE与MSE对比分析

为了说明CMSE的意义及优越性，不失一般地，首先取长度分别为1500、2000、2500、3000、3500和4000的高斯白噪声和1/f(f指f倍频)噪声作为研究对象。分别计算二者的MSE和CMSE，结果如图1所示，其中嵌入的维数m=2，相似容限r=0.15σ(σ为原始数据的标准差)，最大尺度因子取20。由图1可以看出，当N≤2000时，高斯白噪声和1/f噪声的MSE结果与其他长度的MSE有一定的误差，而N>2000时，高斯白噪声和1/f噪声的MSE结果与其他长度的MSE误差很小，这说明，当长度大于2000时，时间序列的长度对CMSE的影响非常小;因此，一般地，当最大尺度因子小于或等于20时，时间序列的长度取2000。此外，从相同长度的两种信号的MSE和CMSE也可以看出，CMSE的变化趋势随尺度因子的增大其变化较均匀，与CMSE相比，MSE曲线随着尺度因子的增大有轻微的波动，且在曲线右端波动增大，这说明CMSE更具有稳定性和优越性。最后，从两种信号的MSE和CMSE变化趋势来看，高斯白噪声信号的CMSE和MSE曲线随着尺度因子的增大而逐渐递减，这说明高斯白噪声信号较为简单，只在较低的尺度包含信息。1/f噪声的CMSE和MSE曲线随着尺度因子的增大而变化缓慢，基本稳定在一个恒定值附近，这说明1/f噪声较白噪声信号复杂，不仅在较低的尺度包含信息，而且在其他尺度也包含有重要信息，这个结论与我们关于白噪声和1/f噪声信号的定义和认识相符。

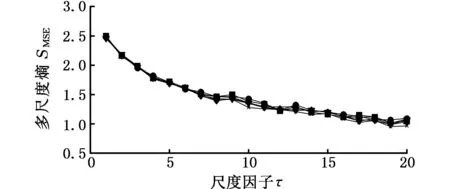
(a)不同长度白噪声的MSE

(b)不同长度白噪声的CMSE

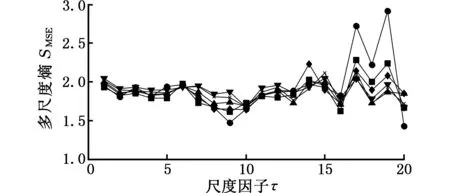
(c)不同长度1/f噪声的MSE

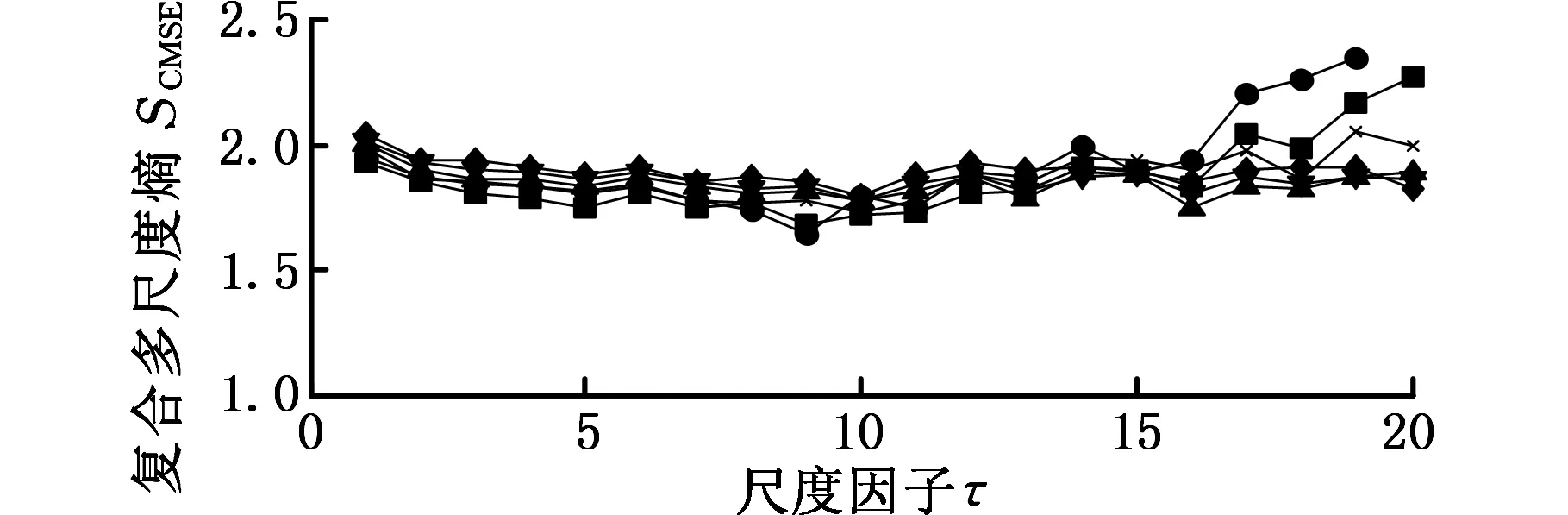
(d)不同长度1/f噪声的CMSE

图1 时间序列长度对熵值的影响Fig.1 The influence of data length on entropy values

为了研究相似容限r对CMSE结果的影响，以相同长度的高斯白噪声和1/f噪声作为研究对象。对不同的r=0.05σ、0.1σ、0.15σ、0.2σ，分别计算二者的MSE和CMSE，结果如图2所示，其中m=2时，最大尺度因子取20。r表示模糊函数边界的宽度，由图2可以看出，相似容限对MSE和CMSE的计算结果影响较大，r越大，匹配的模板越少，熵值越小，r越小，匹配的模板越多，熵值越大。r过大会丢失掉很多统计信息；r过小估计出的统计特性效果不理想，而且会增加对结果噪声的敏感性。一般r取(0.1～0.25)σ，本文取r=0.15σ。

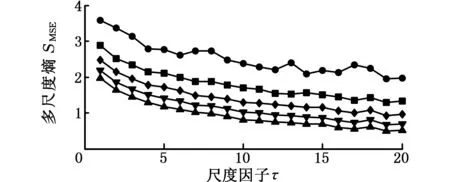
(a)不同相似容限r条件下白噪声的MSE

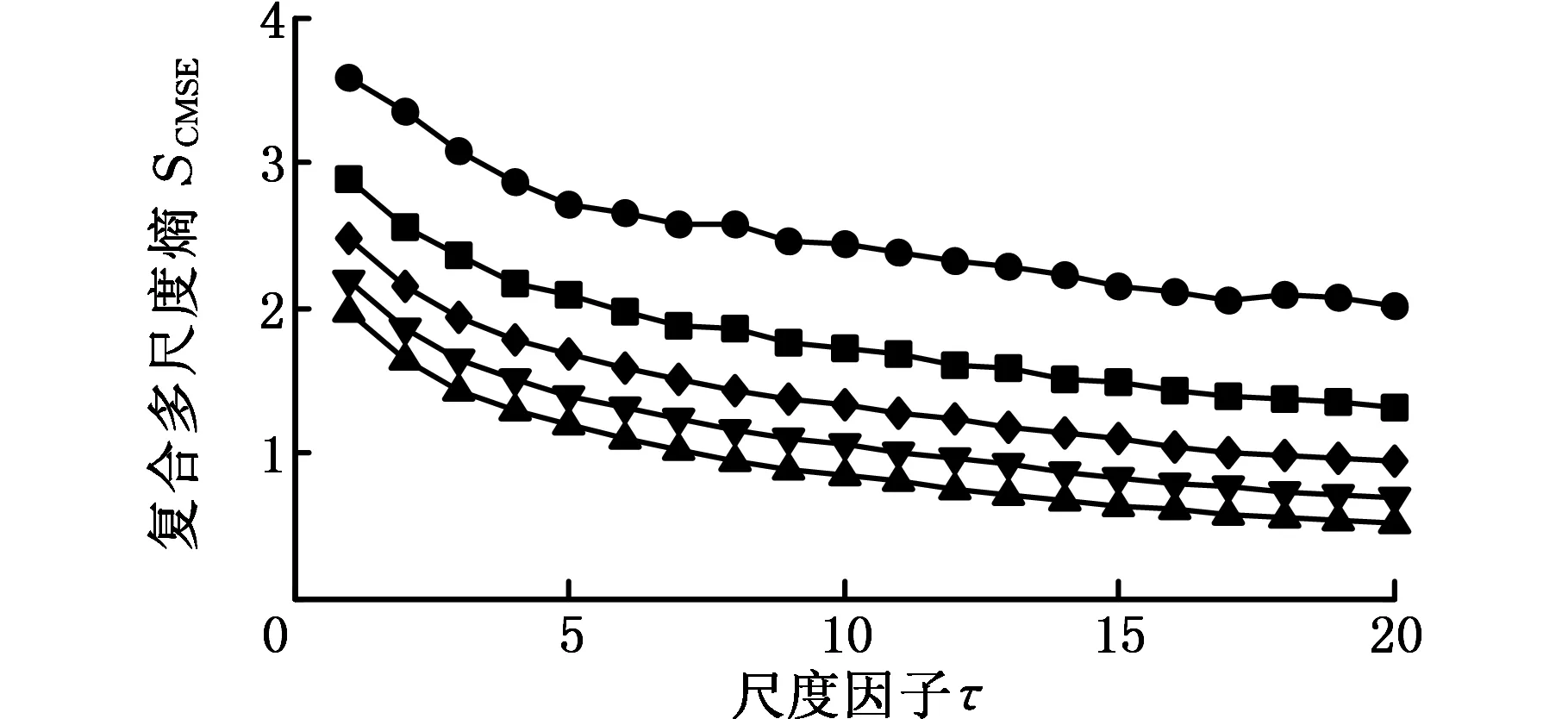
(b)不同相似容限r条件下白噪声的CMSE

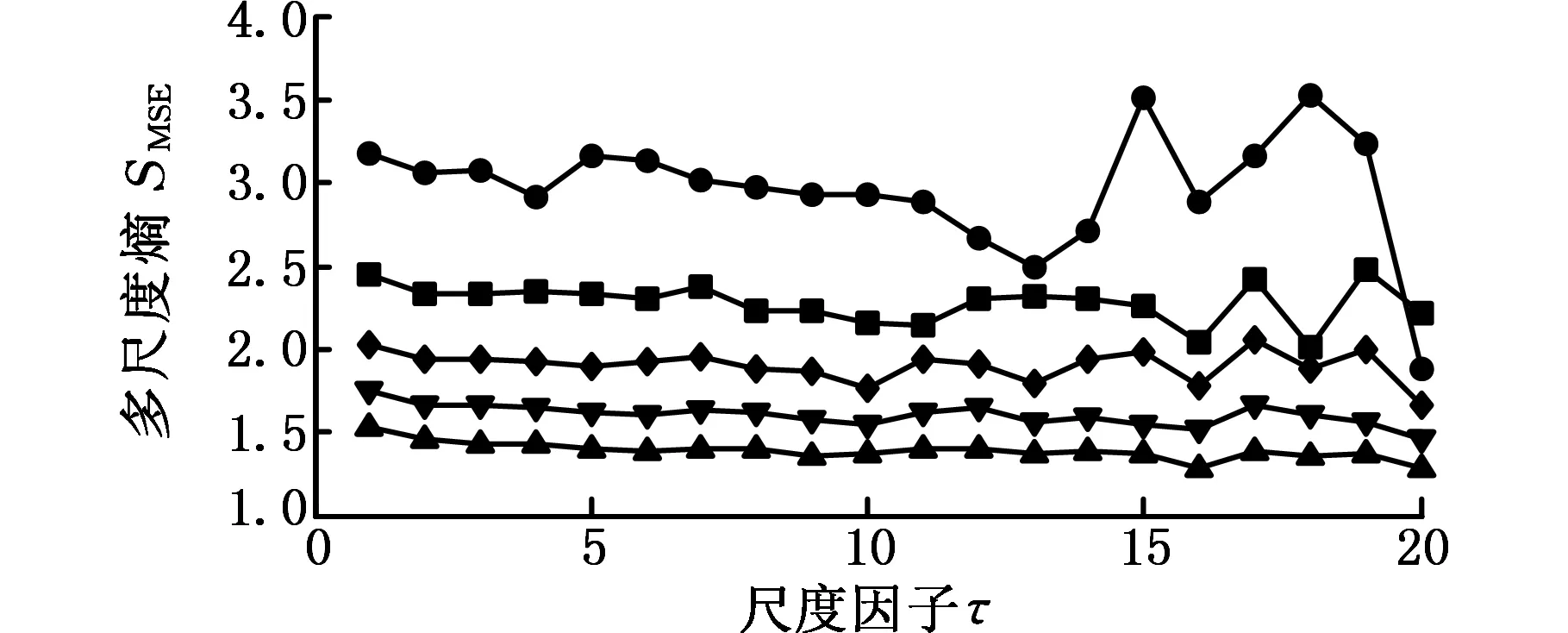
(c)不同相似容限r条件下1/f噪声的MSE

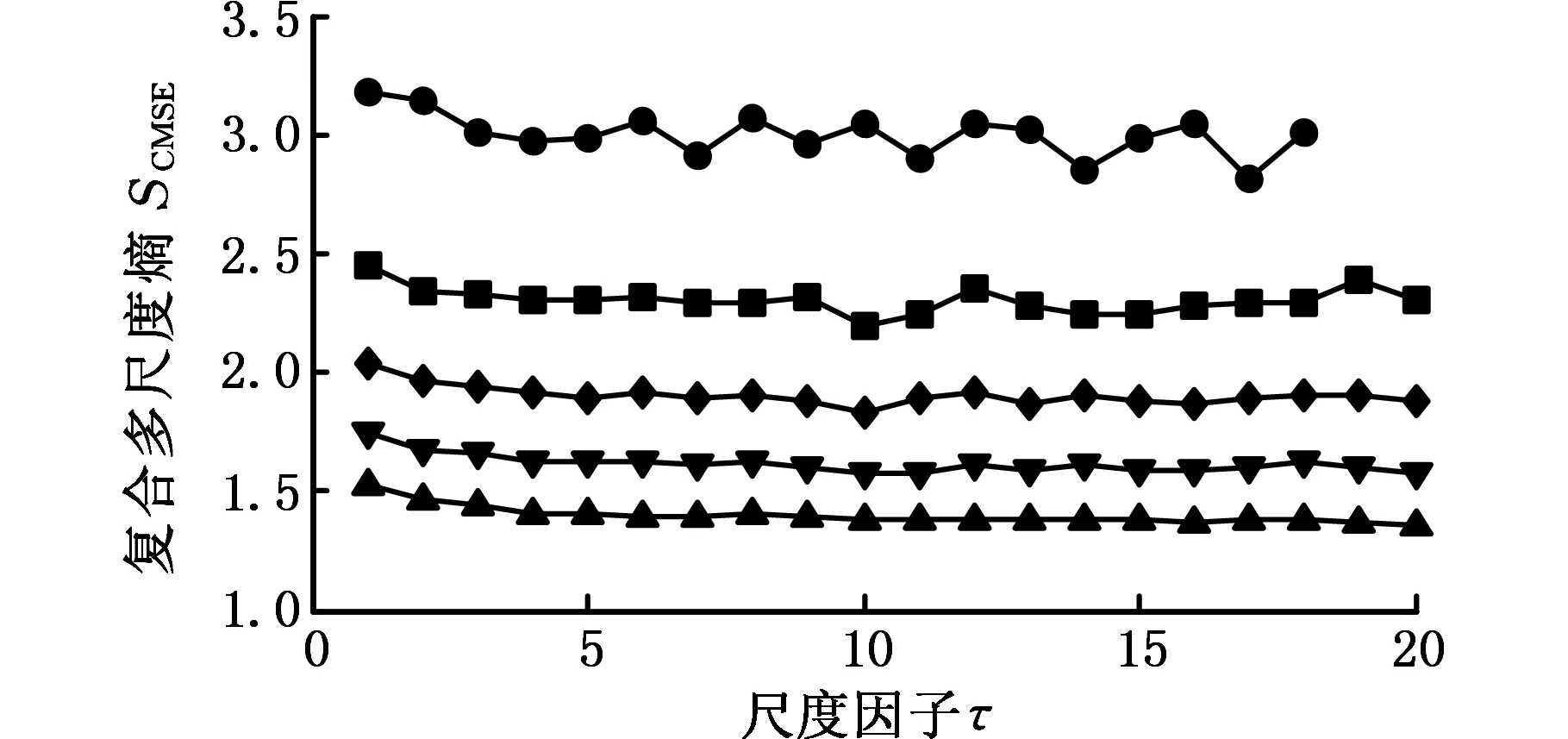
(d)不同相似容限r条件下1/f噪声的CMSE

图2 相似容限对熵值的影响Fig.2 The influence of r on entropy values

2 拉普拉斯支持向量机方法

拉普拉斯支持向量机是一种可以有效地利用少量有标记样本和大量无标记样本来辅助提高分类性能的模式无监督学习方法。LapSVM是流形正则化的一个实例，而流形正则化的基本思想是在一个外围的子流形上分布着数据，利用大量无标记的数据估计出内在的数据流形结构，然后将流形结构信息融入到分类器的设计之中，流形正则化是在传统正则化算法框架基础上提出的一个半监督学习框架。当给定一组有标记的样本(xi,yi)(i=1,2,…,l)以及核函数K时，传统正则化算法的框架可以表示为

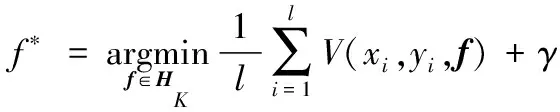
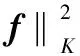
则流形正则化的框架可以表示为[15]

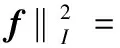
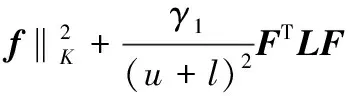
(4)

F=[f(x1)f(x2) …f(xl+u)]T

(5)

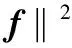
当将损失函数取为铰链损失函数时，即令

V(xi,yi,f)=(1-yif(xi))+=

max(0,1-yif(xi)),yi∈{-1,1}

将其代入式(4)，得到：

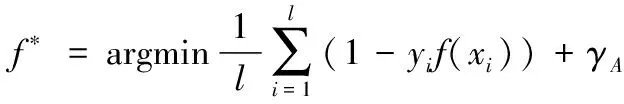
(6)

由表示定理[15]得到式(6)的解为

(7)

(8)

Y=diag(y1,y2,…,yl)

式中，I为(l+u)×(l+u)的单位矩阵；L为(l+u)×(l+u)的拉普拉斯矩阵；K为(l+u)×(l+u)的核矩阵；J为l×(l+u)的矩阵。

β*可以通过二次问题规划得到:

(9)

令

(10)

0≤βi≤1/l

则

(11)

3 基于CMSE、SFS与LapSVM的滚动轴承故障诊断方法

3.1 方法步骤

基于上述分析，本文将LapSVM应用于滚动轴承故障诊断中。为了避免故障特征维数过高带来的训练耗时和信息冗余等问题，采用序列前向选择(SFS)特征选择方法对得到的故障特征进行选择和降维。在此基础上，笔者提出一种基于CMSE、SFS与LapSVM的滚动轴承故障诊断方法。具体步骤如下：

本文方法流程如图3所示。

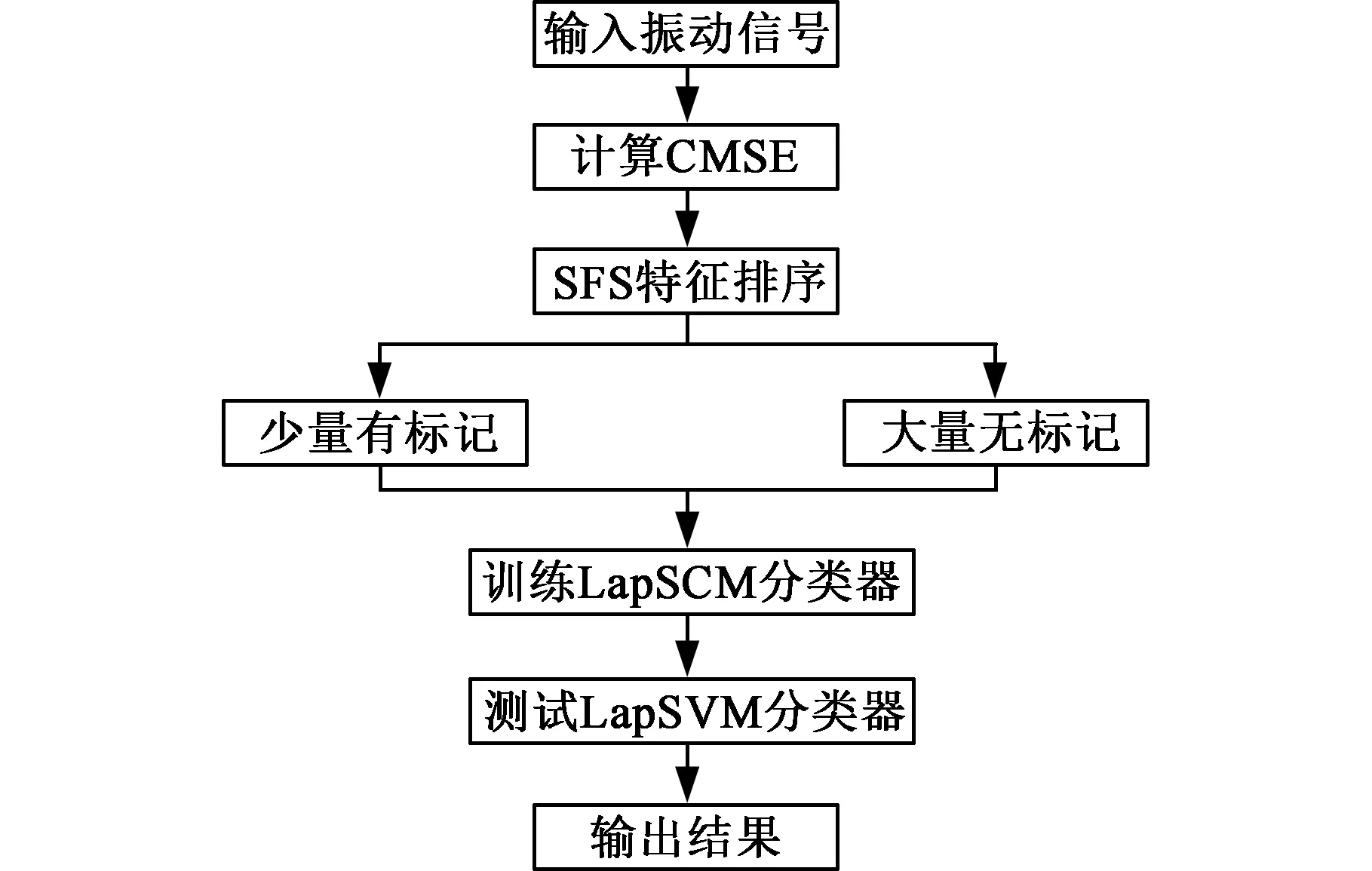
图3 本文方法流程图Fig.3 The paper method flow chart

3.2 试验数据分析

为了说明方法的有效性，将所提出的方法应用于试验数据分析。试验数据来自美国Case Western Reserve University的滚动轴承数据中心[19]。测试轴承为6205-2RSJEM SK F深沟球轴承，使用电火花加工技术在轴承上布置单点故障，故障直径为0.053 34 mm，深度为0.2794 mm，转速为1797 r/min，采样频率为12 kHz。采集到具有局部单点电蚀的内圈(inner race, IR)、外圈(outer race，OR)、滚动体故障(ball element, BE)和正常(norm)四种状态的振动信号，它们的时域波形如图4所示。

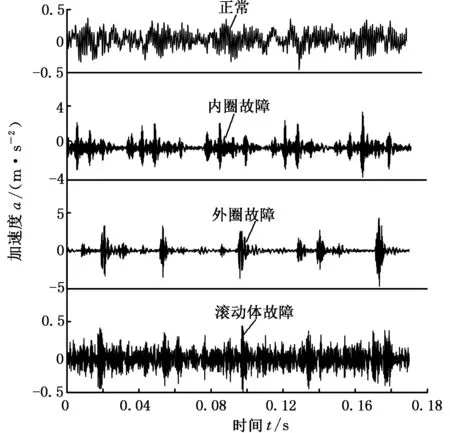
图4 滚动轴承振动信号的时域波形Fig.4 Time domain waveforms of vibration signal of rolling bearings

将本文提出的故障诊断方法应用于上述试验数据分析。具体步骤如下：

(1)取正常、内圈故障、外圈故障和滚动体故障四种状态的试验数据，每种状态取58个样本，共得到232个样本。计算所有样本的CMSE，得到它们的特征集{Tk,K},Tk∈Rmk×τmax，τmax=20，mk=58,k=1,2,3,4。

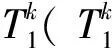
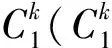
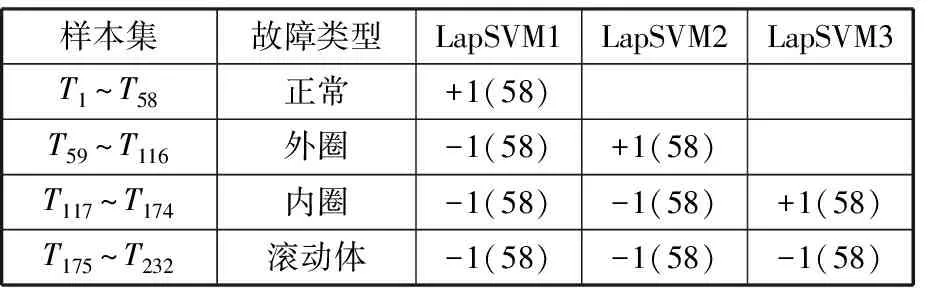
表1 本文方法测试样本诊断结果

从表1可以看出，本文提出的滚动轴承故障诊断方法有很高的识别效率，对试验数据的识别率达到100%。

为了说明标记样本个数对识别结果的影响，当分别采用5、10、15个样本进行标记，并选用前3～10个最佳特征值作为敏感故障特征子集时，识别率如表2所示。由表2可知，当特征值个数为3时，随着标记样本个数的增加，识别率逐渐升高；而当特征值个数大于等于4时，标记样本个数对识别率的影响较小。

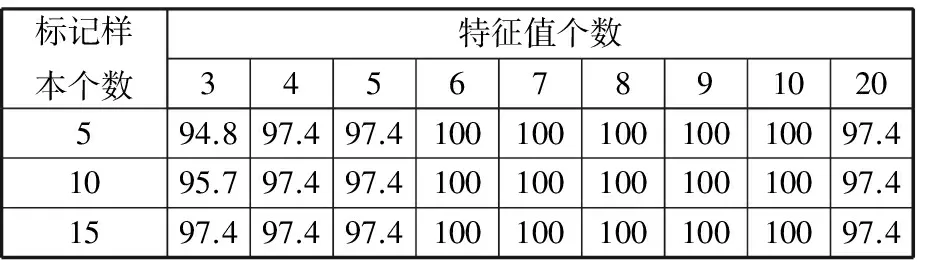
表2 LapSVM诊断故障总正确率

为了说明LapSVM相对于SVM的优越性，将SVM与LapSVM进行对比分析，其中SVM采用LibSVM程序[20]。SVM和LapSVM的核函数均选取高斯径向基函数。支持向量机惩罚参数c和核函数参数g进行优化选择，并采用粒子群优化算法对参数进行优化[21]。当训练样本个数为5、10、15时，选用前3～10、15、20个最佳特征值作为敏感故障特征子集进行训练。相应的测试样本SVM故障分类器识别率如表3所示。由表3可以看出，当选择相同的敏感故障特征时，LapSVM的识别率要比SVM的识别率高；SVM的识别率受训练样本个数的影响较大。

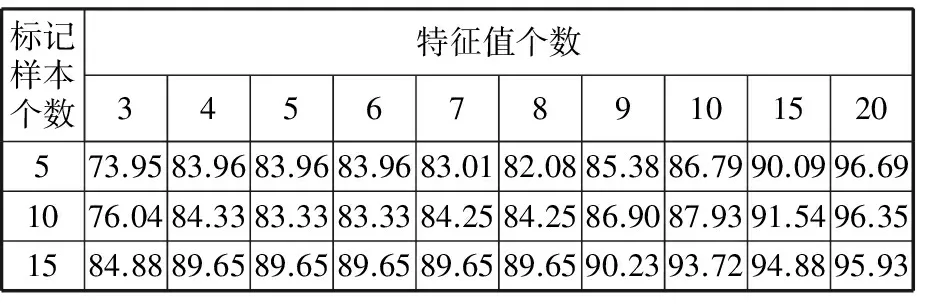
表3 基于SFS的SVM识别率

为了说明SFS进行特征选择的必要性，首先采用全部的CMSE值(τmax=20)作为特征向量，不进行特征选择。采用LapSVM分类器对故障特征进行训练和识别，结果如表2所示。由表2可以看出，当采用全部特征值作为敏感故障特征时，识别率均是97.4%，识别率要低于本文方法进行SFS特征选择的识别率(100%)。这是因为，一般情况下特征之间存在相关性和冗余性，往往几个关键性的特征而非全部特征引导着对象之间的差别[22-23]。依据这些特征就可以表述各个状态之间的差别，如果可以直接选出这些导致区别的关键特征，就可以直接或间接找到解决各个状态之间差异的方法，而不需要选择全部特征值表征对象之间的差异。此外，从表2可以看出，随着特征选择个数的增多，当特征值个数大于等于6个时(一般为6～10)，故障识别率达到了100%；而当选用3～5个特征时，随着有标记样本的增多，识别率在逐渐增大，但识别率最高为97.4%，这说明特征值个数较少时，并不能反映故障的全部信息。同时考虑到故障个数越多训练越耗时，因此，一般地，我们选择特征值个数为6个。其次，再考虑随机选择6个特征3、7、9、10、11、19时，与上述相同参数下分别对基于LapSVM的多故障分类器进行训练和测试。结果如表4所示，其中，Ti表示第i(i=1，2，…，232)个样本。从表4可以看出，测试样本的第四类滚动体故障的6个测试样本被错分为第三类内圈故障中，故障识别率为91.67%,因此，随机选择6个特征作为特征向量进行训练和测试的识别率比本文提出方法的识别率要低。上述对比结果说明了采用本文方法进行SFS特征选择的必要性。

表4 随机选择特征时测试样本的诊断结果

事实上，SVM与LapSVM在处理小样本故障识别时有很好的实用性，由表2和表3可以看出,无论训练样本多还是少，LapSVM和SVM都是适用的，随着训练样本的增多，诊断的识别率大体上在明显地提高；表2和表3相比较可以看出，LapSVM的诊断识别率是高于SVM的诊断识别率的，比如选用10个训练样本，5个SFS特征时，支持向量机的诊断识别率是83.33%，而LapSVM的诊断识别率是97.4%。可以看出大量的无标记样本对分类还是产生了很大的影响。

4 结论

(1)通过仿真信号分析将CMSE与MSE进行了对比，结果表明，与MSE相比，随尺度因子的增大，CMSE曲线的变化趋势更加平缓，克服了MSE右端“飞翼”的现象，具有一定的优越性；同时本文研究了数据长度和相似容限的选择对CMSE的影响，研究表明，CMSE在尺度因子较大时受数据长度的变化影响更小，只需较短的数据便可得到稳定的熵值。

(2)将CMSE应用于滚动轴承故障的特征提取，并将其与适合处理标记样本少而无标记样本多的半监督分类方法——拉普拉斯支持向量机(LapSVM)相结合，同时采用序列前向特征选择对特征值进行排序降维，在此基础上提出了一种新的滚动轴承故障诊断方法。将其应用于试验数据分析，结果表明，本文提出的滚动轴承故障诊断方法有很高的故障识别率。

(3)将提出的滚动轴承故障诊断方法与现有方法进行了对比，结果验证了进行SFS特征选择的必要性以及LapSVM相较于SVM的优越性。

[1] 何正嘉，陈进，王太勇，等. 机械故障诊断理论及应用 [M]. 北京:高等教育出版社,2010. HE Zhengjia, CHEN Jin, WANG Taiyong, et al. Theory and Application of Mechanical Fault Diagnosis[M]. Beijing:Higher Education Press,2010.

[2] 程军圣，于德介，杨宇. 基于EMD和分形维数的转子系统故障诊断 [J]. 中国机械工程，2005, 16(12): 1088-1091. CHENG Junsheng, YU Dejie, YANG Yu. Fault Diagnosis for Rotor System Based on EMD and Fractal Dimension [J].China Mechanical Engineering,2005,16(12):1088-1091.

[3] 吕志民，徐金梧. 分形维数及其在滚动轴承故障的诊断中的应用 [J]. 机械工程学报, 1999, 35(2): 88-91. LYU Zhimin, XU Jinwu. Fractal Dimension and Its Application in Fault Diagnosis of Rolling Bearing[J]. Chinese Journal of Mechanical Engineering,1999,35(2):88-91.

[4] 胥永刚，何正嘉.分形维数和近似熵用于度量信号复杂性的比较研究[J].振动与冲击，2003，22(3)：25-27. XU Yonggang, HE Zhengjia. Research on Comparison between Approximate Entropy and Fractal Dimension for Complexity Measure of Signals[J]. Journal of Vibration and Shock,2003,22(3):25-27.

[5] YAN R, GAO R X. Approximate Entropy as a Diagnostic Tool for Machine Health Monitoring[J]. Mechanical Systems and Signal Processing,2007,21(2):824-839.

[6] RICHMAN J S, MOORMAN J R. Physiological Time-series Analysis Using Approximate Entropy and Sample Entropy[J]. American Journal of Physiology-heart and Circulatory Physiology,2000,278(6):H2039-H2049.

[7] 来凌红，吴虎胜，吕建新，等.基于EMD和样本熵的滚动轴承故障SVM识别[J].煤矿机械，2011，32(1)：249-252. LAI Linghong, WU Husheng, LYU Jianxin, et al. SVM Recognition Method Based on EMD and Sample Entropy in Rolling Bearing Fault Diagnosis [J]. Coal Mine Machinery,2011,32(1):249-252.

[8] COSTA M, GOLDBERGER A L, PENG C K. Multiscale Entropy Analysis of Complex Physiologic Time Series[J]. Physical Review Letters,2002,89(6):068102.

[9] 张龙，张磊，熊国良，等. 基于多尺度熵的滚动轴承Elman神经网络故障诊断方法[J]. 机械科学与技术，2014,238(12):1854-1858. ZHANG Long, ZHANG Lei, XIONG Guoliang, et al. Rolling Bearing Fault Diagnosis Based on Multiscale Entropy and Elman Neural Network [J]. Mechanical Science and Technology for Aerospace Engineering,2014,238(12):1854-1858.

[10] 郑近德，程军圣，胡思宇. 多尺度熵在转子故障诊断中的应用[J]. 振动、测试与诊断，2013, 33(2): 294-297. ZHENG Jinde, CHENG Junsheng, HU Siyu. Application of Multiscale Entropy in Rotor Fault Diagnosis [J]. Journal of Vibration Measurement & Diagnosis,2013,33(2):294-297.

[11] COSTA M, GOLDBERGER A L, PENG C K. Multiscale Entropy Analysis of Biological Signals[J]. Physical Review E,2005,71(2):021906.

[12] COSTA M D, PENG C K, GOLDBERGER A L, et al. Multiscale Entropy Analysis of Human Gait Dynamics[J]. Physica A: Statistical Mechanics and Its Applications,2003,330(1):53-60.

[13] ZHANG L, XIONG G, LIU H, et al. Bearing Fault Diagnosis Using Multi-scale Entropy and Adaptive Neuro-fuzzy Inference[J]. Expert Systems with Applications,2010,37(8):6077-6085.

[14] WU S D, WU C W, LIN S G, et al. Time Series Analysis Using Composite Multiscale Entropy[J]. Entropy,2013,15：1069-1084.

[15] BELKIN M, NIYOGI P,SINDHWANI V. Manifold Regularization: a Geometric Framework for Learning from Labeled and Unlabeled Examples[J]. Journal of Machine Learning Research,2006,7(11):2399-2434.

[16] CHAPELLE O, SCHOLKPF O, ZIEN A. Semi-supervised Learning[M]. Cambridge: MIT Press,2006.

[17] 郝腾飞，陈果. 旋转机械故障的拉普拉斯支持向量机诊断方法[J].中国机械工程，2016,27(1)：73-78. HAO Tengfei, CHEN Guo. Fault Diagnosis of Rotating Machinery Based on Laplacian Support Vector Machines [J]. China Mechanical Engineering,2016,27(1):73-78.

[18] 赵志宏，杨绍普.一种基于样本熵的轴承故障诊断方法[J]. 振动与冲击,2012,31(6)：136-154. ZHAO Zhihong, YANG Shaopu. Sample Entropy-based Roller Bearing Fault Diagnosis Method[J]. Journal of Vibration and Shock,2012,31(6):136-154.

[19] The Case Western Reserve University Bearing Data Center.Bearing Data Center Fault Test Data[EB/OL].(2012-03-01)[2016-07-20].http://www.eecs.cwru.edu/laboratory/bearing/.

[20] CHANG C C, LIN C J. LIBSVM:a Library for Support Vector Machines[EB/OL].[2016-07-20]. http://www.csie.ntu.edu.tw/～cjlin/libsvm.

[21] 邵信光，杨慧中，陈刚. 基于粒子群优化算法的支持向量机参数选择及应用[J]. 控制理论与应用，2006,23(5)：740-748.

SHAO Xinguang, YANG Huizhong, CHEN Gang. Parameters Selection and Application of Support Vector Machines Based on Particle Swarm Optimization Algorithm [J]. Control Theory & Applications,2006,23(5):740-748

[22] DOUGHERTY E R，SHMULEVICH I，BITTNER M L. Genomic Signal Processing：The Salient Issues[J]. EURASIP Journal on Applied Signal Processing，2004，4(1)：146-153.

[23] WHITNEY A W. A Direct Method of Nonparametric Measurement Selection[J]. IEEE Transactions on Computers，1971，100(9)：1100-1103.

(编辑 王艳丽)

Rolling Bearing Fault Diagnosis Method Based on Composite Multiscale Entropy and Laplacian SVM

DAI Junxi ZHENG Jinde PAN Haiyang PAN Ziwei

School of Mechanical Engineering, Anhui University of Technology,Ma’anshan,Anhui,243032

Since the unclear of early fault of rolling bearings and it was difficult to extract the features from the mechanical systems, a new judging time series complexity testing method called composite multiscale entropy (CMSE) was applied to extract the fault features from the vibration signals of rolling bearings. CMSE overcome the defects of coarse-graining in MSE and was an effective method for measuring the complexity of time series with better consistency and stability. Besides, as it was easy to collect a large number of samples, but difficult to label them in mechanical fault intelligent diagnosis, the LapSVM was applied to the intelligent fault diagnosis of rolling bearings. Then a new fault diagnosis method for rolling bearings was proposed based on the CMSE, sequential forward selection and LapSVM. Finally, the experimental data were analyzed based on the proposed method. The results show that the fault features of rolling bearings are extracted effectively by CMSE, compared with SVM that may only be trained by the labeled samples, the LapSVM combining with sequential forward selection for feature selection and studying from a large number of unlabeled samples may significantly improve the accuracy of fault diagnosis for fewer number of labeled samples.

multiscale entropy(MSE); composite multiscale entropy; support vector machine(SVM); Laplacian support vector machine(LapSVM); fault diagnosis

2016-07-25

国家自然科学基金资助项目(51505002);安徽省高校自然科学研究重点资助项目(KJ2015A080);安徽工业大学研究生创新研究基金资助项目(2016061)

TN911.7;TH165.3

10.3969/j.issn.1004-132X.2017.11.014

代俊习，男，1992年生。安徽工业大学机械工程学院硕士研究生。主要研究方向为振动信号处理和机械设备故障诊断。E-mail:1228545659@qq.com。 郑近德(通信作者)，男，1986年生。安徽工业大学机械工程学院副教授、博士。 潘海洋，男，1989年生。安徽工业大学机械工程学院讲师。潘紫微，男，1956年生。安徽工业大学机械工程学院教授。