不同锯齿高度对软弱结构面剪切特性的影响

唐雯钰，林杭, 2



不同锯齿高度对软弱结构面剪切特性的影响

唐雯钰1，林杭1, 2

(1. 中南大学资源与安全工程学院，湖南长沙，410083；2. 中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州，221116)

为分析不同法向应力与锯齿高度情况下软弱结构面的剪切行为，通过数值方法建立不同锯齿高度情况下的结构面计算模型，模拟在不同法向应力情况下的直剪试验，探讨结构面抗剪强度峰值前后的应力应变关系。建立剪胀角与锯齿高度之间的线性关系表达式。研究结果表明：随着锯齿高度增大，峰值抗剪强度对应的位移逐渐增大；应变软化阶段应力下降的速率呈先减小后增大的趋势，当锯齿高度与夹层厚度相同时达到最小值；峰值抗剪强度与残余抗剪强度均随锯齿高度的增大而呈线性增大，当锯齿高度达到一定值后，残余强度不发生变化；当锯齿高度较大如80 mm时，结构面法向应力与抗剪强度之间呈现显著的线性关系，而当锯齿高度较小时，两者之间的关系表现出一定的非线性特征，并且此时对应较小法向应力的剪切强度基本相同；随着法向应力增大，应变软化阶段应力下降的速率不断减小，残余强度与峰值强度的比值呈先增大后减小的趋势，最大值为0.961 4。

锯齿高度；软弱结构面；剪切特性；残余强度

岩体中节理力学性质是岩体稳定性的重要影响因素，国内外很多学者对节理岩体的力学性质进行了研究[1−3]，特别是针对无填充的硬性结构面抗剪强度模型建立节理表面形貌经验模型JRC−JCS[4−5]。岩石结构面中常含有软弱介质夹层，人们对其进行了大量研究，如：葛修润[6]提出针对含软弱夹层节理岩体的非线性分析计算模型；程强等[7]通过实验研究了软弱夹层的蠕变和流变性质；高正夏等[8]通过试验和数值模拟对夹层渗透性进行了研究；许宝田等[9]采用FLAC数值方法对软弱夹层边坡的稳定性和岩体变形特征进行了研究；肖卫国等[10]研究了节理充填度的影响并建立了充填节理增量型应力与位移的本构模型；孙辅庭等[11]通过理论方法建立了充填水泥砂浆节理峰值剪切强度的计算公式并通过实验验证其正确性；胡毅方等[12]运用数值方法分析了夹层厚度及剪切速率对软弱结构面强度特性和变形特性的影响。目前，人们一般针对平直或锯齿结构面展开研究，但对于锯齿高度的影响以及结构面剪切强度峰值后力学行为的研究较少，为此，在考虑岩体应变软化特征情况下，本文作者采用数值计算方法针对不同锯齿高度结构面的剪切行为进行研究。

1 数值计算模型

采用FLAC3D数值计算方法进行研究，该方法能够模拟岩土材料在外荷载作用下的应力和变形响应，特别对于大变形情况能够较好地模拟，并且能动态模拟结构面剪切过程中应力和变形的变化情况。但FLAC3D前期建模较复杂[13−15]，为此，本文拟结合ANSYS建模的便捷性，在ANSYS中建立数值模型，然后导入FLAC3D进行计算。由于软弱结构面剪切过程中有可能发生软弱夹层的剪切破坏、沿软弱夹层与岩石的接触面破坏、锯齿剪断破坏，所以，在ANSYS中划分网格时需要兼顾含软弱夹层节理的破坏模 式[16]，在划分软弱结构面以及其上、下部分网格时更加细密。图1和图2所示为其中1个软弱结构面模型，其长×宽×高为4 m×4 m×4 m，共包括16 829个单元和3 381个节点，软弱夹层与岩体均采用实体单元进行模拟。

图1 数值模拟模型

为分析锯齿高度的影响，在建模过程中分别设置不同的锯齿高度，如图3所示。模型上、下2部分均为岩石材料，中间为厚度80 mm的软弱夹层。由于软弱结构面在剪切过程中往往呈现应变软化特征，因此，采用Mohr-Coulomb应变软化模型描述岩体的应力、应变关系，该模型中岩石和软弱夹层的黏结力、内摩擦角、抗拉强度随塑性应变的变化而变化，它们之间的关系如表1和表2所示。表1中，1为岩石黏结力，为岩石抗拉强度，为岩石内摩擦角。表2中，2为软弱夹层黏结力，为软弱夹层抗拉强度；为软弱夹层内摩擦角。计算所取的岩石力学参数参考室内实验[12, 16−17]以及相关工程和模拟的经验岩体力学参数，并且结合《岩石力学参数手册》[18]，采用表3中岩石以及软弱夹层的参数(表3中，为弹性模量，为泊松比，为内摩擦角，为抗拉强度，为黏结力)。

图3 模型平面图

表1 岩石应变软化参数

表2 软弱夹层应变软化参数

表3 岩石和软弱夹层的材料参数

2 数值计算分析

2.1 锯齿高度对抗剪强度的影响

当正应力为0.5 MPa时，不同锯齿高度的结构面在剪切过程中切应力与剪切位移的关系见图4。从图4可以看出应力−位移曲线可分为4部分，即线弹性阶段、应变软化阶段、过渡阶段和残余应力阶段，如图5所示。从图5可见：在线弹性阶段，节理面上切应力随着剪切位移的增大而呈线性增大，经过短暂塑性屈服后达到峰值强度。图6所示为达到峰值时的切向位移与锯齿高度的关系。从图6可见：随着锯齿高度增大，峰值抗剪强度对应的位移逐渐增大，这是由于锯齿高度增大导致结构面起伏度增加，从而增强其抗剪强度；同时，由于锯齿高度增大，位于锯齿部位的软弱夹层厚度也增加，进而导致结构面的延性特征增强。

锯齿高度/mm：1—0；2—20；3—40；4—50；5—60；6—80；7—100；8—120；9—130；10—150。

图5 剪切过程各阶段示意图

图6 锯齿高度与峰值切向位移的关系

当结构面切应力达到峰值强度后即进入应变软化阶段。从图5可以看出：该阶段是切应力达到峰值后的下降段，在此阶段岩体会产生宏观破坏，并且在该阶段切应力与剪切位移之间的关系曲线符合线性特征。为了描述不同锯齿高度下结构面的应变软化特征，分别对应变软化阶段的切应力和剪切位移关系进行线性拟合，得到拟合相关系数均大于0.9，说明两者高度线性相关，结果如表4所示(其中，为切向位移，为切应力，为应变软化阶段的应力下降速率)。从表4可见：当正应力相同时，应变软化阶段的应力下降速率与锯齿高度有关。应力下降速率与锯齿高度的关系如图7所示。从图7可见：随着锯齿高度增大，应变软化阶段应力下降的速率迅速减小，在锯齿高度为80 mm时达到最小值后逐渐增大，但增加的幅值小于减小的幅值。由于夹层厚度为80 mm，故当锯齿高度与夹层厚度相同时，下降段的下降速率最小。这是由于当锯齿高度小于夹层厚度时，夹层起主要抗剪作用，峰值后的切应力减小得更加迅速；当锯齿高度增大到与夹层厚度相同时，切应力降低速率减小到最低；当锯齿高度大于夹层厚度时，应力降低的速度又逐渐增大，这是因为当锯齿高度大于夹层厚度时，岩石剪切时的剪胀效应更加明显，故应变软化的速度更大。

表4 不同距齿高度下应变软化阶段剪切位移和应力的关系

图7 锯齿高度h与应变软化段应力下降速率|a|关系

经过应变软化阶段后，由于结构面锯齿被逐渐剪坏，从而导致结构面的剪切应力不断减小，剪切过程进入过渡阶段；当结构面出现宏观滑动时，其剪切应力变化较小，此时剪切行为进入残余阶段，其对应的残余强度为。峰值强度为岩石在剪切过程中切应力达到峰值时所对应的切应力，而残余强度为岩石剪切行为进入残余阶段后所对应的切应力。锯齿高度对于残余强度和峰值强度的影响如图8所示。从图8可见：在正应力相同时，峰值抗剪强度随着锯齿高度的增大而增大，峰值强度与锯齿高度呈线性关系，而残余强度在锯齿高度为0~120 mm范围内呈线性增大，但当锯齿高度大于120 mm时，残余强度基本保持不变，为0.25 MPa，此时其不随锯齿高度的增大而变化。这是由于当正应力为0.50 MPa时，在剪切过程中均发生一定程度剪胀，抗剪峰值强度主要由夹层内物质以及锯齿的高度起作用，故随着锯齿高度增大而增大。但是残余强度表征了锯齿发生宏观破坏后仍然具有的承载力，当锯齿高度超过一定值(120 mm)后主要发生滑移破坏而不会发生沿锯齿剪断的破坏，故锯齿高度大于120 mm时对残余强度基本没有影响。

1—峰值强度；2—残余强度。

图9所示为锯齿高度和残余强度与峰值强度比值的关系。从图9可见：随着锯齿高度增大，呈先增大后减小的趋势，当锯齿高度为100 mm时达到最大值。从图8可以进一步看出：当锯齿高度大于120 mm时，不同锯齿高度对应的节理残余剪切强度大致相同，为0.25 MPa，但峰值强度仍随锯齿高度的增大而增大，因此，呈先增大后减小的趋势；当锯齿高度为50~130 mm时，均大于0.5，即当锯齿高度与锯齿厚度相近时，岩石发生剪切破坏后仍具有50%以上的承载力；而当锯齿高度很小或为0 mm时，岩石剪切破坏后残余强度较低。可见，锯齿高度对于软弱结构面发生宏观破坏后的承载力有较大 影响。

为分析结构面在剪切过程中的剪胀效应，记录剪切过程中切向位移与法向位移的关系，如图10所示。从图10可以看出：法向位移随切向位移的增大而呈线性增大；锯齿高度越大，−关系曲线的斜率越大，即结构面的剪胀效应越明显。将切向位移为0~10 mm范围内的−关系曲线放大，发现当切向位移在10 mm以内时，法向位移与切向位移之间的关系呈现出一定的非线性特征，表现为呈波浪式上升，尤其是在锯齿高度较大的岩体中，波浪式上升的现象更加明显，这是由于结构面模型中有软弱夹层存在[19]。

图9 与锯齿高度的关系

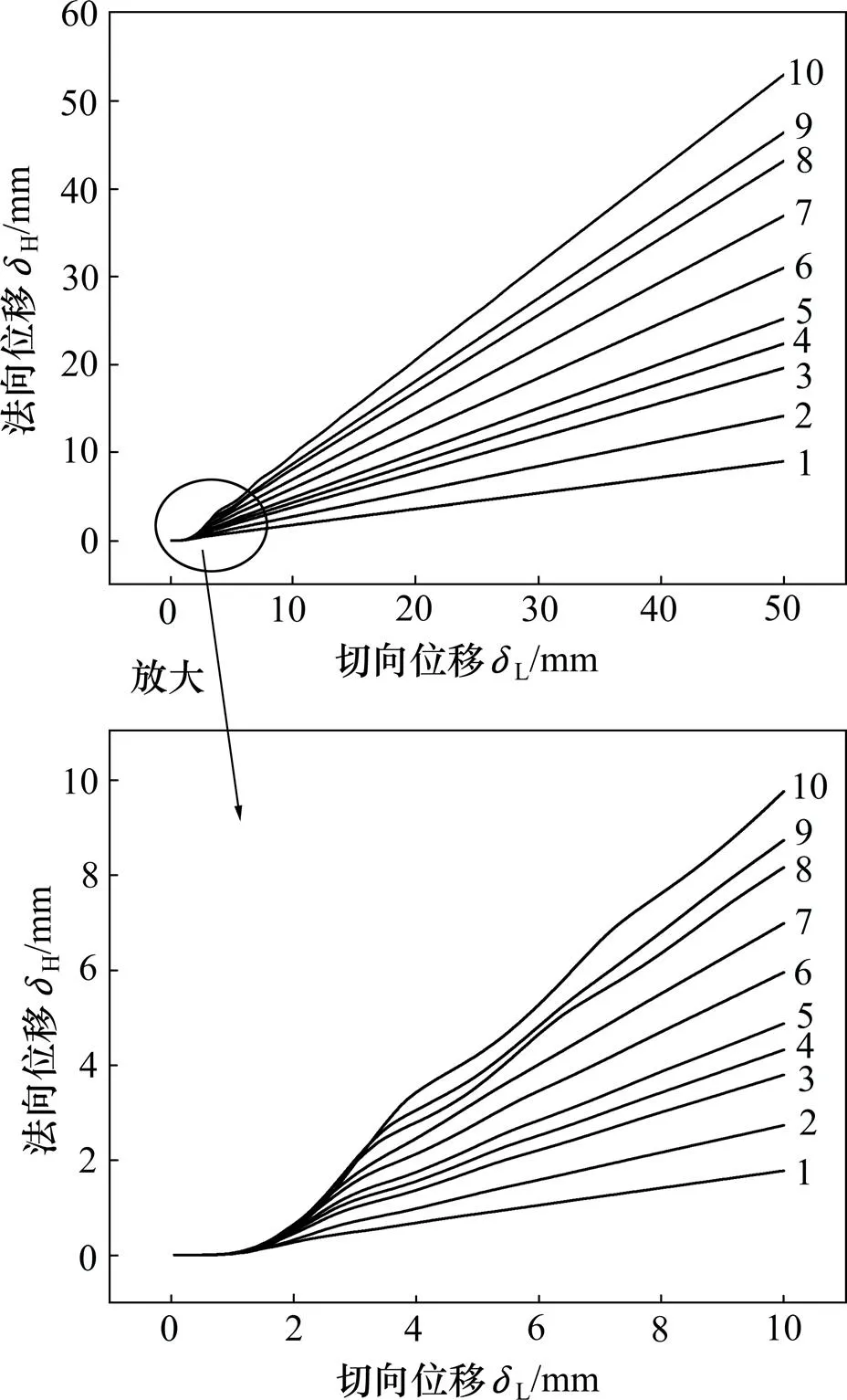
锯齿高度/mm：1—0；2—20；3—40；4—50；5—60；6—80；7—100；8—120；9—130；10—150。

2.2 法向应力对抗剪强度的影响

图12所示为不同锯齿高度下结构面的法向应力与抗剪强度的关系。从图12可以看出：当锯齿高度较大(如＞80 mm)时，结构面法向应力与抗剪强度之间呈现显著的线性关系，而当锯齿高度较小(如＜60 mm)时，两者之间的关系表现出一定的非线性特征，并且此时对应较小法向应力的剪切强度基本相同，这主要是岩体节理的软弱夹层厚度为80 mm而锯齿高度低于80 mm的岩体其抗剪强度由软弱夹层性质决定，所以，这些软弱结构面的抗剪强度相近。

锯齿高度为120 mm的结构面在不同法向应力情况下的切应力−切向位移曲线见图13。从图13可以看出：应力−位移曲线同样可分为弹性阶段、应变软化阶段、过渡阶段和残余应力阶段，并且在弹性阶段切应力−切向位移曲线的斜率大致相同，这说明对于同一锯齿高度的结构面在不同法向应力作用下表现出相同的剪切刚度；随着结构面法向应力增大，切应力−切向位移曲线在峰值后表现得更稳定，其过渡阶段的波动现象逐渐消失。

而在应变软化阶段，切应力和剪切位移的关系符合线性特征，可采用线性方程进行拟合，结果见表5。应变软化阶段应力下降速率与法向应力的关系见图14。从图14可见：随着法向应力增大，应变软化阶段的应力下降速率不断减小，并且在法向应力从0.1 MPa增大到1.5 MPa时，下降段的应力下降速率减小到初始值的1/3。这是由于法向应力增大使锯齿间的咬合更加稳固，在达到峰值强度后的切向塑性应变减小，所以，切应力下降速率减小。

锯齿高度/mm：1—0；2—20；3—40；4—50；5—60；6—80；7—100；8—120；9—130；10—150。

法向应力/MPa：1—0.1；2—0.3；3—0.5；4—0.7；5—0.9；6—1.1；7—1.3；8—1.5。

残余应力阶段法向应力对峰值抗剪强度与残余剪切强度的影响见图15。从图15可见：峰值强度与残余强度均随着法向应力的增大而呈线性增大，但残余强度增大速率较峰值强度增大速率大；结构面残余强度与峰值强度的比值随法向应力的增大而不断增大。进一步探讨法向应力对残余剪切强度与峰值抗剪强度的比值的影响，对锯齿高度为120 mm的结构面在不同法向应力情况下进行剪切模拟，所得结果如图16所示。从图16可见：随着法向应力增大，残余强度与峰值强度的比值呈现先增大后减小的趋势；当法向应力为2.1 MPa时达到最大值0.961 4，然后随法向应力的增大迅速降低到0.100 0左右。这主要是由于在峰值前，法向应力的增大可提高结构面上下岩石的咬合度，导致结构面更加稳固；当法向应力达到临界值(2.1 MPa)时，残余强度与峰值剪切强度最接近；但当法向应力大于临界值时，在较大法向应力作用下岩体结构面中软弱夹层以及周围岩石剪切破坏后被进一步破坏，所以，当法向应力较大时，残余强度与峰值剪切强度的比值骤减到0.1左右。

图14 法向应力与应变软化段应力下降速度|a|关系

表5 不同正应力下应变软化阶段应力与切位移的关系

1—峰值强度；2—残余强度。

图16 法向应力与的关系

3 结论

2) 随锯齿高度增大，应变软化阶段应力下降速率迅速减小，当锯齿高度为80 mm时，应力达到最小值后逐渐增大，但增大幅值小于减小幅值。

4) 当切向位移小于10 mm时，法向位移与切向位移之间的关系呈现一定程度的非线性特征，剪胀角与锯齿高度之间的线性关系表达式为：。

5) 当锯齿高度较大(如80 mm)时，结构面法向应力与抗剪强度之间呈现显著的线性关系，而当锯齿高度较小时二者之间的关系表现出一定的非线性特征，并且此时对应较小法向应力的剪切强度基本相同。

6) 随着法向应力增大，应变软化阶段应力下降速率不断减小，残余强度与峰值强度的比值呈先增大后减小的趋势，最大值为0.961 4。

[1] INDRARATNA B, PREMADASA W, BROWN E T. Shear strength of rock joints influenced by compacted infill[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 70(9): 296−307.

[2] LEE Y K, PARK J W, SONG J J. Model for the shear behavior of rock joints under CNL and CNS conditions[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 70(9): 252−263.

[3] SERRANO A, OLALLA C, GALINDO R A. Micromechanical basis for shear strength of rock discontinuities[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 70(9): 33−46.

[4] BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1978, 10(1/2): 1−54.

[5] LADANYI B, ARCHAMBAULT G. Simulation of shear behavior of a jointed rock mass[J]. US Symposium on Rock Mechanics, 1969, 20(11): 2359−2365.

[6] 葛修润. 岩体中节理面、软弱夹层等的力学性质和模拟分析方法(一)[J]. 岩土力学, 1979, 1(1): 54−75. GE Xiurun. The mechanical behavior and analog analytical method of joints and weak intercal ations in rock mass[J]. Rock and Soil Mechanics, 1979, 1(1): 54−75.

[7] 程强, 周德培, 封志军. 典型红层软岩软弱夹层剪切蠕变性质研究[J]. 岩石力学与工程学报, 2009, 28(Z1): 3176−3180. CHENG Qiang, ZHOU Depei, FENG Zhijun. Research on shear creep property of typical weak intercalation in redbed soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Z1): 3176−3180.

[8] 高正夏, 赵海滨. 岩体软弱夹层渗透变形试验及三维有限元数值模拟[J]. 水文地质工程地质, 2008, 35(1): 64−66, 79. GAO Zhengxia, ZHAO Haibin. Seepage deformation field test and three-dimensional finite element numerical modeling on weak intercalation in rock mass[J]. Hydrogeology and Engineering Geology, 2008, 35(1): 64−66, 79.

[9] 许宝田, 钱七虎, 阎长虹, 等. 多层软弱夹层边坡岩体稳定性及加固分析[J]. 岩石力学与工程学报, 2009, 28(Z2): 3959−3964. XU Baotian, QIAN Qihu, YAN Changhong, et al. Stability and strengthening analyses of slope rock mass containing multi-weak interlayers[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Z2): 3959−3964.

[10] 肖卫国, 兑关锁, 朱玉萍, 等. 充填单节理岩体本构模型研究[J]. 岩石力学与工程学报, 2010, 29(Z2): 3463−3468. XIAO Weiguo, DUI Guansuo, ZHU Yuping, et al. Study of constitutive model for single infilled jointed rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Z2): 3463−3468.

[11] 孙辅庭, 佘成学, 万利台. 充填水泥浆岩石节理峰值剪切强度模型[J]. 岩石力学与工程学报, 2014, 33(12): 2481−2489. SUN Futing, SHE Chengxue, WAN Litai. A peak shear strength model for cement filled rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(12): 2481−2489.

[12] 胡毅方, 彭振斌, 柳群义. 规则锯齿型软弱结构面剪切特性的数值分析[J].沈阳工业大学学报, 2012, 34(6): 710−714. HU Yifang, PENG Zhenbin, LIU Qunyi. Numerical analysis for shear characteristic of soft structure plane with regular curved edge[J]. Journal of Shenyang University of Technology, 2012, 34(6): 710−714.

[13] 廖秋林, 曾钱帮, 刘彤, 等. 基于ANSYS平台复杂地质体FLAC3D模型的自动生成[J]. 岩石力学与工程学报, 2005, 24(6): 1010−1013. LIAO Qiulin, ZENG Qianbang, LIU Tong, et al. Automatic model generation of complex geologic body with FLAC3D based on ANSYS platform[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 1010−1013.

[14] 林杭, 曹平, 李江腾, 等. 基于SURPAC的FLAC3D三维模型自动构建[J]. 中国矿业大学学报, 2008, 37(3): 339−342. LIN Hang, CAO Ping, LI Jiangtong, et al. Automatic generation of FLAC3D model based on SURPAC[J]. Journal of China University of Mining & Technology, 2008, 37(3): 339−342.

[15] 罗周全, 吴亚斌, 刘晓明, 等. 基于SURPAC的复杂地质体FLAC3D模型生成技术[J]. 岩土力学, 2008, 29(5): 1334−1338. LUO Zhouquan, WU Yabing, LIU Xiaoming, et al. FLAC3D modeling for complex geologic body based on SURPAC[J]. Rock and Soil Mechanics, 2008, 29(5): 1334−1338.

[16] 李坤, 佘成学. 灌浆节理压剪峰值抗剪强度数值试验研究[J]. 武汉大学学报(工学版), 2012, 45(5): 570−574. LI Kun, SE Chengxue. Numerical test study of peak shear strength of cement-grouted joint under compression shearing[J]. Engineering Journal of Wuhan University, 2012, 45(5): 570−574.

[17] 乌青松. 含软弱夹层红砂岩边坡水毁机理及加固研究[D]. 长沙: 中南大学资源与安全工程学院, 2014: 4. WU Qingsong. Research of red sandstone slope with weak intercalated waterlogging mechanism and strengthening[D]. Changsha: Central South University. School of Resources & Safety Engineering, 2014: 4.

[18] 水利水电科学研究院. 岩石力学参数手册[M]. 北京:水利电力出版社, 1991: 391−398. Institute of Water Resource and Hudrapower Research. Rock mechanics manual[M]. Beijing: Water Resources and Electric Power Press, 1991: 391−398.

[19] 赵文, 曹平, 章光. 岩石力学[M]. 长沙: 中南大学出版社, 2010: 71. ZHAO Wen, CAO Ping, ZHANG Guang. Rock mechanics[M]. Changsha: Central South University Press, 2010: 71.

[20] HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34(97): 1165−1186.

(编辑 陈灿华)

Influence of dentate discontinuity height on shear properties of soft structure plane

TANG Wenyu1, LIN Hang1, 2

(1. School of Resources & Safety Engineering, Central South University, Changsha 410083, China;2. State Key Laboratory for GeoMechanics and Deep Underground Engineering, China University of Mining and Technology, Xuzhou 221116, China)

In order to study the shear behavior of soft structure plane in different normal stresses and dentate discontinuity heights, a series of structure plane calculation models with different dentate discontinuity height were established with numerical method and were used to simulate the direct shear test under different normal stresses. The relationship between stress and strain before and after the peak shear strength of the structural plane was discussed. A linear relationship expression between the dilatancy angle and the dentate discontinuity height was established. The results show that with the increase of the dentate discontinuity height, the peak shear displacement shows a trend of increase and the descending speed of stress in the stage of strain softening decreases at first and then increases, and reaches the minimum when the thickness of the interlayer and the dentate discontinuity height is equal. With the increase of the dentate discontinuity height, both the peak shear strength and the residual shear strength increase linearly, but when the dentate discontinuity height reaches a certain value, the residual shear strength does not change. When the dentate discontinuity height is higher such as 80 mm, the relationship between the normal stress and the shear strength of the structure plane appears to be linear. When the dentate discontinuity is at a low height, the relationship between them shows a certain nonlinear characteristics, and at this condition the shear strength of the corresponding smaller normal stress is the same. With the increase of the normal stress, the descending speed of stress in the stage of strain softening decreases continually, and the ratio of residual strength to peak strength increases at first and then decreases, and the maximum is 0.961 4.

dentate discontinuity height; soft structure plane; shear properties; residual strength

10.11817/j.issn.1672-7207.2017.05.024

TU452

A

1672−7207(2017)05−1300−08

2016−06−10；

2016−08−22

国家自然科学基金资助项目(51474249，51374246)；中南大学“创新驱动计划”项目(2016CX019，2015CX005)；深部岩土力学与地下工程国家重点实验室开放基金资助项目(SKLGDUEK1405)；中南大学研究生创新项目(2016zzts454) (Projects(51474249, 51374246) supported by the National Natural Science Foundation of China; Projects(2016CX019, 2015CX005) supported by the Innovation Driven Project of Central South University; Project(SKLGDUEK1405) supported by the State Key Laboratory Open Fund of Deep Geomechanics and Underground Engineering; Project(2016zzts454) supported by the Graduate Student Innovation Project of Central South University)

林杭，博士，副教授，从事岩土工程理论和数值计算研究；E-mail: linhangabc@126.com