3-CRR型并联机构运动学与奇异性分析

刘知辉，牛军川，周一群



3-CRR型并联机构运动学与奇异性分析

刘知辉1, 2，牛军川1, 2，周一群1, 2

(1. 山东大学机械工程学院，山东济南，250061；2. 山东大学高效洁净机械制造教育部重点实验室，山东济南，250061)

对一种典型的具有三平移自由度的3-CRR型并联机构进行正、逆运动学求解，讨论该类型并联机构的工作空间，利用虚功原理研究该型机构运行时在动平台承受固定载荷情况下主动关节处的受力情况，定义雅克比矩阵转置矩阵的∞−范数作为评价3-CRR型并联机构承载能力与运动精度性能的指标，通过设定该指标的许用值，可得到3-CRR型并联机构性能不能满足工作要求的区域，避开该区域即可成功避开机构的奇异点，使得3-CRR型并联机构工作于正常状态，对其他并联机构的设计和综合具有指导意义。

并联机构；工作空间；奇异；虚功原理

并联机构以其刚度大、精度高、承载能力强等优点被广泛应用于飞行模拟器、工业机器人、虚拟轴机床等领域[1]。在一些情形下，完成机构的功能并不需要6个自由度，因此，近几年来少自由度并联机构开始受到越来越多的关注。相比六自由度并联机构，少自由度并联机构结构相对简单，且易于控制。国内外学者根据所需的自由度及自由度类型综合出众多类型的少自由度并联机构[2]。3-CRR型并联机构是一种典型的拥有三平移自由度的少自由度并联机构。赵铁石等[3]对静平台与动平台处运动副呈三角形布置状态下的3-CRR型并联机构的运动学进行了分析。KONG 等[4]对3个圆柱副不位于且不平行于同一平面的3-CRR型并联机构进行了研究，并提出一种各向同性的正交3-CRR型并联机构。艾永强等[5]对一种三支路特殊配置的3-CRR型并联机构进行了运动学分析。牛军川等[6]研究了基于3-CRR机构的变胞多维减振平台。马履中等[7]对一种类似于3-CRR型并联机构的3-RRC机构进行了特殊位形的分析。可见，3-CRR机构是一种比较典型的并联机构，但其运动学特性、工作空间和奇异性等并没有得到充分的重视和讨论。本文作者对圆柱副轴线位于同一平面且彼此正交或平行的3-CRR型并联机构进行分析，选取静平台处3个圆柱副中2个圆柱副的平移自由度和1个圆柱副的转动自由度作为主动输入，对其正、逆运动学进行求解，研究利用雅克比矩阵转置矩阵的∞−范数作为评价指标对3-CRR型并联机构的承载能力、运动精度和奇异性等进行评价的可行性，并进一步利用该指标对3-CRR型并联机构在几何约束下的工作空间进行划分，从而得到3-CRR型并联机构具有良好性能，可满足承载能力和定位精度条件的工作空间。关于雅克比矩阵转置矩阵的∞−范数作为并联机构承载能力与运动精度性能评价指标的讨论对于确定其他类型并联机构的可用工作空间亦有一定意义。

1 运动学分析

1.1 自由度的计算

3-CRR型并联机构存在多种变形形式，本文所分析的3-CRR并联机构如图1所示。该机构由动平台，静平台以及连接动静平台的3条相同配置的支链组成，3条支链中2条相对的支链轴线相互平行且与第3条支链垂直。

3条支链分别命名为A，B和C，如图2所示。每条支链的3个运动副自底向上分别命名为1,2,3，其中为支链名称。于1轴线与1轴线相交处建立固结于静平台的坐标系，轴垂直于静平台向上，轴沿1方向。于3轴线与3轴线相交处建立固结于动平台的坐标系，轴垂直于动平台向上，轴沿3方向。

图1 3-CRR型并联机构

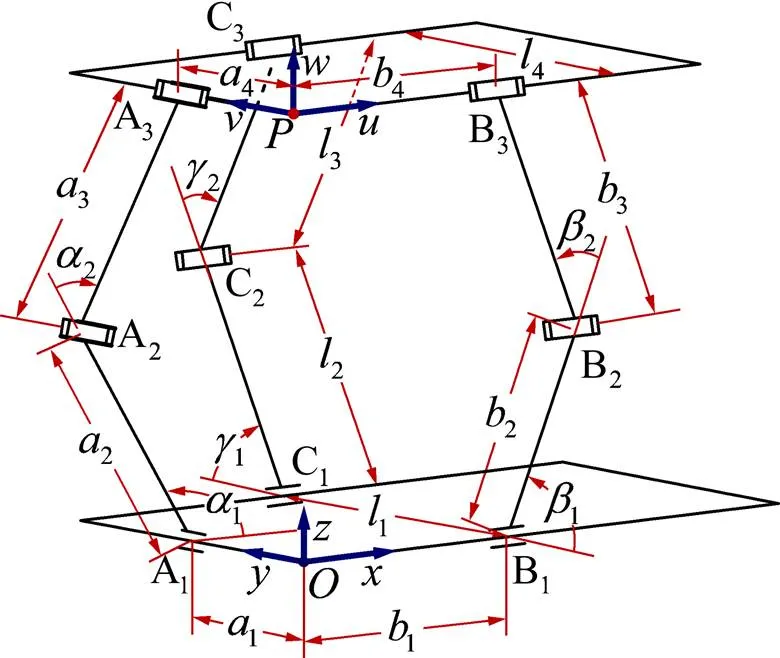
图2 3-CRR型并联机构结构简图

在坐标系中依次将支链A，B和C的各个运动副表示成螺旋，其中圆柱副可视为共轴线的转动副与移动副的组合，根据螺旋与反螺旋的互易积为零的性质，可计算出各个支链的反螺旋。各个支链的反螺旋也即各个支链对动平台的约束，计算显示3-CRR型并联机构的每条支链皆有2个线性无关的反螺旋，且皆为反力偶螺旋，也即每条支链都限制了动平台的2个转动自由度，在3条支链提供的6个反螺旋中，共有3个线性无关的反螺旋，从而过约束数为3。将过约束数代入修正后的Kutzbach-Grübler自由度计算公式[8]，可计算得出自由度=3。从而3-CRR型并联机构具有3个平移自由度，不具有姿态变化能力。

1.2 主动副的选取

上述的分析表明该机构共有3个平移自由度，因此可选取3个主动输入。对于3-CRR型并联机构，为使得机构在运行过程中有较小的惯性，主动副可设置在静平台上。主动副的选取应使得机构在主动副有确定输入的情况下亦有确定的输出，更特殊地，当主动副静止时机构的动平台也应处于静止状态。对于自由度为的并联机构，选取个运动副将其刚化，若刚化后的新机构的自由度为0，则选取的运动副可作为主动副，否则不能作为主动副。

若按照以上主动副选定原则，则主动副应在位于静平台的圆柱副中选择。在实际工程中，为设计和安装简单、运行平稳和易于控制，一般只在1个运动副上施加1个驱动。在将圆柱副视为共轴的移动副(P幅)与转动副(R副)的组合，且对于每个圆柱副只驱动其单个自由度时，主动副的选择方式可有23种。考虑到在整体结构中，B支链与C支链为对称布置，二者具有等价性，因而共有6种不同的组合方式，表1所示为所有6种主动副选用方案及对应的刚化主动副后机构的自由度。

表1 主动副组合方式

由表1可知：共有3种可行的主动副选择方案。主动副的选用对机构的工作空间、解耦性以及并联机构的承载能力具有直接影响。对于本文所分析3-CRR型并联机构，因其每条支链内的运动副轴线互相平行，若选用静平台处圆柱副的移动自由度为主动输入，则该移动方向不存在耦合现象，解耦性质的存在使得机构的运动控制相对容易，但同时也应注意到，若选取圆柱副的移动自由度作为主动输入，则该圆柱副所对应的支链将不承受向载荷，因此，若机构在工作时向承受较大载荷，则需考虑增加主动输入中转动副的数量。若单条支链即可承受机构工作时向载荷，则在可行的3种主动副选择方案中可选用方案2，即2P1R作为主动输入，在该主动副方案下，机构的2个移动方向都将不存在耦合现象，机构拥有较好的解耦性。

1.3 正运动学分析

正运动学给出在主动副位置或速度已知的情况下末端操作器的位置或速度[9]。在选用方案2作为主动输入时，设主动副处的位移为，选定固结于动平台的坐标系原点作为动平台参考点，向量为参考点在静平台参考系中的坐标，即

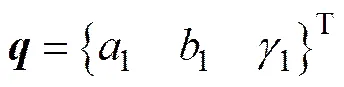
(2)

根据几何关系，可以分别以A，B和C3条支链尺寸为参数，得到点在坐标系中的坐标。

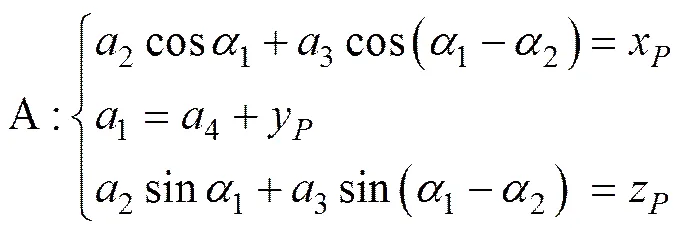
(4)

(5)

据式(3)和(4)可得：

(7)

可见：3-CRR型并联机构在选用主动副组合方案2时，正运动学关系在向和向皆为完全解耦。

解式(8)可得

(9)

(a) 式(9)中取“−”的解；(b) 式(9)中取“+”的解

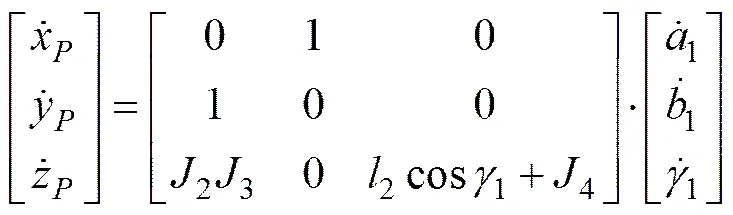
式(10)可简写为

(11)

式中，1为机构的一阶运动影响系数矩阵。

1.4 逆运动学分析

与正运动学相反，逆运动学给出在末端操作器位置或速度已知的情况下主动副位置或速度。由式(3)和(4)可知：

(13)

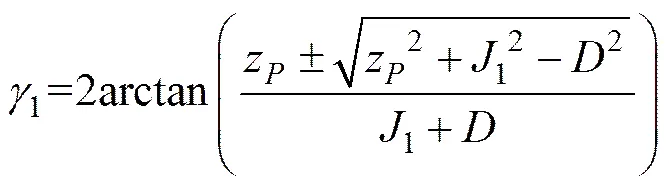
式(14)中正负号的选择与圆柱副1的运动范围有关，如图4所示，在给定动平台位置时，利用逆解关系可求得圆柱副1处角度有2个解与其对应。图4(a)所示为式(14)取“−”时的姿态，图4(b)所示为式(14)取“+”时的姿态。

(a) 式(14)中取“−”时的姿态；(b) 式(14)中取“+”时的姿态

图4 2种不同的逆解

Fig. 4 Two kinds of different inverse solutions

图2中的其他中间量可以按照1处转角的求解方法依次求得。A和B支链圆柱副处转角的逆解解析表达式皆与式(14)有类似的结构，也即有“”2个解。从而求得的逆解结果共有2×2×2种。图5所示为逆解对应的姿态，每种姿态以，和的顺序取逆解表达式中“+”或“−”的规则命名。

图5所示为8种逆解姿态仅是在几何约束条件下的可行逆解。由于运动的连续性，3-CRR型并联机构在动平台位置确定的情况下其逆解是唯一确定的，且取何种逆解与机构的初始状态以及运动副的运动范围有关。由图5可见：当支链中间的转动副位于“内部”即动平台正下方时，3-CRR型并联机构在运行时支链间可能发生干涉，因此，本文选取机构的结构参数以及运动副运动范围参数使得3-CRR型并联机构运行于图5(a)所示状态。

图5 3-CRR型并联机构的8种逆解

2 工作空间

机构的工作空间是机构末端操作器参考点所能到达的位置点的集合[10]。对于所分析的3-CRR型并联机构，也即动平台处点可到达位置的集合。由上述分析可知：在选取2个移动自由度和1个转动自由度作为主动输入的情况下，3-CRR型并联机构在和向都具有完全解耦性，但向的位置与速度仍同时与圆柱副1和圆柱副1有关，也即在向存在耦合。该耦合的存在使得不易通过解析法在主动副活动范围确定的情况下获得3-CRR型并联机构的工作空间。可采用数值解法对工作空间进行求解，对3-CRR型并联机构可能的工作空间离散后进行逐点扫描，对扫描到的点利用逆运动学关系求解其对应的主动输入，若

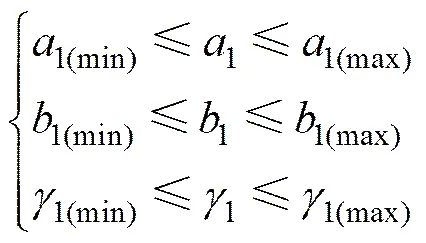
则可认为被扫描到的点位于主动输入范围内，该点位于工作空间内，予以保留。最终扫描得到的点集形成的包络体即为其工作空间。若离散足够细密，则所得到工作空间也足够精确。取结构参数和主动副运动范围为2=2=2=100 mm，3=3=3=50 mm，1=4=100 mm，4=50 mm，4=60 mm，0≤1≤100 mm，0≤1≤100 mm，0≤≤π/2 rad，此时，3-CRR型并联机构工作于图5(a)所示状态，支链间以及支链与动平台间不发生运动干涉。利用上述方法得到的工作空间如图6所示。

(a) 轴侧图；(b)向视图；(c)向视图；(d)向视图

图6 3-CRR型并联机构工作空间

Fig. 6 Workspace of 3-CRR parallel mechanism

由图6可知：3-CRR型并联机构的工作空间为一“拉伸体”，若在工作空间内沿方向设置若干与平面平行的平面作为截面与工作空间相交，则截面为固定形状，该特性正是3-CRR型并联机构在方向完全解耦的体现，动平台的方向虽也与主动副处位移完全解耦，但由于向位移与1和的耦合使得向位移与向位移之间亦存在耦合，故在方向无这一特性。

利用上述数值方法判断3-CRR型并联机构仅是在几何约束下3-CRR型并联机构的工作空间，即理论上3-CRR型并联机构动平台参考点所有可达位置，但由于奇异性的存在，使得3-CRR型并联机构在处于工作空间内的某些位置时性能较差，失去并联机构运动精度高、承载能力强等优点。

3 奇异性分析

GOSSELIN等[11]将奇异分为位形奇异、边界奇异与构型奇异。其中位形奇异发生在工作空间内部，且发生时并联机构失去控制，对机构影响最大。当位形奇异发生时，若动平台处承受载荷||||≠0，则主动副处的载荷||||→∞，即运动学奇异发生时，会产生静力学奇异，反之亦然[12]，从而静力学奇异与运动学奇异具有等价性。对于本文的3-CRR型并联机构，若忽略摩擦和阻尼效应，则由虚功原理可知

(17)

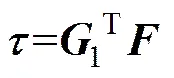
(a) 支链的受力；(b) 机构的受力

图7 主动副处的广义力

Fig. 7 Generalized force in active joints

考察在∞−范数意义下单位力作用于动平台时机构的主动副处的广义力*的大小，定义关于动平台位置的力传递系数函数：

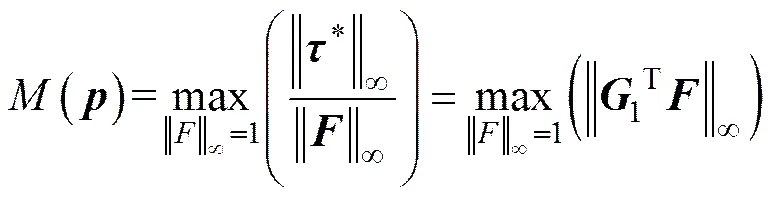
()的上确界为从属于向量∞−范数的矩阵算子范数，也即的∞−范数，从而，

(20)

即

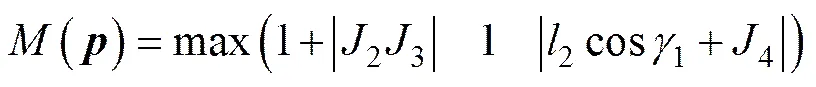
将式(11)对时间积分，可得

当1可逆时，，若3-CRR型并联机构在按照预定轨迹运行中，主动副处发生微小扰动，偏离预定的位置δ，则动平台偏移预定位置为

(23)

由矩阵范数与向量范数的相容性可知

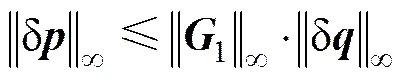
且

(25)

由式(24)和式(25)可得

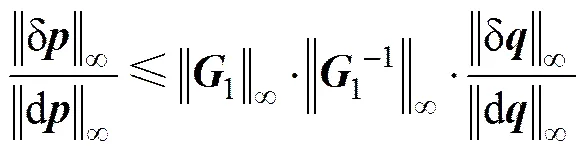
式(26)的物理意义为：当主动副处发生扰动时，在∞−范数意义下，主动副的相对误差与动平台的相对误差之间的关系由一阶运动影响系数矩阵1的条件数确定。1的条件数反映了相对误差放大系数的上确界。由一阶运动影响系数矩阵1的形式可知，其逆矩阵的∞−条件数大于1，从而

(27)

由矩阵范数的等价性可知

式中：1和2皆为正数；()=11。从而当()较大时，3-CRR型并联机构的放大系数也较大，并联机构精度较高的优点不再存在。

以上讨论表明：()可同时作为评价3-CRR型并联机构力传递特性与相对误差传递特性的指标，在其他条件保持不变的情况下，()较大表明主动副处的受力较大，机构的运动误差亦较大，即此时3-CRR型并联机构性能较差。

利用基于逆解关系的数值解法求得的3-CRR型并联机构的工作空间仅考虑了几何约束。为使得3-CRR型机构充分体现并联机构承载能力强、精度高的优点，应对()予以限制。当根据3-CRR型并联机构工作条件给定可接受的()的最大值max后，对于工作空间内的位置，若()＞max，则该位置虽位于工作空间中，但由于()超过限制，承载能力与运动精度无法满足要求，处于该点的3-CRR型并联机构仍应被视为失效状态而不可用。如图8所示，使3-CRR型并联机构工作于非失效区域不仅能使其性能满足要求，而且能使其免于奇异。

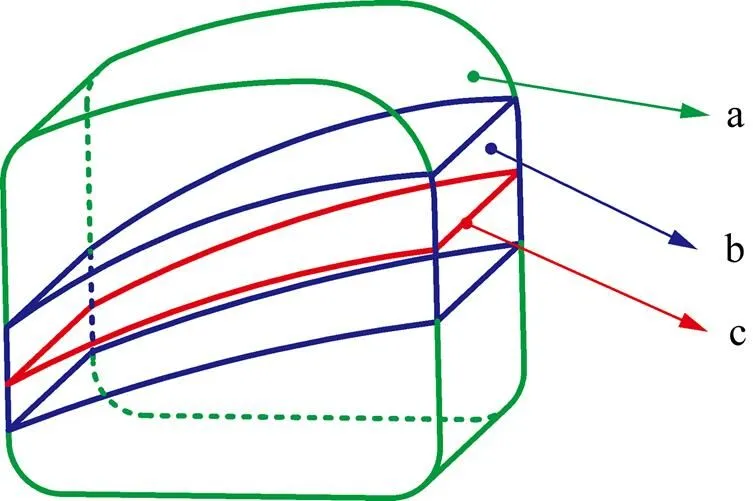
(a) 工作空间；(b) M(p)＞Mmax区域；(c) 奇异位置曲面

仍以工作空间求解中所使用的参数作为实例，给定不同的max绘制失效区域。图9~11右侧图中2条曲线之间的区域即为失效区域。

由于该机构在方向的解耦性，失效区域也有与工作空间类似的结构，沿方向为恒定截面，沿方向呈“拉伸”状。该区域内()＞max，无法满足承载能力与运动精度的要求。

由图9~11可知：3-CRR型并联机构在几何约束下的工作空间被失效区域分成多个部分，当给定3-CRR型并联机构可正常工作时的max后，3-CRR型并联机构只能工作在被失效区域划分开的多个部分的其中之一。随着max增大，可用区域逐渐增大，而失效区域逐渐减小；随着max不断增大，失效区域最终将收敛于奇异曲面。若定义关于位置的函数

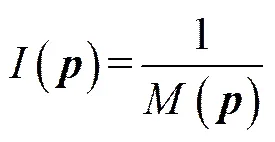
在对3-CRR型并联机构进行轨迹规划时，应根据工作性质对机构性能的具体要求设定max，并通过设定主动副的运动范围使得动平台运动时的轨迹不进入失效区域。

(a) 工作空间与失效区域；(b) 工作空间与失效区域截面

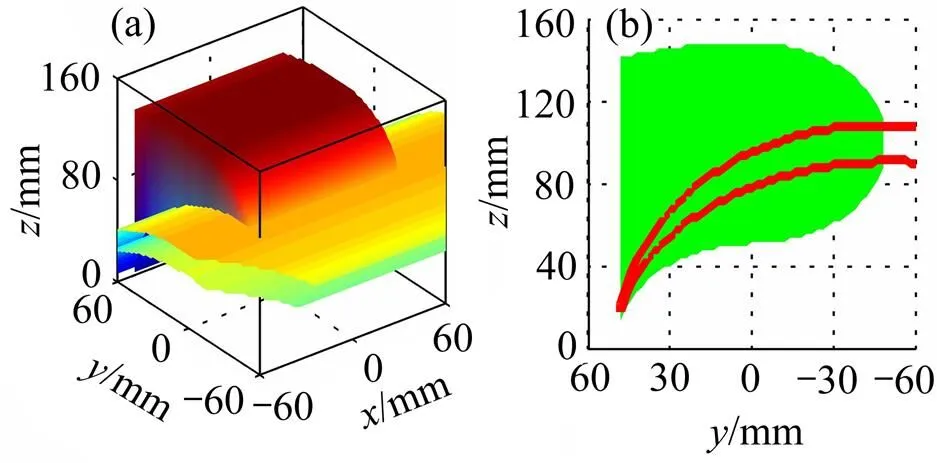
(a) 工作空间与失效区域；(b) 工作空间与失效区域截面

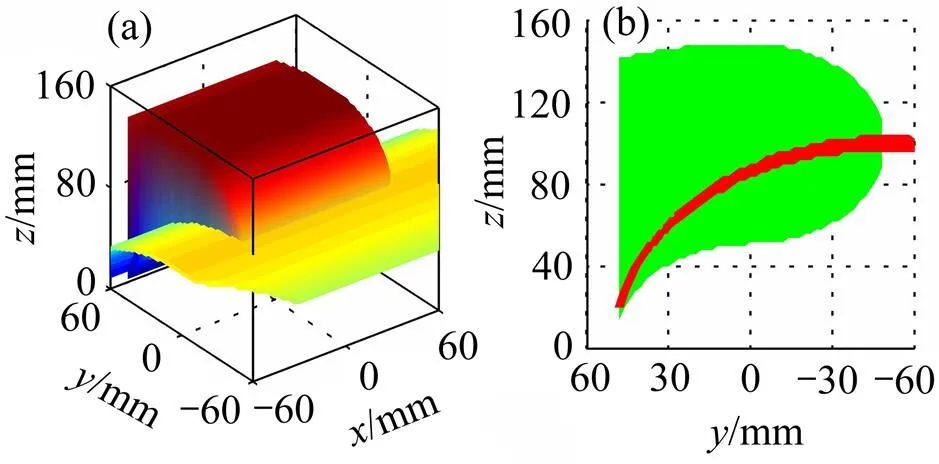
(a) 工作空间与失效区域；(b) 工作空间与失效区域截面

4 结论

1) 对主动副轴位于同一平面且彼此平行或垂直布置的3-CRR型并联机构进行分析，对主动副的选取进行了讨论，得到了一种具有良好解耦性的并联机构，并对其进行了运动学分析。基于其逆运动学关系，借助数值解法求得其工作空间。其工作空间在某一移动方向呈“拉伸”状，印证了在选定的主动副方案下3-CRR型并联机构具有良好的解耦性这一特性。

2) 提出了采用力的传递系数函数用以评估力的传递特性，并借助该函数对基于几何约束得到的工作空间进行了研究，得出几何约束下的工作空间并非全部为可用空间，得出的力传递系数函数可用于评估3-CRR型并联机构承载能力与运动精度。当并联机构若奇异位置不易求得时，只需在轨迹规划时，避开由该函数确定的并联机构失效区域即可使得机构免于奇异并获得在承载能力和运动精度条件上满足要求的轨迹。

[1] 路懿, 胡波. 少自由度并联机构研究进展[J]. 燕山大学学报, 2011, 35(5): 377−384. LU Yi, HU Bo. Development evaluation of limited-DOF parallel manipulators[J]. Journal of Yanshan University, 2011, 35(5): 377−384.

[2] 李秦川. 对称少自由度并联机器人型综合理论及新机型综合[D]. 秦皇岛: 燕山大学机械工程学院, 2003: 10−13. LI Qinchuan. Type synthesis theory of lower-mobility parallel mechanisms and synthesis of new architectures[D]. Qinhuangdao: Yanshan University. Mechanism Engineering Institute, 2003: 10−13.

[3] 赵铁石, 黄真. 一种三维移动并联平台机构的运动学分析[J]. 中国机械工程, 2001, 12(6): 613−616. ZHAO Tieshi, HUANG Zhen. Kinematics of a three-dimension translational parallel platform mechanism[J]. China Mechanical Engineering, 2001, 12(6): 613−616.

[4] KONG Xianwen, GOSSELIN Clement. Kinematics and singularity analysis of a novel type of 3-CRR 3-DOF translational parallel manipulator[J]. The International Journal of Robotics Research, 2002, 21(9): 791−798.

[5] 艾永强, 马履中. 一种三平移并联机器人运动学分析[J]. 机械设计, 2005, 22(11): 19−22. AI Yongqiang, MA Lüzhong. A kind of kinematical analysis on parallel robot with three translations[J]. Journal of Machine Design, 2005, 22(11): 19−22.

[6] 牛军川, 杨峰, 李勇. 基于变胞并联机构的多维隔振研究[J]. 振动与冲击, 2014, 33(7): 206−209, 226. NIU Junchuan, YANG Feng, LI Yong. Multi-dimensional vibration isolation based on metamorphic parallel mechanism[J]. Journal of Vibration and Shock, 2014, 33(7): 206−209, 226.

[7] 马履中, 尹小琴, 杨廷力. 新型3{R∥R∥C}三平移并联机器人机构的特殊位形分析[J]. 江苏大学学报(自然科学版), 2002, 23(2): 43−45. MA Lüzhong, YIN Xiaoqin, YANG Tingli. Analysis of special configuration of a new 3-DOF translational parallel robot mechanism {3-R∥R∥C}[J]. Journal of Jiangsu University (Natural Science Edition), 2002, 23(2): 43−45.

[8] 杨峰. 一种可变胞并联机构的多维隔振平台研究[D]. 济南: 山东大学机械工程学院, 2013: 23−37. YANG Feng. Research on multi-dim vibration isolating device based on metamorphic parallel mechanism[D]. Jinan: Shandong University. School of Mechanical Engineering, 2013: 23−37.

[9] 黄真. 高等空间机构学[M]. 北京: 高等教育出版社, 2006: 115−138. HUANG Zhen. Advanced spatial mechanism[M]. Beijing: Higher Education Press: 115−138.

[10] PATEL Y D, GEORGE P M. Simulation of kinematic and workspace analysis of 3-PRS parallel manipulator[J]. International Journal of Modeling. Simulation and Scientific Computing, 2015, 6(1): 1550007−1550012.

[11] GOSSELIN C, ANGELES J. Singularity analysis of closed-loop kinematic chains[J]. IEEE Transactions on Robotics and Automation, 1990, 6(3): 281−290.

[12] 曹永刚, 张玉茹. 6-RSS型并联机构奇异性分析[J]. 机械工程学报, 2008, 44(6): 79−87. CAO Yonggang, ZHANG Yuru. Singularity analysis for 6-RSS parallel mechanism[J]. Chinese Journal of Mechanical Engineering, 2008, 44(6): 79−87.

(编辑 陈爱华)

Kinematics and singularity analysis of 3-CRR parallel mechanism

LIU Zhihui1, 2, NIU Junchuan1, 2, ZHOU Yiqun1, 2

(1. School of Mechanical Engineering, Shandong University, Jinan 250061, China;2. Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Shandong University, Jinan 250061, China)

A classical parallel 3-CRR mechanism with 3 degrees of freedom was presented, and its forward and inverse kinematics were derived respectively. Furthermore, the workspace was studied and illustrated graphically. The relationship between the force applied on the moving platform and the resultant force on the active joints was studied by the principle of virtual work. The infinite norm of the transpose of the Jacobin matrices was defined as the index to evaluate the capacity of carrying and the kinematic accuracy of 3-CRR parallel mechanism. The restricted positions where the index is over the allowable value is found, and then the trajectory can be singularity free by keeping away from these restricted positions. The work is very meaningful and useful for the design and synthesis of the other parallel mechanisms.

parallel mechanism; workspace; singularity; principle of virtual work

10.11817/j.issn.1672-7207.2017.05.010

TH113.2

A

1672−7207(2017)05−1190−08

2016−08−28；

2016−09−22

国家自然科学基金资助项目(51275275，51675306)；山东省优秀中青年科学家科研奖励基金资助项目(BS2010ZZ006) (Projects(51275275, 51675306) supported by the National Natural Science Foundation of China; Project(BS2010ZZ006) supported by the Shandong Young Scientists Award Fund)

牛军川，博士，教授，从事振动噪声控制、机械系统动力学和功率流有限元法等研究；E-mail: niujc@sdu.edu.cn