基于自主探究学习培养学生几何思维能力的实践
2017-06-12张新桂
张新桂
摘要:初中几何是数学教学的难点之一。在教学过程中,教师除了让学生掌握课本中所列知识和方法外,还要让学生理解其来龙去脉,培养学生的几何思维能力。探究性学习是几何知识学习的一种重要方式,教师可通过观察、讨论、交流、归纳、分析,帮助学生在探究合作中形成数学思维能力。
关键词:自主探究学习;初中数学;几何;教学;思维能力
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2017)04-0127
初中几何是数学教学的难点之一。在教学过程中,教师除了让学生掌握课本中所列知识和方法外,还要让学生理解其来龙去脉,培养学生的几何思维能力。那么,到底怎样培养学生的几何思维能力呢?笔者认为,探究性学习是几何知识学习的一种重要方式,教师可通过观察、讨论、交流、归纳、分析,帮助学生在探究合作中形成数学思维能力。
一、在自主探究中加强对创新精神的培养
郑君文在《数学学习论》中提出三项策略:1. 解决问题的活动由学生独立完成,教师的指导作用应体现在为学生创设情境、启迪思维、引导方向上;2. 创造性的训练,要体现在具体解决问题的过程中;3. 在解决问题的过程中,要尽量通过问题的选择、提法和安排来激发学生的积极性和创造力。在教学中,为了使学生快快乐乐学数学,教师需在课堂上多鼓励学生自主思考、自主发现,并敢于批评争论和质疑教师与课本,尽最大可能为学生营造宽松的学习空间。
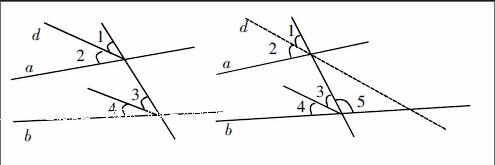
案例1:在讲“相交线中的角”时,很多学生对于稍复杂的图形便容易搞错,如图,∠1与∠3是同位角吗?∠2与∠4是同位角吗?
分析:这是一道课本的练习题,不少学生都认为∠2与∠4是同位角,出现这种错误的原因主要是对同位角的位置特点不太理解,这就要求学生首先要回想起同位角的定义,然后看图,分清所判断的两个角是哪两条直线被另外哪条直线所截而成的,从而辨认出同位角。大部分学生都是按照笔者所说的方法去完成这道题,较常规,但有一名学生提出自己的见解,他按第二个图形所示,把线d延长,与线b相交形成∠5,他认为由线a、b、d构成的角中,∠2与∠5才是同位角,非∠2与∠4。
在课上,笔者马上对这位学生给予充分肯定,并指出这种方法令人耳目一新,连教师也未曾想到,真让人佩服。
二、运用教材设置探究而不拘泥于教材
新课程标准指出:“教师不仅是课程的实施者,而且也是课程的研究、建设和资源开发的重要力量”。教师不仅是教科书的执行者,还是教学方案的开发者,即教师是“用教科书教,而不是教教科书”。因此,在数学课堂教学中,教师必须准确把握新教材的内容和要求,结合学生实际的认知水平和经验,结合本校的教学条件和教学环境,对教材进行大胆改造,做到“用教材而不拘泥于教材”。
教材在每一章都用实际背景引入,有时教师可以根据各个地方的实际情况,改用学生熟悉的例子,或者在讲课中有时也可以根据教师自己的理解调整教学内容的先后顺序。
三、自主探究中不忘紧扣双基
新教材也是要求在掌握数学基础知识与基本技能的前提下,去提高学生的创新能力。比如线段、角、三角形等一些几何的基础知识就必须要求学生熟练掌握。另外,数学必要的实践练习不能少,有些几何思想不通过实践是“探究”不出来的,更谈不上是转换成能力了。
案例2:课本“三角形”学习中,只简单介绍了三角形的一些基础知识,所以在教学过程中就有必要灵活处理教材,适当加强学生的练习。有这样一道练习题:在△ABC中,AC=12cm,AB=8cm,那么BC的最大长度应小于多少?最小的长度应该满足什么条件呢?
分析:这是一道涉及三角形三边关系的题目,第一个问题只要根据课本结论“三角形的两边之和大于第三边”就可以得到答案,但第二个问题就有一些难度,于是笔者先要求学生按第一个问题的方法去推理,这就需要分类讨论,比较麻烦,但学生也可以得出BC>4cm的结论,这时还可以引导学生归纳出BC>AC-AB的结论,再通过其他几道例题的练习得出“两边之差小于第三边”的规律。
四、淡化探究形式,加强学法指导
新教材的理念要求为学生提供自主探索、交流合作的机会,并强调使用现代教育技术进行教学,但不能矫枉过正,不能说没有用到“高科技”的课就不是一节好课。其实,课程改革也是强调教学方法的多样化。因此,教师要加强学法的指导,积极引导学生探索和发现。教师不应把数学仅当做一个已经完成了的形式结论来教,不应局限于讲各种定义、规则、方法解答“灌输”给学生,而是要创造条件,让学生在学习的过程中,用自己的体会与思维方式探索数学知识。
同时,教师在課堂上还要有意识地“暴露”数学分析的思维过程。数学教学是一种“过程教学”,教师应以“暴露”思维过程的方式着手进行课堂教学,教会学生怎样思考,并在思考的过程中想到要用哪些方法,怎样运用这些方法,最后如何解决问题。若在多种解法的情况下,学生应选择哪种解法,选择的方法好在哪里等,这些都要“暴露”出来。让学生领悟思维过程是实现“未知”到“已知”的桥梁。为此,教师必须精心“设计”问题,适时给学生“制造”一些思维受阻的情境,让学生在课堂上有足够的思维时间和空间,并让学生深思熟虑、穷本溯源,在思索中领悟数学的真谛,在思考中不断发现、不断创新。
总之,在学习几何的过程中,教师要充分尊重学生的主体地位,激发学生的探究欲望,在合作探究中培养学生的数学思维能力。
(作者单位:浙江省义乌市廿三里初中 322000)
