改进遗传算法在Claus脱硫反应动力学研究中的应用

黄 瑜，刘增让，马宏方，钱炜鑫，朱 秦，达建文，曹发海

1.华东理工大学大型工业反应器工程教育部工程研究中心，上海 200237；2.中国石油化工股份有限公司齐鲁分公司研究院，山东 淄博 255400

随着环保法规的日趋严格，工业装置中含硫酸性气的处理回收技术日益受到关注。Claus工艺是目前石油化工和煤化工装置中含硫气体处理的主要工艺之一[1]。该工艺是将含硫酸性气与空气按一定配比混合后进入反应炉，以H2S在空气中的不完全燃烧为基础，使Claus反应器中H2S/SO2之比达到适当比例，再通过SO2和H2S反应生成硫磺和水，使H2S最大限度转化为硫磺。

工业装置中Claus工艺通常包括Claus热转化、Claus催化转化、产品硫液化、液硫脱气、尾气加氢等几个不同的转化阶段[2,3]，其中催化转化阶段是整个工艺的核心[4]。催化转化阶段的主要反应是：

因热转化阶段中硫化物会和气体中的甲烷反应生成少量的CS2[5]，催化转化阶段还存在以下反应：

然而，传统的Claus脱硫反应动力学研究并未考虑原料气中CS2水解反应的影响[6,7]，可能会在反应器开发和放大过程中带来计算结果的偏差。本工作基于传统的Claus脱硫反应动力学模型，通过引入修正参数β来修正原料气中CS2存在对反应速率的影响，并采用改进遗传算法对动力学模型参数进行估值，最后对所建立的动力学模型进行统计检验和残差分析。

1 反应动力学

对于Claus催化转化主反应，根据定义，SO2的转化率为：

由式（1）计量反应式可知：

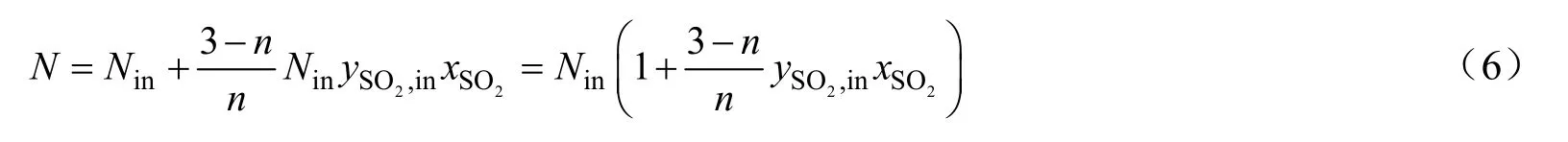
则：

SO2消耗动速率为：

而：

代入上式得：

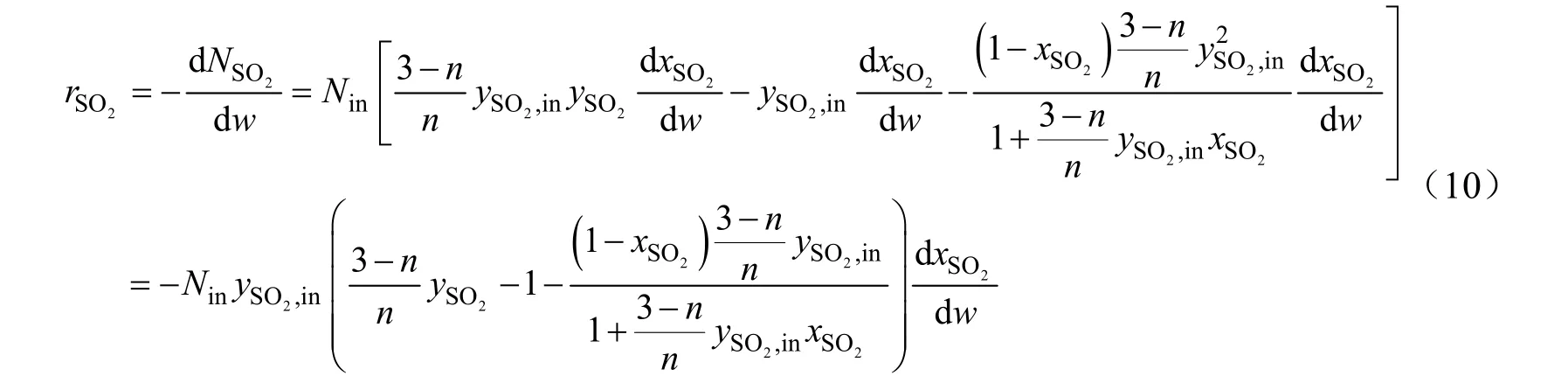
即：

文献报道的动力学方程形式主要有6种[8,9]：

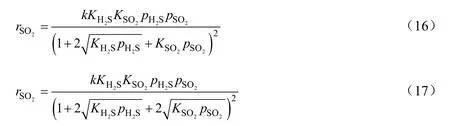
上述的动力学方程只考虑了主反应式。由于有CS2的存在，反应式（2）～（4）会生成H2S，这将影响反应动力学，需要建立新的反映复杂反应体系的动力学模型。由于CS2的存在提高了体系中的H2S浓度，在综合考虑了CS2的浓度对反应速率的影响以及模型的适应性后，提出了引入修正参数β对原有动力学模型进行修正，即：

修正参数β的存在是为了体现系统中CS2的影响，要求当CS2浓度为0时，β等于0。因此，设定β的表达式为：

其中a，b0，b1，b2，b3都为待定参数。式（12）～（17）动力学方程中，k为反应速率常数：

Ki为吸附平衡常数：

其中，k0，K0i，E，Ei都是模型待定参数。通过对式（12）～（17）的模型进行考查和检验，其中式（13）所表示的动力学模型与实验数据吻合度最高，因此，选取式（13）所表示的动力学模型为Claus脱硫动力学形式。结合式（18），建立动力学模型为：

2 算法改进

可用于反应动力学模型参数拟合的常规算法有马夸持法、单纯形法、共轭法和最速下降法等，它们被统称为局部最优化算法；而遗传算法、禁忌算法、模拟退火算法等解决了传统算法的局限性问题，可以获得全取值域内的最优解[10,11]，因此也被称为全局最优化算法。马夸特算法具有对初值敏感性较低，求解精度较高的特点，遗传算法采用变异和杂交的方式来获得全局上的最优解。本工作选取其作为局部最优化算法与遗传算法进行结合。

本工作对简单遗传算法进行改进，以保证最后可以获得全局最优解。本工作中的种群不再单纯随机产生，产生过程通过以下步骤进行：a、随机生成种群数目为n的初始种群。b、对初始种群中的个体做适应性检验，获得适应性最好的个体x。c、在新一代种群中，保留上一代的最优个体x，再由最优个体x变异产生出m个新的个体，剩下的n-m-1个新个体随机产生，产生新一代种群。d、新一代种群中，以一定概率，个体之间发生交配和变异，产生种群数目为n的下一代种群，其中上一代中的最优个体x不参加个体间的交配和变异。

将遗传算法与局部最优化算法结合，能够获得动力学模型参数在全局范围上的最优解，改进后的算法稳定性和适应性都比传统的遗传算法要好。计算流程框图如图1所示。

图1 动力学估值计算流程Fig.1 The calculation diagram for kinetic parameter estimation

3 动力学实验

Claus脱硫反应在固定床管式反应器中进行，该反应器由内径为10 mm的不锈钢管制成，反应器的高度为120 mm。所采用的LS-300催化剂（80～100目）是一种高强度、比表面积较大的Al2O3基Claus脱硫反应催化剂，催化剂的装填量为10 mL。气体产物采用日本岛津GC-2014气相色谱仪在线分析，用GDX-301担体进行硫化物的定量分析。反应器操作压力为0.15 MPa，以氮气为载气，考察了不同操作条件（反应温度、气体组成以及反应空速）对反应的影响，操作条件如表1所示。

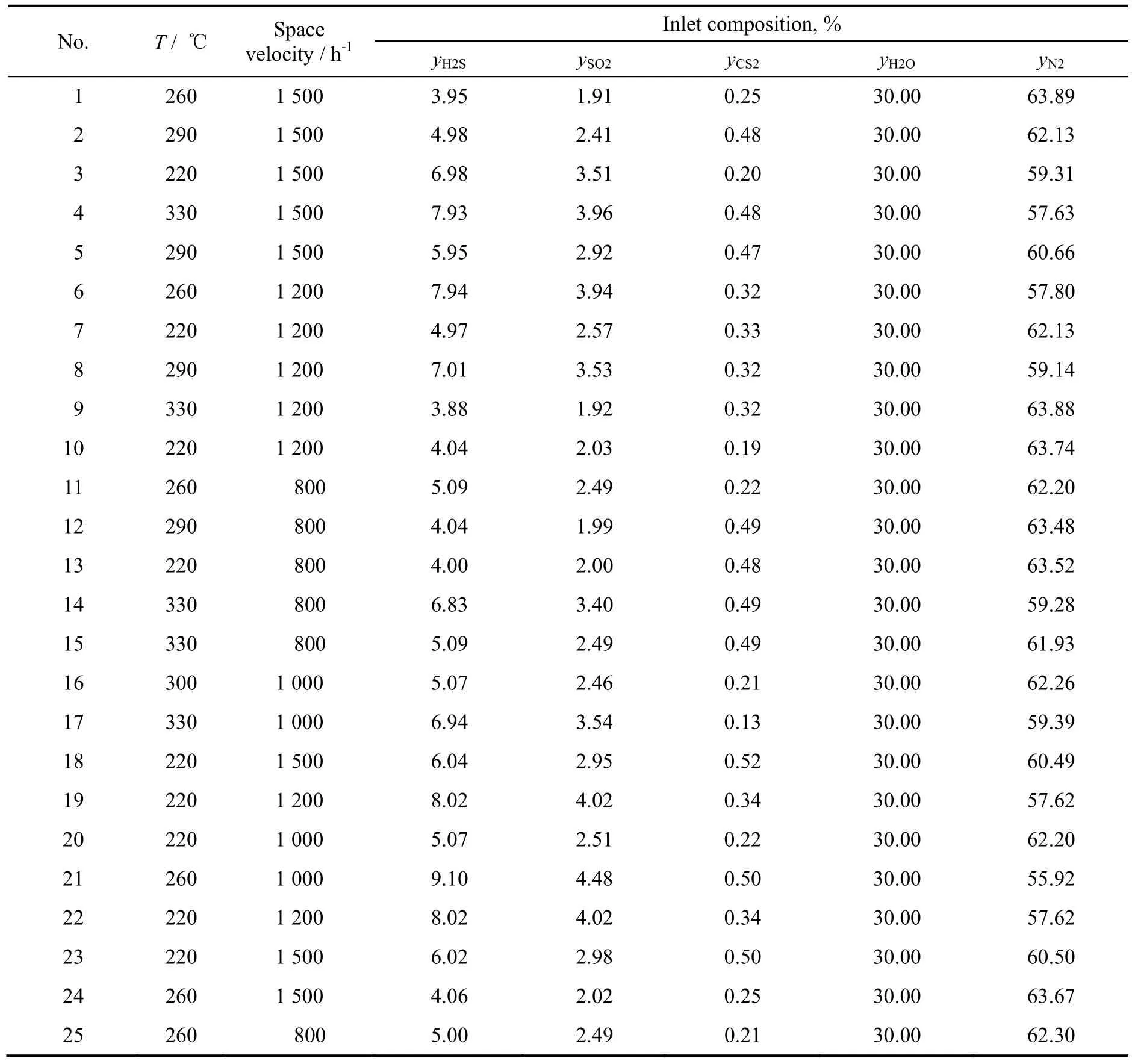
表1 动力学实验操作条件Table 1 Operating conditions of the kinetic tests

4 结果与讨论

Claus脱硫动力学模型中待定参数数为11个。由式（22）可知，所建立的Claus脱硫动力学模型为SO2转化率模型。因此，参数估值的目标函数为反应器出口SO2转化率的计算值与实验值的残差平方和S。

表2 反应器出口组成与SO2转化率Table 2 The composition of reactor outlet gas and SO2 conversion

气固相催化反应内扩散的影响通常用内部效率因子来评估。当催化剂组成一定时内部效率因子只与催化剂粒径有关。前期实验研究表明当催化剂粒径为80～100目时，脱硫效率不再随催化剂粒径变化而改变，可认为内扩散的影响已消除。动力学实验中反应器的出口组成和SO2转化率如表2所示。将表2中的数据代入式（22），采用改进遗传算法结合马夸特算法进行动力学参数估值。改进遗传算法中初始种群随机生成，采用实数编码形式。无论变异或是杂交，在种群中始终保留上一代得到的最优个体。参数估值结果如下：

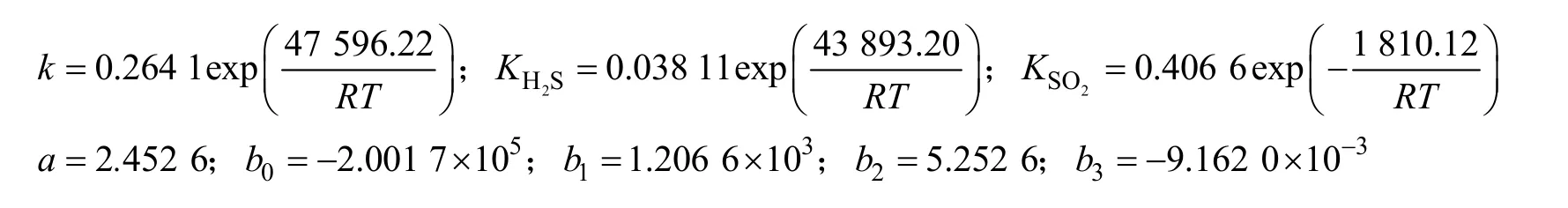
对所建立的Claus脱硫反应动力学模型进行统计检验，结果如表3所示。表3中，M是动力学实验次数，MP是参数个数，F为模型回归均方和与残差均方和的比。

表3 模型统计检验结果表Table 3 The results of the statistic test

其中：

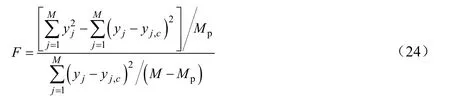
ρ2为决定性指标：

F0.05是显著水平为5%的相应自由度下的F值。一般认为，当F大于10F0.05、ρ2大于0.9时，所建立的模型是适定的。由表3的模型统计检验可知，动力学方程（22）是适定的。

对反应器出口SO2转化率的实验值与计算值进行残差分析，并与不加参数β修正得到的计算值进行比较。如图2所示，实验值与模型计算值均匀分布在对角线两侧。反应器出口转化率的误差分布如图3所示。通过对比可以看出，在引入参数β进行修正后，模型计算结果与实测值吻合度更好，误差分布也更均匀，说明参数β的引入提高了模型计算的准确度。所有实验点的相对误差都在±5%以内，且在实验范围内分布较均匀，模型计算值与实验值吻合良好，因此所得到的动力学模型是适定的。

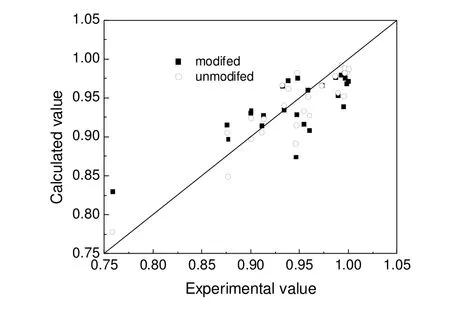
图2 反应器出口SO2转化率实验值与计算值的比较Fig.2 Comparison of the experimental and the calculation results of SO2 conversion at reactor outlet

图3 SO2转化率误差分布Fig.3 The error distribution of SO2 conversion

5 结 论

本工作在Claus脱硫反应动力学模型中引入了修正参数β来修正原料气中CS2存在对反应速率的影响，并采用改进遗传算法对25组实验数据进行了动力学模型参数估值，从而建立了消除内扩散影响的宏观反应动力学模型：

其中各参数值为：

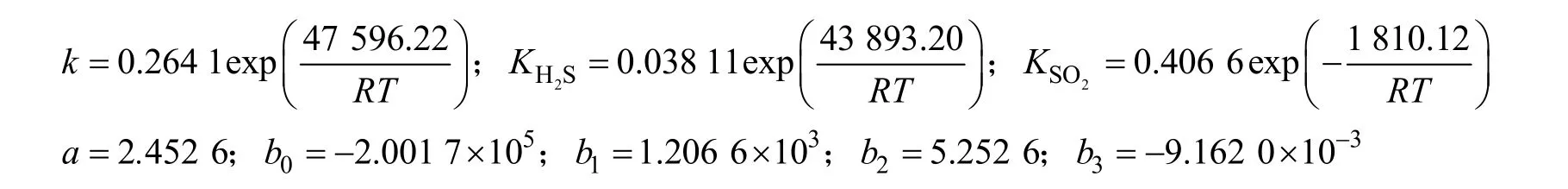
通过对所建立的动力学模型进行统计检验和残差分析，证明所建立的模型是适定的，估值结果是可信的。

[1]Sinha Sourab, Raj Abhijeet, Al Shoaibi Ahmed S., et al.Reaction mechanism form-xylene oxidation in the Claus process by sulfur dioxide [J].The Journal of Physical Chemistry A, 2015, 119(38):9889-9900.

[2]Piéplu A, Saur O, Lavalley J C, et al.Claus catalysis and H2S selective oxidation[J].Catal.Rec.Sci.Eng., 1998, 40(4):409-450.

[3]赵 鹏.Claus硫回收系统的工业化应用研究 [D].天津大学, 2012.

[4]李秉毅.Claus硫回收催化剂研究进展 [J].工业催化, 2016, 24(1):30-33.Li Bingyi.Research progress in Claus sulfur recovery catalysts [J].Industrial Catalysis, 2016, 24(1):30-33.

[5]Karan Kunal, Behie Leo A.CS2Formation in the Claus reaction furnace:  A kinetic study of methane-sulfur and methane-hydrogen sulfide reactions [J].Industrial & Engineering Chemistry Research, 2004, 43(13):3304-3313.

[6]Abdel-Fattah Abdel-Samea, Fateen Seif-Eddeen K., Moustafa Tarek M, et al.Three-dimensional CFD simulation of industrial Claus reactors [J].Chemical Engineering Research and Design, 2016, 112:78-87.

[7]Mendioroz S, Mun˜oz V, Alvarez E, et al.Kinetic study of the Claus reaction at low temperature usingγ-alumina as catalyst [J].Applied Catalysis A: General, 1995, 132(1):111-126.

[8]Karan K, Mehrotra A K, Behie L A.On reaction kinetics for the thermal decomposition of hydrogen sulfide [J].AIChE Journal, 1999,45(2):383-389.

[9]Monnery W D, Hawboldt K A, Pollock A, et al.New experimental data and kinetic rate expression for the Claus reaction [J].Chemical Engineering Science, 2000, 55(21):5141-5148.

[10]Vatani A, Jabbari E, Askarieh M, et al.Kinetic modeling of oxidative coupling of methane over Li/MgO catalyst by genetic algorithm [J].Journal of Natural Gas Science and Engineering, 2014, 20:347-356.

[11]Boekfa B, Pahl E, Gaston N, et al.C-Cl bond activation on Au/Pd bimetallic nanocatalysts studied by density functional theory and genetic algorithm calculations [J].The Journal of Physical Chemistry C, 2014, 118(38):22188-22196.