基于转动惯量的自适应带宽目标跟踪算法

丁业兵

（安徽邮电职业技术学院 通信工程系，安徽 合肥 230031）

基于转动惯量的自适应带宽目标跟踪算法

丁业兵

（安徽邮电职业技术学院 通信工程系，安徽 合肥 230031）

传统均值漂移目标跟踪算法，对跟踪目标的带宽缺乏自动调整，根据物体的转动惯量特性，提出一种自适应带宽算法.该算法采用颜色和边缘特征来表示目标，并用核函数对特征点进行加权生成概率密度分布图，沿着概率密度梯度方向迭代寻找目标中心，而后根据密度分布的转动惯量特征，拟合椭圆，确定长轴、短轴及角度，由长轴、短轴获得目标带宽，从而自适应调整下一帧目标带宽.该算法的跟踪实验结果表明，能够适应目标尺度变化，并抵御同色干扰，估计目标偏转角度.

带宽；转动惯量；均值漂移；目标跟踪；椭圆

1 概述

传统均值漂移目标跟踪算法[1-3]，用物体色彩空间分布来描述目标，具体化为核函数加权的色彩特征概率密度直方图模型，通过巴氏系数来度量候选目标与目标模型的相似性，即沿着概率密度梯度方向迭代收敛到最大峰值稳态点，从而确定候选目标.此算法实时性好，但目标尺度增减自适应算法存在小窗口徘徊和尺度滞后问题[4-5].为了解决传统均值漂移目标跟踪算法的尺度自适应问题，许多研究学者提出了一些改进的算法.如Collins基于Lindeberg尺度空间理论用mean-shift算法迭代寻找目标的位置和尺度[5]，先找到位置再二次迭代找到尺度，运算量较大.彭宁嵩等人利用仿射模型的平移和缩放特性，提取角点，对目标形心进行配准，进而确定轮廓边缘的外接圆半径作为核函数窗口宽度进行更新[6]，提取角点、样本配准的运算大大增加了计算量.左军毅等人充分利用背景和目标颜色的差异对相似度系数进行了修正，以解决小尺度游荡问题[4].还有的论文提出图像分割的方法获得目标轮廓[7]，从而更新目标尺度，但是图像分割或图像配准的方法都大大增加了计算量，同时具有一定的局限性.

目标特征模型的选取，对跟踪性能起着决定性的作用，传统均值漂移目标跟踪算法用颜色来区分目标与背景，特征较为单一，容易受到相同背景色的干扰影响.除了颜色特征以外运用较多的就是纹理特征，一些研究者将局部二值纹理模式特征融入目标表示当中，建立颜色纹理联合直方图[8-9]，此类算法仅适用于具有较多纹理信息的目标.李培华提出对目标颜色进行聚类分析，自适应划分颜色空间[10]，但仍然只是利用了单一的颜色特征.还有些改进思想来源于梯度方向直方图特征[11-12]，对目标的光线变化和部分遮挡具有一定的作用.

仅用色彩来区分目标和背景，容易受到光线变化的影响，也会被相同背景色干扰，所以为了丰富目标信息又不增加过多的计算量，此文采用了边缘加权的方法来减少背景色干扰，增强目标颜色，并引入了物理学中的物体转动惯量特性[13]来解决尺度自适应问题.物体转动惯量的值取决于其形状、质量分布以及转轴位置.文中，将目标特征概率密度分布看作均质椭圆形平面体，形心主轴作为转动轴，通过计算转动惯量来推导椭圆形参数，进而自适应调整目标带宽.

2 Mean Shift算法

Mean Shift是均值偏移的意思，既可以看作是偏移的均值向量[14-15]，也可以看作是迭代的过程.在诸多跟踪算法中，均是以Mean Shift算法为内核，本文也是如此，Mean Shift算法是在一定范围的样本点内指向概率密度梯度方向，连续移动均值向量不断迭代到最终的稳态点的步骤.

假设d维空间中有采样点xi，i=1,…,n，基于核函数K(x)的概率密度函数f(x)为

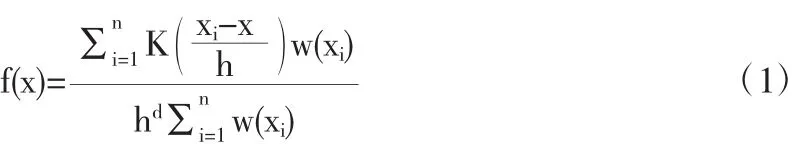
上式中，w(xi)≥0，是采样点xi的权重，K(x)的剖面函数为k(x)，K(x)=k(||x||2)，k(x)的负导数为g(x)，G(x)=g(||x||2)，f(x)的梯度为▽f(x).

其中，Mean Shift向量M(x)为

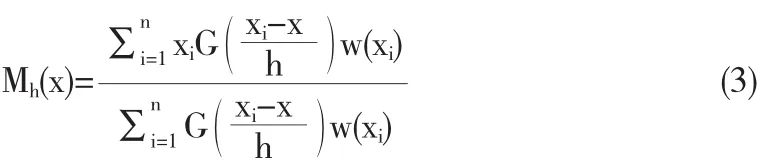
令m(x)为

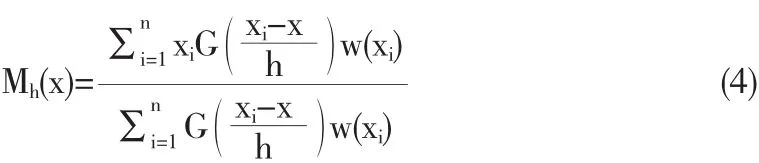
当x=mh(x)时，概率密度达到局部最大.从(2)式可以看出Mean Shift向量指向概率密度增加最大的方向，而且它会沿着梯度方向逐步移动，最后收敛到稳态点.

假设初始点x，核函数G(x)，容忍误差ε，Mean Shift算法迭代步骤如下：

(1)首先计算出mh(x)；

(2)然后，比较mh(x)与x，当||mh(x)-x||＜ε，迭代结束，否则，x=mh(x)，继续执行(1).

3 目标特征表示

每个物体都有各自的特征，对于计算机视频图像而言，目标物体特征的精确定义与提取是区别彼此的关键因素.常见的视频图像物体直观特征有色彩、纹理和边缘，这些特征如何进行提取与统计也很重要.文中采用图像色彩和边缘特征来区别目标与背景，色彩是全局特征，图像所有像素全部参与贡献，而边缘特征则具有局部性，可以描述图像中目标物体和背景的分界以及目标本身的一些边缘纹理.

通过统计颜色空间直方图来表示目标特征，假设目标中心位置为x0，像素位置为{xi}，i=1…n，定义位置xi处的直方图函数b(xi)，b(xi)∈{1…m}，对应像素颜色.选择RGB24格式的色彩模式，红绿蓝三色通道各有8位，可以表征1670万色，为了减少计算量，又不对光照过于敏感，各个色彩通道进行16级量化，即降为16色级，这样，色彩空间量化为4096色.用u来表示量化后的颜色，用凸面单调递减核剖面函数k对像素位置进行加权处理，则颜色u处的概率密度可以表示为

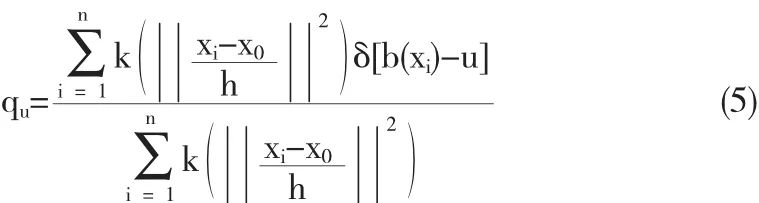
上式中，δ为Kronecker delta函数，其自变量是两个整数，相等为1，反之为0.h为核函数带宽，核函数为

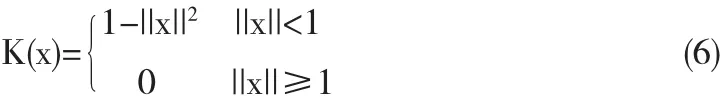
核函数使得像素点距离中心越近权重越高.

统计了基于色彩的概率密度直方图目标模型后，对后续各帧图像进行反向映射投影，创建概率密度分布图.

用颜色直方图来统计色彩特征，具有旋转和尺度不变性，但无法表达边界和纹理信息，所以本文增加了边缘特征，更好的来表征跟踪目标.

将后续彩色图像转换为灰度图像后进行二值边缘检测，这样保留了目标的边界和内部纹理特征，剔除掉同色背景，为了与色彩更好的结合，获取更多的可靠候选目标样本，将色彩概率密度分布进行权重划分，增加边缘色彩权重，降低非边缘色彩权重，再进行归一化处理.

4 转动惯量

平面图形A对平面内X、Y正交轴的转动惯量分别为Ix、Iy，其值分别为

将视频图像中的目标形状看作是均匀质量的椭圆体，图像中的像素位置(x,y)属于图像坐标系，这样可以运用转动惯量的特性来对目标形状进行椭圆拟合[16].

假设图中各像素点大小分别为m1=m2=…=mn=ρ，m=m1+m2+…+mn，椭圆长半轴为a，短半轴为b，椭圆参数方程为x=acosθ，y=bsinθ，θ?[0,2π]，则椭圆体对形心主轴的转动惯量为

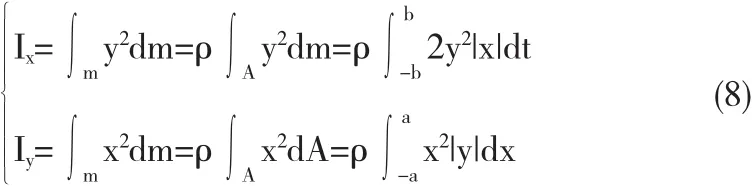
将椭圆参数方程代入上式，可得

通过以上推导，可以求出椭圆长、短半轴大小.

图形的对称轴即是形心主轴，为了获得形心主轴转动惯量，需要对图像坐标系进行平移和旋转.

对于数字图像而言，目标形心坐标(x0，y0)为

图像坐标系原点平移到形心位置后，目标对X、Y轴的转动惯量分别为

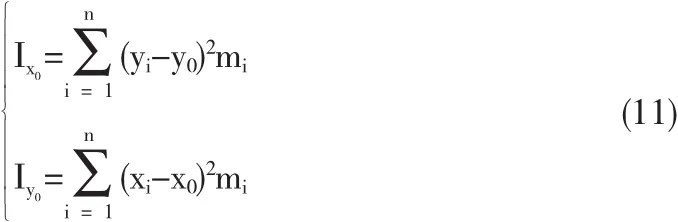
再将平移后的坐标系以形心为原点旋转角度θ后与目标对称轴重合，坐标转换公式为

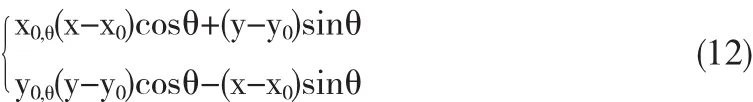
转动惯量、惯量积的转轴公式为

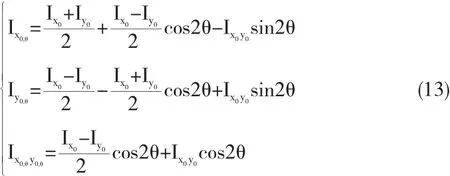
运用形心主轴惯量积等于零的定义，可求得旋转角度θ，即

|2θ|≤π/2，若Ix0＞Iy0，旋转角度θ后，极大值Imax=Ix0,θ；若Ix0＜Iy0，旋转角度θ后，极小值Imin=Ix0,θ，旋转角度θ为正值时，图像坐标系顺时针旋转，旋转角度θ为负值时，图像坐标系逆时针旋转，相对于主轴的转动惯量极大值、极小值分别为

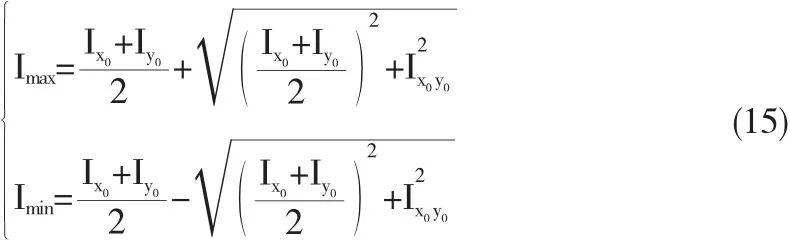
5 基于转动惯量的自适应带宽跟踪算法

目标跟踪首先选定目标模型，提取色彩特征，根据彩色像素的密度和位置来统计直方图，投影创建概率密度分布图，同时结合边缘检测，增加边缘色彩权重来表征目标.

若带宽为h，候选目标像素位置为{xi}，i=1…nh，用Sobel算子对灰度图像进行边缘检测，获得二值图，结果用S(xi)表示，则候选目标概率密度分布图中的像素大小可以表示为

其中，κ为色彩和边缘的权重系数，Pi为各像素位置对应的色彩概率密度，由(5)式，可得

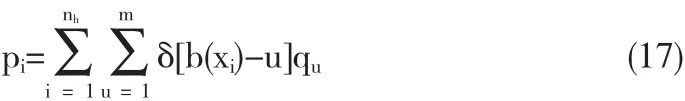
用椭圆来拟合目标概率密度分布的形状，根据上述转动惯量的计算，即可以获得目标的长半轴a、短半轴b以及旋转角度θ.

更新目标尺度，从而自适应调整核函数带宽，当前帧的目标尺度用h(k)表示，h(k-1)为上一帧目标尺度，k为视频图像的帧序号，则下一帧目标尺度为

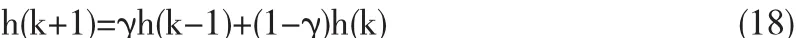
上式中，h(k)为

γ为滤波系数，防止尺度波动多大.

用色彩和边缘来表征目标，基于转动惯量的自适应带宽目标跟踪，过程如图1所示.

图1中，灰色阴影部分是Mean Shift算法，首先确定跟踪目标，初始化跟踪位置和窗口大小，统计色彩直方图，然后对视频图像进行边缘检测，投影创建色彩概率分布图，边缘部分增加权重，通过Mean Shift算法迭代寻找候选目标位置，然后计算候选目标概率分布相对形心主轴的转动惯量，得出椭圆拟合的形状参数，长、短半轴以及旋转角度，最后，由长、短半轴确定下一帧跟踪带宽，并适当扩大计算区域，进入下一帧，对视频序列图像中的目标实现连续跟踪.

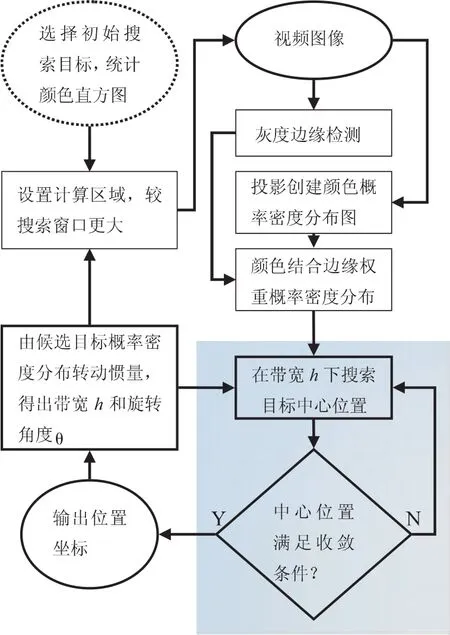
图1 基于转动惯量的自适应带宽跟踪算法流程图

6 结束语

传统Mean Shift目标跟踪算法，带宽自适应存在问题，同时与CAMSHIFT算法一样，仅采用色彩作为目标特征，较为单一.文中提出一种用颜色和边缘纹理来表征目标，并对其概率密度分布采用转动惯量的思想来拟合椭圆，从而自适应调整带宽，并能够估计目标偏转角度的改进CAMSHIFT算法.此算法通过人脸跟踪实验验证，可以抵御同色背景干扰，且能够自适应调整目标带宽和旋转角度.从转动惯量的计算过程，可以看出此算法特别适用于连续均匀分布的概率密度，如人脸等.

〔1〕Comaniciu D,Ramesh V,Meer P.Real-time tracking of non-rigid objects using mean shift[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.SC Hilton Head Island: IEEE,2000:142-149.

〔2〕Comaniciu D,Meer P.Mean shift:a robust approach toward feature space analysis [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(5): 603-619.

〔3〕左军毅,梁彦,赵春晖,等.Mean Shift跟踪算法中尺度自适应策略的研究[J].中国图象图形学报,2008,13(9):1750-1757.

TP391.41

A

1673-260X（2017）05-0012-03

2017-01-10

安徽省高校优秀青年人才基金重点项目(2013SQRL121ZD)