一类具有负系数的广义单叶函数
2017-06-10周海燕李玉毛
何 涛,周海燕,李玉毛
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
数理科学
一类具有负系数的广义单叶函数
何 涛,周海燕,李玉毛
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文引进了一类具有负系数的广义单叶函数,并研究了其系数不等式、偏差、覆盖、闭包定理和极值点.所得结果推广了文[1]中的主要结果.
负系数;广义叶函数;系数不等式;偏差;覆盖;闭包定理;极值点
1 引言
用S(a,k)表示在单位圆盘△={z:|z|<1}内解析函数且单叶函数
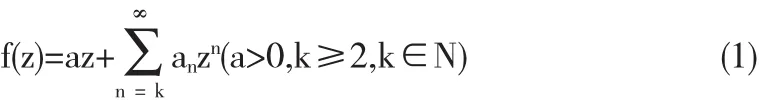
全体组成的类.令T(a,.k)表示S(a,k)中的负系数单叶函数子类:
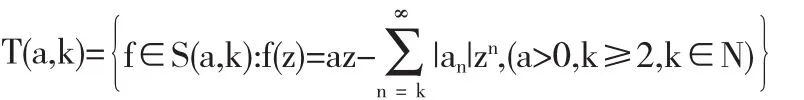
当a=1,k=2时S(1,2)=S和T(1,2)=T为邓琴在文[1]中研究的函数类3.
本文中,作者研究属于T(a,k)类函数的一些属性,得到类中函数的系数,偏差,覆盖,闭包定理和极值点等性质,并推广邓琴在文[1]中的主要结果.
2 主要结果及其证明

证明(必要性) 设f(z)∈T(a,k),下面要证明不等式(2).
由于f'(z)是连续的,并且f'(0)=a>0,由连续函数介值定理可知,存在r1,0<r1<r0,f'(r1)=0,这是矛盾的,因此不等式(2)成立.
(充分性) 由于

所以,对于z1,z2∈△且z1≠z2,我们有
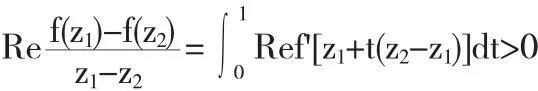
因此,f(z)在△内是单叶函数,即f(z)∈T(a,k).
定理2 设k∈N,k≥2,a>0,如果f∈T(a,k)则极值函数为
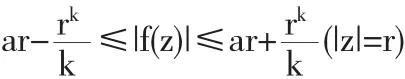
利用定理1,得到
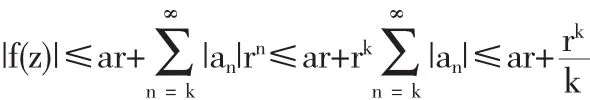
和

定理3 设k∈N,k≥2,a>0,如果f∈T(a,k),则a-r≤|f'(z)|≤a+r(|z|=r)极值函数为
证明 利用定理1,我们得到
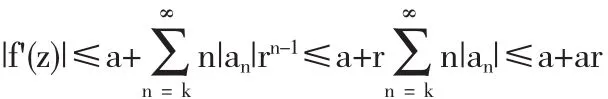
和
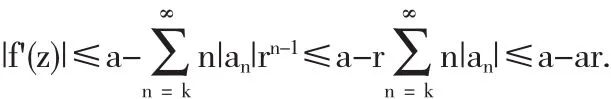
定理4 设k∈N,k≥2,a>0,如果函数

证明 按照f(z)的定义,可得到

从而
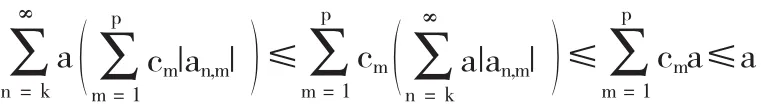
因此h(z)∈T(a,k).
定理5 设
其中λn>0和
证明(充分性) 假设
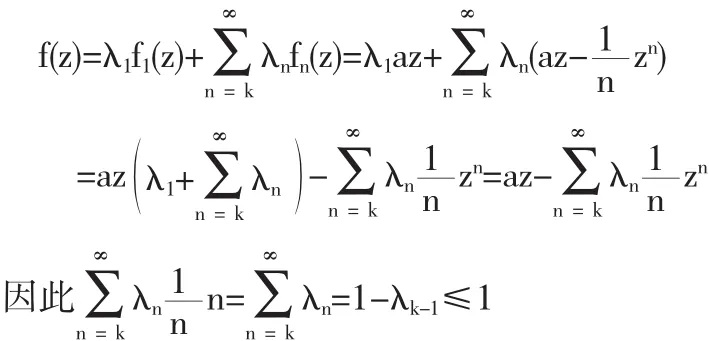
因此,由理论1可知f∈T(a,k).
(必要性) 假设f∈T(a,k),因此
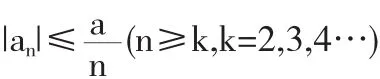
因此

定理6 设k∈N,k≥2,a>0,函数f(z)∈T(a,k),则函数也属于函数类T(a,k).

证明 因为
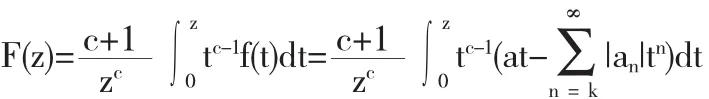

因此,由定理1可得,F(z)∈T(a,k).
定理7 设k∈N,k≥2,a>0,如果F(z)∈T(a,k),则(3)定义的函数,在|z|<R*是单叶的,其中为实数,且c>-1
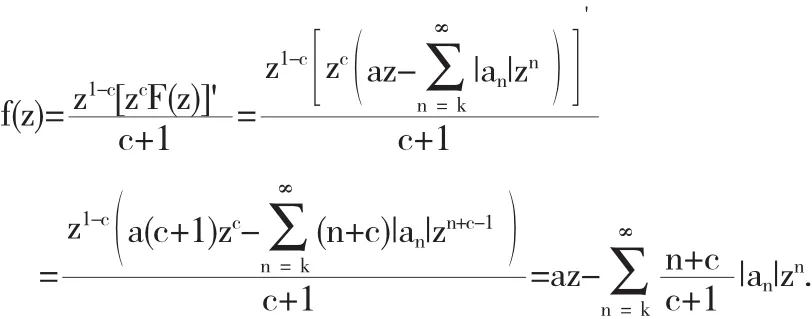
要得到结果,只要在|z|≤R*时,需满足条件|f'(z)-a|≤1或
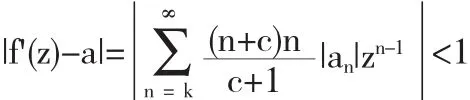
即

则(4)式将成立,上式可化为:
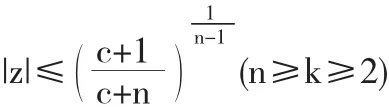
因此,f(z)在|z|≤R*为单叶函数.极值函数为
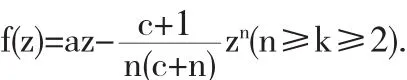
注:当上述定理1至定理7中,分别取a=1,k=2时,就得到文[1]中的主要结果.
〔1〕Qin Deng, On univalent functions with negative coefficients[J].Applied Mathematics and Computation, 2007,189:1675–1682.
〔2〕P.L.Duren.Univalent functions[M].Grundlehren der Mathematischen Wissenschaften,Band 259,Springer-Verlag,New York,Berlin,Heidelberg and Tokyo, 1983.
O174
A
1673-260X(2017)05-0001-02
2017-01-07
