电量相对性

高忠文

摘要：两个不在同一点上电荷之间的相互作用力，在不同参考系中观测值不同的论证基础是电荷之间的相互作用需要传递时间。首先分析一个电荷先产生电场和磁场，电磁场以光速在真空中传递到另一电荷上产生作用力过程的假设基础。指出了根据相对论同时性，得出电荷受力在不同参考系中将发生在不同时间、其力也不会大小相等方向相反、牛顿第三定律不成立结论的问题所在。在此基础上，给出力在不同参考系下保持不变的依据。并根据力在不同参考系下保持不变的条件，结合电荷所受的库仑力及电磁力的情况，给出电量在不同参考系下相对性的表述形式及其论证方法。基于力在不同参考系内保持不变的假设条件，利用类似的推导过程，爱因斯坦的质量相对性的表述公式同样可以被推导出来。

关键词：狭义相对论；电量；力；参考系

DOI：1015938/jjhust201702008

中图分类号： O0412

文献标志码： A

文章编号： 1007-2683（2017）02-0039-05

Abstract：The demonstration foundation， which is used to demonstrate that observed values from the interaction force between two charges， which are not at the same point would be different in different reference frames， is that the transmission of the interaction between charges needs time Firstly， this paper analyzes the foundation of hypothetical process that the electric field and the magnetic field are built by one charge， and then the electromagnetic field would be transferred to another charge in vacuo by the speed of light， and produces force It points out that from the simultaneity of relativity， the force applied to charge would occur in different time in the different reference frames， the force would be neither in the same size nor in the opposite direction， and Newton，s Third Law is not valid longer， the deeper cause of these conclusions would be known On this basis， this paper gives the basis that force would keep invariant in different reference frames， and according to this condition， with the situation of the charge that under the Coulombian force and electromagnetism， the relative form of expression and demonstration methods of electric quantity in different reference frames are given On the basis of the hypothesis that force would keep invariant in different reference frames， with the similar derivation process， the mass relativity equation of Einstein would be obtained

Keywords：electric quantity； special relativity； force； reference frame

0引言

1905年，愛因斯坦在德国的《物理学记事》刊物发表狭义相对论[1]，为现代物理学的发展奠定了基础。在爱因斯坦相对论发表后，人们才真正把运动作为物质存在的方式和物质的形态联系起来。文献[2]认为作用在两个电荷上的力在不同参考系中所指的将不是同一时间。如果假定麦克斯韦方程组服从相对性原理，那么电荷不变原理便可由麦克斯韦方程组推出[2]。泡利（Pauli）在文[3]指出：“因为电子理论符合相对论，因此对于给定电子的运动计算电磁场而言，相对论不会得出以前洛伦兹电子理论所不曾包括的结果”。索末菲（Sommerfeld ）指出：“电荷在所有参考系中都相同，这一点并不是显然的” [4]。文[5]指出：这些理论包含了太多的假设且时间的物理意义不清。 Moon and Spencer 放弃了狭义相对论，而用作用力反作用力相等来解释运动电荷之间的相互作用力，并回到伽利略变换，量子电动力学的未来发展或者某种其它的未来理论也许会有必要回到这一理论[6]。关于电流元之间力的真正本性尚有一些争论。对于完整的回路，作用力和反作用力是大小相等方向相反的，于是人们便不必在过早时期就面临狭义相对论概念的严峻性[2]。我们认为电量是物质的反应，理应与运动关联。就像物体质量与运动关联的关系（不同参考系下物体质量相对性的表述公式一样，电量也与运动关联。下面我们首先论述力在不同参考系下保持不变的依据，然后给出在不同参考系下电量相对性表述形式的推导及论证方法。

1力在不同参考系下保持不变的依据

11力的分类

到牛顿力学创立时，力才被确定为科学概念。力作用在物体上产生的效果是使物体发生形变或改变物体的运动状态，力是使物体产生加速度的原因。

从宏观上看，力可分为两类： 一是物体相互接触而产生的，如摩擦力、拉压力； 二是通过场而发生的，如万有引力、电磁力。从微观上看，物理学归纳出宇宙有四种相互作用力：引力相互作用、电磁力相互作用、强力相互作用、弱力相互作用。后面两种相互作用是基本粒子之间的近距离相互作用。按照狭义相对性原理，这四种力的动力学方程在洛伦兹变换下保持形式不变。

12力在不同参考系下变化的理论及其存在的问题

认为力在不同参考系下变化的学者是这样推导的（详见文献[2]）：如果在一个惯性系中，同时测量作用在两个不在同一点的电荷上的变化着的力，那么，当把这两个力变换到相对于第一个惯性系运动的另一个惯性系中时，作用在两个电荷上的力在新参考系中所指的将不是同一時间。电荷先产生了电场和磁场，电磁场以光速在真空中传播，然后再假定场在其它电荷上产生力的作用。这等价于假定在真空中电磁力本身以光速c传播，不在同一处电荷之间发生相互作用是需要时间的。因而力随时间变化，在参考系Σ1中（Σ1相对参考系Σ0以速度v匀速直线运动），无论t1时刻或者t2时刻，两个力都不会大小相等方向相反，在Σ1中对于两个不在同一处的物体之间的力而言，牛顿第三定律不再成立[2]。电量守恒的假设是当它相对Σ0静止和相对Σ1静止时具有相同的电量。因为如果麦克斯韦方程组在Σ0和Σ1中都成立，电量不依赖于它在Σ0和Σ1中的速度。在此假设基础上，基本粒子电荷守恒原理就可以从麦克斯韦方程组导出。如果这些单个电荷的电量是不变量，那么连续电荷分布的总电量也是不变量[2]。

上面推导利用了相对论中的同时性，初看很有道理。但是仔细思考一下就会发现问题。问题一：假定在真空中电磁力本身以光速c传播，如果按上述所说电磁场是电荷发射的，到达另一个电荷需要有一个传递时间，说明力可以脱离“物体”而存在传递。那么另一个电荷对它也需要一个时间产生作用力。这就像对面放着的两个电风扇，当一个电风扇旋转产生了气流吹到了另一个电风扇对它产生了力，这个力和产生气流的力不是作用力和反作用力，时间也不一样。但不是力变了，力是在传递过程中有了变化。因此有理由把电磁场作用看成是力的传递，而不是直接作用。因为q1发射时刻的受力不是因为q2产生的，而是其产生传递的力。因为其还没有到达q2（这里有很大的隐藏矛盾）所以也谈不上是q1和q2之间的作用力。因而也就无从谈力的变化了（是否相等）。问题二：如果电场是电荷周围原本就存在的（是直接作用的），那么力就没有传递时间的问题了。问题三：从q1看q2是q1先受力，反过来从q2看q1是q2先受力。这就出现了因果矛盾。所以不存在谁发出电磁场到达谁而先产生力的问题。也就是说文献[2]关于力变化的推导存在假设不合理的问题。

上面的分析说明， 文[2]推导所用的时间就存在了问题，所以结论也就值得怀疑。下面我们将论证力在不同参考系下保持不变的观点。

13在不同参考系内力保持不变的论证及思考

谈到力总有两个物体，即施力物体与受力物体，力是不能离开物体而存在的。那么很显然力的效果只与施力物体和受力物体相关，而与观察者无关。即力在不同参考系下保持不变。如果力在Σ1中变为F1，那么在Σ1中受力物体的压力形变、胡克定律等都要变化，将产生一系列矛盾。可见力产生变化最多只是数学意义上的变换，而不是有物理意义。假设力不变，并作为公理是有物理意义及科学根据的。观察下面两个系统，可以理解力不变这一观点。

系统1：

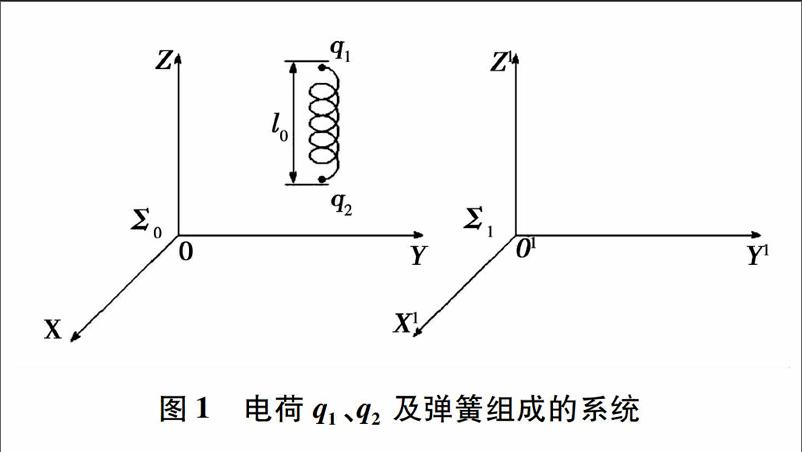
在图1中假设q1、q2带正电，相对Σ0静止。Σ1相对Σ0在Y方向以速度v匀速直线运动，系统处在真空当中。同时假设在两个点电荷q1和q2之间有一个弹簧相连。设其长度为l0。如果假设在Σ1中两个点电荷q1和q2之间的作用力F随着速度v的变化而变化。那么两个点电荷q1和q2之间的弹簧长度l0也将随着作用力F的变化而变化。我们知道在z方向由于没有相对运动，所以也就没有相对论意义上的长度变化[7]。长度变化与爱因斯坦相对论、牛顿力学及遵循胡克定律的弹簧弹力变化都有矛盾。因而在这样的一个观察系统中力是不变的。

系统2 ：

如图2，设Σ1相对于Σ0在Y方向上做匀速v直线运动。物体m0在A点相对于Σ0静止，向下（B点）做自由落体运动。设l0、t0、g0、v∑0分别为在Σ0内观察物体m从A点到B点运动所产生的距离、时间、重力加速度、速度（l在这里即表示A到B的距离变量，也表示长度）。设l1、t1、g1、v∑1分别是在Σ1内观察物体m从A点到B点运动所产生的相对论意义上的观察距离、时间、重力加速度及运动速度。

g0=SX（dvΣ0dt0为在Σ0内观察下落物体的加速度，g1=SX（dvΣ1dt1SX为在Σ1内观察下落物体的加速度。

这说明在相对论观点下，在不同参考系内观察重力是不变的。这为假设力在不同参考系内保持不变提供了又一个证据。它说明力不变假设在这里的逻辑关系是没有矛盾的。在此基础上可以推导出电量在不同参考系下的变换公式。

2电量相对性表述形式的推导及论证方法

21电量相对性论证示意系统

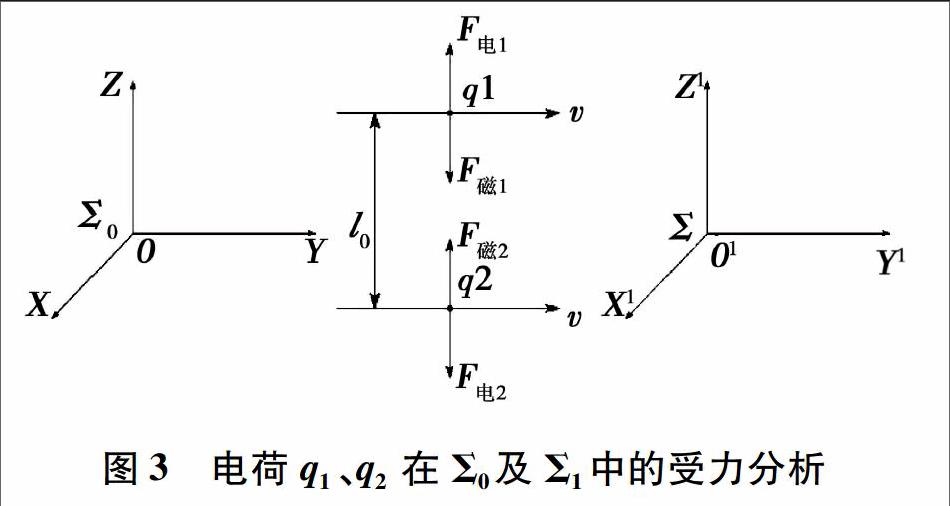
设有两个点电荷q1和q2组成的系统（q1、q2带正电，q1、q2相对Σ0静止，Σ1相对Σ0以速度v沿Y方向运动，系统处在真空当中），见图3。

如果人在相对于q1和q2静止的Σ0参考系中观测q1和q2之间的作用力，则所得到的观察结果是：q1和q2之间只存在电场力。如果在参考系Σ1中观测q1和q2之间的相互作用力，则这时的观测结果为：q1和q2之间存在磁力F磁和库仑力F电1。如果带电体q1和q2的电量在Σ1中没有变化，这时就会有：在Σ1观测q1受力（F电1 -F磁）小于在Σ0观测q1受力F电1了。这样，电荷q1、q2在Σ1参考系中就应由于运动而使其电量值相对Σ0有所变化。

22高斯制下的电、磁力公式表达形式

尽管电荷之间的作用力是波的传递，但是如果我们考虑一种平衡状态或者稳态。而对方也是同样性质的东西，那么它在介质中引起的“波”的效果是一样的，它们之间的稳态作用力是大小相等方向相反的。那么库仑定律，洛伦兹公式，畢奥-萨伐尔-拉普拉斯公式就有了存在的基础。

罗瑟（Rosser）在文[8]中证明了当电流恒定时，毕奥-萨伐尔-拉普拉斯定律便与狭义相对论相一致，但一定要把各个电荷之间的电场力和磁力都包括在内。

在电磁单位制下的毕奥-萨伐尔-拉普拉斯公式为但在高斯制中，由于公式中电流须用静电制电流单位，又根据换算I改写为I/c，因此得出毕奥-萨伐尔-拉普拉斯定律的形式为：

23基于力不变条件的电量相对性公式推导

上面的库仑定律、毕奥-萨伐尔-拉普拉斯定律及洛伦兹力公式中各量是在高斯制下得到的表示形式。我们在图3所示的情况下，根据力在不同参考系内保持不变的条件，可以推出电量q0在以速度v运动的参考系中的观测电量值q。

设q1Σ0、q2Σ0、q1Σ1、q2Σ1分别代表q1和q2在Σ0和Σ1的观测电量，l0、l1分别为q1和q2在Σ0和Σ1中的观测距离。根据力不变条件，针对q1有：

3结论

本文给出了力在不同参考系下保持不变假设的依据，指出了力在不同参考系下产生变化推理基础的问题所在。本文提出的力在不同参考系内保持不变的观点使得“电荷受力在不同参考系中将发生在不同时间、其力也不会大小相等方向相反、牛顿第三定律不成立结论” [2]的矛盾得以解决。同时力在不同参考系内的观测值产生变化，使得胡克定律等受力公式在不同参考系内需要重新解释的问题也不存在。这一观点也符合力是不能离开物体而存在的，力的作用效果只与施力物体和受力物体相关，而与观察者无关的基本属性。本文在上述工作的基础上，给出了电量在不同参考系下相对性的表述形式及其论证方法。在给出这样的推导论证过程中，我们没有涉及实验验证及其它相关问题的全面检验，相关问题有待于进一步的工作。

参 考 文 献：

[1]EINSTEIN A On the Electrodynamics of Moving Bodies[J] Annalender Physik， 1905，16（2）：97-139

[2]W G V罗瑟著 （岳曾元，关德相译）相对论导论[M]（第1版） 北京：科学出版社， 1980： 318-322

[3]Pauli W Theory Of Relativity[M]. London： Pergamon， 1958

[4]Sommerfeld A Electrodynamics[M] New York： Academic Press，1952

[5]张元仲 从牛顿力学到狭义相对论[J]. 力学与实践， 2005， 27（4）： 1-7

[6]Moon P， Spencer D J A new Electrodynamics[J] Franklin Inst， 1954， 257（5）： 369- 382

[7]Einstein A Relativity[M]. Beijing： New word Press， 2014

[8]Rosser W G V Classical Electricity and Magnetism[J] Contemporary Physics， 1961， 38（1）： 321 - 324 （编辑：王萍）