某二维水翼空化数值模型对比研究

蒋文青+郑源+葛新峰

摘要：以二维水翼计算模型为研究对象，采用数值模拟的方法，通过不同的空化模型和湍流模型对计算模型进行数值模拟研究，得到了翼型在空化过程中空泡的运动规律。结果表明：该翼型在不同空化模型下，发生空化时，空化过程包含了空泡的产生、发展、脱落和溃灭几个过程，空化的运动过程总具有明显的周期性；Schnerr-Sauer模型的计算结果与实际的水翼空化流动过程相吻合，Schnerr-Sauer空化模型可以很好地模拟绕水翼的空化流动过程。

关键词：Clark-Y翼型；空化；数值模拟；空泡；运动规律

中图分类号：TK730.2 文献标识码：A 文章编号：1672-1683（2017）03-0204-05

Abstract：We took a two-dimensional hydrofoil calculation model as the research object，and adopted the method of numerical simulation.The movement of the hydrofoil cavity in the cavitation process was obtained through the numerical simulation study on different cavitation models and turbulence models.The result showed：In different types of cavitation models，the cavitation process of this hydrofoil included the generation，development，fall-off，and burst of vacuoles，and the process showed obvious periodicity.The simulation result of S-S cavitation model was consistent with the actual movement.The S-S cavitation model can well simulate the flow around a hydrofoil in the cavitation process.

Key words：Clark-Y hydrofoil；cavitation；numerical simulation；vacuoles；movement pattern

水力机械转轮作为重要的能量转换装置，其叶片断面形状主要为翼型，所以对翼型的研究和设计是提高水力机械性能的主要途径之一。

Huang等[1]应用完全空化模型对某NACA66（MOD）水翼在不同的攻角时的定常空化形态进行了研究。褚学森等[2]应用完全空化模型研究了回转体和圆盘空化器的自然空化流动，给出了不同气核质量分数和湍流参数对空化流动的影响结果。郝宗瑞等[3]针对翼型攻角为8°的二维NACA0015水翼展开了与流体流动特性和流场结构相关的研究。Kang等[4]数值模拟了直径为200 mm的四叶轴流泵的三维空化流动。刘登成等[5]对直径为227 mm的INSEAN E779A四叶模型桨的空化流动进行了研究。张博等[6]为了可以更直观的观察出空化流动的结果，利用实验的方式对绕水翼空化流动展开了研究。张博等[7]应用商用软件CFX的Kubata 空化模型，描述了非定常云状空化形态的发展过程。虽然目前已有较多的使用这些模型来研究非定常空化的文献，但是，由于在一种软件中仅仅会包含一种模型，缺乏对多种模型的对比，特别是对空化流场的结构模拟的对比研究还不是很充分。

本文利用CFD数值模拟方法对翼型的外部绕流形态进行了研究。利用FLUENT[8]对翼型进行不同空化模型以及在不同湍流模型下的空化模拟计算，得到翼型空化的规律。

1 数学模型和计算方法

1.1 空化模型

Schnerr-Sauer 这一空化模型是基于气泡动力学和汽核半径共同得到的，式中的汽核半径RB与体积分数α和汽核数密度 n的关系为RB=α1-α34πn1/3，其中n为给定的经验常数，默认值为n=1×1013。

此空化模型假设空化气泡不相互影响，并且随着蒸汽体积分数的增加，气核密度相应的减小。式中，气核半径RB取值为10-6m，形核位置体积分数αnuc取值为5×10-4，蒸发系数Fvap取为50，冷凝系数Fcond取为0.001。

1.2 湍流模型

湍流的数值模拟方法主要采用了非直接模拟方法中的大涡模拟方法和雷诺平均方法中的RNG k-ε模型。大涡模拟[9-15]方法的基本思想大致上可以概括为：对于大尺寸的涡，采用瞬时的Navier-Stokes方程来直接模拟，并不直接模拟小尺寸的涡，对于小尺寸的涡，则需要通过建立模型考虑其影响。大涡模拟方法对计算机的要求仍然是比较高的，依旧是计算机的内存以及计算速度方面的要求，不过，相比直接数值模拟方法而言，要求是有所降低的，因此，在目前的CFD研究和应用中成为了一个热点。

RNG k-ε模型被称为重整化群，是由Yakhot及Orzag[16]在研究的过程中提出来的。在这一计算模型中，将尺寸比较大的空泡运动的影响，通过修正的方法，从而将黏度的影响体现在小尺寸的空泡上，这样一来就可以将小尺寸的影响效果从整体的运动系统中有效的剔除出去，最终才能够得到了计算需要的k方程和ε方程。RNG k-ε模型在对于修正湍动黏度的过程中，一般需要将平均流动中所产生的漩涡和旋流等流动状况列入考虑的范围；RNG k-ε模型中产生项与流体的流动有一定的相关性，不过在解决问题的过程中还可以看作是空间坐标的函数的问题；RNG k-ε模型的优点在于在面对应变率较高的状态或者流线的弯曲程度很大的情况时，模型的处理效果与实际的發展情况是很接近的。

1.3 计算区域和网格

本文的研究对象选取了Clark-Y翼型，翼型为非对称的结构，该翼型为上弯下平，其中最凸出处为弦长20%处，机翼的厚度为弦长的11.7%，弦长L为0.15m，攻角为零度，整个计算区域见图1，上游来流进口距翼型头部距离为4.5 L，下游去流出口距翼型尾部距离为8 L，两侧壁面距翼型中心各为8 L。在ICEM CFD中将Clark-Y翼型模型导入，对该模型进行网格划分，最终得到适应性强的结构化网格。在翼型的表面处流体的流动并不是很规律的，流动变化较快，因此一般会对翼型的特殊区域进行了网格加密处理，这样一来便可以较为真实的模拟复杂的流动状态。对于重要的区域进行了网格加密，而对于普通的流动区域便可以适当的减少网格的数目，防止网格数太多增加计算的时间和计算量。并且经过网格无关性验证之后，最终确定的网格节点总数为69 969，并确定了壁面附近的y+值为30～60之間，见图2。

图1 计算区域

Fig.1 The computational domain

图2 计算域和网格示意图

Fig.2 Sketch of the computational domain and grids

1.4 边界条件的设置

本文对翼型模型进行空化的数值模拟研究，并通过研究结果对空化模型进行比较和分析。选定入口边界条件为速度入口，假设流动的过程为不可压缩流体流动，选定入口速度为10 m/s，方向为水平方向；出口边界条件设置为压力出口；壁面设置为无滑移壁面剪切条件，即贴在壁面的流体的运动状况与该壁面相同；湍流模型采用与实际情况较为吻合的RNG k-ε模型；进口与回流的湍流边界条件均给定湍流强度与特征尺寸；求解方法采用压力基求解器，SIMPLEC压速耦合算法；选择的多相流模型为和混合物（Mixture）模型，本文描述了多相流动各相之间的相互作用和相互转化情况，具体说来就是在连续的液相流动中贯穿有汽相组分。

2 计算结果与分析

2.1 数值计算结果

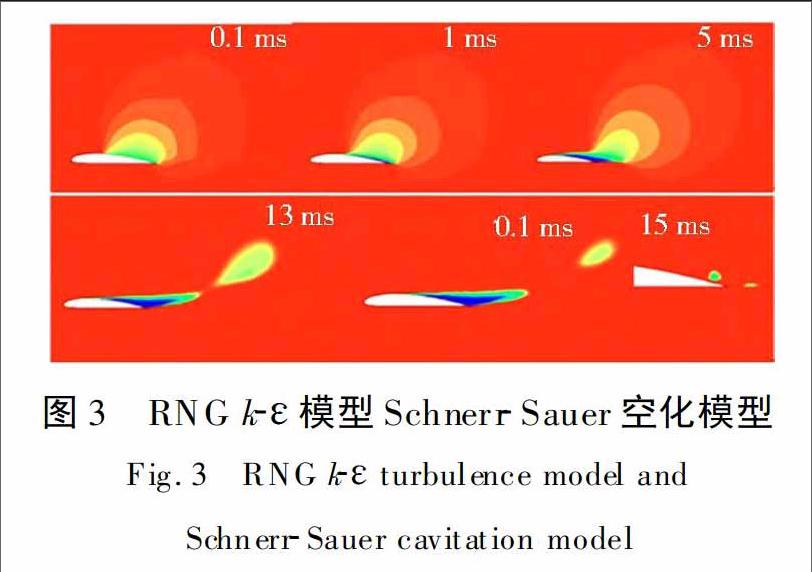
通过本次空化数值模拟，最终得到了在两种不同的空化模型以及湍流模型，不同时间下的空泡体积分数。图3和图4分别表示了在RNG k-ε模型下，图5和图6分别表示了在大涡模拟方法下，不同空化模型以及不同时刻的水蒸气含量随时间变化的分布云图。

在图3所示的Schnerr-Sauer空化模型下，较为明显的出现了气泡的成长、附着、脱落和溃灭的过程。开始时，水翼的前端会产生较为稳定的空化，不过随着时间的发展，从第1 ms开始，空化的气泡在不断长大的过程中也在往翼型的尾部移动，整个过程发生的非常明显，并且因为来流具有一定的合适的速度，所以空泡在第13 ms的时候便开始发生断裂的情况，随着空化的进行，空化气泡便逐渐的缩小，到达了下一个周期的发展与溃灭的过程。在15 ms的时候便进入到了第二个周期的空泡的分离与溃灭的过程。在整个周期中，发生的时间并不是很长，在十几毫秒的时候，整个空化便差不多已经完全了，在这其中空泡的成长占据了较多的时间。

图4所示为在Z-G-B空化模型下的空化结果，与图3中的结果相比较可知，图3中的空化结果较好，无论是成长、分离还是溃灭的过程都比较明显，虽然，图4空泡的数量较多，不过整体的变化过程并不是很好，空泡长大的过程中，生长速度较为缓慢，但附着在翼型表面的空泡较为稳定；空泡并没有一个明显的分离的过程，并且在缩小的过程中空泡的体积分布图有着明显的变化，在接近翼型的尾部处，空泡的体积有一段突变的状态，导致整体的形态不好。从第1 ms开始，便从空化的前端发生了空化，并且前端的空泡越来越多，发生的空化现象很严重，并且会不断地向前方进行扩散，与此同时，在翼型后侧产生的气泡也在不断的向后部移动。从5 ms开始到10.5 ms这段时间内，主要是空泡长大的过程，这一过程在这一时间段内的变化并不是很明显，在10.5 ms到32 ms的时间段内，空泡便在发生溃灭，这一阶段在整个的时间段中占据了很长一部分的时间，不过在溃灭的过程中，附着在翼型的壁面上的空泡体积分数较大的一部分的形状并不是很规整。与Schnerr-Sauer空化模型计算结果相比较而言，Z-G-B空化模型的计算结果显示空化的形态并不是很好，高压区总是附着在翼型的表面，并且持续的时间长，因此空化的结果并不好。

图5 大涡模拟Schnerr-Sauer空化模型

Fig.5 Large eddy simulation of Schnerr-Sauer cavitation model

Schnerr-Sauer空化模型计算得出的结果较好（图5），从产生、成长、飘移到溃灭的过程都是合理的，在翼型的中部往后开始产生空泡，随着时间的发展，附着在翼型表面的空泡的数量越来越多，这也是空化产生的根本原因。于此同时，空泡的产生位置也在开始往后移动。从0.1 ms开始，空泡便在不断地形成过程中，在6 ms到8 ms之间空泡由于来流具有一定的合适的流速，所以空泡有着向后移动的趋势，并且表现的结果较为显著，在6.5 ms到8 ms之间空泡是发生了断裂的过程的，然后在8 ms时刻，空泡在不断的溃灭、缩小，在8 ms到9 ms之间空泡又进入到了一个新的周期的循环之中，不过这一循环与上一循环相比较，整个过程不仅空泡的尺寸减小了，发生空化的时间周期也明显的缩短了，综上所述，在图5中，较完整地展现了出了一个完整的周期以及下一个即将开始的周期，整体来说，应用大涡模拟这一算法对于Schnerr-Sauer空化模型的计算结果还是比较可靠的，计算的结果也比较稳定。图5的计算结果与图3相比较之后可知，两者之间的空化时间是比较有些差距的，之间总共差了大约有5 ms的时间，而空泡在第一阶段发生分离的时间都是在接近空化结束时候发生的，所以，在计算模型发生变化时，空化的时间是有一定的变化的，这一点在以后的研究中需要多加注意。

Z-G-B空化模型的计算结果见图6，虽然产生了较多的空泡，在翼型的表面也附着了较多的气泡，在翼型前端的空泡较为稳定，不过随着时间的发展，附着在翼型表面的气泡并没有向翼型尾部移动。在空化发生之后的溃灭过程中，效果也不是很明显，溃灭的过程中，附着在翼型表面的空泡体积含量不断地增加了。从第1 ms开始，空泡接近翼型的前端的位置开始发生空化现象，在从4 ms开始的时刻，空泡明显的开始向翼型的尾部一侧平移，但并没有发生空泡断裂的状况，可能是由于计算时的速度没有足够的大，使得空化产生的气泡并没有能够与翼型的壁面分离，不过随着时间的发展，附着在翼型表面的空泡的体积分数越来越大。将图6与图4对比之后发现，在大涡模拟的湍流计算方程下，空化发生的时间明显变得更加短了，时间变为了RNG k-ε湍流计算方程计算结果的一半左右，而空化的结果是相似的。

综上所述，在大涡模拟湍流模型的计算结果之下，空化发生的时间明显的缩短了，但是，空化的形态并没有发生太大的改变，整体的空化过程还是一致的，包括了空泡的产生、成长、分离以及溃灭，不过对于Z-G-B空化模型来说，分离和溃灭并不是一个很明显的过程，所以，在空化数值模拟时，选择的空化模型不一致，得到的计算结果从整体上而言是没有太大的差别的。不过需要注意的是，空化的时间周期有了较为明显的缩短，但是相对于整体的时间周期而言，空化发生的相对时间没有太大的变化。

2.2 实验对比

王国玉团队设置的边界条件分别是：10 m/s的速度入口，出口采用的是压力出口，翼型表面采用的是绝热、无滑移固壁条件[7]，与本文的设置相类似。而实验以及数值计算的结果都只是基于修正后的RNG k-ε湍流方程，所以，在本文中就只是将两种空化模型在湍流方程RNG k-ε下的计算结果分别于王国玉团队的实验以及模拟结果进行对比，并分析了产生结果异同的原因。

2.2.1 Schnerr-Sauer空化模型对比

如图7所示，将Schnerr-Sauer空化模型在RNG k-ε湍流模型下计算得到的结果与王国玉团队的绕Clark-y水翼云状空化流动的数值计算与实验对比得到的结果进行比较，计算结果与实验结果的云图相似。在空化发生的时间上也进行了对比，实验中的空化发生时间明显多于数值模拟的时间。由于攻角的原因，空泡产生的位置两者也是有区别的，在实验中，空化气泡从翼型前侧边缘便开始发生空化了，随着时间增加，空泡向翼型尾部迅速移动，脱落现象比较明显。由此可知，攻角的存在会影响空化的起始位置以及空化过程中空泡的脱落程度。

2.2.2 Z-G-B空化模型对比

将Z-G-B空化模型在RNG k-ε湍流模型下的模拟计算结果与绕水翼云状空化流动结构的数值与实验研究得到的结果进行比较，得到的结果差别相对较大。除了上文提到的攻角的影响，使得数值模拟中得到的空泡基本附着在了翼型的中间部位，还有在Z-G-B空化模型下的计算结果即所产生的空化形态与实验中给出的空化形态随时间的变化区别较大，所以，选用的空化模型与王国玉团队的选择可能并不一致，才导致了模拟计算的结果不一致。除此之外，实验中的湍流模型是经过修正的，这样可以改善空化流动过程中的计算精度，并且引入了一种与空化区域水汽相密度相关的系数，对涡黏模型进行了修正。实验的空化过程大约进行了40 ms左右，而数值模拟所经历的时间为30 ms多，时间上两者较接近。综上所述，最终王国玉团队与Z-G-B空化模型的数值模拟方法得到的结果存在一些差距。

3 结论

通过对二维Clark-Y翼型的非稳态空化数值计算，研究得到的成果如下。

（1）选择不同的空化模型和湍流模型，对翼型进行数值模拟计算，得到了翼型在空化过程中空泡的运动规律。分别设置了RNG k-ε和LES两种湍流模型，并在Z-G-B和Schnerr-Sauer两种空化模型下，分别进行数值模拟，最终通过空泡的体积分布云图，得到了翼型在空化过程空泡的运动规律：对于任意的空化模型，水翼空化的非定常过程总是包括空泡的产生、发展、脱落和溃灭几个过程，并且空化的运动过程具有明显的周期性。

（2）提出了Schnerr-Sauer空化模型可以很好地模拟绕水翼的空化流动过程。选取目前较为常用的Z-G-B和Schnerr-Sauer空化模型，在相同的工况下进行空化计算，得出Schnerr-Sauer空化模型的计算结果与王国玉团队的实验研究结果接近，由此可知，对于一般的数值模拟可以直接采用Schnerr-Sauer空化模型。

参考文献（References）：

[1] Huang S，He M，Wang C，et al.Simulation of cavitating flow around a 2-D hydrofoil[J].Journal of Marine Science and Application，2010，9（1）：63-68.

[2] 褚學森，王志，颜开.自然空化流动数值模拟中参数取值影响的研究[J].船舶力学，2007，11（1）：32-39.（CHU Xue-sen，WANG Zhi，YAN Kai.Parametric study on numerical simulation of natural cavitation flow[J].Journal of Ship Mechanics，2007，11（1）：32-39.（in Chinese））

[3] 郝宗瑞，王乐勤，吴大转.水翼非定常空化流场的数值模拟[J].浙江大学学报：工学版，2010，44（5）：1043-1048.（HAO Zong-rui，WANG Le-qin，WU Da-zhuan.Numerical simulation of unsteady cavitating flow on hydrofoil[J].Journal of Zhejiang University （Engineering Science），2010，44（5）：1043-1048.（in Chinese））

[4] Kang C，Yang M G，Wu G Y，et al.Cavitation analysis near blade leading edge of an axial-flow pump[C].International Conference on Measuring Technology and Mechatronics Automation.Los Alamitos：IEEE Computer Society Press，2009：767-770.

[5] 劉登成，洪方文，张志荣等.螺旋桨片状空泡CFD的分析[J].舰船科学技术，2009，24（6）：740-746.（LIU Deng-cheng，HONG Fang-wen，ZHANG Zhi-rong，et al.The CFD analysis of propeller sheet cavitation[J].Ship Science and Technology，2009，24（6）：740-746.（in Chinese））

[6] 张博，王国玉，黄彪，等.绕水翼空化非定常动力特性的时频分析[J].实验流体力学，2009，23（3）：44-49.（ZHANG Bo，WANG Guo-yu，HUANG Biao，et al，Unsteady dynamics of cavitating flows around a hydrofoil[J].Journal of Experiments in Fluid Mechanics，2009，23（3）：44-49.（in Chinese））

[7] 张博，王国玉等.修正的RNG k-ε模型在云状空化流动计算中的应用评价[J].北京理工大学学报，2008，28（12）：1065-1069.（ZHANG Bo，WANG Guo-yu，ZHANG Shu-li，et al.Evaluation of a modified RNG k-ε model for computations of cloud cavitating flows[J].Transactions of Beijing Institute of Technology，2008，28（12）：1065-1069.（in Chinese））

[8] 江帆，黄鹏.Fluent高级应用与实例分析[M].北京：清华大学出版社，2010.（JIANG Fan，HUANG Peng.Fluent：advanced application and case analysis[M].Beijing：Tsinghua University Press.（in Chinese））

[9] Feiz A A，Ould-Rouis M，Lauriat G.Large eddy simulation of turbulent flow in a rotating pipe[J].International Journal of Heat and Fluid Flow，2003，24（3）：412-420.

[10] Mary I，Sagaut P.Large eddy simulation of flow around an airfoil near stall[J].AIAA Journal，2002，40（6）：1139-1145.

[11] Grigoriadis D G E，Bartzis J G，Goulas A.Efficient treatment of complex geometries for large eddy simulations of turbulent flow[J].Computers and Fluids，2004，3（2）：201-222.

[12] Shen L，Yue D K P.Large-eddy simulation of free-surface turbulence[J].Journal of Fluid Mechanics，2001，440：75-116.

[13] Julian R E，Smolarkiewiez K.Eddy resolving simulations of turbulent solar convection[J].International Journal for Numerical Methods in Fluids，2002，39（9）：855-864.

[14] Li J C.Large eddy simulation of complex turbulent flows：physical aspects and research trends[J].Acta Mechanica Sinica，2001，17 （4）：289-301.

[15] Sotiropoulos F.Progress in modeling 3D shear flows using RANS equations and advanced turbulence models[J].Calculation of Complex Turbulent Flows，WIT Press，2001，31-53.

[16] 王福军.计算流体动力学分析-CFD软件原理与应用[M].北京：清华大学出版社，2004.（WANG Fu-jun.Computational fluid dynamics analysis：CFD software principles and applications[M].Beijing：Tsinghua University Press，2004.（in Chinese））