贝叶斯神经网络在城市短期用水预测中的应用
2017-06-09占敏薛惠锋王海宁万毅
占敏+薛惠锋+王海宁+万毅


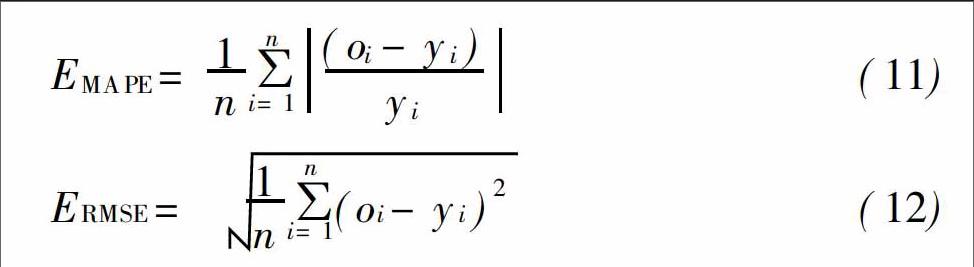
摘要:严格水资源管理制度实施的背景下,短期用水量预测对城市供水系统调度的作用日益显著。在分析日用水量时序演化规律及随机性影响因素的基础上,以前7天每日用水量、日最高温度、当月用水量占全年比、日降水量、节假情况作为短期用水量预测指标,构建了BP神经网络城市短期用水量预测模型,并利用贝叶斯正则化对BP神经网络进行优化。将两种模型应用于广州市某自来水公司进行对比验证,结果表明,贝叶斯神经网络预测模型与BP神经网络预测模型的平均绝对百分比误差分别达0.87%与1.85%,经贝叶斯正则化的BP神经网络模型泛化能力更强,精度提高了约0.98%,更符合城市短期用水量预测的高精度要求。
关键词:短期用水量;神经网络;贝叶斯正则化;预测模型
中图分类号:TV213 文献标识码:A 文章编号:1672-1683(2017)03-0073-07
Abstract:Under the background of implementation of the most stringent management regulations on water resources,the prediction of short-term water consumption is playing an increasingly significant role in urban water supply system scheduling.Based on the analysis of the temporal evolution pattern and random factors of short-term water consumption,a Bayesian neural network prediction model for urban short-term water consumption was built with the daily maximum temperature,daily water consumption of the previous 7 days,ratio of water consumption of the current month to the annual amount,daily precipitation,and holidays as predictors of short-term water consumption.Meanwhile,Bayesian regularization was used to optimize BP neural network.Both BP network model and the optimized model were applied to a running-water company in Guangzhou City for tesing.The results indicated that the mean absolute percentage error of the Bayesian neural network prediction model was 0.87%,while that of the BP neural network prediction model was 1.85%.Compared to the BP neural network prediction model,the optimized model has stronger generalization ability,with accuracy improved by about 0.98%.Thus,it fits better with the high-precision requirement of urban short-term water prediction.
Key words:short-term water consumption;neural network;Bayesian regularization;prediction model
水资源是保障区域发展和人民生活基础性资源与战略性资源,然而我国近2/3的城市呈“缺水”或“严重缺水”状态,多地已逼近用水总量红线。在最严格水资源管理制度[1]实施的背景下,日益突出的水资源供需平衡矛盾给城市供水调度带来了空前的挑战。长期用水总量红线目标需要短期用水实时控制与调节来实现,且短期用水量预测作为城市供水系统运行工况模拟与调度决策基础和前提,是城市供水调度关键的一环,本文试图建立高精度的逐日用水量预测模型,以提高供水系统工况模拟的合理性及调度决策的可靠性,支撑城市供水系统的稳定运行,促进区域水资源的高效利用与节约。
每日用水量会随着时间与天气等条件的影响而发生变化,具有复杂性、非线性、时变性等特点。目前,较为常用的用水量预测方法有灰色预测法、回归预测法、时间序列预测法与神经网络预测等[2-3]。其中,灰色预测法与时间序列预测法只是对历史数据的挖掘,在处理随机性因素造成的用水变化异常情况时预测效果受限。回归预测考虑了用水量的影响因素,但该方法中因素的选择对模型的精度影响较大。神经网络具有较强的自组织、自学习及归纳与容错能力[4-5],且对非线性问题拟合效果较好,因此,本文采用经典的BP神经网络算法进行预测[6-7]。针对上述方法无法兼顾日用水量时序规律与影响因素造成异常变化的情况,本文将历史数据及影响因素同时纳入预测指标体系中,在考虑日用水量的周期性、趋势性及随机性情况下进行预测;针对BP神经网络推广能力不足等问题,采用贝叶斯正则化对网络进行改进并实验验证。
1 城市短期用水量预测模型构建
1.1 BP神经网络
人工神经网络由多个神经元组成,各个神经元之间相互连接[8]。网络结构一般分3层:1个输入层、1个输出层及连接二者的若干个隐含层。BP神经网络(Back-propagation Network)是目前應用最为广泛的神经网络之一,当网络的隐含层为1时,结构图见图1。网络工作机理是:信息进入网络的输入层后传播至隐含层,再利用隐含层各神经元的激活函数进行运算并将结果传播到输出层[9]。隐含层的层数视实际问题的复杂度而定。一般而言,一个隐含层即能逼近任何非线性连续函数。
BP神经网络的特点是将前一次输出结果的误差反向传播来重新调整其权值及阈值,当误差达到最小或极小的时候结束[10]。因此BP神经网络多了一个向后传播过程。网络在向前传播时运算方式如下:
1.2 贝叶斯神经网络
泛化能力是衡量神经网络结构性能的重要标志,一个神经网络模型可能对训练样本集会达到较好的匹配效果,但是当训练好的网络去处理一些未知的信息的误差可能会非常大。这是由于网络过度依赖训练样本,当训练样本不能完全描述全样本的特征时,网络便不能得出其内在规律,导致其不能很好地对未知信息进行准确判断,推广能力不足[12]。根据Moody原则,过拟合现象是由于网络结构冗余而造成的,在样本出现较小误差时,可能会因冗余度过高而输出误差较大的结果。正则化方法是在目标函数(3)式中增加一个正则化项或惩罚项[13],实现目标的结构风险最小化。因此,目标函数被调整为
新的性能指标函数能在当网络训练误差尽可能小的情况下,得到较小的权值[14]。这相当于在保证网络满足拟合精度要求情况下减少其网络节点,降低其复杂度,提高其泛化性能[15]。
贝叶斯神经网络就是对神经网络的权值向量赋一个先验分布,若在样本較少时,可利用该先验分布防止网络出现过拟合。随着样本的增加,在训练过程中,贝叶斯神经网络不断地自动调整正则化系数,提高网络的泛化能力,并能自动调整重要的输入变量权值的后验分布使其达到概率最大化,其预测精度就可能会有所提高,增强其泛化能力[16]。
贝叶斯方法的核心是以先验知识和数据对模型加以评价,该方法将未知变量θ看成一个具有不确定性的随机变量,θ的不确定性可以用概率或概率分布进行描述。在没有获得数据时,对一个变量的未知情况的概率分布进行表述称为先验分布。贝叶斯公式可表示为
式中:γ是神经网络的有效参数的个数,γ=m-2βtr(H)-1,γ∈(0,m),m是神经网络参数的总数,H即目标函数的Hessian矩阵。但式中的Hessian矩阵的计算量较大,本文采用GAUSS-NEWTON法近似计算Hessian矩阵[17]。具体公式为H=2αJT+2βIm,其中J是训练误差的Jacobi矩阵。α与β的具体计算步骤如下:(1)初始化α、β与神经网络连接权值;(2)将误差反向传递,权值用最速下降法调整从而减少代价函数E;(3)计算有效权值数γ;(4)重新对α、β进行计算;(5)重复步骤(1)至(3),直到满足要求。
贝叶斯神经网络能在网络训练时自适应地调整α、β的值,最终得到最优解,而一般的正则化方法却很难做到[18]。贝叶斯正则化在神经网络训练中选定α与β的值,把网络权值作为随机变量处理,并设训练数据集与权集的先验概率服从高斯分布,然后按贝叶斯规则,根据后验概率的最大化求出目标函数E最小点处W的d与β。
1.3 基于贝叶斯神经网络的城市短期用水量预测模型 城市用水量一般包括生活用水、工业用水及公共用水。对于城市日用水量而言,一定程度上受温度、降水量、季度、节假情况等因素的影响。
(1)温度变化会导致用水量的不同。在温度较高条件下,居民生活方式可能发生改变,生活用水量呈上升趋势;维持工业机械正常运作比平时需要更多的水量进行降温处理,工业用水增加,且日用水量的增幅与温度的变化率密切相关。
(2)降水量在一定程度上可以弥补城市需水量,如降水量的大小会直接影响到公共用水量,当公共绿地或公共建筑需补水时,若降水量较多,则人工补水量减少;反之,人工补水量增大。
(3)在节假日,居民在家时间相比工作日更长,居民生活用水将会大量增加,同时部分企业可能作业量减少甚至停工,造成工业用水下降。若无法定假日,一周内用水量近似为周期性变化。
(4)在不同的季度,居民生活条件及方式和企业的生产条件与市场需求都会有不同程度的变化,导致用水量发生改变,该变化可近似为以12个月为周期的周期性变化。
综上所述,日用水量可能存在以每日为单位的周内的短周期性和以季度为单位的年内的长周期变化;而温度、湿度及节假情况又会增加日用水量的随机性,再考虑日用水量可能存在的趋势性变化。因此,本文遵循指标建立的科学性、完备性、实用性、可操作性、独立性的原则,结合上述日用水量的周期性、随机性及趋势性,选取前7天的用水量、日最高温度、日降水量、当月用水占全年比、节假情况这11个指标作为网络的输入节点,以当天的用水量为输出结果建立短期用水量预测模型。即:
式中:Dn-k为第(n-k)天的用水量(k=0,1,2,3,4,5,6,7);Tn为第n天的最高温度;Qn为判断第n天是否为节假情况,若是工作日,则Qn=0,若是双休日,则为Qn=1,若是其他法定假日,则Qn=2;Rn为根据天气预报获取的第n天的预降水量;Sn是第n天所在的月份历史年份占全年用水量的百分比。
将网络的隐含层设为一层,根据Kolmgrov定理,网络隐含层神经元的数目为网络输入数目的2倍加1,即隐含层神经元个数取为23,构成一个11-23-1的神经网络模型。该模型可提前预测后一天的用水量。
前述提到神经网络的泛化能力是网络性能的一个重要标志,若网络泛化能力低,则即使网络对于训练样本拟合度较高,网络对未知样本的预测精度也可能较低。而网络的泛化能力的主要影响因素就是网络结构的复杂度,日用水量11-23-1的神经网络预测模型,网络输入层及隐含层节点较多,复杂度较高,若利用BP神经网络进行预测,则其对训练样本能得到较好的拟合效果,但是若样本出现较小的误差,则可能会因网络冗余度较高而引起网络输出的极大偏差,实际样本不可避免存在噪声点,因此BP神经网络预测的推广能力难以保证。贝叶斯神经网络不仅考虑网络对历史日用水量的拟合度,而且还尽可能根据贝叶斯正则化自动调整网络参数,使得一些冗余的网络结构对应的权值最终趋向于0,这就自动减小网络的复杂度,减少因样本失真而导致的预测精度大幅下降的问题,增强了网络的泛化能力。
2 实证分析
本文以国家水资源监控能力建设项目监测的广州市某自来水公司为例,利用国家水资源管理信息系统中该公司2015年9月24日至2016年1月3日实时监测上报的日用水量数据,结合广州市2015年10月1日至2016年1月3日的天气数据,分别构建BP神经网络与贝叶斯正则化后的城市短期用水量预测模型。
由于样本有限,该公司各月用水量占比用广州市各月用水量占比替代,按近五年广州市各月用水占比计算得出。广州市1月、12月用水占全年的7.5%左右,2月份占7%,3月、4月、11月份为8%,5月、6月、10月为8.5%,7月份为9.5%,8月份达到最高10%,9月份为9%。将收集的95个样本的前80个样本作为网络的训练集,最后15个样本作为网络的测试集以检验模型性能。利用MTALAB实现两种神经网络算法,设网络的学习函数为tansig函数,最大训练次数设为600,训练的目标误差为0.005,其余参数取默认值。模型训练前对数据进行归一化处理。根据tansig的曲线特性,将归一化函数设为x*=2x-xminxmax-xmin-1,在得出结果后再反归一化得出预测的日用水量。本文采用平均绝对百分比误差MAPE(Mean Absolute Percentage Error)与均方根误差RMSE(Root Mean Square Error)对两种模型的预测效果进行评价:
将2015年12月20日至2016年1月3日的数据分别在BP神经网络于贝叶斯神经网络预测模型中运行,对测试样本的拟合度见图2和图3,预测的相对误差曲线如图4,表1为模型预测的日用水量与日监测用水量的比较,表2为预测模型的性能对比表3与表4分别为两种模型训练后权值对比。表3与表4中的Input表示输入层神经元,Hidden表示输出层神经元(以输入层神经元至隐含层第1个神经元至第5个神经元的权值为例)。
本的拟合度为0.995 76,而BP神经网络对样本的拟合度为0.997 32。但是,图4、表1与表2显示,BP神经网络短期用水量预测模型的最大相对误差为5.76%,最小相对误差为0.34%,误差波动幅度较大,而贝叶斯神经网络预测模型则相应为2.89%与0.31%;传统BP神经网络预测模型的均方误差为20 580 m3,而贝叶斯神经网络预测模型则为9 106 m3,表明贝叶斯正则化后的神经网络具有更高的稳定性。另外,BP神经网络预测模型的平均绝对百分比误差为1.85%,而贝叶斯神经网络预测模型则为0.87%,其精度提高了0.98%。
由表3及表4可知,BP神经网络对样本训练后其输入层到隐含层前5个神经元的连接权值取值区间为(0.0100,1.0000),而贝叶斯神经网络中的连接权值中有15个连接权值为0.000 1或-0.000 1,由于网络的连接权值是有随机函数随机分配的浮点数,无法取整数0,取±0.000 1相当于0,这表明经贝叶斯正则化后的神经网络能自动去除输入变量之间的冗余,减小网络的复杂度。
综合上述结果可知,贝叶斯正则化能在网络拟合精度与复杂度之间自动调节,使得网络能在保证对训练样本拟合精度的基础上调整网络参数,减小网络的复杂度,增强网络的泛化能力,提高网络对未知事物的预测精度。
3 结论
本文构建的日水量预测指标体系,在分别采用贝叶斯神经网络与BP神经网络算法进行实验验证时,其预测值绝对百分比误差分别为0.87%与1.85%,说明了指标选取的有效性;在两種模型训练后的拟合度及连接权值对比时表明贝叶斯正则化能在满足对训练样本的拟合精度的条件下去除网络结构的冗余,降低网络复杂度;神经网络贝叶斯神经网络模型的精度比BP神经网络模型的精度高0.98%,证明了贝叶斯正则化方法能有效提高网络的泛化能力,该模型可为城市供水系统的日用水量预测提供参考,为供水系统调度提供准确的数据支撑,促进城市水资源的节约与合理利用。
参考文献(References):
[1] 孙雪涛.贯彻落实中央一号文件实行最严格水资源管理制度[J].中国水利,2011 (6):33-34,52.(SUN Xue-tao.Implement No.1 Central Document and carry out strictest regulations on water resources [J].China Water Resources,2011(6):33-34,52.(in Chinese))DOI:10.3969/j.issn.1000-1123.2011.06.017
[2] 何忠华.城市需水量的预测研究[D].合肥:安徽理工大学,2009.(HE Zhong-hua.The research for forecasting urban water demand [D].Hefei:Anhui University of Science and Technology,2009.(in Chinese))DOI:10.7666/d.y1575148
[3] 展金岩.深圳市水资源供需预测及可持续利用研究[D].北京:华北电力大学,2012. (ZHAN Jin-yan.Supply and demand prediction and sustainable utilization of water resources in Shenzhen [D].Beijing:North China Electric Power University,2012.(in Chinese))DOI:10.7666/d.y2140293
[4] 颜端武.面向知识服务的智能推荐系统研究[D].南京:南京理工大学,2007.(YAN Duan-wu.Research on knowledge service oriented intelligent recommendation system [D].Nanjing:Nanjing University of Science and Technology,2007.(in Chinese))DOI:10.7666/d.y1154967
[5] 陈佳.基于粗糙集理论和人工神经网络的滚动轴承故障诊断[D].成都:西南交通大学,2012.(CHEN Jia.Rolling bearing fault diagnosis based on rough set theory and artificial neural network [D].Chengdu:Southwest Jiaotong University,2012.(in Chinese))DOI:10.7666/d.y2108628
[6] Maidment D,Pazren E.Time patterns of water use in six Texas cities [J].Journal of Water Resources Planning and Management,ASCE,1984,110(1):90-106.
[7] Maidment D,Miaou S,Crawford M.Transfer function models of daily urban water use [J].Water Resources Research,1985,21(4):425-432.
[8] 郑忠.适应性组合分类器遥感分类研究[D].长沙:中南大学,2013.(ZHENG Zhong.Remote sensing classification by adaptive combing multiple classifiers [D].Changsha:Central South University,2013.(in Chinese))DOI:10.7666/d.y2423974
[9] 王志勇,陈昊鹏.基于组合神经网络模型的函数逼近方法[J].计算机应用与软件,2008,25(7):137-139.(WANG Zhi-yong,CHEN Hao-peng.Function approximation based on combined neural network model [J].Computer Applications and Software,2008,25(7):137-139.(in Chinese))DOI:10.3969/j.issn.1000-386X.2008.07.055
[10] 李蓉.神经网络在缺陷接地结构最优化设计中的应用研究[D].天津:天津大学,2007.(LI Rong.Study of the application of neural networks to optimization design of defected ground structures [D].Tianjin:Tianjin University,2007.(in Chinese))DOI:10.7666/d.y1358087
[11] 雷成华,刘刚,李钦豪.BP神经网络模型用于单芯电缆导体温度的动态计算[J].高电压技术,2011,37(1):184-189.(LEI Cheng-hua,LIU Gang,LI Qin-hao.Dynamic calculation of conductor temperature of single-cable using BP neural network [J].High Voltage Engineering,2011,37(1):184-189.(in Chinese))
[12] 郝圣桥.液压AGC伺服阀在线故障智能诊断的研究[D].上海:上海交通大学,2010.(HAO Sheng-qiao.On-line intelligent fault diagnosis of hydraulic AGC servo valve [D].Shanghai:Jiaotong University,2010.(in Chinese))
[13] 王智文.贝叶斯神经网络与FTIR技术在多气体定量分析中的应用研究[D].太原:中北大学,2011.(WANG Zhi-wen.Research on the application of Bayes neural network and FTIR in quantitative analysis of multi-gases [D].Taiyuan:North University of China,2011.(in Chinese))
[14] 方彩婷.基于BP神经网络的图像识别与跟踪研究[D].西安:西安电子科技大学,2006.(FANG Cai-ting.Study of image recognition and tracking based on BP neural network [D].Xi′an:Xidian University,2006.(in Chinese))DOI:10.7666/d.y858729
[15] 张雨浓,陈俊维,刘锦荣,等.基于权值与结构确定法的单极Sigmoid神经网络分类器 [J].计算机应用,2013,33(3):766-770,809.(ZHANG Yu-nong,CHEN Jun-wei,LIU Jin-rong,et al.Unipolar sigmoid neural network classifier based on weights and structure determination method [J].Journal of Computer Applications,2013,33(3):766-770,809.(in Chinese))DOI:10.3724/SP.J.1087.2013.00766
[16] 束志恒.化学化工数据挖掘技术的研究[D].杭州:浙江大学,2005.(SHU Zhi-heng.Research on the data mining in chemistry and chemical engineering [D].Hangzhou:Zhejiang University,2005.(in Chinese))
[17] 李辉.提高密度泛函理论方法计算吸收能的精度:神经网络和遗传算法[D].长春:东北师范大学,2009.(LI Hui.Improving the accuracy of density-functional theory calculation for absorption energies:neural network and genetic algorithm [D].Changchun:Northeast Normal University,2009.(in Chinese))
[18] 田志偉.贝叶斯神经网络在股票预测中的应用[D].无锡:江南大学,2011.(TIAN Zhi-wei.Application of Bayesian neural network on stock forecasting [D].Wuxi:Jiangnan University,2011.(in Chinese))
