考虑再生循环的多杂质用水网络全局优化

陈晓露，常承林，王彧斐，冯霄



考虑再生循环的多杂质用水网络全局优化

陈晓露1，常承林2，王彧斐1，冯霄2

（1中国石油大学(北京)化学工程学院，北京 102249；2中国石油大学(北京)新能源研究院，北京 102249）

引入再生循环单元可以有效地减少多杂质用水系统整体的新鲜水消耗量和废水排放量。其现有的数学规划模型是一个非凸性严重的混合整数非线性规划问题，直接求解不仅计算难度大而且求解速度慢，这样只能得到局部最优解。本文利用分段线性松弛的方法对该模型进行处理，将双线性等式约束转换成线性约束，从而使复杂的水网络模型转换为对应的混合整数线性规划问题，因现有的商业优化软件对混合整数线性规划问题的求解算法已经非常成熟，这样降低了计算难度并取得全局最优解。算例结果表明分段线性松弛的方法可以使求解简单，能够获得全局最优解。管线费用的减少使年度化费用降低，全局优化能得到一个经济性更好的多杂质水网络，这种方法对于节省设备投资和操作费用，具有重要意义。

多杂质用水网络；数学规划模型；分段线性松弛；全局优化

21世纪以来，全球水资源匮乏情况愈发严重，世界各国越来越注重水资源的节约利用和循环利用。在石化行业中，废水必须经过废水处理单元脱除杂质，达到一定排放标准后，方可排放到环境中。在用水单元和污水处理单元之间进行的废水直接回用、再生回用和再生循环，能够从整体上减少新鲜水的耗量。自20世纪90年代以来，多杂质用水网络的优化一直是业内学术研究的焦点。相关学者提出了大量研究设计方法，主要包括图示法和数学规划法。

图示法是一种以用水单元的性质为基础对其不同用水需求进行分析的启发式方法。其中用水单元的关键性质主要包括进出口杂质浓度上限和对水的流量要求。20世纪90年代初，TAKAMA等[1]通过对工业用水过程进行研究，提出了用水网络优化设计的相关概念。WANG和SMITH[2]提出水夹点的设计方法。该方法通过假定各种杂质浓度转移的线性关系来设计最优的用水网络。FOO[3]分析了水夹点技术，并指出图示法具有物理概念明确、方便理解、直观简洁等优点。但是，该方法设计的拓扑结构往往很难达到最优，特别是当用水单元数量较多时，网络结构中往往存在大量的回路。针对这一缺陷，ZHENG等[4]通过设置一个或多个内部中间水道，建立了用水网络设计的新方法。KUO和SMITH[5]研究了带有再生回用和再生循环单元的用水网络，进而提出整体上的设计方法以获取最优的用水方案。BAI等[6]通过图解法对单杂质的再生回用水网络的优化问题进行研究。TAN等[7]通过分析水夹点技术的特点，对含有再生单元的用水网络设计方法进行了改进。NG等[8]提出可以自动确定新鲜水目标值的代数方法。在此基础上，DENG和FENG[9]开发出设计用水网络的改进问题方法，以增大水的最大重复利用率。

以上关于用水网络设计的图示法，比较适合对于单杂质水系统的研究。但在实际生产中所涉及的大多是包含多种杂质的污水，图示法对于这类复杂问题不能很好地处理。而另一方面，数学规划法能够考虑多杂质用水网络设计的方法。由于具有更加全面、灵活和准确等优势，许多研究学者把这种方法广泛地应用于工业用水网络设计的学术研究和工业案例中。

DOYLE和SMITH[10]在研究多杂质用水系统的设计问题时，提出了简化的数学模型。该模型假设杂质的负荷与进出口浓度之差成线性关系，将用水网络的优化设计表述为一个混合整数非线性规划问题。LIU等[11]提出一种数学规划模型来确定化工厂最优用水量的方法并对水处理网络进行了分析和研究。FENG等[12]使用数学规划法，建立了针对再生循环用水网络设计的超结构模型。FARIA等[13]对用水网络模型进行改进，并讨论了水的预处理、操作费用和零排放等问题。BAI等[14]通过分析杂质浓度和负荷的关系曲线，建立了相应的数学模型来优化具有再生回用单元的的用水网络。以上这些关于用水网络设计的数学模型大部分是非凸性严重的混合整数非线性规划问题（MINLP），直接求解容易得到局部最优解。针对求解困难的问题，BERGAMINI等[15]利用改进的外逼近方法处理用水网络设计的数学模型，从而获取较好的改进解。KARUPPIAH和GROSSMANN[16]对用水网络数学模型中的双线性项约束进行处理，求取最小的新鲜用水流量，但该模型没有考虑管线费用。YANG 等[17]利用线性松弛技术对带有污水处理装置的用水网络进行求解。由于该方法没有对双线性项进行分段处理，因而只能求得局部最优解。

由于多杂质用水网络的数学模型中存在很多双线性等式约束和非线性的目标函数[18]，现有的商业求解器只能求得局部最优解，甚至对大规模问题得不到良好的可行解[19]。针对这一问题，本文作者利用分段线性松弛方法对多杂质用水网络数学模型中的双线性约束和非线性目标函数进行处理，使复杂的MINLP模型转换为对应的混合整数线性规划问题（MILP）问题。与直接求解方法相比，分段线性松弛方法降低了计算的难度，从而可以在用水网络的设计问题中获取全局最优解。

1 数学模型

图1为KARUPPIAH和GROSSMANN[16]提出的水网络超结构，可以看出该超结构包含一系列用水单元和若干个污染处理单元。在该图中，PU表示用水单元，TU表示污水处理单元，M表示虚拟混合器，S表示虚拟分流器。它包含各个用水单元以及再生单元之间所有可能的连接方式，其他相关变量和集合可以参考本文符号说明部分。该超结构能够考虑到新鲜水的费用、处理单元的购置费用以及操作费用和管线连接费用等。

如式(1)所示，目标函数为最小化年均化总费用（），其包括新鲜水的费用、处理单元的购置费用以及操作费用和管线费用。

式中，是新鲜水的消耗量；是处理单元的污水处理量；是年操作时间；、以及是各项的费用系数；是年均化费用因子。

管线连接用线性的计算公式，其连接费用与连接个数为线性关系[16]。管线费用如式(2)所示。

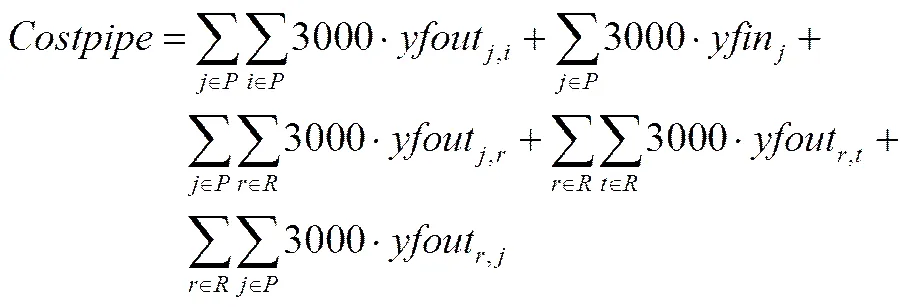
式中，和对应的为决定虚拟分流器和混合器是否连接的整型变量。

新鲜水从水源经过分流器分流后，被运输到各个用水单元，故其分流器处水的总流量等于其分流到各个用水单元的新鲜水流量fin之和，对应的质量守恒如式(3)所示。

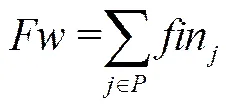
从系统的整体来看，输入新鲜水的量应该等于输出废水的量。故末端废水排泄处的总流量即为总的新鲜水用量，可以表示为所有用水单元的外排水总流量∑fout和所有污水处理单元的外排水总流量∑fout的加和，其质量守恒如式(4)所示。

(4)

用水单元的用水流量F在进口混合器处等于其来自新鲜水源、其他用水单元及废水处理单元的水流量之和（fin、∑fout及∑fout），质量守恒如式(5)所示，该式中的和都表示用水单元。

(5)

混合器处的水经用水单元使用后，要通过该用水单元出口处的分流器，被运输到其他用水单元及废水处理单元（fout和fout），因此F又等于该用水单元分流到其他单元的水流量之和，其质量守恒如式(6)所示。

(6)

废水处理单元的水流量F等于其进口混合器处总流量，即来自用水单元及其他废水处理单元供水的总和（fout及fout），其质量守恒如式(7)所示，该式中的和表示不同的废水处理单元。

(7)

污水经过处理单元后，经过分流器分流进入其他废水处理单元用水单元及排放到环境中。故流经废水处理单元的水流量也等于其出口处分流器的各个分流量之和（fout及fout），其质量守恒如式(8)所示。

(8)

末端废水排泄的虚拟混合器处的杂质的质量守恒如式(9)所示。

式中，cout是杂质的浓度。

用水单元进口的虚拟混合器处的杂质的质量守恒如式(10)所示。

, (10)

式中，cin是混合后用水单元的进口杂质的浓度。

废水处理单元进口的虚拟混合器处的杂质的质量守恒如式(11)所示。

, (11)

式中，cin是混合后废水处理单元进口杂质的浓度。

用水单元出口杂质含量为进口杂质含量与脱除的杂质含量M加和，其杂质的质量守恒如式(12)所示。

, (12)

,(13)

2 方法

由式(1)～式(13)构成的多杂质用水网络模型是一个复杂的MINLP问题。这主要是因为一些非凸约束决定的。例如，式(9)～式(12)是一类双线性等式约束。另外，目标函数中污水处理单元的设备投资是其处理水量的指数函数，这也增加了计算的困难。因此，针对式(9)～式(12)中存在的双线性约束，本文将利用分段线性松弛的方法经行处理，使这些难处理的等式约束转换成线性约束[16]。

对于双线性等式约束，首先对在其下界lo和上界up内将其分成个片段。如式(14)～式(16)，其中()是第段的下界而()是第段的上界，()表示分段的段数，()表示在第几分段内。

(14) (15) (16)

在第段内对应的变量为()，其相应的约束如式(17)～式(19)。

(17) (18) (19)

在第段内对应的变量为()，其相应的约束如式(20)～式(22)。

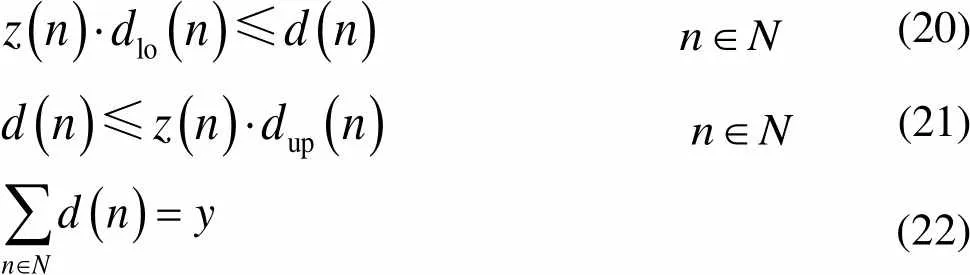
(20) (21) (22)

利用分段线性松弛的4个线性不等式逼近，如式(23)～式(26)。

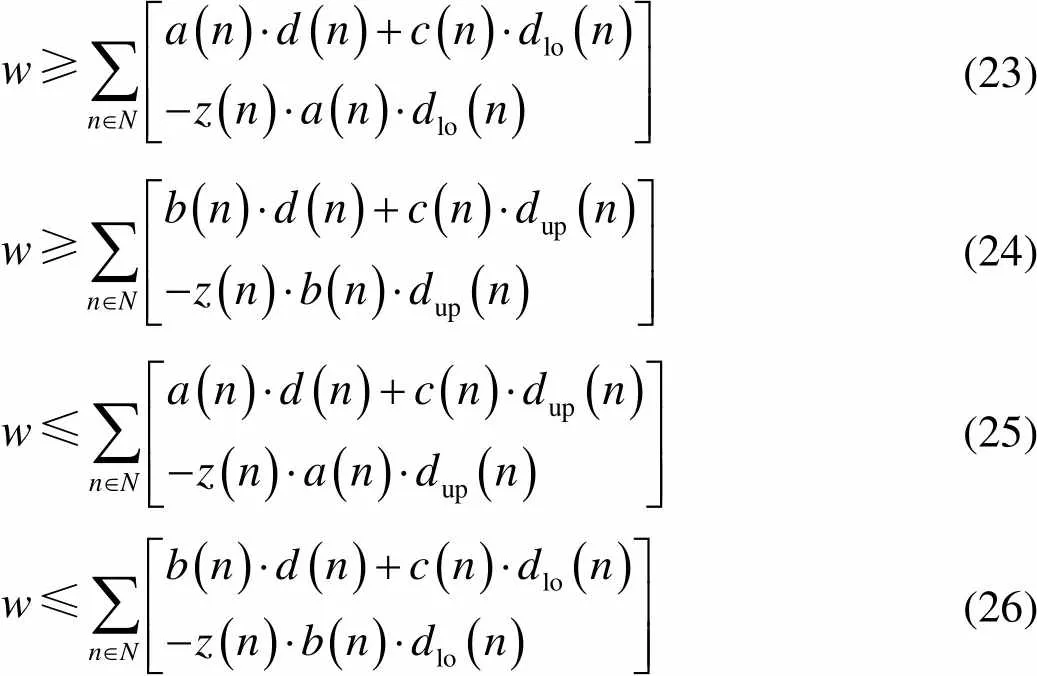
(23) (24) (25) (26)

(27) (28) (29) (30) (31) (32) (33)

该模型中的非线性项经过以上方法的处理后，其对应的MINLP问题可以转化为等效的MILP问题。现有的商业优化软件对MILP的求解算法已成熟，可求得全局最优解。

3 案例分析

本文案例取自文献[16]中多杂质用水系统的例子。该案例中包含1个新鲜水源、4个用水过程、2个污水处理单元、7个虚拟混合器及7个虚拟分流器。废水中含有A和B两种杂质，用水网络中的各种已知条件如表1和表2所示。其中，表1为用水单元关于不同杂质A和B的排放负荷以及进出口杂质浓度的上限，表2为污水处理单元杂质的脱除率和设备费用因子。

表1 　过程用水数据[16]

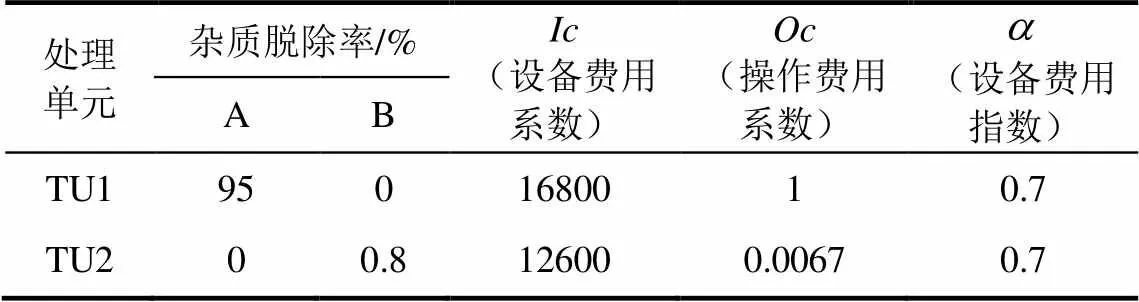
表2 污水处理单元数据[16]

本案例中，基建设备的年均化费用因子为0.1，年平均操作时间为8000h，新鲜水的单价为1 $/t。本文通过数学规划法，利用分段线性松弛的方法，使复杂的水网络模型转换为对应的MILP从而降低了计算的难度并获取全局最优解。

图2为文献[16]的设计结果，图3为本研究获得的最优结果。对比可以看出，两者的新鲜水用量都是40t/h。但该文献中的设计有15个连接数且为928057$/a。而由本研究方法得到的设计方案只有13个连接数且为914361$/a。连接数较少是因为降低了13696$/a。因为该文献中的用水单元2和用水单元3出现了交叉回用的情况。而在图3中，用水单元1的出口水全部供给用水单元2使用，而用水单元2和用水单元3出口的水全部回用进入单元4。显然，图3的设计中未出现交叉回用的情况。因此，相对于前人文献的设计结果，本研究所获得的设计方案的较小，即本文得到的设计方案更优。

4 结论

本文研究了含有再生循环单元的多杂质用水网络的超结构，对其数学规划模型进行分析和处理。利用分段线性松弛的方法，使复杂的MINLP问题转换为对应的混合整数线性规划问题。降低了问题求解的难度且能获取全局最优解，得到一个经济性更好的多杂质用水网络。在商业优化软件GAMS平台上，对文献中的工业案例进行优化分析。案例结果表明优化方案中管线连接数为13，这比文献中的15条管线少，总的年度化费用降低了大约1.5%。因此，利用线性松弛的全局优化方法对设计更优的多杂质用水网络有着重要的意义。

符号说明

Af——基建设备费用的年投资率 a——变量分段的下界 b——变量分段的上界 Costpipe——管线费用，$/a c——变量在分段的值 card——变量分段的段数 cin——进口处水杂质浓度，μL/L cout——出口处水杂质浓度，μL/L d——对应分段变量的值 F——用水处理单元的水流量，t/h Fr——废水处理单元的水流量，t/h Fw——新鲜水的流量，t/h fin——新鲜水到用水单元的流量，t/h fout——虚拟分流器各个分支的水流量，t/h Hc——新鲜水的单价，$/t Hour——年平均操作时间，h Ic——设备费用系数 M——杂质含量，kg/h Oc——废水处理单元操作费用系数因子 P——用水单元集合 R——废水处理单元集合 S——废水中杂质的集合 TAC——总年均化费用，$/a w——双线性项对应的值 x——双线性项变量 y——双线性项变量 yfin——入口连接管线存在与否的整型变量 yfout——出口连接管线存在与否的整型变量 z——分段的整型变量 α——废水处理单元设备费用指数因子 下角标 i，j——用水单元 n——变量分段的个数 r，t——废水处理单元 s——杂质种类

[1] TAKAMA N，KURIYAMA T，SHIROKO K，UMEDA T．Optimal water allocation in a petroleum refinery[J]. Computers & Chemical Engineering，1980，4（4）：251-258．

[2] WANG Y P，SMITH R．Wastewater minimisation[J]. Chemical Engineering Science，1994，49（7）：981-1006．

[3] FOO D C Y．A generalised guideline for process changes for resource conservation networks[J]. Clean Technologies and Environmental Policy，2013，15（1）：45-53．

[4] ZHENG X，FENG X，SHEN R，et al．Design of optimal water-using networks with internal water mains[J]. Industrial & Engineering Chemistry Research，2006，45（25）：8413-8420．

[5] KUO W C，SMITH R．Design of water-using systems involving regeneration[J]. Process Safety and Environmental Protection，1998，76（2）：94-114．

[6] BAI J，FENG X，DENG C．Graphically based optimization of single-contaminant regeneration reuse water systems[J]. Chemical Engineering Research and Design，2007，85（8）：1178-1187．

[7] TAN Y L，MANAN Z A，FOO D C Y．Retrofit of water network with regeneration using water pinch analysis[J]. Process Safety and Environmental Protection，2007，85（4）：305-317．

[8] NG D K S，FOO D C Y，TAN R R．Automated targeting technique for single-impurity resource conservation networks．Part 1：Direct reuse/recycle [J]. Industrial & Engineering Chemistry Research，2009，48（16）：7637-7646．

[9] DENG C，FENG X．Targeting for conventional and property-based water network with multiple resources[J]. Industrial & Engineering Chemistry Research，2011，50（7）：3722-3737．

[10] DOYLE S J，SMITH R．Targeting water reuse with multiple contaminants[J]. Process safety and Environmental Protection，1997，75（3）：181-189．

[11] LIU L，WANG J，SONG H，et al．Synthesis of water networks for industrial parks considering inter-plant allocation[J]．Computers & Chemical Engineering，2016，91：307-317．

[12] FENG X，BAI J，WANG H，et al．Grass-roots design of regeneration recycling water networks[J]. Computers & Chemical Engineering，2008，32（8）：1892-1907．

[13] FARIA D C，BAGAJEWICZ M J．On the appropriate modeling of process plant water systems[J]. AIChE Journal，2010，56（3）：668-689．

[14] BAI J，FENG X，DENG C．Optimal design of single-contaminant regeneration reuse water networks with process decomposition[J]. AIChE Journal，2010，56（4）：915-929．

[15] BERGAMINI M L，GROSSMANN I，SCENNA N，et al．An improved piecewise outer-approximation algorithm for the global optimization of MINLP models involving concave and bilinear terms [J]. Computers & Chemical Engineering，2008，32（3）：477-493．

[16] KARUPPIAH R，GROSSMANN I E．Global optimization for the synthesis of integrated water systems in chemical processes[J]. Computers & Chemical Engineering，2006，30（4）：650-673．

[17] YANG L，SALCEDO-DIAZ R，GROSSMANN I E．Water network optimization with wastewater regeneration models[J]．Industrial & Engineering Chemistry Research，2014，53（45）：17680-17695．

[18] ALNOURI S Y，LINKE P，EL-HALWAGI M．Optimal interplant water networks for industrial zones：addressing interconnectivity options through pipeline merging[J]. AIChE Journal，2014，60（8）：2853-2874．

[19] ILAYA-AYZA A E，BENÍTEZ J，IZQUIERDO J，et al．Multi-criteria optimization of supply schedules in intermittent water supply systems[J]．Journal of Computational and Applied Mathematics，2017，309：695-703．

[20] WICAKSONO D S，KARIMI I A．Piecewise MILP under‐and overestimators for global optimization of bilinear programs[J]. AIChE Journal，2008，54（4）：991-1008．

Global optimization for multi-contaminant water networks with regeneration recycling unit

CHEN Xiaolu1，CHANG Chenglin2，WANG Yufei1，FENG Xiao2

（1College of Chemical Engineering，China University of Petroleum，Beijing 102249，China；2New Energy Institute，China University of Petroleum，Beijing 102249，China）

The introduction of regeneration recycling unit can largely reduce freshwater consumption and wastewater discharge. The current optimization model of multiple contaminants water networks with regeneration recycling unit is a non-convex mixed-inter nonlinear programming problem（MINLP）. Solving directly without any strategy is very hard，slow and easily trapped into the local optimal solutions. In this paper，a global optimization strategy with piecewise linear relaxation was proposed. With the strategy the complex problem as an MILP model can be reformulated. The computational efforts can be reduced largely and the optimum solution can be obtained. A case study was illustrated to demonstrate the capability of our strategy and the global optimization solution had a significant impact on the total annual cost.

multi-contaminant water networks；mathematical model；piecewise linear relaxation；global optimization

TQ021.8

A

1000–6613（2017）06–2064–06

10.16085/j.issn.1000-6613.2017.06.014

2016-09-13；

2016-11-17。

国家重点基础研究发展计划（2012CB720500）及国家自然科学基金（21576286）项目。

陈晓露（1993—），女，硕士研究生。联系人：王彧斐，博士，副教授。E-mail：wangyufei@cup.edu.cn。