基于混沌映射理论的身份验证蜻蜓密钥交换协议

刘天华, 冯学帅, 朱宏峰

(沈阳师范大学 科信软件学院, 沈阳 110034)



基于混沌映射理论的身份验证蜻蜓密钥交换协议

刘天华, 冯学帅, 朱宏峰

(沈阳师范大学 科信软件学院, 沈阳 110034)

蜻蜓协议是一种基于密码身份验证的密钥交换协议,该协议已经成为IETF的一个互联网使用的候选协议。然而,Harkins分析了该协议的安全性后,设计了一个算法成功地在一个多项式的时间内完成了对蜻蜓密钥交换协议的攻击。提出一种采用混沌映射理论设计算法的改进蜻蜓密钥交换协议,该协议基于混沌映射的离散对数问题CMBDLP和混沌映射的Diffie-Hellman问题CMBDHP,使用有限域乘法算法取代传统的混沌映射对称加密的方法,并且算法中引入Hash函数的计算,一方面提高了算法的效率,另一方面提高了算法的安全性。因此,与目前的蜻蜓协议相比,该协议更安全、更高效、更实用,可以抵抗密码猜测攻击、重放攻击、欺骗攻击、内部攻击以及Harkins提出的攻击,并且实现了完全正向保密和已知密钥保密。

密码身份验证; 网状网络; 混沌映射; 蜻蜓协议

0 引 言

网状网络是一种可以在网络上通过网格节点传输数据的网络拓扑结构,也被称为“多跳网络”,是一个动态的、可扩展的网络结构。在这种网络结构中,所有节点协同传输数据。网状网络可分为有线网状网络和无线网状网络2种。目前,无线网状网络[1]非常流行,它是一种自组织的网络,网络上的节点通过无线链接来实现无线设备之间的信息传输。无线网状网络优于过去的无线局域网。在传统的无线局域网中,如果用户想要和别人交流,就必须首先访问一个固定的接入点(AP),使用这种方法的网络称之为单跳网络。然而,在网状网络(多跳网络)中,可以使用任何无线设备节点作为接入点(AP)或路由。这种网络的优势在于如果最近的节点由于流量大导致拥挤,数据可以选择流量小的节点来完成整个传输任务。因此,网络环境中的传输过程如下:数据先从一个节点到达其他多个节点,然后到达最终目标地址。这种方式也被称为多跳访问。由于网状网络的优势,越来越多的研究人员开始设计网状网络中的协议。

目前,许多协议都已经被应用网状网络中。2009年,Clancy等[2]提出了EAP-GPS作为一种轻量级的共享密钥认证协议。2010年,Kaufman等人提出了IKEv2[3]作为第二代因特网密钥交换控制协议。但是,所有这些协议都不能抵抗字典攻击。为了解决字典攻击问题,2012年,D. Harkins[4]提出了一种基于离散对数的密钥交换协议,并命名为蜻蜓密钥交换协议。该协议不仅能抵抗主动攻击,也可以抵抗被动攻击,和离线字典攻击。

然而,蜻蜓协议也存在缺陷,2013年Dylan Clark等[5]成功的攻击了该协议,他们指出如果攻击者选择多组生成器,便可以使用离线字典攻击蜻蜓协议,所以必须采取一些方法来提高蜻蜓密钥交换协议的安全性。传统的混沌映射是一个数学概念,可以被连续时间和离散时间参数化。由于混沌映射的确定性、有界性和伪随机等优势,其已广泛地应用于密钥协商协议。此外,混乱映射也能够产生伪随机。所以混沌映射不需要如时间戳、模幂运算,椭圆曲线[6]等数学计算也可以抵御常见的攻击,如主动出击,被动攻击、字典攻击等。

本文使用混沌映射的特性来提高蜻蜓协议的安全性,将蜻蜓协议与混沌映射相结合,确保改进的蜻蜓协议更安全、更高效。本文改进之处如下:1)通过混沌映射有效地提高了蜻蜓协议的效率和安全性。2)该方案能够真正抵抗主动攻击,被动攻击,甚至是Dylan Clarke提出的离线词典攻击。3)该方案的实用性、稳定性、安全性在原有的基础上进一步提高。

1 基本理论

1.1 网状网络

在网状网络这种拓扑结构中,网络上每个节点都会传递数据。网状网络可以通过洪泛和路由技术传递信息。信息通过路由器沿着传输路径从一个节点跳跃到另一个节点,直到到达目标地址。网络必须保证每个节点间的连线完整,且必须保证当网络拓扑中某节点失效或无法服务时能够重新配置以避免产生网络路径无法使用的问题。因此,在网状网络中,一些典型的自愈算法,如最短路径算法,就显得至关重要。当网络中一个节点发生故障或一个连接无法服务时,自愈机制会自动地在网路中的源地址和目标地址之间的多条路径中重新配置。所以,一般而言网络通常都是高度可信赖的。

网状网络是一种完全连接网络。完全连接有线网络的优势表现在其安全性和可靠性,在一条连接上的问题只会影响附属在两端的节点。然而,在这样的网络中,电缆的数量会随着节点数的增加而增加,致使成本也会迅速上升。

作为一种特别的网络,网状网络与移动自组织网络密切相关。网状网络体系结构由3部分组成:接入点、无线路由器和客户端,三者彼此协同工作。其中,接入点、无线路由器确保了在不同网络中的连通性,并使得客户端能够通过无线路由器接入网络。此外,客户端也拥有一定的路由功能,致使设备可以形成一个自组织网络。网状网络的体系结构如图1所示。

1.2 Chebyshev混沌映射

令n为整数,变量x∈[-1,1]。Chebyshev多项式Un(x):[-1,1]→[-1,1],Un(x)=cos(narccos(x))。由第二类Chebyshev多项式的特征方程

(1)

可推出Chebyshev多项式映射Un:R→R满足以下的递推关系[7]:

(2)

Chebyshev多项式最重要的一个特性是半群性质,表示为

(3)

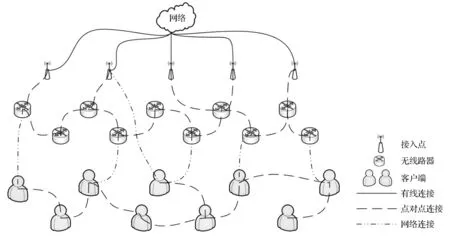
图1 网状网络的体系结构

为了提高安全性,赵耿等[8]证明了在区间(-∞,+∞)半群属性适用于Chebyshev多项式。改进的Chebyshev多项式用于拟议的协议:

当n≥2,x∈(-∞,+∞),N是一个大素数时,有

(4)

显然,

(5)

定义1 多项式的半群性质:

(6)

定义2 根据x和y,很难找到一个整数s,使得Us(x)=y,即基于混沌映射的离散对数问题(CMBDLP)。

定义3 根据x,Ur(x)和Us(x),很难找到Urs(x),即基于混沌映射的Diffie-Hellman问题(CMBDHP)。

2 蜻蜓协议

蜻蜓协议[9]是一个基于离散对数密码的口令认证密钥交换协议。所以蜻蜓协议的操作也可以用于椭圆曲线或有限领域。首先定义2个用户,然后形成一个蜻蜓协议流。蜻蜓协议所遵循的步骤和流程如图2所示。

P∈Q1.gA,kA∈{1,…,q}gB.kB∈{1,…,q}2.sA=gA+kAsB=gB+kB3.EA=P-kAEB=P-kB4. sA,EA → sB,EB ←5.ss=(PsBEB)gA=PqBgA A=H(ss‖EA‖sA‖EB‖sB) →验证A6.验证B B=H(ss‖EB‖sB‖EA‖sA) ←ss=(PsAEA)gB=PqAgB7.计算共享密钥K=H(ss‖EA·EB‖(sA+sB)modq)

图2 蜻蜓协议的流程

Fig.2 The process of dragonfly protocol

蜻蜓协议工作流程如下:

1) Alice和Bob从Q中取一个共享的密码元素P(P∈Q)作为共享密码。

2) Alice从1到q中随机选取2个标量gA和kA,计算标量sA=gA+kA,EA=p-kA,然后将sA和EA发送给Bob。同样的,Bob从1到q中随机选取2个标量gB和kB,计算标量sB=gB+kB,EB=p-kB,然后将sB和EB发送给Alice。

3) Alice计算出共享密码ss=(PsBEB)gA=PgBgA,Bob计算出共享密码ss=(PsAEA)gB=PgAgB。

4) Alice发送给Bob一个加密哈希函数A=H(ss‖EA‖sA‖EB‖sB),Bob发送给Alice一个加密哈希函数B=H(ss‖EB‖sB‖EA‖sA)。

5) Alice和Bob相互验证并检查哈希函数是否正确,如果正确,则建立一个共享密钥K=H(ss‖EA·EB‖(sA+sB)modq)。

正如上文所述,该方案在密钥协商的过程中存在一些问题:

1) D.Clarke指出关于基础群没有任何可以做的假设。此外,他认为离散对数的计算也没有安全要求所要的级别。在D.Clarke的论文中,他描述了攻击这类协议的一种模型和一组实现方法。

2) D.Clarke所提出的攻击方法是字典攻击。在破解密码和密钥时,攻击者就会逐一尝试可能的字母和数字的密码组合,直到找到这个密码或密钥的正确的组合形式。

3) 攻击者使用以下3个步骤启动离线字典攻击:获取被攻击者的密码元素P;建立一个有效的响应B绕过身份验证,此时,被攻击者不知道密码已经被破解;通过推导出的密钥K去破解通信密码。

因此,需要扩展字段并且增加随机标量的方法来抵抗字典攻击。

3 身份验证蜻蜓协议

一旦再次发生出现在原有的蜻蜓协议上的问题,将采取一系列的解决措施:

1) 使用HPW代替原来的密码元素P。因为P属于有限循环群Q,易于被获取,所以使用一个预定义的加密哈希函数H(IDA‖IDB‖PW)去获得HPW的值。此时,再有攻击者进行字典攻击时,就需要先花费大量的时间去获取这个值。

2) 与原蜻蜓协议相比,增加一个高熵变量x和n可以使新的蜻蜓密钥交换协议具有更高的安全性。

3) 使用随机标量gA,gB,kA和kB生成Chebyshev多项式E=UmUHPWUr(x),以确保字典攻击无法成功。因为攻击者必须猜测2个输入值HPW(HPW是一个低熵的密值)和m(m是一个高熵的绝对密值),显然,这是不可行的。

大部分基于混沌映射实现关键协议或协议加密消息通常采用基于Diffie-Hellman的混沌映射(CDH)问题得到相同的用户和服务器之间传输的密钥加密/解密消息。而本文的方案只使用CDH得到临时密钥用于附加信息,从而使计划更有效率,保护用户的隐私信息。显然,本文提出的方案比前者更有效。

4) 使用Chebyshev混沌映射代替离散对数。Chebyshev多项式Un(x):[-1,1]→[-1,1]被定义为Un(x)=cos(narccos(x))。该方案的计算速度更快、占用的内存和带宽更小,且效率更高。在第五章将会具体分析该方案的安全与效率。

改进的身份验证蜻蜓协议所遵循的步骤和流程如图3所示。

1) Alice和Bob使用共享密钥PW并计算HPW=H(IDA‖IDB‖PW)。

2) Alice随机选取2个元素gA和kA,并计算出EA=UkA(x)UHPWUgA(x),将EA,UgA(x)发送给Bob。同样,Bob计算出EB=UkB(x)UHPWUgB(x),将EB,UgB(x)发送给Alice。

4)Alice计算共享密钥 SS=UkAUkB(x),同样,Bob计算共享密钥SS=UkBUkA(x)。

5)Bob发送B=H(SS‖EB‖UgB(x)‖EA‖UgA(x))给Alice。Alice接到B值后进行验证。

6)Alice和Bob确认身份。成功后,将生成共享密钥K=H(SS‖EA‖EB)。

该方案不仅可以抵抗常见攻击,也可以抵御DylanClark所提出的攻击方案[5]。DylanClark的攻击方案之所以能成功实现,是因为能够成功搜索到算法中的关键值sB,EB和A。而本文提出的方案由于CMBDLP和CMBDHP困难致使无法获取EB和gB的值。

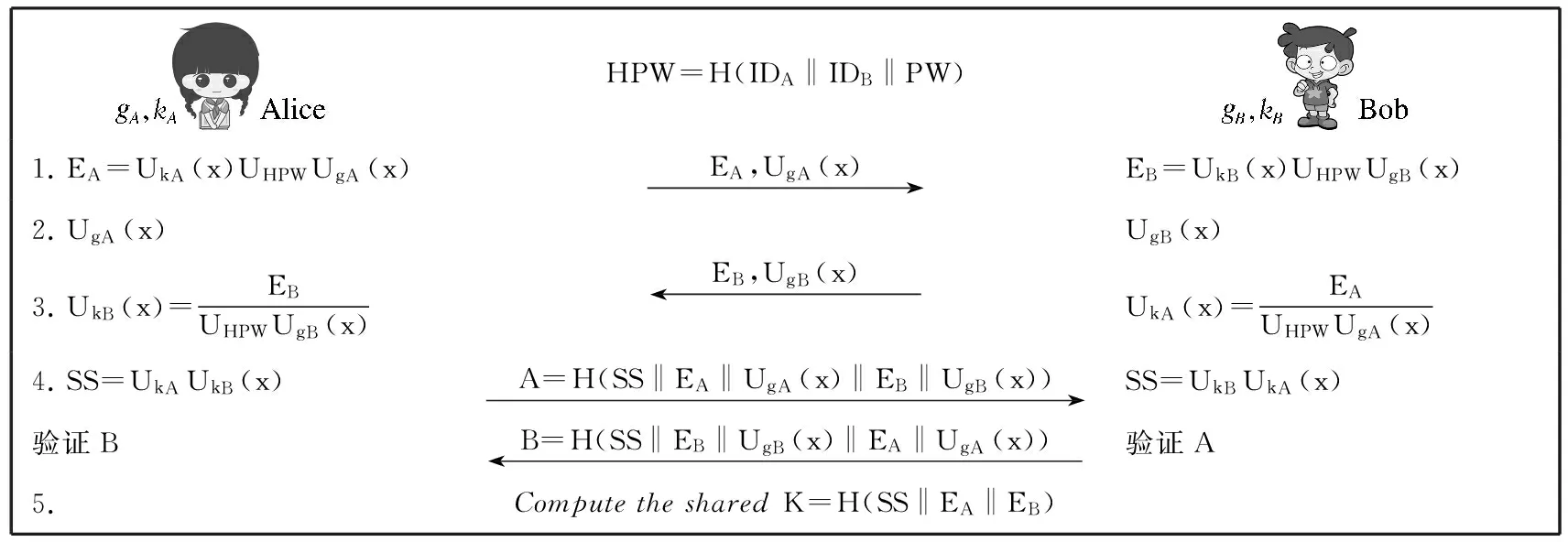
HPW=H(IDA‖IDB‖PW)1.EA=UkA(x)UHPWUgA(x) EA,UgA(x) →EB=UkB(x)UHPWUgB(x)2.UgA(x)3.UkB(x)=EBUHPWUgB(x) EB,UgB(x) ←UgB(x)UkA(x)=EAUHPWUgA(x)4.SS=UkAUkB(x) A=H(SS‖EA‖UgA(x)‖EB‖UgB(x)) →SS=UkBUkA(x)验证B B=H(SS‖EB‖UgB(x)‖EA‖UgA(x)) ←验证A5.ComputethesharedK=H(SS‖EA‖EB)

图3 改进的身份验证蜻蜓协议

Fig.3 The improved authentication dragonfly protocol

4 安全分析

4.1 完全正向保密

本文提出的方案中会话密钥[10]SS与Alice和Bob随机生成的gA,gB,kA,kB值相关。所以即便攻击者最后获取了gA,gB,kA,kB,也无法在同一时间计算相关参数的值。而在没有这些参数的值的情况下,攻击者无法计算出共享密钥。通过上述的处理方式,本文很好的达到了完全正向保密的要求。

4.2 已知密钥保密

由于kA,kB在所有会话中都是独立且不同的,因此即使攻击者获得了一个会话密钥SS=UkAUkB(x)和一对随机数kA、kB,攻击者在不知道其他随机数的条件下也无法计算出其他会话密钥的值。

所以,本文所提出的协议可以实现会话密钥保密和已知密钥保密[11]。

4.3 密码猜测攻击

如果攻击者试图使用密码猜测攻击,他将由于在计算过程中遇到的包括四个大随机变量gA,kA,gB,kB.和K=H(SS‖EA‖EB)的计算而无法实现密码猜测攻击。

密码猜测攻击只能破解一个函数与一个低熵变量,所以只要至少插入一个大随机变量就可以抵御这种攻击。而本文的协议通过高熵变量gA,kA,gB,kB和HPW组成复杂的功能表达式,例如:EA=UKA(x)UHPWUgA(x)。此外,当使用切比雪夫混沌映射Un(x)=cos(narccos(x))时,还存在另外2个高熵变量x和n,因此,密码猜测攻击是无法成功的。

4.4 重放攻击

本文所提出的协议能够抵抗重放攻击,因为kA和kB是匿名的,在整个传输过程中从不出现。因此,攻击者将无法获取kA和kB的值。此外,由于每次的所使用的值并不相同,所以攻击者无法重放攻击被加密的数据传输协议。

4.5 欺骗攻击

在本方案中,Alice和Bob必须通过哈希函数值A=H(SS‖EA‖UgA(x)‖EB‖UgB(x)) 和B=H(SS‖EB‖UgB(x)‖EA‖UgA(x))才能相互通过验证。只有当他们都通过身份验证,才能计算K值。

4.6 内部攻击

本文提出的方案需要计算的密钥为HPW=H(IDA‖IDB‖PW),ID是哈希函数的参数信息,攻击者不能直接获取ID。所以本协议能够抵抗内部攻击。

在上述的总结中,本文提出的协议是安全的。各安全方案与本文所提出的身份验证蜻蜓协议之间安全性的比较如表1所示。

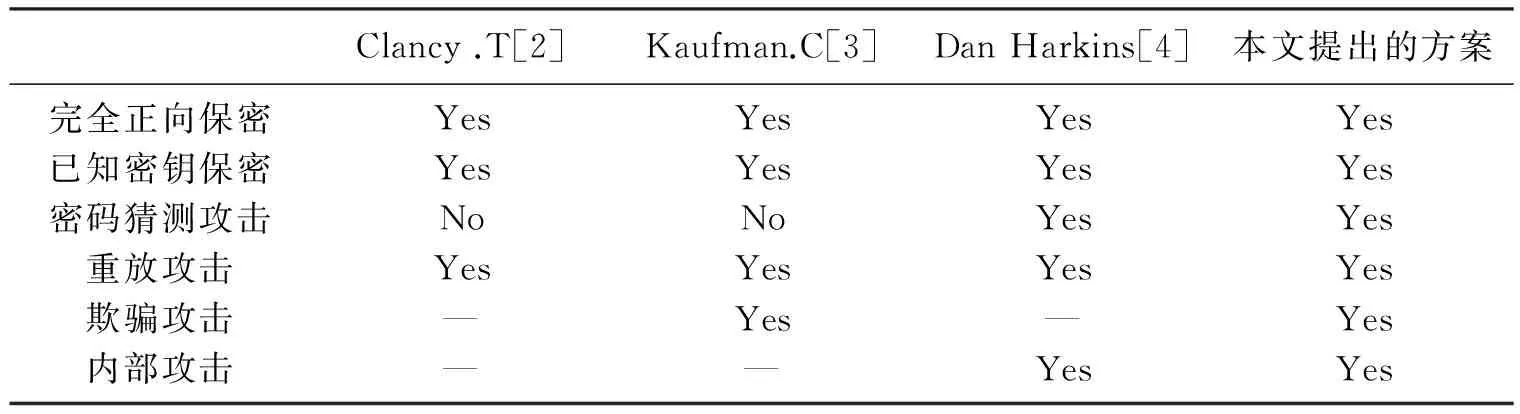
表1 各安全方案间的安全性比较

注: —:未涉及; Yes: 支持该项安全; No: 不支持该项安全。

5 效率分析

利用切比雪夫多项式,提出了一种密钥交换协议。与原有的蜻蜓协议相比,切比雪夫多项式计算问题时计算速度更快,内存使用更少,更加节省资源。本文提出的协议没有模幂运算和椭圆曲线标量乘法对计算时间的消耗。

与RSA、ECC和双线性映射[12]相比,切比雪夫多项式计算问题时计算速度更快,内存使用更少,更加节省资源和带宽。混沌映射加密算法,混沌意味着在某些非线性系统中可以在不需要任何随机因素的情况下就可以出现类似随机行为的伪随机现象。混沌系统具有确定性、有界性、初始参数敏感性和不可预测性等特点。混沌映射加密算法是基于混沌映射中离散对数问题和Diffie-Hellman难题这2个困难问题利用切比雪夫独特的半群性质提出的一种加密算法。与ECC加密算法相比,混沌映射加密算法避免了标量乘法模幂运算的计算,有效地提高了算法效率。

然而,王兴元提出了几种方案来解决切比雪夫多项式计算问题[13]。确切的说,在一个n和p均为1 024个位长、内存1 024 MB、处理器2 600 MHz的英特尔奔腾4处理机下,单向散列操作、对称加密/解密操作、一个椭圆曲线点乘法操作和切比雪夫多项式操作所需的计算时间分别为0.000 5 s、0.008 7 s、0.063 075 s和0.021 02 s。其中,异或操作的计算成本与操作相比可以忽略。结果显示,在底层有限域中一个配对操作所需时间是相同有限域下椭圆曲线密码体制点标量乘法的10倍多[15]。

通过上述分析,可以得出下述结论:

Up≈10Um,Um≈3Uc,Uc≈2.42Us,Us≈17.4Uh,

将上述公式合并为一个式子,可以更加直观地反映算法的时间关系:

Up≈10Um≈30Uc≈72.6Us≈1 263.24Uh,

其中,Up是双线性对操作所需时间,Um是一个标量乘法操作所需的时间,Uc是在Chebyshev多项式中计算Un(x)模p的时间,Us是对称加密算法所需的时间,Uh是Hash操作所需的时间。每个方案各阶段的执行时间比较如表2所示。

表2 各安全方案间的执行效率比较

注: 其中,Uh: Hash操作所需时间;Uc: 在Chebyshev多项式中计算Un(x)模p的时间;Us: 对称加密算法所用的时间;Ue: 求幂运算所用的时间。

6 结 论

本文的提出的基于混沌映射理论的身份验证蜻蜓密钥交换协议表现出简单,高效率和良好的性能。首先,文中使用混沌映射,而不是离散对数(模幂运算和椭圆曲线标量乘法)。然后,介绍了网状网络知识、混沌映射和蜻蜓协议。最后,利用本文提出的方案和原有方案及其他一些协议做了比较。根据比较结果得出本文提出的协议更适合应用程序。

[ 1 ]宋文,方旭明. 无线网状网研究与发展[J]. 铁道学报, 2007,29(2):96-103.

[ 2 ]CLANCY T,TSCHOFENIG H. Extensible Authentication Protocol-Generalized Pre-Shared Key (EAP-GPSK) Method[EB/OL]. [2016-10-17]. https:∥tools.ietf.org/html/rfc5433,IETF RFC 5433.

[ 3 ]KAUFMAN C,HOFFMAN P,NIR Y,et al. Internet Key Exchange Protocol Version 2 (IKEv2)[EB /OL]. [2016-10-19]. https:∥www.rfc-editor.org/rfc/rfc5996.txt,IETF RFC 5996.

[ 4 ]HARKINS D. Dragonfly key exchange-internet research task force internet draft[EB/OL]. [2016-09-26]. http:∥tools.ietf.org/html/draft-irtf-cfrg-dragonfly-00.

[ 5 ]CLARKE D,FENG H. Cryptanalysis of the dragonfly key exchange protocol[J]. Information Security Iet, 2014,8(6):283-289.

[ 6 ]刘明来,赵耿,魏广征,等. 基于混沌系统的椭圆曲线密码算法研究[J]. 北京电子科技学院学报, 2013(4):15-19.

[ 7 ]CHEN T Y,LEE C C,HWANG M S,et al. Towards secure and efficient user authentication scheme using smart card for multi-server environments[J]. J SUPERCOMPUT, 2013,66(2):1008-1032.

[ 8 ]ZHAO G,SUN J H,ZHAO F. Key agreement scheme based on Chebyshev polynomials over finite fields[J]. Application Research of Computers, 2012,29(10):3794-3796.

[10]MAJHI B,KAR J. An Efficient Password Security of Multi-Party Key Exchange Protocol Based on ECDLP[J]. International Journal of Computer Science & Security, 2009,3(5):405-413.

[11]李文敏. 认证密钥协商协议的设计与应用[D]. 北京:北京邮电大学, 2012.

[12]张丽,郝身刚,岳贤锋. 基于双线性映射的匿名跨域认证方案[J]. 河南师范大学学报(自然科学版), 2013,41(1):155-158.

[13]WANG X,ZHAO J. An improved key agreement protocol based on chaos[J]. Communications in Nonlinear Science & Numerical Simulation, 2010,15(12):4052-4057.

[14]GUO C,CHANG C C. Chaotic maps-based password-authenticated key agreement using smart cards[J]. Communications in Nonlinear Science & Numerical Simulation, 2013,18(6):1433-1440.

[15]BARRETO P S L M,LYNN B,SCOTT M. On the Selection of Pairing-Friendly Groups[M]. Springer Berlin Heidelberg:Selected Areas in Cryptography, 2003:17-25.

Reinforcement dragonfly key exchange protocol based on chaotic maps

LIU Tianhua, FENG Xueshuai, ZHU Hongfeng

(Software College, Shenyang Normal University, Shenyang 110034, China)

Dragonfly is an exchange protocol key based on password authentication,which has been submitted to the IETF and became a candidate standard for general internet use. However,Harkins analyzed the security of this protocol and designed an algorithm to attack it. This protocol was attacked successfully in a polynomial time. In this paper,we propose an exchange protocol key called Improved Dragonfly Key Exchange Protocol based on CMBDLP and CMBDHP in chaotic maps with multiplication in finite field algorithm to replace the traditional method of chaotic maps-symmetric cryptography for achieving high-efficiency. The introduction of the Hash function calculation in our algorithm improves the efficiency and the security of the algorithm. Therefore, this proposed protocol is more secure,efficient,and practical compared with the old Dragonfly protocol,and can resist password guessing attack,replay attack, spoofing attacks, internal attack and the attack raised by Harkins specially,and achieve perfect forward secrecy and known-key secrecy.

password authentication; mesh networks; chaotic; dragonfly protocol

1673-5862(2017)02-0240-07

2016-11-02。

辽宁省教育科学“十三五”规划项目(JG16DB406)。

刘天华(1966-),男,辽宁沈阳人,沈阳师范大学教授,博士; 通信作者: 冯学帅(1993-),男,内蒙古包头人,沈阳师范大学硕士研究生; 朱宏峰(1978-),男,辽宁沈阳人,沈阳师范大学教授,博士。

TP393.08; TN918.1

A

10.3969/ j.issn.1673-5862.2017.02.022