具有执行器饱和切换系统的控制

景 丽, 董秋阳

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)



具有执行器饱和切换系统的控制

景 丽, 董秋阳

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

主要研究了一类具有执行器饱和的切换系统的控制问题,探究当切换系统中执行器出现饱和时,系统要达到渐近稳定需要满足的充分条件,并证明所得结论。首先,针对执行器饱和系统,处理饱和项至关重要。利用扇形区域法的思想,成功解决饱和项的处理问题。其次,为系统选择适当的李雅普诺夫函数,进而研究获得执行器饱和切换系统的的渐近稳定判据。然后,为使求解更加方便快捷,对获得系统渐近稳定的充分条件做变形处理,将其转换成线性矩阵不等式形式。最后,进行吸引域大小的估计,结合相应的仿真算例,证明了研究成果是有效可行的。

切换系统; 执行器饱和; Lyapunov理论; 线性矩阵不等式

0 引 言

限制和约束广泛存在于实际生产生活中,其中饱和执行器会很大程度上对系统整体性能造成破坏,更严重的将引起系统的不稳定。一些离散或连续的子系统,在相应切换规则的严格控制下,会巧妙组合成复杂的切换系统。本文针对具有执行器饱和切换系统的控制问题进行研究是十分必要的。对于饱和系统的研究成果十分丰富,如文献[1-5]。文献[6]是饱和控制系统研究中的重要成果,由Sontag等人在1990年完成,指出当饱和线性系统的输入有界渐近零可控时,系统将达到全局稳定,此时将有光滑非线性控制器出现在系统之中。文献[7-10]以执行器饱和线性系统研究成果为基础,进一步探究饱和对切换系统的影响,用凸优化问题解决吸引域大小的估计。

本文主要研究执行器饱和切换系统的控制问题,巧妙地将执行器饱和与切换系统相结合,在饱和项的处理,控制器的设计方面均有良好的突破。

1 问题描述

考虑执行器饱和切换系统:

(1)

其中:x∈Rn为系统状态向量;u∈Rm为控制输入向量;Ai,Bi为适当维数的常矩阵;i=1,2,…,N。饱和非线性函数sat(·)定义如下:

sat(u)=[sat(u1),sat(u2),…,sat(um)]T

其中δ>0。

引入状态反馈控制律:

(2)

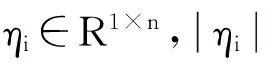
本文探究当切换系统的执行器出现饱和现象时,系统想要达到稳定所需满足的条件。主要涉及到相应状态反馈控制器的设计以及系统最大吸引域的估计。

下面给出进行本文研究需要的相关定义、定理等。

定义1(椭球集合)[11]P>0,P∈Rn×n,ρ>0为标量,定义椭球体为

定义3(吸引域)[11]假设系统的初始点和解分别为x(0)=x0∈Rn,φ(t,x0),那么系统的吸引域是:

1) S<0;

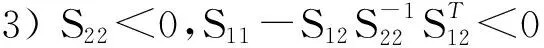
引理2[12]给定矩阵A、L、E、F, 若FTF≤I,则有以下不等式成立

其中:α>0,F>0。

2 执行器饱和切换系统的控制及吸引域估计

2.1 执行器饱和切换系统的控制

定理1 对于执行器饱和切换系统(1),如果在控制器(2)作用下存在满足如下不等式的矩阵Qi∈Rm×n,i=1,2,…,N和正定矩阵Ni>0,那么系统(1)在原点局部渐近稳定。

证明 对于式(2),由范数的三角不等式性质可得

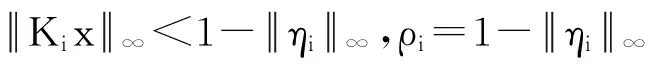
[(Ai+BiKi)x+Biηisat(x)]TPix+xTPi[(Ai+BiKi)x+Biηisat(x)]=

令

(3)

(4)

由引理2得到

2.2 吸引域估计

根据定理1给出的系统稳定条件,借助椭球体参考集进行吸引域的估计,进而获得最大的吸引域。

需要解决如下凸优化问题:

(5)

(6)

(7)

其中式(5)是系统稳定的条件,式(6)将吸引域限制在椭球体内,式(7)表示椭球包含在多面体内。

式(6)等价于

(8)

式(7)等价于

(9)

于是优化问题可以转化为

(10)

3 仿真算例

对于执行器饱和切换系统(1)

令i=1,2, 取系统(1)的2个子系统:

设系统状态矩阵、输入矩阵为

另外设

利用LMI工具箱求得式(10)的解,如下:

γ1=18.636 0, γ2=6.336 3,

系统初始状态选为:x=(2,0.9)T, 系统(1)在状态反馈控制器(2)的作用下渐近稳定,如图1、图2所示。

图1 系统状态轨迹

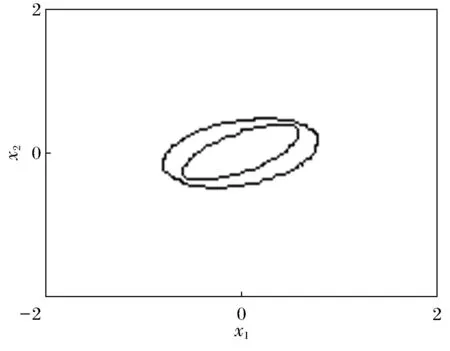
图2 系统吸引域图

4 结 论

本文所研究的是复杂的切换系统,并且系统包含的执行器饱和,这加大了系统研究的难度。执行器饱和的饱和项处理问题运用扇形区域法思想解决。基于李雅普诺夫稳定性理论,并利用线性矩阵不等式知识,给出系统实现渐近稳定需要满足的条件。选用椭球体为参考集,进一步估计吸引域的大小。

[ 1 ]HOU L, ANTHONY N. Asymptotic stability of systems with saturation constraints[J]. IEEE Transaction on Automatic Control, 1998,43(8):1148-1154.

[ 2 ]BLANCHINI F. Control of linear systems with regulation and input constraints[J]. Communications and Control Engineering, 2000,19(11):46-53.

[ 3 ]BERNSTEIN D S, MICHEL A N. A chronological bibliography on saturating actuators[J]. International Journal of Robust and Nonlinear Control, 1995,5(5):374-381.

[ 4 ]SABERI A, LIN Z, TEEL A R. Control of linear systems with saturating actuators[J]. IEEE Transaction on Automatic Control, 1996,41(3):368-378.

[ 5 ]俞国军. 带饱和执行器的线性系统的鲁棒控制研究[D]. 杭州: 浙江工业大学, 2003.

[ 6 ]SONTAG E D, SUSSMANN H J. Nonlinear output feedback design for linear systems with saturating controls[C]∥IEEE Control Systems Soc. Proceedings of the Conference on Decision and Control, Honolulu HI USA, 1990:3414-3416.

[ 7 ]张新权. 几类具有执行器饱和的切换系统的分析与综合[D]. 沈阳: 东北大学, 2011.

[ 8 ]李晓银. 具有执行器饱和的非线性切换系统的优化与控制研究[D]. 阜新: 辽宁工程技术大学, 2012.

[ 9 ]YUAN C Z, WU F. Switching control of linear systems subject to asymmetric actuator saturation[J]. International Journal of Control, 2015,881:424-451.

[10]DUAN C, WU F. New results on switched linear systems with actuator saturation[J]. International Journal of Systems Science, 2016,475:276-289.

[11]周丽明. 饱和控制系统理论及应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[12]俞立. 鲁棒控制线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.

[13]ZUO Z Q, Wang Y J, On enlarging the domain of attraction for linear systems subject to actuator saturation[J]. International Journal of General Systems, 2008,37(2):239-248.

[14]赵克友,魏爱荣. 执行器饱和线性系统的镇定性[C]. 2005中国控制与决策学术年会, 沈阳2005:102-104.

[15]马东星. 饱和系统的稳定性分析与抗饱和控制[D]. 杭州: 浙江大学, 2006.

[16]吕亮. 具有执行器饱和的控制系统分析与设计[D]. 上海: 上海交通大学, 2010.

[17]沈凡杰. 具有饱和执行器系统的控制方法研究[D]. 沈阳: 沈阳师范大学, 2016.

Control of switched systems with actuator saturation

JING Li1, DONG Qiuyang2

(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

In this paper, we study a class of switched systems with actuator saturation. We mainly explore the stability criterion of the system when actuator saturation exists, and prove the conclusion. Firstly, how to dispose saturation is very important. We dispose saturation by using the sector region method. Secondly, according to the Lyapunov theory, the paper gets the stability criterion. Thirdly, the paper turns the criterion into the inequality in order to solve the problem by LMI tools in Matlab. Finally, the paper estimates the attraction domain of the system. It also provides a numerical example to demonstrate that the conclusion in this paper is effective and feasible.

switched system; actuator saturation; Lyapunov theorem; linear matrix inequality

1673-5862(2017)02-0151-05

2017-05-10。

辽宁省教育厅科学研究一般项目(L2014435)。

景 丽(1967-),女,辽宁沈阳人,沈阳师范大学副教授,博士。

O436

A

10.3969/ j.issn.1673-5862.2017.02.005