基于粒子滤波的短时正弦信号相位参数估计

2017-06-07邹学玉袁延秀熊杰

长江大学学报(自科版) 2017年9期

关键词：参数估计正弦信噪比

邹学玉，袁延秀，熊杰

(长江大学电子信息学院，湖北荆州 434023)

基于粒子滤波的短时正弦信号相位参数估计

邹学玉，袁延秀，熊杰

(长江大学电子信息学院，湖北荆州 434023)

针对传统的相位参数估计方法的精度和局部收敛问题，提出了一种基于粒子滤波算法估计短时正弦信号相位的方法，设计了算法流程，研究了粒子数和相似度对参数估计精度的影响，估计了不同信噪比的正弦信号的相位，并与遗传算法和最小二乘法的结果进行了比较分析。结果表明，在信噪比大于20dB时，粒子滤波算法可以更快速、准确地估计出正弦信号的相位。

粒子滤波；正弦信号；参数估计；相似度

正弦信号的相位参数估计问题不仅在信号处理和通信领域中起着重要的作用，而且在电子、雷达、生物医学、油井射孔等领域也有着重要的作用[1，2]。由于在实际情况下，信号中往往含有噪声，因此，如何高精度地估计含噪声的正弦信号的参数就成为研究的重要内容。利用传统的最小二乘法估计正弦信号的参数时，往往将非线性问题转化为线性问题来处理，但处理过程中存在以下问题[3]：在实践中只有小部分问题能转化为线性问题；随着估计参数的增加，线性化方法的计算量将会成几何级数增长；精度不高。采用拟牛顿法、遗传算法等非线性优化方法来估计正弦信号的参数存在收敛到局部极小点的缺点[4]。基于叠加的互相关函数估计法不能解决混有谐波的信号[5]，对信号持续时间只有几个周期时的应用场景，将无法通过叠加处理增加信噪比，如基于TCP的油井射孔起爆时点分析等效为起爆信号的相位分析[2,6]。由于油井射孔震动信号持续时间只有几个周期，因此，笔者给出了一种基于粒子滤波算法[7]的短时正弦信号的相位估计法，并应用于测试数据处理中。由于粒子滤波算法的收敛性好，因此能够精确地估计短时正弦信号的相位参数。给出了利用该方法估计含不同信噪比的短时正弦信号的相位的结果，并与遗传算法和最小二乘法的结果作了分析比较。

1 标准粒子滤波算法

粒子滤波是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法，它依据大数定理，采用蒙特卡罗方法来求解贝叶斯估计中的积分运算[8]。其基本思想是先根据系统的状态向量的经验条件分布在状态空间产生一组随机样本的集合，这些样本就是所谓的粒子，再依据测量不断地调整粒子的位置和权重，然后按照调整后的粒子的信息来校正最初的经验条件的分布。简单地说，该算法的主要思想是使用一个含有权值的粒子集合来表示系统的后验概率密度，是一种顺序重要性采样法。当样本容量趋近于无限大时，可以逼近任何形式的概率密度分布。

粒子滤波算法适用于任何可以用状态空间模型来表示的非高斯背景下的非线性随机系统，使预测的粒子接近于真实状态，并且算法的精度可以逼近于最优估计，是一种非常有效的非线性滤波技术。粒子滤波算法在非线性、非高斯方面的优点决定了其广泛的应用范围：在经济学领域常用于预测经济数据；在军事领域常用于雷达跟踪物体；在交通管制领域常用于视频监控。此外，它还用于机器人的定位、故障预测等。

x0：k=f(x0：k-1，uk,wk)

(1)

观测方程为:

y1：k=h(x0：k,ek)

(2)

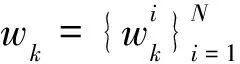
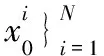
(v)时刻k=k+1,转到(ii)。

2 算法实现

按照标准粒子滤波算法更新权值时，经过几步递归后，可能使粒子的权重集中到少数的粒子上，会导致粒子集无法表示实际的后验概率分布，出现算法退化问题[8]。因此，笔者在标准粒子滤波算法的基础上，将更新权值的方法修改为相似度计算。

Step1 初始化：

(i)确定目标，令endcond=ε，ε是一个趋近于0的正数，迭代轮数turn=1；

Step2 计算相似度：

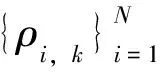
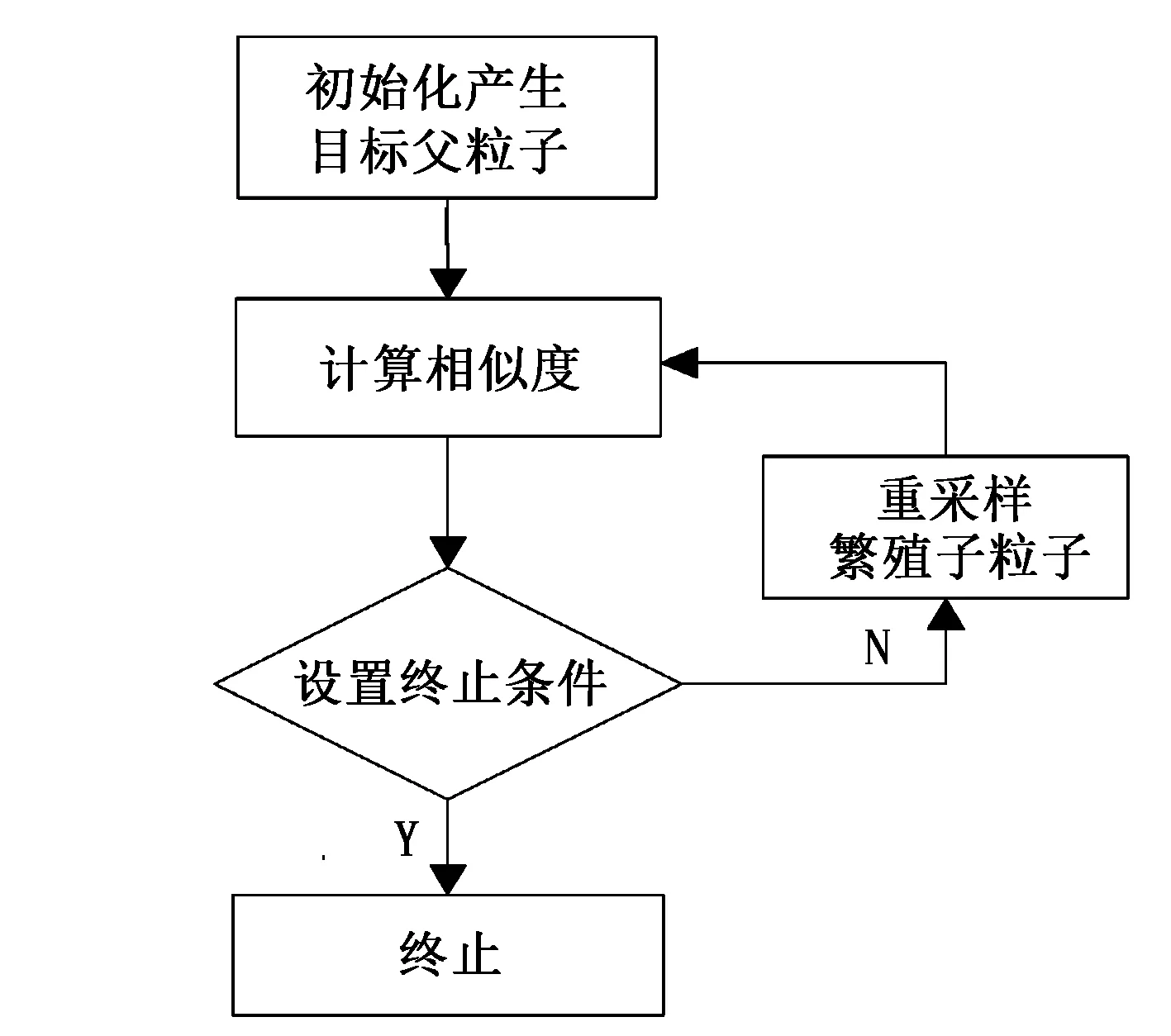
图1 算法主程序流程图

Step3 判断：

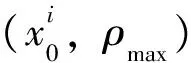
Else 开始重采样。

Step4 重采样：

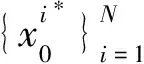
算法的主程序的流程如图1所示。

3 算法中的几个相关问题

1)初代父粒子数目的选择从理论上分析，数目太少会导

致计算结果不精确，数目太多会导致计算量大，因此结合理论分析与试验研究，确定合适的粒子数目。

2)相似度的计算常用的相似度的计算方法有以下3种：

①欧几里德距离[9]。假设x、y是n维空间中的2个点，此时它们之间的欧几里德计算公式为：

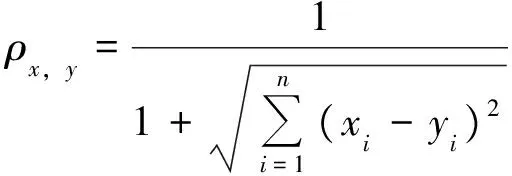
该方法是所有相似度计算里面最简单，但其侧重于距离。

②皮尔森相关系数。皮尔森相关系数表达2个变量之间线性关系的强弱[10]，等于2个变量的协方差除于2个变量X、Y的标准差，用数学公式表示为：

该方法没有考虑重叠的评分项数量对相似度的影响。

③余弦相似度[11]。余弦相似度用向量空间中2个向量夹角的余弦值作为衡量2个个体差异的大小，即：

相比于距离度量，余弦相似度更加注重2个向量在方向上的差异。由于计算粒子与目标的相似度时，不仅要计算两者之间大小的相似度，还要考虑两者之间的方向，因此笔者选择余弦相似度计算粒子与目标之间的相似度。

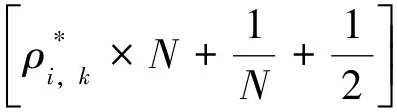
4 测试目标

正弦信号是在工程测试过程中经常遇到的一种信号，其参数包含信号的幅值、频率、相位。任何复杂信号几乎都可以通过傅里叶变换分解为许多频率与幅值均不相同的正弦信号的叠加。这里以有噪正弦信号的相位为测试目标，形式如下：

X(t)=Asin(ωt+θ)+no(t)

(3)

5 结果与分析

5.1 粒子数对相位估值精度的影响

表1为选择不同的粒子数目在不同的噪声下仿真试验得出的相位估计的均值、标准差和绝对误差。由表1中的数据可知，粒子数目选为64时得到的估计结果相对较好。

表1 不同粒子数目在不同噪声下得到的相位估值

5.2 目标估值的精度与速度分析

依据表1的分析结果，设定粒子数N=64，对不同信噪比的目标估值的速度与精度进行分析，结果如表2所示，并且与遗传算法(见表3[13])、最小二乘法(见表4[13])的估值进行比较。

1)估值精度比较分析表2和表3可知，在相同信噪比情况下，粒子滤波算法得到相位估值比遗传算法更接近真实值，标准差更小，当信噪比为20dB时，其精度比遗传算法的精度提高了13.4%。比较分析表2和表4可知，在相同信噪比情况下，粒子滤波算法的估值精度显著优于较传统最小二乘法的估值精度。

表2 粒子滤波算法仿真计算结果

表3 遗传算法仿真计算结果

2)估值速度分析表2可知，随着信噪比的提高，粒子滤波估值迭代次数显著减少。并且与文献[13]的遗传算法迭代次数相比(见表3)，在信噪比为60dB时，粒子滤波算法的速度比遗传算法的速度提高了2.25倍。

表4 最小二乘法仿真计算结果

综合表2、表3[13]、表4[13]数据结果与分析可知，当信噪比大于20dB时，相对于遗传算法和最小二乘法，粒子滤波算法不仅精度高、速度快、而且得到的估值比较稳定、收敛性好。大量的仿真结果表明，当信噪比大于40dB时，粒子滤波算法能够快速、稳定地估计出目标值。

6 结语

笔者提出的基于粒子滤波算法的短时正弦信号相位估计方法，同样也可用来估计信号的幅值和频率，以及类似正弦信号的特征参数。从本质上看，正弦信号参数估计实际上是一高度非线性的优化问题，由于粒子滤波算法是一类全局收敛算法，因此所得到的正弦信号参数估计结果也是全局最优解，不仅克服了传统参数估计方法的局部收敛问题，而且比已有的遗传算法和最小二乘法的估值的精度高、速度快，该短时信号参数估计具有良好的实时性，并将应用于油气井射孔信号的处理与分析中。在试验研究中发现，随着短时信号信噪比降低，参数估计误差逐渐变大，因此对提高低信噪比信号参数估计精度也将是下一步要开展的工作。

[1]何俊发. 强噪声背景下微弱正弦信号参数估计算法研究[D]. 哈尔滨：哈尔滨工程大学,2013.

[2]刘贯虹.油管输送射孔(TCP) 监测识别系统[J].测井技术，2008,32(2):128～133

[3]芦文波,韩韬,施文康,等. 提取正弦信号参数的非线性寻优最小二乘算法[J]. 上海交通大学学报,2003，37(10):1613～1615.

[4]袁亚湘,孙文瑜. 最优化理论与方法[M]. 北京:科学出版社，1997.

[5]张晓威,孟凡明. 正弦信号幅值和初相位估计的问题研究[J]. 计算机工程与应用,2013，49(5):216～219.

[6] 柴晓兵.TCP起爆监测识别系统在SKS3000射孔测井仪中的应用[J]. 国外测井技术,2011(3):66～68.

[7]胡士强,敬忠良. 粒子滤波原理及其应用[M]. 北京:科学出版社，2010.

[8]朱志宇. 粒子滤波算法及其应用[M]. 北京：科学出版社，2010.

[9]陈汉军,杨雪. 欧几里德距离的几种定义与应用[J]. 天津轻工业学院学报,2003(S1):65～66+78.

[10]王忠玉,吴柏林. 一类模糊数据的相关系数研究[J]. 经济研究导刊,2015(2):248～251.

[11]李巍,孙涛,陈建孝,等. 基于加权余弦相似度的XML文档聚类研究[J]. 吉林大学学报(信息科学版), 2010(1):68～76.

[12]Rubin D. Using the SIR algorithm to simulate the posterior distribution[J]. In Bayesian Statistics, 1988(3):395～402.