学习活动指数LAI及在线学习活动指数OLAI的具体分析

贾积有+于悦洋

【摘 要】

本研究提出了一个描绘学生学习活动的指数LAI（Learning Activity Index）及其在线形式——在线学习活动指数OLAI（Online Learning Activity Index）。学生完成某次学习活动的好坏，可以从速度（speed）、质量（quality）和数量（quantity）三个维度进行综合评判。本研究将这三个方面进行数字化处理，得到三个独立的无量纲指标，而学习活动指数LAI就等于这三个维度指标之和。在某个学习段内，每个学生的LAI均值反映了该生参与课程活动的平均表现，而LAI之和则反映了参与课程活动的总体表现。同理，某个学生群体（如班级和学校等）的学习活动指数LAI也可以平均和求和，分别反映全体学生的平均表现和总体表现。在线学习活动指数OLAI则可以刻画在线学习活动的好坏。基于这样的定义，本研究对一个在线数学学习平台“乐学一百”上部分学生的学习活动数据进行了深度挖掘，计算出了每个学生的OLAI三个维度以及OLAI的数值，发现在教师带领下进行混合式学习的6个班级学生的OLAI及其三个维度的数值的离散程度显著低于其他自由学习的学生，完成活动的平均速度也较快。将这些数值与学生在常规考试中的成绩进行相关和回归分析后，本研究发现学生成绩与在线学习活动指数OLAI有较强的正相关关系，或者说在线学习活动指数OLAI可以较好地预测学生的学业成绩。因此，本研究建议学习活动平台或者课程管理平台设计开发者可以将在线学习活动指数OLAI嵌入平台设计，学校、教师和家长也可以将其作为个性化教学的一个基础指标来看待。该指标对于学习分析研究具有重要的理论和实践指导意义。

【关键词】 学习分析；学习活动；在线学习活动；学习活动指数LAI；在线学习活动指数OLAI

【中图分类号】 G642 【文献标识码】 A 【文章编号】 1009-458x（2017）04-0015-09

一、概念界定

关于在线学习活动分析，近年来随着在线学习、慕课等的兴起而成为国内外研究的热点问题之一（王萍， 2015； Elbadrawy， Polyzou， Ren， Sweeney， Karypis， & Rangwala， 2016； Moissa， Gasparini， & Kemczinski， 2015）。然而，到底什么是学习活动和在线学习活动，国内外文献并没有明确的定义。在常规教学环境下，学生参加的学习活动包括课前、课上和课后三个部分。课前活动包括预习活动，如阅读课本内容和尝试做题等；课上活动包括听讲、思考、回答问题、参与讨论、参加课堂练习以及各个阶段考试等；课后活动包括完成各种作业、复习课本内容等。

在线学习活动是指学习者在某个学习平台或者课程管理系统上学习时参与的活动，包括阅读课程网页、观看课程视频、在线做题、讨论发帖或者回帖、提交作业、同伴互评等。在这些活动中，在线做题是非常重要的一类活动，也是大多数网络教学平台都支持的一种学习活动。在线做题的类型包括选择题和填空题等客观题，这些客观题可以预设标准答案。当学生提交回答后，系统自动判断其正确程度、给出得分和相应的反馈。一般来说，学习平台或者课程管理系统都会记录、保存用户提交的每道題的答案、所用时间、尝试次数等详细数据，这些数据构成了对学生学习活动进行深度挖掘的基础信息。

二、相关研究

基于学生学习活动的学习分析已经成为涉及多个领域的一项前沿、交叉学科（包昊罡， 李艳燕，2015； 李艳燕， 马韶茜， 黄荣怀，2012）。很多学者探讨了学习分析的教育意义、重要性、必要性、技术和系统框架等（顾小清， 张进良， 蔡慧英， 2012； 赵艳， 赵蔚， 姜强， 2014； 贺超凯， 吴蒙， 2016； 郑旭东， 杨九民， 2016）。魏顺平（2011）针对Moodle平台数据，通过常规统计方法、可视化方法、聚类方法、社会网络分析方法等，对网络学习平台的日志和交互论坛数据进行数据挖掘，揭示出某一网络培训班在线学习过程中师生活动的总体情况，发现学生的模块访问偏好和学习时间偏好，分析得出师生交互网络的结构特点。魏顺平 （2012）以中央电大开放教育入门课程“开放教育学习指南”网络课程为例，以2010 年春季学期江苏电大9，369名新生学习该课程时所产生的登录数据、资源浏览数据和形成性考核数据为分析对象，采用数据挖掘方法得出登录、资源浏览、作业、测试等在线学习活动的特点及其影响因素。贾积有等（2014）对COURSERA上北大6门慕课的数据进行了详细分析，试图发现课程层面上学员的网上学习活动及其对学业成绩的影响。相关分析结果表明，学业成绩与平时测验成绩和论坛活跃程度（发帖、回帖）有比较强烈的正相关关系，与观看课程网页次数有一定的正相关关系。

遗憾的是，目前国内外文献还缺少定量描述学生在线学习活动的方法和指标的研究。这也是开展本研究的重要原因。

三、评价学习活动的三个维度

教师习惯上从“多、快、好”三个维度评价学生完成活动的好坏。“多”代表完成活动的数量，“快”代表完成活动的速度，“好”代表完成活动的质量。比如做作业题，如果做的题多、速度快、正确率高（比如百分之百地正确），那么学生的得分自然就高。

如果能将这三个维度（数量、质量和速度）都数量化，然后将三者合并到一起，成为一个量化的学习活动指数LAI（Learning Activity Index），就可以使用它来描述学生的学习活动了。就像人们常用BMI来衡量人体胖瘦程度以及是否健康一样。

传统教学方式支撑的学习活动，学生参与活动的质量维度可以通过教师评判的得分、级别等进行度量，数量维度也容易通过活动内容数量（如题目多少）来度量，但是每个学生完成活动的速度或者说参与活动的时间却较难准确地测量并记录下来。

在线学习平台或者课程管理系统支持的学习活动，通常会记录学生完成某个活动的起始和结束时间，可以由此计算完成该活动的速度，也会记录完成活动的质量（比如对客观题目的自动评分、对主观题目的教师判分或者同伴互评得分等）和数量。所以，可以计算在线学习活动指数OLAI（Online Learning Activity Index）。下面就以一个在线数学学习平台“乐学一百”为例，介绍OLAI的计算公式和用途。

四、基于“乐学一百”系统定义

在线学习活动指数OLAI

（一）“乐学一百”系统学习数据描述

北京乐学一百在线教育科技有限公司总结近15年多媒体教育软件及混合式教学实践经验，研发了“乐学一百”在线教学系统。该系统聚焦中小学数学教学，包括与全国初中和小学数学大部分通用教材相配套的习题内容，全部为自己研发。在该系统上，学生的学习活动主要是闯关做题，每道关卡对应一套包含若干道题的测验题，题型为选择题或者填空题。学生必须依次做对每道题（不管做多少次），才算闯关成功。系统会生成一条记录，主要包括的信息有：学生做该套题的时间（usetime，单位为秒），相对于标准时间（系统通过测算给出的一个完成题目的合适时间量）的提前或者推迟时间（difference，提前为正值，推迟为负值，单位为秒），包含每道题尝试答案的做题过程数据（Result），等等。

对每套题的做题过程数据（result）进行详细分析，可以得到学生在做每套题中的如下信息：题个数（question_number）；错题次数（wrongs），即不是第一次就做对的题的个数；尝试次数（tries），即做错题的尝试次数之和；猜测做对的题次数（guesses，假设猜测4次及以上就为一次猜测做题，而不是真正思考推理得出的答案）。

（二）速度维度Speed的定义

基于以上学习活动信息，本研究定义学生在线学习指数OLAI的速度维度speed为：

speed=difference/（usetime+difference）

它代表相对标准时间（usetime+ difference）的偏离值，反映了学生做题的快慢，即速率。

例如，一套题的标准完成时间为100秒：

若usetime=33，difference=67，则

Speed1=67/（33+67）=67/100=0.67

若usetime=89，difference=11，则

Speed2=11/（89+11）=11/100=0.11

若usetime=100，difference=0，则

speed3=0

若usetime=150，difference=-50，则

speed4=-50/（150-50）=-50/100=-0.5

若usetime=200，difference=-100，则

Speed5=-100/（200-100）=-100/100=-1

显然，这五个速度相比，speed1>speed2>speed3>speed4>speed5。

按照这样的定义，speed值越大，表明该学生做这套题的时间越短，速度越快。当usetime=0时，speed达到最大值1，也就是说学生没有花费时间就完成活动了，当然这是极限的理想状态；当usetime为无穷大时，speed为无穷大的负数，表示该生始终没有完成该活动，当然这是极限的最差状态。如果speed=0，则表示该学生的速度属于标准水平；如果speed>0，则表示该学生做题速度较快；如果speed<0，则表示该学生做题速度较慢。比如，Speed5=-1，表示该学生花了两倍于标准时间的时间来完成一套题，效率较低。当speed为负数并且绝对值越大，表示完成这套题花费时间越多，说明学生在做题过程中可能三心二意或者暂时中断去做别的事情了。

（三）质量维度Quality的定义

因为学生可以多次尝试每道题的答案，直到正确才能通过该套题构成的关卡，因此，本研究定义这套题的做题质量，也就是准确率quality为：

quality=（question_number-guesses）/（question_number+tries）

其中，分子部分question_number-guesses，表示學生不是通过猜测做对的题数量；本研究没有采用question_number-wrongs （其数值小于question_number-guesses，因为guesses

例如，若一个关卡（即一套题）包含了10道题，即question_number=10：

若guesses=0，tries=10，则quality=10 /（10+10）=0.5。就是说，在这10道题的做题过程中，没有一道题尝试次数大于3，但至少有4道题都没有一次做对，全套题的准确率为50%。

若guesses=1，tries=5，则quality=（10-1）/（10+5）=0.6。就是说，在这10道题的做题过程中，有一道题尝试次数大于3，即为猜测出来的，但是还有一道题是尝试一次就做对了，全套题的准确率为60%。

若tries=0，guesses=0，则quality=1，这是最好的做题结果，就是一次做对了全部（100%）题。

若guesses=question_number，quality=0，这是最差的做题结果，表示没有一道题是尝试4次以下做出来的。

所以quality是一个介于0到1之间的正数，数值越大表明做题准确率越高、质量越好。

（四）数量维度Quantity的定义

本研究定义学生做这一套题的数量quantity为：

quantity=Question_number/Standard_number

其中，Standard_number为系统平台在所研究时间范围内学生能够在短于标准时间的时间内（difference>=0）一次答对（quality=100%）的题数量的均值，为26.7。这个取值同时考虑了学生的做题数量范围和所花费时间两个因素。当然，该标准值也可以由学科教学专家人为定义。

显然quantity>0，并且数值越大，表明学生在系统平台已经完成的题数量越多。

（五）在线学习活动指数OLAI的定义

考虑到speed， quality和quantity都是无量纲的实数，本研究定义学生在某次做题中的在线学习活动指数OLAI为：

OLAI= speed +quality+ quantity

因为speed可以为负值且最大值为1，quality介于0到1之间，quantity为正值且最小值为0，所以理论上OLAI的最大、最小值均可能取到无限。但是，因为当一门课程的题数量确定后，quantity对于所有做题的学生都是相同的，所以OLAI的范围并非无限大。OLAI的数值越大，则这次做题的结果越好，也就是说学生越快、越好地完成了这套题，这正是我们教学所期待的结果！更加细致地分析OLAI三个维度数值范围，还可以看到其对应的教学意义，如表1所示。

如果某个学生重复多次做了同一套题，考虑到鼓励学生“越试越好，越战越勇”的教学策略，则可以根据常见的“多次考试，取最好成绩”的评价原则，取多次OLAI值中最大值作为该学生在该套题上的学习活动指数OLAI。当然，如果采用其他教学策略，也可以根据需要取多次OLAI的平均值。

根据某个学生每次做题情况算出OLAI，并以此为纵坐标，同时以时间为横坐标做散点图或者折线图，就可以看出这个学生学习活动指数随时间发展的趋势和走向。

將某个学生在某个学期或某个时间段内所有活动的OLAI求平均，即为该学生的平均学习活动指数OLAIMAA（OLAI Mean of All Activities），它可以反映该学生所有活动的平均表现。三个维度的相应均值分别反映了该学生所有活动的平均速度、平均质量和平均数量。

将某个学生在某个学期或者某个时间段内参加所有活动的OLAI值求和，即为该学生的学习活动指数总值OLAISAA（OLAI Sum of All Activities），它可以反映该学生的学习活动总体表现。三个维度（速度、数量和质量）的相应总值分别反映了该学生所有活动的三个维度的总体表现。

将某个班级、某个学校或者某类学生的在线学习活动指数均值OLAIMAA再求平均，则得到该群体全体学生在线学习活动指数均值OLAIMAAAP（OLAI Mean of All Activities of All Participants），它可以反映该群体学生所有活动的平均表现。

将某个班级、某个学校或者某类学生的在线学习活动指数总值OLAISAA再求和，则得到该群体全体学生在线学习活动指数总值OLAISAAAP（OLAI Sum of All Activities of All Participants），它反映了该群体所有学生所有活动的总体表现。

一个学生的学习活动指数可以和班级的平均值相比，也可以与表1中的绝对标准相比。每次活动以后，系统可以让学生看到该次活动的行为指数和三个维度的数值，还可以基于这些数值授予学生一定的积分或者虚拟货币之类的奖励。

所以，学习活动指数不仅可以衡量一个学生个体在某次活动中的表现，还可以衡量该个体的平均表现和总体表现，也可以刻画一个学校和一个班级的所有学生的学习活动表现的平均值和总体表现。

这样定义的在线学生学习活动指标，不仅可以用于本文作为案例的“乐学一百”平台，也可以用于其他类型的学习系统或者课程管理系统，还可以刻画常规学习中的学习活动，是一个衡量学生学习活动的普适指标。

五、“乐学一百”系统在线学习

活动指数OLAI计算和分析

本研究分析了从2013年1月15日到2016年8月1日的部分平台数据，用户包括来自5所学校6个班级的参与“乐学一百、智能教育”课题的学生，和其他没有参加这个课题研究的学生，即自由用户。这6个班级（代号分别为LX5、LX4、SJS、YF、ZB和QYD）的学生在教师带领下进行混合式学习，即将平台上的练习与常规课堂学习结合起来。作为自由用户的学生则没有学校教师的指导，而是根据自己的需求使用系统。

（一）全体学生和6个班级的在线学习活动指数OLAI统计

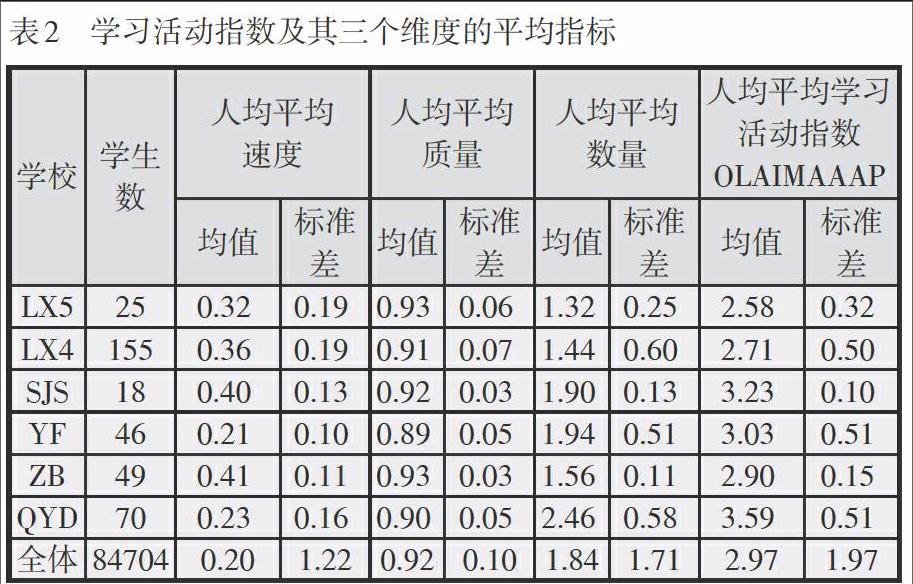
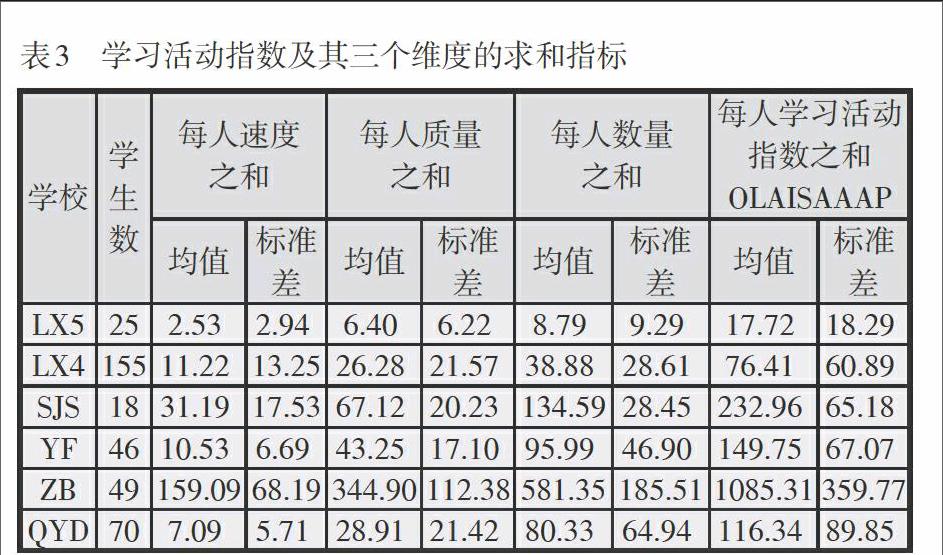
按照前面的定义，本研究计算了全体学生的平均学习活动指数（OLAIMAA）的人均数值（OLAIMAAAP）及其三个维度人均数值的均值和标准差，也计算了6个班级的相关统计量，结果如表2所示。然后，计算了6个班级的学习活动指数总值（OLAISAA）的人均均值（OLAISAAAP）及其三个维度求和后的相关统计量，结果如表3所示。

从表2可以看出，从平均指标上看，无论是OLAI总值还是各个分量，这6个班级之间的差别不大。而从平均指标的离散程度上看，ZB的标准差最小，LX4和LX5的标准差相对均值而言较大，说明这两个班级的学生每次做题情况的差别较大。

因为这6个班级的总学生数占全体用户数的比例只有0.4%，而这6个班级的OLAI值及其各个维度的平均指标与全体用户的各个指标差别不大，除了后者平均速度略低，所以除去这6个班级之外的自由用户群体的OLAI值及其各个维度的平均指标与这6个班级的差别也不大，只是平均速度略低。但是，在平均指标的离散程度上，这6个班级的OLAI及其各个维度的标准差显著低于其他用户，说明在教师指导下进行混合式学习的学生的活动完成程度的离散程度较小，内部差异不大，而其他无教师指导的自由用户之间的活动表现差异很大。

从表3可以看出，在累积或者汇总指标上，无论在OLAI总值还是各个分量上，这6个班级的差别都较大。考虑到ZB使用平台时间为两个学期，而其他学校为1个学期，所以ZB的OLAI总值和各个分量很大是可以理解的。从离散程度上而言，LX4和LX5的标准差很大，表明学生在总体参与程度上差别较大。

（二）全体学生全体做题记录OLAI与三个分量之间的关系

根据系统记录的5，277，251条做题记录，计算出每次做题的学习活动指数OLAI及其三个维度的数值，然后计算出这四个数值之间的相关系数。结果表明，学生做题的速度维度与质量维度之间有较弱的正相关关系（相关系数=0.15），与数量维度有较弱的负相关关系（相关系数=-0.15）；学生做题的质量维度与数量维度基本无相关关系（相关系数=-0.03）。因为数量维度的数值较大，对OLAI的贡献比例最大，所以数量维度与OLAI之间有比较明显的正相关关系（相关系数=0.8）。

因为有些题被某些学生做了多次，本研究采用了取最大值的办法，统计出每个测试被某个学生多次所做取得的在线学习活动指数OLAI最大值及其三个维度的数值。这样得到3，307，177条记录，然后计算这四个数值之间的相关系数。结果表明，学生做题的速度维度与质量维度之间有一定的正相关关系（相关系数=0.25），与数量维度有一定的负相关关系（相关系数=-0.34）；题目质量维度与数量维度基本无相关关系（相关系数=-0.07）。因为数量维度的数值较大，对OLAI的贡献比例最大，所以数量维度与OLAI之间有比较明显的正相关关系（相关系数=0.96）。

进一步计算每个学生OLAI均值（OLAIMAA）及其各个维度的数值，得到84，704条记录。分析它们之间的相关系数，结果表明，速度维度与质量维度之间有一定的正相关关系（相关系数=0.27），与数量维度有一定的负相关关系（相关系数=-0.3）；题的质量维度与数量维度基本无相关关系（相关系数=-0.09）。因为数量维度的数值较大，对OLAI的贡献比例最大，所以数量维度与OLAI之间有比较明显的正相关关系（相关系数=0.93）。

再计算出每个学生的OLAI总值（OLAISAA）及其各个分量的数值，得到84，704条记录；分析它们之间的相关系数，结果如表4所示。四者相互之间具有较强的正相关关系。可见，从学生一个学期或者更长时间的整体表现来看，速度维度、质量维度和数量维度之间是密切相关的，即做题数量越多，速度越快，质量越高。

（三）全体学生学习活动指数三个分量之和的聚类分析

本研究基于每个学生学习活动指数三个分量之和，采用WEKA的聚类功能，将84，704个学生分为六类。如表5所示。

从表5可见，类2为最好的一类，质量接近1，速度和数量都很高，占比11%；类5次之，占比8%；类1为最差的一类，占比最大为28%；类4、类3、类0的表现逐渐变好。

聚类结果的散点图之一如图1所示，横轴为速度，纵轴为质量。速度分布比较集中，而质量差别基本上就是不同类别的主要差距所在。

六、在线学习活动指数OLAI与

其维度之间的相关性分析

学生的学习活动指数考虑了学生做题的速度、质量和数量。那么，它与学生在常规考试中的成绩有无关系呢？

如果学生的常规考试成绩与学生平时在线做题的速度、质量和数量成正相关关系，那么也与三者的合成指标——学习活动指数OLAI成正相关关系。按照这个思路，在对6个班级使用平台后最后一次期末考试成绩与平台OLAI及其各个分量做相关分析和回归分析之前，本研究先分析这6个班级学生学习活动指数OLAI与三个维度数值之间的相关性。

根据系统记录的403，033条做题记录，计算出每次做题的学习活动指数OLAI及其三个维度的数值，然后计算出这四个数值之间的相关系数。结果表明，速度维度与质量维度之间有较弱的正相关关系（相关系数=0.28），与数量维度有一定的负相关关系（相关系数=-0.46）。题目质量维度和数量维度之间具有较弱的负相关关系（相关系数=-0.23）。因为数量维度的数值较大，对OLAI的贡献比例最大，所以数量维度与OLAI之间有比较明显的正相关关系（相关系数=0.78）。这点与全体平台数据分析结果一致。

因为有些套题被某些学生做了多次，本研究采用了取最大值的办法，统计出每一套题被某个学生多次所做取得的在线学习活动指数OLAI最大值及其三个维度的数值。这样得到29，071条记录，然后计算出这四个数值之间的相关系数。结果表明，速度维度与质量维度之间有一定的正相关关系（相关系数=0.3），与数量维度有一定的负相关关系（相关系数=-0.44）。数量维度与质量维度之间具有较弱的负相关关系（相关系数=-0.11）。因为数量维度的数值较大，对OLAI的贡献比例最大，所以数量维度与OLAI之间有比较明显的正相关关系（相关系数=0.95）。这点与全体学生数据分析结果一致。

再计算出每个学生OLAI均值（OLAIMAA）及其各个维度的均值，得到376条记录，分析它们之间的相关系数。结果表明，速度维度与质量维度之间有一定的正相关关系（相关系数=0.37），与数量维度有一定的负相关关系（相关系数=-0.56）；题的质量维度与数量维度具有较弱的负相关关系（相关系数=-0.21）。原因可能是通过题的数量较多的单元测验套题时，学生的速度和质量会下降。因为数量维度的数值较大，对OLAI的贡献比例最大，所以数量维度与OLAI之间有比较明显的正相关关系（相关系数=0.95）。

再计算出每个学生的OLAI总值（OLAISAA）及其各个维度分别的和，得到376条记录，分析它們之间的相关系数，如表6所示。

四者相互之间显示出很强的正相关关系。可见，从学生一个学期或者更长时间的整体表现来看，速度、质量和数量之间是密切正相关的，即做题越多，速度越快，质量越高。

七、在线学习活动指数OLAI及其维度与

学生期末成绩的回归分析

基于上述结论，本研究通过回归分析，详细考察了在线学习活动指数OLAI及其维度的均值、总和与学生期末考试成绩的关系。

将OLAI三个维度的均值作为自变量，分析其对期末考试成绩的影响，结果显示6个班级中的2个（LX4和YF）期末成绩与三个维度的均值都呈现显著正相关，2个（LX5和SJS）期末成绩与三个维度的均值都未呈现显著的相关性，2个（ZB和QYD）期末成绩与质量均值呈现显著的正相关性。所以，在速度、质量和数量某一方面单独表现很好，即使是平均而言，并不能对考试成绩的提高做出显著贡献。

將OLAI三个维度的总和作为自变量，分析其对期末考试成绩的影响，结果显示6个班级中的4个（ZB、SJS、YF和LX5）期末成绩与三个维度的求和都未呈现显著的相关性，1个（QYD）期末成绩与速度总和呈现显著的负相关性，只有一个（LX4）期末成绩与速度求和与数量求和显著正相关，但与质量求和显著负相关。所以，总体而言，速度、质量和数量某一方面单独表现很好，即使是较长时期的表现，也并不能对考试成绩的提高做出显著贡献。

将OLAI均值作为自变量，分析其对期末考试成绩的影响，结果显示6个班级中的4个（ZB、QYD、YF和LX4）期末成绩与OLAI均值呈现显著的正相关性，1个（SJS）呈现显著的负相关性，1个（LX5）无显著相关性。

将OLAI总和作为自变量，分析其对期末考试成绩的影响，结果显示6个班级中的4个（ZB、QYD、YF、LX4）期末成绩与OLAI总值呈现显著正相关性，2个（SJS和LX5）无显著相关性。

将OLAI均值和总和作为自变量的分析结果一致之处是：6个班级中的4个（ZB、QYD、YF、LX4）期末成绩与OLAI均值或者总值呈现显著的正相关性，2个（SJS和LX5）无显著相关性或者呈现显著的负相关性。不过，这2个未显示相关性或者呈现显著的负相关性的班级学生数量是6个班级之中最少的，分别为SJS18个、LX525个。

综上所述，回归分析表明，在比较大的样本中，学生通过平台学习后，在常规考试中的期末成绩与在线学习活动指数OLAI的均值和总值呈现显著的正相关性。

八、学习活动指数LAI的理论和实践意义

本研究提出了一个描绘学生学习活动的指数LAI，及其在线形式——在线学习活动指数OLAI。学生完成某次学习活动的好坏，可以从速度、质量和数量三个维度进行综合评判。对于在线学习活动指数OLAI，本研究将它的三个维度进行了具体定义，得到三个独立的无量纲指标，学习活动指数LAI就等于这三个维度指标之和。在某个学习段内，每个学生的LAI均值反映了该学生参与课程活动的平均表现，而LAI之和则反映了参与课程活动的总体表现。同理，某个学生群体（如班级和学校等）的学习活动指数LAI也可以平均和求和，分别反映全体学生的平均表现和总体表现。在线学习活动指数OLAI则可以描述在线学习活动的好坏。

基于这样的定义，本研究对一个在线数学学习平台“乐学一百”上的部分用户的学习活动数据进行了深度挖掘，计算出了每个学生的OLAI三个维度的数值以及OLAI的数值，并进一步单独计算了6个使用该平台进行混合式学习的班级的学生OLAI数值，发现这些数据可以较好地反映学生的学习情况。本研究将这些数值与学生期末成绩进行了相关和回归分析，发现学生成绩与在线学习活动指数OLAI呈较强的正相关关系，或者说在线学习活动指数OLAI可以较好地预测学生的学业成绩；学习活动指数的三个维度（速度、质量和数量）某一方面单独表现即使很好，不管是平均每次还是较长时期的累积表现，都不能对考试成绩的提高做出显著贡献。

基于以上数据挖掘成果，本研究建议学习活动平台或者课程管理平台设计和开发者可以将在线学习活动指数OLAI嵌入平台设计，学校、教师或者家长可以将其作为个性化学习的一个基础指标来看待，以了解学习者的学习进度，并在此基础上因材施教、实施个性化教学。

当然，在基于“乐学一百”平台的学习活动指数分析中，因为在该平台的主要学习活动是测验通关，所以对OLAI三个维度中的质量的定义完全基于测验这种学习活动，而对于速度和数量的定义则适合其他学习活动。同时，对于讨论、同伴互评等其他学习活动，还要结合具体情况给出确切的质量定义，才能计算出质量数值，并与速度和数量的数值相加得出在线学习活动指数的值。不过，因为测验几乎是目前所有学习平台和课程管理系统中都必备的一种教学活动，就像传统教学环境下的测验一样，是一项必不可少的教学活动，所以本研究提出的OLAI三个维度的计算公式具有较为普遍的适用性。

致谢：本研究得到北京乐学一百在线教育科技有限公司委托课题“乐学一百、智能教育”的资助，特此表示感谢！同时也对参与课题研究的全体教师和学生表示诚挚的谢意！

[参考文献]

包昊罡，李艳燕. 2015. 大数据背景下学习分析的特点[J]. 北京广播电视大学学报（01）：9-13.

顾小清，张进良，蔡慧英. 2012. 学习分析：正在浮现中的数据技术[J]. 远程教育杂志（01）：18-25.

贺超凯，吴蒙. 2016. edX平台教育大数据的学习行为分析与预测[J]. 中国远程教育（06）：54-59.

贾积有，缪静敏，汪琼. 2014. MOOC学习行为及效果的大数据分析——以北大6门MOOC为例[J]. 工业和信息化教育（9）：23-29.

李艳燕，马韶茜，黄荣怀. 2012. 学习分析技术：服务学习过程设计和优化[J]. 开放教育研究（05）：18-24.

王萍. 2015. 基于edX开放数据的学习者学习分析[J]. 现代教育技术 （04）：86-93.

魏顺平. 2011. Moodle平台数据挖掘研究——以一门在线培训课程学习过程分析为例[J]. 中国远程教育（01）：24-30.

魏顺平. 2012. 在线学习行为特点及其影响因素分析研究[J]. 开放教育研究（04）：81-90.

赵艳，赵蔚，姜强. 2014. 基于学习分析技术的中小学教师远程培训效果影响因素实证研究[J]. 中国电化教育（09）：132-138.

郑旭东，杨九民. 2016. 学习分析在高等教育领域内的创新应用：进展、挑战与出路[J]. 中国电化教育（02）：2-7.

Elbadrawy， A.， Polyzou， A.， Ren， Z.， Sweeney， M.， Karypis， G.， &Rangwala， H. （2016）. Predicting Student Performance Using Personalized Analytics[J]. IEEE Computer， 49（4）， 61-69.

Hughes， G.， & Dobbins， C. （2015）.The utilization of data analysis techniques in predicting student performance in massive open online courses （MOOCs）[J]. Research and Practice in Technology Enhanced Learning， 10（1）， 10-15.

Moissa， B.， Gasparini， I.， & Kemczinski， A. （2015）. A Systematic Mapping on the Learning Analytics Field and Its Analysis in the Massive Open Online Courses Context[J]. International Journal of Distance Education Technologies， 13（3）， 1-24.

收稿日期：2016-11-20

定稿日期：2016-12-15

作者簡介：贾积有，博士，教授，博士生导师，北京大学教育学院教育技术系，北京大学教育信息化国际研究中心主任（100871）。

于悦洋，北京外国语大学计算机系（100089）。

责任编辑 刘 莉