土地流转背景下缺水地区农用水权初始分配*——基于投影寻踪混沌粒子群优化模型分析

张 雪，郑志来

(盐城师范学院商学院,江苏盐城 224051)

·持续农业·

土地流转背景下缺水地区农用水权初始分配*
——基于投影寻踪混沌粒子群优化模型分析

张 雪，郑志来※

(盐城师范学院商学院,江苏盐城 224051)

[目的]文章从公平性和效率性2个方面选取6个指标构建了缺水地区微观主体农用水权初始分配指标体系，在该指标体系基础上，提出了投影寻踪混沌粒子群优化模型，研究了在土地流转背景下如何对缺水地区微观主体农用水权进行初始分配的问题。[方法]该文利用了投影寻踪技术对微观主体农用水权初始分配问题进行降维处理，采用混沌优化和粒子群优化算法寻找最优投影方向，并通过算例验证分析证明了该模型的可行性、合理性和有效性，为农用水权初始分配问题提供了相应的方法和思路。[结果]研究认为，土地流转使农业生产向土地规模化、经营主体职业化、分工专业化方向发展，为农用水权在微观主体之间进行初始分配提供了条件； 农用初始水权明晰有利于缺水地区优化农业用水结构，节约农业用水，实施农用水权置换，促进农业用水转向第二、三产业，以推动缺水地区产业结构优化升级、社会经济转型发展； 在农用水权初始分配过程中各指标重要性水平不能主观评估，应当由不同地区的样本数据驱动，客观地计算决策方案的最优值，公正地确定权重和水权分配比例。[结论]农用水权初始分配应考虑法律制度政策、社会经济、生态环境等多种因素，以构建完善的农用水权初始分配体系。

微观主体 农用水权分配 投影寻踪 混沌粒子群优化

0 引言

缺水地区经济社会发展面临水资源短缺的约束日益凸显，而农业用水在缺水地区占了很大一部分比重，其中农业灌溉用水又是重中之重。由于我国是传统的农业国家，农村和农产品本身的特殊性决定了我国农业水资源利用存在诸多问题，包括农用水权界定不清、浪费严重、利用效率低下、农民关于水资源属于市场化商品的观念薄弱等。因此，水权制度改革更多地涉及农业方面水权制度； 要从总体上缓解我国缺水问题，必须完善农用水权制度[1]，而农用水权制度的完善则要建立在农用水权初始分配的基础之上。

1 农用水权初始分配研究概述

目前，国内关于水权初始分配的研究取得了一定进展。对于这一领域的研究主要分为两方面：一是从体系、制度设计的层面进行研究； 二是从构建模型的角度研究初始水权如何在某一流域内各地区或某一行政区内各下级行政区之间进行分配，也有研究某一地区初始水权如何在该地区各产业部门(包括农业、工业、第三产业、生态环境以及生活等部门)之间进行分配的。这些研究基本上都是从宏观或者中观层面进行的，专门研究农用水权在微观主体(个体农户或组织)之间如何分配的文献更少。

然而，由于土地流转的不断开展，土地碎片化、农业散户化将逐渐向土地规模化、农业大户化方向转变，农业生产经营将出现农业土地规模化、经营主体职业化、经营方式科学化、农业专业化分工日益明显的趋势[2]。这一趋势的出现将改变实行土地流转地区的农业用水格局，使农业用水主体发生明显变化，这为农用水权在个体农户或组织(以下统称微观主体)之间进行分配提供了必要条件。另一方面，土地流转也为农用水权置换、农业用水向非农转移、水权市场的建立和完善提供了更广阔的空间。而这些体系、制度、市场的完善都要建立在农用初始水权清晰界定的基础上。而我国缺水地区农用初始水权共有范围大部分只界定到县一级，共有规模空间过大，共有范围内农用初始水权界定不清，存在Hardin所证明的“公共地悲剧”，包括农业用水使用量超过最有使用量，浪费严重，节水动力不足； 不同主体之间的水资源过度被挤占，具体表现在主体强势方挤占主体弱势方、上游用户挤占下游用户、耕地用水挤占林草地用水等[2]。因此，在这种形式下，对缺水地区农用水权如何在微观主体之间进行初始分配展开研究就显得尤为重要。

目前，国内外文献关于初始水权分配的研究采用的主要是层次分析法、模糊综合评价法、多目标半结构性模糊优选法、人工神经网络、模糊物元分析法等[3]。这些方法的问题在于要么人为主观地赋予权重构造判断矩阵，要么对样本数据结果或分布特征先作某种假定[3]，在很大程度上存在着主观因素的影响。为了克服这些不足，有文献采用投影寻踪混沌优化算法构造初始水权分配模型[3]，但是混沌优化算法需要迭代的次数过多，寻优速度过慢，在大空间、多变量的优化搜索上存在着计算时间长、不易搜索到最优解的问题。考虑混沌优化算法的不足之处，而粒子群优化算法(CPSO)通用性强、寻优速度快，具有较强全局和局部搜索能力，但是这种方法在收敛速度和摆脱局部最优方面也存在矛盾和不足，可以将混沌优化算法和粒子群优化算法相结合，对现有模型进行改进，以克服二者的不足，发挥二者的优点，构造出有实用价值有特色的混合优化算法。

基于此，文章在前人研究的基础上，利用投影寻踪技术建立农用水权初始分配模型，将混沌优化算法和粒子群优化算法二者的优势结合起来(合称为混沌粒子群优化算法)，提出将投影寻踪混沌粒子群优化模型运用在微观主体农用初始水权分配中，不仅为初始水权分配，也为农用初始水权分配提供了创新的思路和方法。

2 模型假设与构建

2.1 模型假设

为了讨论方便，该文特作如下假设：

第一、由于灌溉用水是农业用水大户，该文只讨论缺水地区农业灌溉用水的初始水权分配问题。

第二、假设农用水权共有范围已界定到县一级，并且用于农业灌溉的用水总量已确定，记作WR。

第三、土地流转使得县域内出现了一定数量规模化的农业生产者，他们使用大面积土地进行农业生产活动。

在此基础上该文讨论农用水权如何在县域内微观主体之间进行分配的问题。

2.2 建立微观主体农用水权初始分配指标体系

该文从农用水权分配的公平性、效率性的原则出发，选取6个指标构建缺水地区微观主体农用水权初始分配指标体系，同时为了体现水权分配的公平性，选取进行水权分配之前的“原实际取水量”作为参考指标，要求进行水权分配后，各微观主体的水权分配量与其有正相关关系，如图1所示。

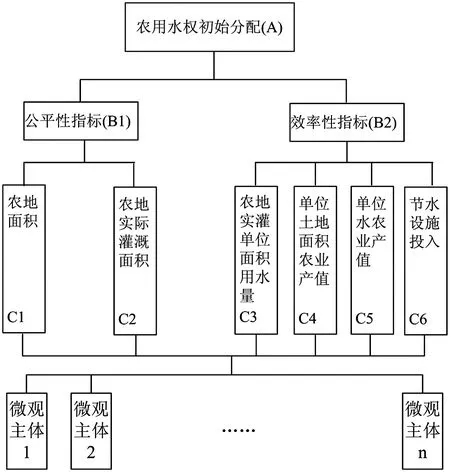
图1 缺水地区农用水权初始分配指标体系

2.2.1 公平性指标

2.2.1.1 原实际取水量

这是一个参考性指标，体现了微观主体农用水权初始分配的水源地优先原则和用水现状优先原则。一方面，同一地区不同区域的产水量可能是不同的，这是不同区域水资源禀赋的自然原因造成的。这一差异是不同区域发展农业的重要自然资源，在进行农用水权初始分配是要充分考虑这一因素[5]； 另一方面，由于水资源天然禀赋以及节水设施投入等方面的不同，为了尊重和维持各微观主体用水现状，避免一些不必要的纠纷，保证农用水权初始分配顺利进行，考虑原实际取水量也是有必要的。该文在构建模型时要求各微观主体的水权分配量与该指标保持正相关关系。

2.2.1.2 农地面积

农地面积体现了土地流转之后，微观主体承包的需灌溉的农业用地的面积。该指标值越大，需水量越大，也应该分配相对较多的初始水权。

2.2.1.3 农地实际灌溉面积

农地实际灌溉面积指的是在农地面积中已经实际进行正常灌溉的农地面积。因此，农地实际灌溉面积不大于农地面积。

2.2.2 效率性指标

水资源是缺水地区农业生产和社会经济发展的关键自然资源，在进行微观主体农用水权初始分配时，不仅要考虑公平性指标，更要考虑效率性指标，也就是给予用水效率高的区域和微观主体相对较多的初始水权，反之亦然。

2.2.2.1 农地实灌单位面积用水量

农地实灌单位面积用水量直接反映了农业灌溉用水效率，并在一定程度上反映了微观主体对水资源的需求强度。

2.2.2.2 单位土地面积农业产值

单位土地面积农业产值指标暂时以GDP来衡量，体现了微观主体在单位土地面积上进行农业生产的效率，这一指标值的大小是包括水资源在内的多种因素共同作用的结果。该指标值越大，应当分配较多的初始水权，以在一定程度上促使微观主体利用多种手段提高农业生产效率，从而提高水资源利用效率。

2.2.2.3 单位水农业产值

单位水农业产值体现了微观主体单位用水量所带来的产值的大小，暂时以GDP衡量。这也是一个反映水资源利用效率的重要指标。如果该指标值较小，表明水资源利用效率较低，应当分配较少的初始水权； 反之，表明水资源利用效率较高，应当分配较多的初始水权，以此作为一种激励手段，引导农业灌溉用水向效率高的区域和微观主体流动[5]。

2.2.2.4 节水设施投入

节水设施投入体现了微观主体在节约农业灌溉用水方面资金投入量的多少。该指标值越大，反映微观主体节水意识越强，节水投入资金也越多，分配的初始水权也应当较多，反之亦然。该指标可以有效引导微观主体投入更多的财力、物力用于节约农业灌溉用水。

2.3 模型构建

2.3.1 投影寻踪指标函数的建立

2.3.1.1 建立农用水权初始分配样本集，并将其进行数据归一化处理

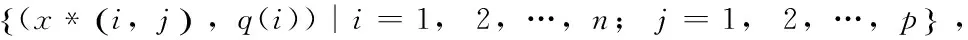
如果是越大越优型指标，则公式为

x(i，j)=[x*(i，j)-xmin(j)]/[xmax(j)-xmin(j)]

(1)

如果是越小越优型指标，则公式为

x(i，j)=[xmax(j)-x*(i，j)]/[xmax(j)-xmin(j)]

(2)

式(2)中，xmax(j)、xmin(j)分别为样本集中第j个指标值的最大值和最小值。

2.3.1.2 构造投影指标函数

使用投影寻踪方法可以把p维数据{x*(i，j)|j=1， 2，…，p}综合成以a=(a(1)，a(2)，…，a(p))为投影方向的一维投影值z(i)。

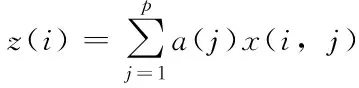
(3)

然后，根据{z(i)|i=1， 2，…，n}的一维散布图进行分类，式中a为单位长度向量。在综合投影值时，要求投影值z(i)的散布特征应为：局部投影点尽可能密集，最好凝聚成若干个点团； 而在整体上投影点团之间尽可能散开； 同时，为了保持进行水权分配后的各微观主体的取水量与水权分配之前的实际取水量保持相对一致，则要求z(i)与q(i)的相关系数R的绝对值以及z(i)的标准差S均尽可能大。据此投影指标函数可构造为

Q(a)=Sz|R|

(4)

式(4)中，Sz为投影值z(i)的标准差，R为z(i)与q(i)的相关系数，即

(5)

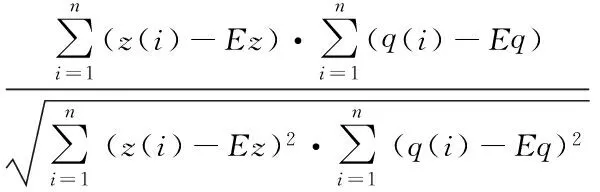
(6)

式(6)中，Ez，Eq分别为序列{z(i)}和{q(i)}的均值

2.3.1.3 优化投影指标函数

当各指标值的样本集给定时，投影指标函数Q(a)只随投影方向a的变化而变化。可通过求解投影指标函数最大化问题来估计最大可能暴露高维数据某类特征结构的最佳投影方向，因此，投影指标函数可以优化为：

目标函数：maxQ(a)=Sz|R|

(7)

(8)

以{a(j)|j=1， 2，…，p}为优化变量的复杂非线性优化问题，目标函数采用混沌粒子群优化算法求解。

2.3.1.4 基于CPSO的投影方向优化

粒子群优化算法具有通用性强、所需调节参数较少、随机初始化等特点，但容易陷入局部最优解。而混沌优化算法可在一定范围内不重复遍历所有状态，避免陷入局部极小点，可是混沌优化算法需要较多的迭代次数，否则不易获得较优的解[4]。因此，该文将二者结合起来构造混沌粒子群优化算法(CPSO)，利用混沌的遍历特征，产生大量的初始样本，从中选取优良的样本个体用于迭代，迭代过程中对粒子位置产生混沌扰动，避免其陷入局部极值[4]。

根据混沌优化算法，上述有约束条件的目标函数要转化为无约束条件的函数求解问题[7]，该文采用Hestenes乘子法将其转化为无约束条件的函数求解问题，即

(9)

对于此函数可以采用迭代公式uk+1=uk+σkh(ak)，在给定的算法终止运算准则||h(ak)||<ε下求解，其中，ε为误差精度，且ε>0。对于每一次迭代都可以使用CPSO算法求解，具体流程如图2所示。

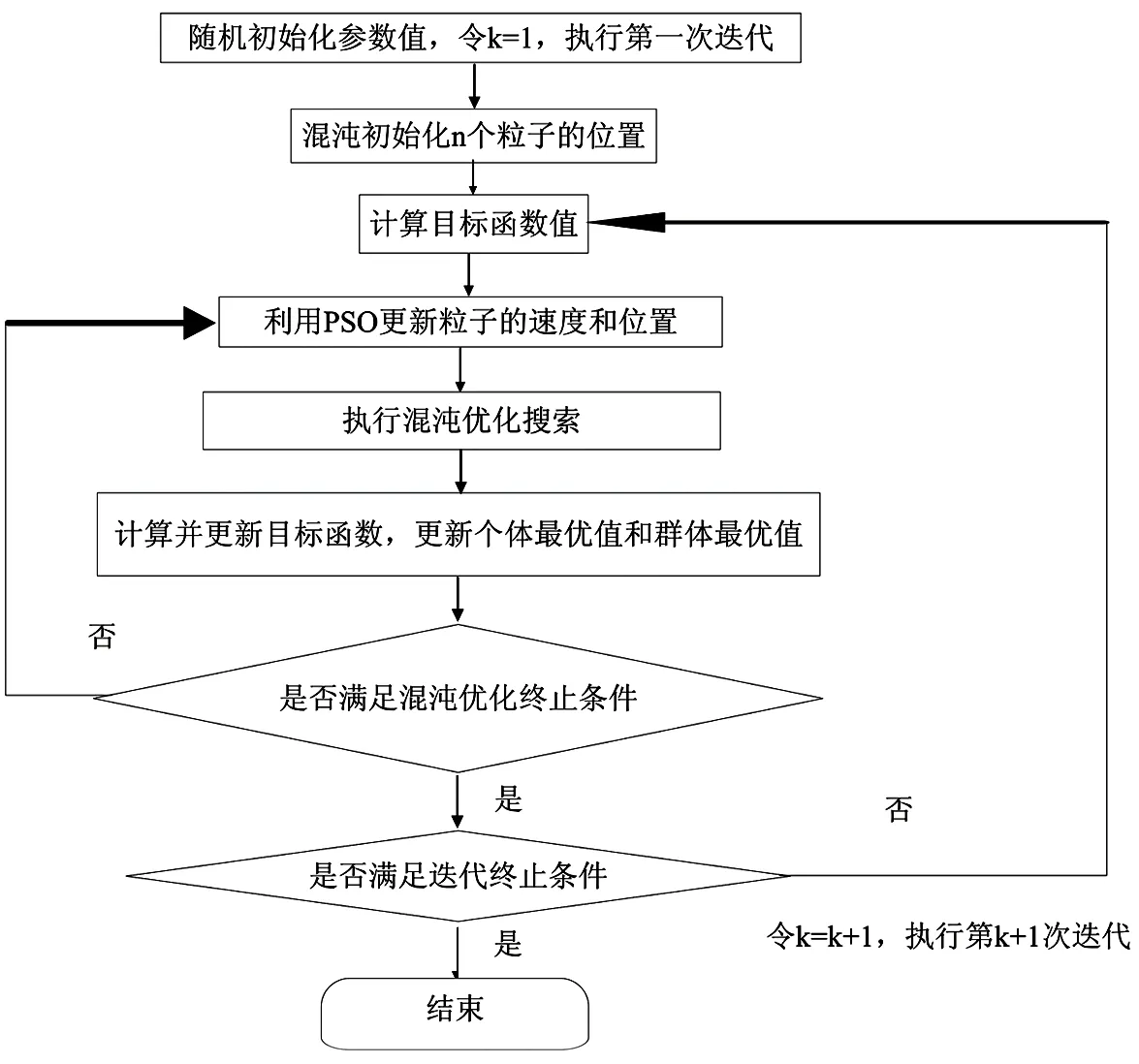
图2 基于CPSO的投影寻踪目标函数求解流程

3 算例验证及分析

已知A地区实施土地流转后，达到了比较好的土地规模化效果，大部分农业用地非常集中，包括林果地、草地等。其中灌溉用地主要涉及8个微观主体，相关数据如表1所示。

将表1中各指标值进行归一化处理后得到数据如表2所示，根据表2数据建立投影指标函数，采用混沌粒子群优化算法求解，分别经过10至130次迭代后，目标函数值φ基本稳定于0.7885，如图3所示，最佳投影方向a*=(0.6577， 0.5605， 0.2601， 0.1201， 0.2013， 0.3508)。从图3中可以看出，混沌粒子群优化算法较混沌优化算法收敛速度较快，适用于投影方向的确定[4]。将最佳投影方向a*代入式(3)后即可得到水权分配的投影值Z(i)*=(1.2766， 0.6139， 1.6916， 0.8749， 0.7165， 1.5582， 0.3413， 0.7891)，将其进行归一化处理后即可得到各微观主体分水比例，然后将农业灌溉的用水总量WR与各分水比例相乘，便可得到各微观主体初始水权分配量，如表3所示。

表1 农用水权分配样本值

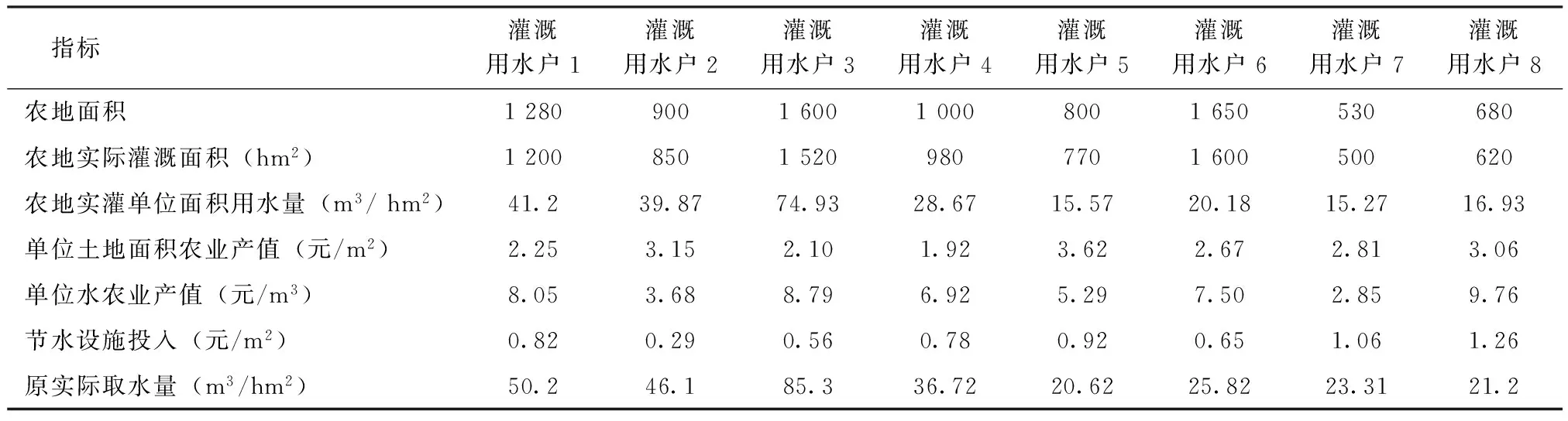
指标灌溉用水户1灌溉用水户2灌溉用水户3灌溉用水户4灌溉用水户5灌溉用水户6灌溉用水户7灌溉用水户8农地面积1280900160010008001650530680农地实际灌溉面积(hm2)120085015209807701600500620农地实灌单位面积用水量(m3/hm2)41.239.8774.9328.6715.5720.1815.2716.93单位土地面积农业产值(元/m2)2.253.152.101.923.622.672.813.06单位水农业产值(元/m3)8.053.688.796.925.297.502.859.76节水设施投入(元/m2)0.820.290.560.780.920.651.061.26原实际取水量(m3/hm2)50.246.185.336.7220.6225.8223.3121.2

表2 各指标归一化处理结果

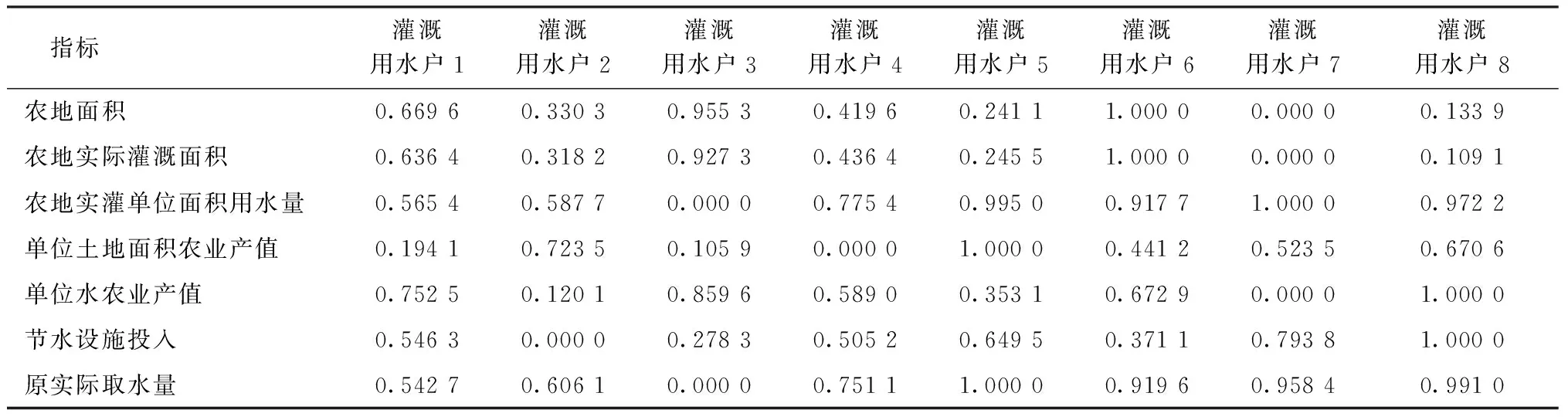
指标灌溉用水户1灌溉用水户2灌溉用水户3灌溉用水户4灌溉用水户5灌溉用水户6灌溉用水户7灌溉用水户8农地面积0.66960.33030.95530.41960.24111.00000.00000.1339农地实际灌溉面积0.63640.31820.92730.43640.24551.00000.00000.1091农地实灌单位面积用水量0.56540.58770.00000.77540.99500.91771.00000.9722单位土地面积农业产值0.19410.72350.10590.00001.00000.44120.52350.6706单位水农业产值0.75250.12010.85960.58900.35310.67290.00001.0000节水设施投入0.54630.00000.27830.50520.64950.37110.79381.0000原实际取水量0.54270.60610.00000.75111.00000.91960.95840.9910

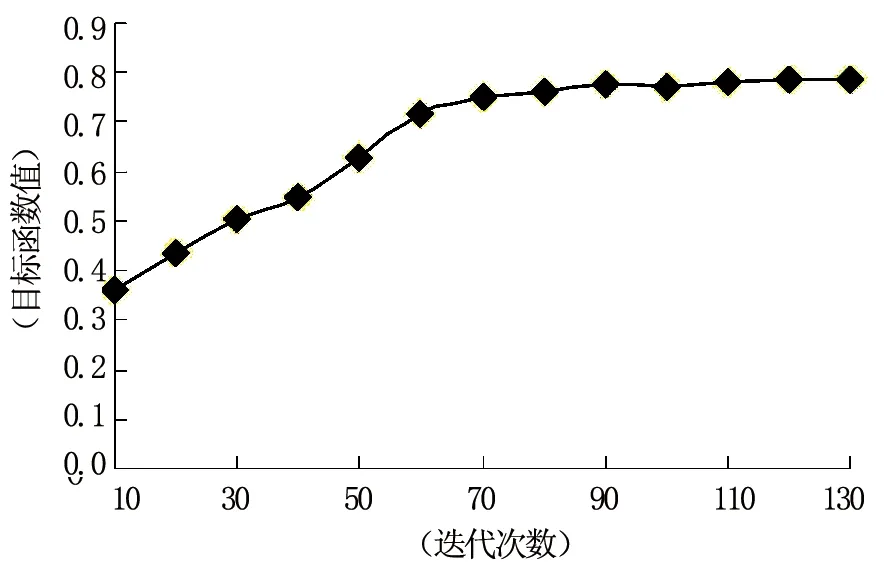
图3 目标函数值与迭代次数变化曲线

灌溉用水户投影值分水比例(%)微观主体11.276616.24微观主体20.61397.81微观主体31.691621.52微观主体40.874911.13微观主体50.71659.11微观主体61.558219.82微观主体70.34134.33微观主体80.789110.03

与层次分析法相比，投影寻踪技术直接由样本驱动，通过最佳投影方向确定决策方案最优值，避免了层次分析法构造判断矩阵时需要人为主观赋予权重的缺陷[3]，而混沌粒子群优化算法与混沌优化算法相比具有收敛速度快、迭代次数少的优势。同时，该文计算的结果也符合初始水权分配的公平性和效率性原则，说明了模型的合理性。

4 结论

该文在前人研究基础上提出了将粒子群优化算法和混沌优化算法结合起来的思路，利用投影寻踪的技术来研究初始水权分配问题，避免了采用层次分析法研究这一问题时在权重确定上受主观因素影响较大的不利因素，同时解决了单纯的混沌优化算法在全局寻优时迭代次数过多、速度过慢的问题，并通过算例分析，验证了该模型的可行性和合理性，丰富和发展了初始水权分配的思路和方法。另外，该文构建的模型具有较强的适应性、灵活性和可扩展性，可根据实际情况的不同，选取不同的水权分配指标体系，对该模型进行完善和补充。

[1] 钱焕欢，倪焱平.农业用水水权现状与制度创新.中国农村水利水电， 2007，(5)： 138～141

[2] 郑志来. 土地流转背景下缺水地区农业水权置换制度影响因素研究.农村经济, 2015，(3)： 90～94

[3] 杨芳， 肖淳，邵东国，等.基于投影寻踪混沌优化算法的流域初始水权分配模型.武汉大学学报(工学版)， 2014, 47(5): 621～624

[4] 马智泉， 李鹏，王魁.混沌粒子群优化投影寻踪法在电能质量监测网中的应用.水电能源科学， 2012, 30(5): 181～185

[5] 尹云松， 孟令杰.基于AHP的流域初始水权分配方法及其应用实例.自然资源学报， 2006, 21(4): 645～651

[6] 付强， 赵小勇.投影寻踪模型原理及其应用.北京：科学出版社， 2006

[7] 王魁， 张步涵，胡永强.考虑储能装置风电场的动态经济调度.湖北工业大学学报， 2011, 26(1): 1～5

[8] 李新， 常福宣，陈进.水权与初始水权分配研究综述.长江科学院学报， 2011, 28(2): 1～9

[9] 孙建光， 韩桂兰.塔里木河流域绿洲可转让农用水权及其分配问题研究.节水灌溉, 2013，(11)： 66～72

[10]张戈跃. 试论我国农业水权转让制度的构建.中国农业资源与区划， 2015, 36(3): 98～102

[11]户艳领， 陈志国，刘振国.基于熵值法的河北省农业用水利用效率研究.中国农业资源与区划， 2015, 36(3): 136～142

[12]王俊杰， 王娟娥，方金.构建资源节约型农业综合评价指标体系研究——以山东省为例.中国农业资源与区划，2014， 35(4)： 41～48

ANALYSIS OF INITIAL AGRICULTURAL WATER RIGHT ALLOCATION IN WATER SHORTAGE AREA IN THE BACKGROUND OF LAND CIRCULATION*——BASED ON THE MODEL OF PROJECTION PURSUIT AND CHAOTIC PARTICLE SWARM OPTIMIZATION

Zhang Xue，Zheng Zhilai※

(School of Business ,Yancheng Normal College, Yancheng, Jiangsu 224051, China)

The paper constructed an evaluation index system of initial agricultural water right allocation in water shortage area by selecting six indicators related to fairness and efficiency, and then established the Chaotic particle swarm optimization (CPSO) and projection pursuit (PP) model to research the initial agricultural water right allocation in water shortage area in the background of land circulation. The PP model was adopted to reduce the dimensions of the decision-making problem of initial agricultural water right allocation and the CPSO model was used to search the optimum projection direction. Meanwhile, the feasibility, reasonableness and effectiveness of the model were verified by an example calculation and comparative analysis. The empirical analysis results showed that land circulation made agricultural production towards land scale, professionalism of the main body, agricultural specialization, and gradual centralization of agriculture; What′s more, the clarity of agricultural water right could optimize agricultural water structure, agricultural water conservation, agricultural water rights exchange, and promote agricultural water rights transform from agriculture to secondary industry and tertiary industry. It also could improve the optimization and upgrading of industrial structure, social development and economic transformation. The optimum value of various schemes should be calculated objectively and the weight of each index should be determined fairly, based on the sample data of various areas. Additionally, a complete initial agricultural water right allocation system should take into account the factors, such as laws, systems, policies, socio-economic, ecological and environmental factors.

micro-units; agricultural water right allocation; pursuit projection; CPSO

10.7621/cjarrp.1005-9121.20170224

2016-03-25 作者简介：张雪(1984—)，男，江苏徐州人，硕士、讲师。研究方向：区域经济。※通讯作者：郑志来(1981—)，男，江苏盐城人，博士、副教授。研究方向：资源管理。Email：haokgo@126.com *资助项目：国家社会科学基金项目“土地流转、农用水权置换与缺水地区产业结构优化研究”(14CJY029)

TV213; F322

A

1005-9121[2017]02168-07