含有Siegel盘的多项式的扰动

徐 玲, 杨文钰, 周 吉*

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 石河子大学 数学系, 新疆 石河子 832000)

含有Siegel盘的多项式的扰动

徐 玲1, 杨文钰2, 周 吉1*

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 石河子大学 数学系, 新疆 石河子 832000)

讨论具有Siegel盘且次数m>2的多项式P(z),构造函数列

拟共形映射; Siegel盘; Hartogs延拓定理

1 预备知识

解析函数的Siegel盘的存在性是解析函数局部动力学的一个重要内容[1-4].设原点为解析函数的不动点,且在原点附近可表示为

f(z)=e2πiαz+O(z2),

(1)

这里α为无理数.已经知道:Siegel盘的存在性与α的性质有很大的关系[3,5].设pn/qn是实数α的第k个渐进分数,即是最佳有理逼近.如果

称α为Brjuno数,用B表示这些Brjuno数所组成的集合.G. A. Bogar[6]得到：当α∈B,由(1)式所定义的函数f(z)在0点存在一个Siegel盘.J. C. Yoccoz[7]还得到：二次多项式在原点存在Siegel盘的充要条件是α∈B.因此,对于d次多项式

P(z)=e2πiαz+c2z2+c3z3+…+cdzd,

当α∈B,如果对次数大于1的项进行扰动,所得到的多项式仍然在原点存在一个Siegel盘.最近,文献[8]得到如下结果.

引理 1.1[8]设f和fn是定义在原点的某个邻域U上的解析函数,其中

fn(z)=e2πiαnz+O(z2).

若对任意n,fn在原点都有Siegel盘,并且fn在U的任意紧子集上收敛于f,则f在原点也存在Siegel盘.

反过来,如果一个解析函数在原点有Siegel盘,是否存在收敛于该函数的解析函数列,它的每个元素在原点处都有Siegel盘?就多项式的情形,本文对该问题给出了正面的回答.

为了得到本文的结果,需要拟共形映射和多复变函数方面的一些基本知识.

则称f是拟正则的.

引理 1.3[10]对于区域Ω上的复值函数μ,‖μ‖∞表示μ在Ω上的本性上界,若μ是Lebesgue可测的且满足‖μ‖∞<1,则称μ为Ω上的一个Beltrami系数.

引理 1.4[10]假设f:U→V是拟正则的,μ:V→C为Beltrami系数,定义μ在f下的拉回

利用Hartogs延拓定理[12-13]可以得到下列结果.

引理 1.6 多复变解析函数无孤立零点.

2 主要结果及证明

定理 2.1 假设次数(m>2)的多项式

P(z)=λz(1+a2z2+…+amzm-1),

λ=e2πiα,α是无理数,在原点有Siegel盘S,那么存在函数列

Qn(z)=P(z)+Am-1(n)zm-1+…+A2(n)z2,

其中,Ai(n)(i=2,3,…,m-1)不全为0,(Qn)收敛于P,并且对每个n,Qn与P在原点都有Siegel盘,且包含原点的某邻域S0.

注 2.1 当m=2时,J. C. Yoccoz[7]的结果表明上述结论仍成立.

证明 当P仅有一个非零零点时,借助于共形共轭,不妨设复平面上的m次多项式P形如P(z)=λz(cz-1)m,λ=e2πiα,α为无理数,c是复平面上非零常数,并且在原点有Siegel盘S.由文献[14]知,存在

Qa(z)=P(z)+c(a)z2g(z),

对任意a满足|a|<δ,都存在Siegel盘,并且包含原点的某邻域S0,其中,f、g、c解析,c(0)=0,g(0)≠0.特别地,将a取为序列(1/n)有

因此,(Qn)收敛于P,并且对每个n,(Qn)与P在原点的Siegel盘包含原点的某邻域S0.

当P有2个不同非零零点时,设复平面上的m次多项式P形如

P(z)=λz(z-z1)(z-z2)g(z),

λ=e2πiα,α为无理数,非零零点z1≠z2,g(0)≠0,在原点有Siegel盘S,则有

P-1(S)⊃S∪S1∪S2,

其中,S1和S2分别是包含z1和z2的Fatou分支.选择适当的ε>0使得D2ε(zi):={z∈C||z-zi|<2ε}⊂Si,i=1,2.选择ξ(t)∈C∞,ξ(t):[0,+∞)→[0,1],其中,当t≤1时,ξ(t)=1;当t≥4时,ξ(t)=0.对a,b∈C,定义

Pa,b(z)=P(z)+

显然,Pa,b∈C∞.令Λi={z∈C|ε≤|z-zi|≤2ε},i=1,2,则有

下面证明在a和b适当的取值范围内,Pa,b关于z是拟正则函数.当z∈C(Λ1∪Λ2)时,有Pa,b(z)=P(z)或Pa,b(z)=P(z)+a或Pa,b(z)=P(z)+b.因此,Pa,b解析并且Pa,b在C(Λ1∪Λ2)上是拟正则的.当z∈Λ1∪Λ2时,Pa,b∈C∞.下面只需要计算在(Λ1∪Λ2)上的复特征

因为ξ(t)∈C∞并且ξ′(t)有紧支撑,故

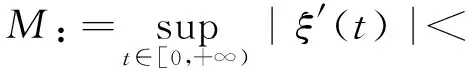
选择合适的ε使得

因此

故μPa,b(z)关于a和b是解析映射.令δ=mε/(12M).若|a|<δ,|b|<δ有

所以,对z∈(Λ1∪Λ2),|a|≤δ以及|b|≤δ,有‖μPa,b‖≤1/2,其中,‖·‖是本性上界,Pa,b是3-拟正则的.因此μPa,b是Beltrami系数.

接下来在复平面C上构造不变的Belrtami系数μa,b.首先对Beltrami系数作拉回,并且拉回后仍然是Betrami系数.

由于Pa,b的轨道只要进入(Λ1∪Λ2),最终将留在S中.因此定义

μa,b(z):=

则有

其中,Pn表示P的n次迭代,IP-n(Λ1∪Λ2)表示P-n(Λ1∪Λ2)的特征函数.由最后的和式可知μa,b(z)是可测的.此外,μa,b(z)关于a和b解析.由于区域(Λ1∪Λ2)关于P和Pa,b的原像在C(D2ε(z1)∪D2ε(z2))上且相等,则有

或者

则有

μa,b是Pa,b在C上不变得Beltrami系数.由引理1.5知,存在拟共形映射φa,b:C→C,μφa,b=μa,b满足φa,b(0)=0,φa,b(∞)=∞,φa,b(z1)=z1.令

Qa,b(z)-P(z)=Am(a,b)zm+

Am-1(a,b)zm-1+…A2(a,b)z2,

其中,Ai(i=2,3,…,m)和z无关并且关于a和b在|a|<δ和b|<δ上解析.

由于(a,b)=(0,0),记Q0,0:=Q,φ0,0:=φ有

Q(z)=φ∘P∘φ-1(z).

由于P在C上解析,则复特征μP=0,φ在C上是共形映射,即Möbius变换.由于φ(∞)=∞,φ(0)=0,φ(z1)=z1,φ是恒等映射,即Q=P.因此

Ai(0,0)=0,i=2,3,…,m.

由引理1.6,存在极限为(0,0)的收敛点列cn:=(an,bn),对任意n,0<|an|<δ,0<|bn|<δ,使得

Am(an,bn)=0,n=1,2,….

记(a0,b0)=(0,0),Ai(n):=Ai(an,bn),Qn:=Q(an,bn),则有

Qn(z)=P(z)+Am-1(n)zm-1+…+A2(n)z2.

由Ai解析且Ai(0,0)=0,i=2,3,…,m有

Am-1(n)zm-1+…+A2(n)z2)=P(z).

下面证明对任意正整数n,Qn≠P.事实上,只需证明存在整数k,2≤k≤m-1,Ak(n)≠0.

由于φn是拟共形的,因此在0<|an|<δ时,φn(an)≠0.又由

Qn(z1)=P(z1)+Am-1(n)zm-1+…+A2(n)z2,

=Am-1(n)zm-1+…A2(n)z2.

因此

Am-1(n)zm-1+…+A2(n)z2=φn(an)≠0,

即存在整数k,使得2≤k≤n-1,Ak(n)≠0.

最后,证明对每个n,Qn与P在原点的Siegel盘包含原点的某邻域S0.

在P的Siegel盘S上,Pa,b≡P且φa,b是共形的,故Pa,b有Siegel盘S,又

则对任意|a|<δ,|b|<δ,Qa,b有Siegel盘φa,b(S),且φa,b(0)=0,φa,b(∞)=∞,φa,b(z1)=z1,由文献[15],函数族φa,b是3-拟共形的正规族,故φa,b是等度连续的.由此可知Qa,b与P在原点的Siegel盘φa,b(S)(|a|<δ,|b|<δ)包含原点某固定邻域S0.

特别地,对于收敛于(0,0)的点列(an,bn),|an|<δ,|bn|<δ,(Qn)与P在原点的Siegel盘都包含邻域S0.证毕.

[1] CARLESON L, GAMELIN T. Complex Dynamics[M]. New York:Springer-Verlag,1993.

[2] 吕以辇. 复解析动力系统[M]. 北京:科学出版社,1995.

[3] MILNOR J. Dynamics in One Complex Variable[M]. Princeton:Princeton University Press,2006.

[4] 任福尧,邱维元. 复解析动力系统[M]. 上海:复旦大学出版社,1997.

[5] SIEGEL C L. Iteration of analytic functions[J]. Ann Math,1942,43(4):607-612.

[6] BOGAR G A. Oscillation properties of two term linear differential equations[J]. Transactions of the American Mathematical Society,1971,161:25.DOI:10.2307/1995925.

[7] YOCCOZ J C. Theorem de Siegel, nombres de Brjuno et polynomials ratiques[J]. Asterisque,1995,231:3-88.

[8] BUFF X, CHÉRITAT A. A new proof of a conjecture of Yocooz[J]. Ann Inst Fourier, Grenoble,2011,61:319-350.

[9] BRANNER B, FAGELLA N. Quasicconformal Surgery in Holomorphic Dynamics[M]. Cambrige:Cambrige University Press,2014.

[10] 崔贵珍. 复分析[M]. 北京:科学出版社,2014.

[11] 李忠. 复分析导引[M]. 北京:北京大学出版社,2004.

[12] FRITZSCHE K, GRAUERT H. From Holomorphic Functions to Complex Manifolds[M]. New York:Springer-Verlag,2002.

[13] STEVEN G K. The Hartogs extension phenomenon redux[J]. Complex Variables and Elliptic Equations,2011,53(4):343-353.

[14] GEYER L. Siegel discs, Herman rings and the Arnold family[J]. Transactions of the American Mathematical Society,2001,353(9):3661-3683.

[15] LEHTO O, VIRTANEN K I. Quasiconformal mappings in the plane[J]. Die Grundlehren Der Mathematischen Wissenschaften,1973,90(24):11958-11959.

2010 MSC：37F50

(编辑 李德华)

Perturbation of a Polynomial with a Siegel Disk

XU Ling1, YANG Wenyu2, ZHOU Ji1

( 1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan; 2.DepartmentofMathematics,ShiheziUniversity,Shihezi832000,Xinjiang)

In this paper, we show that for any polynomialP(z) of degreem>2 with a Siegel disk centered at 0, there exists a sequence of functions of formQn(z)=P(z)+Am-1(n)zm-1+…+A2(n)z2,whereallAi(n)(i=2,3,…,m-1) are not all equal to 0, such thatQnconverges toP. Moreover, eachQnhas a Siegel disk containing a fixed neighborhood of 0.

quasiconformal mapping; Siegel disk; Hartogs extension

2016-01-05

国家自然科学基金(11371266)、教育部博士点专项基金(20095134110001)和四川省应用基础研究项目(07JY029-013)

O174.5

A

1001-8395(2017)03-0285-04

10.3969/j.issn.1001-8395.2017.03.001

*通信作者简介：周 吉(1963—),男,教授,主要从事复分析的研究,E-mail:zhouji@sicnu.edu.cn

Qn=P(z)+Am(n)zm+Am-1(n)zm-1+…+A2(n)z2,

其中Ai(n)(i=2,3,…,m-1)不全为0,使得Qn收敛于P.而且,对每个n,Qn在原点的Siegel盘都包含原点的某固定邻域.