采用图像处理的织物缝纫平整度自动评估

张 宁， 潘如如， 高卫东

(生态纺织教育部重点实验室(江南大学)， 无锡 江苏 214122)

采用图像处理的织物缝纫平整度自动评估

张 宁， 潘如如， 高卫东

(生态纺织教育部重点实验室(江南大学)， 无锡 江苏 214122)

为解决织物缝纫平整度客观自动评估时分类正确率低的问题，提出了一种基于灰度共生矩阵、小波分析和反向传播(BP)神经网络相结合的织物缝纫平整度的自动评估方法。首先采集标准缝纫图像，将图像的灰度级降至16级，计算图像在0°和90°方向上的灰度共生矩阵并将其归一化，提取灰度共生矩阵的能量、熵、对比度和相关性4个特征参数，并分别对特征参数在0°和90°方向上取均值；同时，运用Haar小波在第6个分析尺度上提取并计算图像的水平细节系数的标准差。然后将提取的这5个特征参数输入到BP神经网络中训练和识别，并对标准缝纫图像进行了评估。评估结果显示：提出的算法与单独采用灰度共生矩阵特征、小波特征相比，具有较高的分类正确率，分类效果稳定。

缝纫平整度； 灰度共生矩阵； 小波分析； BP神经网络

在服装加工缝合或洗涤过程中，由于面料的力学性能、缝纫机器参数、操作不当和洗涤条件等因素的影响，在接缝线的两侧产生一定程度的褶皱，称为缝纫平整度。缝纫平整度是质量控制的重要指标，直接影响到服装的外观效果。目前对于织物缝纫平整度的评估，主要是通过人工将缝纫试样与ISO 7770：2009《纺织品洗涤后织物接缝外观平整度的评定方法》或AATCC 88B—2006《织物经多次家庭洗涤后缝线平整度测定》标准的图像相对照，为试样评定相应的等级。这种方法不仅耗时费力，而且易受主观因素的影响。通过计算机技术来主观、快速、准确地实现对织物缝纫平整度的自动评估，可避免人为因素的影响，提高分类正确率。

目前，在织物缝纫平整度的客观评估研究中，主要是通过特征提取和分类识别2部分来完成。首先提取图像的特征向量作为分类的依据，然后利用分类方法或分类器实现对缝纫平整度的自动评估。特征提取的方法主要有图像的灰度投影、傅里叶分析[1]、表面粗糙度[2]、分形理论[3]、小波分析[4]和灰度共生矩阵[5]等，分类方法或分类器主要有模糊C均值聚类(FCM)分析、模糊模式识别[6]、回归分析[1]、人工神经网络[5,7]和支持向量机等。缝纫试样图像采集系统主要分为二维和三维2种方式，在二维的采集系统中，主要采用照相机或扫描仪来采集图像；对于三维的采集系统，Fan等[8]利用激光扫描仪和切比雪夫波段过滤器来提取织物表面平行于接缝线的轮廓。Koehl等[9]提出了一种三维数字化系统来生成三维缝合试样模型。Kang等[10]使用了一种三维的、非接触的扫描系统。在现有的这些研究中，很多的特征提取方法只是提取全局或局部的特征，不能全面地反映不同缝纫等级之间的差异，分类正确率的大致范围在80%～90%之间不等，分类正确率有待于提高。

本文提出了一种基于灰度共生矩阵、小波分析和反向传播(BP)神经网络相结合的织物缝纫平整度的自动评估方法。通过采集标准缝纫试样图像，运用灰度共生矩阵提取能量、熵、对比度和相关性4个特征参数，代表缝纫图像的全局信息，同时运用小波分析提取水平细节系数，代表缝纫图像的局部细节信息，将二者的特征参数相结合作为特征向量输入到BP神经网络中集成，实现对织物缝纫平整度的自动评估，具有较高的分类正确率。

1 缝纫图像的采集与预处理

1.1 图像采集

图1示出图像的采集系统。由相机(Canon Rebel EOS 1000D)、试样平台(RPS Studio, RS-CS1070)、支架和光源(Canon, Speedlite 270EX II)4部分组成。相机通过一个USB3接口与电脑相连，设置在AE程式拍摄模式，拍摄速度和光圈可通过编程的方式设置。在试样的一侧采用倾斜的光照方式，可增强起皱部分的亮度变化。

图1 图像采集系统Fig.1 Image acquisition system

为得到稳定的分类结果，为后续的研究寻找稳定的方法，实验中采用ISO 7770:2009《纺织品洗涤后织物接缝外观平整度的评定方法》的缝纫试样作为采集图像的实验样本，用于分类识别部分的训练集和预测集。采用的相机分辨率为3 888像素×2 592像素，对应的物理尺寸为152 mm×102 mm的可视区域，即0.039 mm/像素的分辨率。图2示出采集的一幅经预裁剪后的标准缝纫图像。

图2 经预裁剪后的标准缝纫图像Fig.2 Normative seam image after pre-cropping

1.2 图像预处理

对于采集到的缝纫试样图像，首先采用Canny边缘检测算法检测接缝线的位置；然后采用Hough变换检测接缝线倾斜的角度，并将其旋转相应角度，使得接缝线处于水平位置；接着以接缝线为中心，在接缝线两侧裁剪图像，裁剪后的图像为2 000 像素×200像素；最后为消除倾斜光照导致的图像亮度不均，对图像进行亮度均衡化，得到亮度均匀的图像。图像的预处理流程如图3所示。

图3 图像预处理流程Fig.3 Pre-processing flow of seam image. (a) Position of seam-line; (b) Adjusted seam image after rectifying; (c) Seam image after cropping; (d) Seam image after intensity adjustment

2 缝纫图像特征参数的提取

2.1 灰度共生矩阵

2.1.1 灰度共生矩阵及其参数

灰度共生矩阵是通过计算图像中一定距离和一定方向上的2点灰度之间的相关性来描述纹理的常用方法，反映了图像在方向、相邻间隔、变化幅度及快慢上的综合信息。设f(x,y)为一幅大小为M×N的二维数字图像，灰度级别为G，则满足一定空间关系的灰度共生矩阵为

P(i,j)=#{(x1,y1),(x2,y2)∈

M×N|f(x1,y1)=i,f(x2,y2)=j}

(1)

其中，#{x}表示集合{x}中的元素个数[11]，P为G×G的矩阵。

假设在θ方向上，2个像素之间的距离为d，则其灰度共生矩阵可表示为P(I,j,d,θ)。θ的取值为0°、45°、90°、135°，d的取值一般与图像有关，可根据实验来确定。在本文实验中，角度θ选择0°和90°，距离d选择4[5]。由于该实验中的缝纫试样图像的灰度级为256，灰度级过大将导致运算量增加，影响处理速度，所以在计算灰度共生矩阵之前需要对图像进行降级处理。本文选用等级为16[12-13]的灰度级，以减少运算量，提高程序的处理速度。

在相应的参数确定之后，分别计算2个像素之间的距离为4时，图像在0°和90°方向上的灰度共生矩阵，并对矩阵进行归一化处理。

2.1.2 特征参数的提取

根据计算得到图像的灰度共生矩阵，可从中提取特征值来分析图像的局部模式和排列规则等信息。Haralick等提取了14种特征值[11]，但是Ulaby等[14]研究发现这些特征之间存在着冗余，一般选用能量、熵、对比度和相关性这4个特征值作为图像分类的依据，定义如下。

1)能量：

(2)

2)熵：

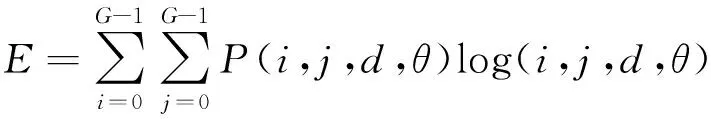
(3)

3)对比度：

(4)

4)相关性：

(5)

其中：

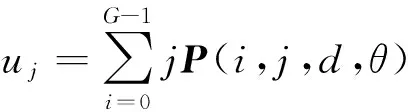
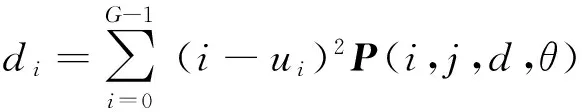
对于每幅图像，在提取特征参数时，首先计算0°和90°方向上灰度共生矩阵的4个特征参数，然后分别对不同的特征值在2个方向上取均值，可得到4个特征参数。采用这样的处理方式，可抑制方向分量对纹理特征的影响。

2.2 小波分析

2.2.1 小波分析理论

小波分析技术是一种在不同尺度上分析图像纹理细节的方法，可通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析。小波分析在时域和频域都能表征信号的局部信息，能有效地从信号中提取信息。

以一维信号为例，小波变换是以小波函数Ψa,τ(t)为基底对信号f(t)进行分解，小波函数是由同一基底函数Ψ(t)经平移、伸缩得到的一组函数，如式(6)、(7)所示：

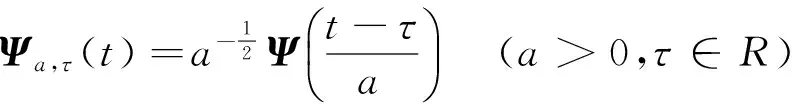
(6)

(7)

式中：a为伸缩因子；τ为平移因子。

利用小波变换，可将信号通过低通和高通滤波器分解为近似系数和细节系数，逐步进行多尺度细化，最终达到高频处时间细分、低频处频率细分，可聚焦到信号的任意细节。

2.2.2 二维离散小波变换

缝纫图像可被看作是一个由低频信号(图像的主体)、高频信号(噪声和边缘)及中高频信号(缝纫不平整造成的褶皱)迭加的复杂信号，小波分析的时频局域化特别适合提取这类信号的特征信息[15]。对于这样的二维信号，通常采用二维离散小波变换进行处理。二维离散小波变换是对二维图像信号在水平和垂直方向作相同的一维离散小波变换，得到4组系数[Aj,Hj,Vj,Dj]。其中，Aj为第j层的近似系数，Hj、Vj、Dj分别为第j层的水平、垂直和对角细节系数。

通过选用合适的小波和分析尺度，可提取反映图像纹理细节的系数。常用的小波有Haar小波、Coiflet order 1小波、Symlets order 4小波等[4]，小波的种类和分析尺度可根据文献[4]中提出的评估因子来确定，使得特征值呈现线性变化和评估因子的值最大。通过实验分析，当选用Haar小波、分析尺度为6时，特征值随平整度等级的增加而增加，且评估因子的值最大。采用Haar小波、在分析尺度为6时分解图像，并重构水平细节系数，计算水平细节系数的标准差作为图像的特征参数。

3 缝纫图像特征参数的训练

3.1 BP神经网络

BP神经网络是一种按误差反向传播算法训练的多层前馈网络， 由输入层、隐层和输出层3部分组成。图4示出BP神经网络的模型结构图。

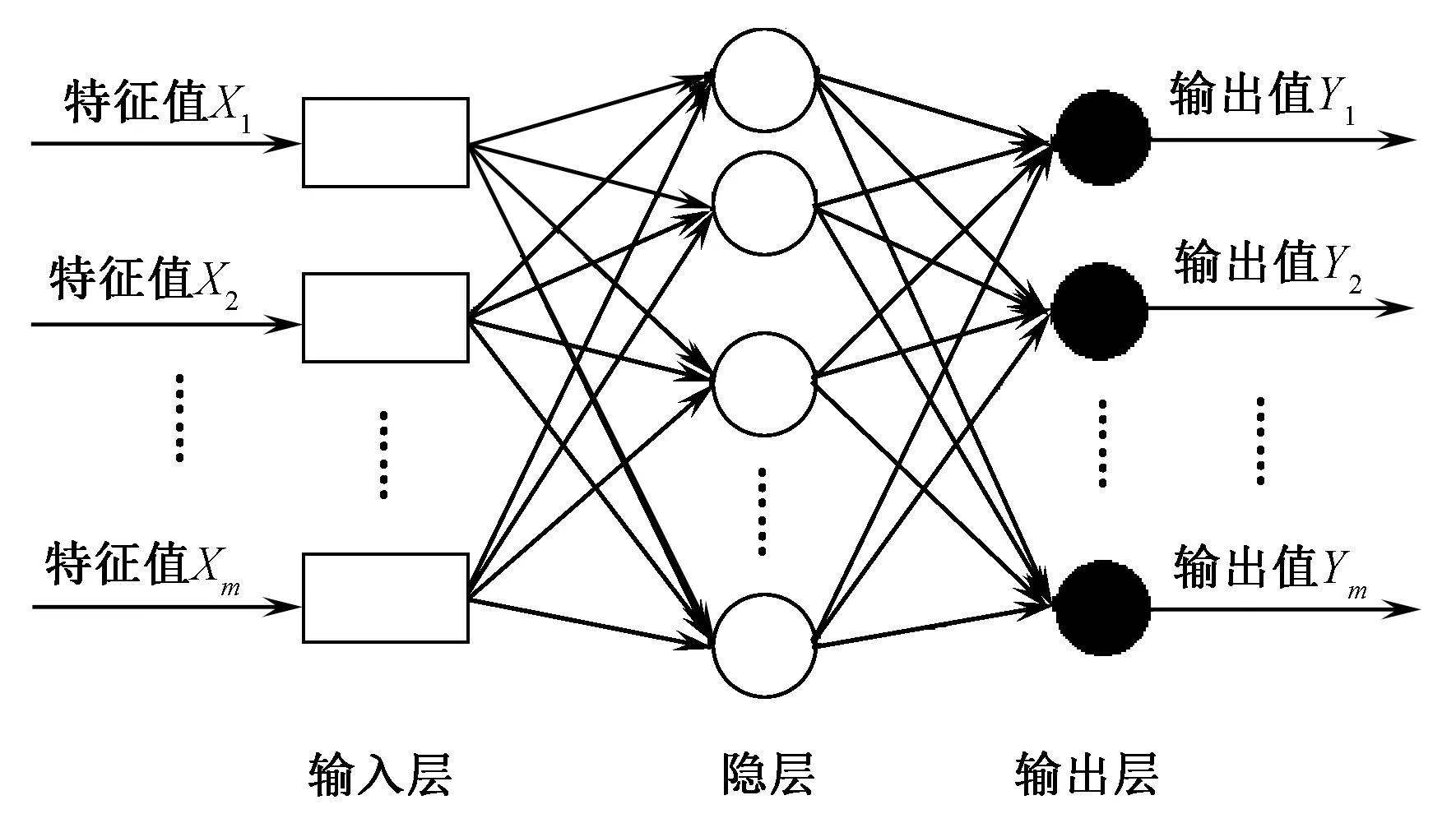
图4 BP神经网络的模型结构图Fig.4 Structure of BP neural network model

设输入节点为xl，隐层节点为ym，输出节点为zn，输入节点与隐层节点间的网络权值为wlm，阈值为θm，隐层节点与输出节点间的网络权值为vmn，阈值为θn，当输出节点的期望值为tn时，该BP神经网络模型的隐层节点的输出yl、输出节点的实际输出zm和输出节点的误差σ计算式如下所示。

(8)

(9)

(10)

在该BP神经网络模型中，输入层接受输入信息，经隐层逐层处理和信息变换后，输送到输出层。如果输出层得不到期望输出，则转入反向传播，通过信息的正向传播和误差的反向传播来不断调整网络的权值和阈值，直至网络输出的误差减少到可接受的程度，或者达到预先设定的学习次数为止。

3.2 BP神经网络的构建

3.2.1 节点数的确定

为描述缝纫试样图像的特征，实验中提取了5个特征值F1、F2、F3、F4、F5，分别表示图像灰度共生矩阵的能量、熵、对比度、相关性和小波水平细节系数。缝纫试样的平整度等级划分为1～5级，神经网络的输入层和输出层节点数均设置为5。隐层节点数可根据输入层、输出层的层数和经验式(11)确定其取值范围。

(11)

式中：m、l、n分别为隐层、输入层、输出层的节点数；c为1～10之间的整数。

由式(11)可得，隐层节点数的范围为4～13。通过设置不同的隐层节点数，在BP神经网络中训练，直至结果稳定，所得到的平均训练次数在节点数为7时趋于稳定，实验中隐层的节点数设置为7。

3.2.2 其他参数的确定

在BP神经网络中，其他参数包括激励函数、阈值、学习速率和训练次数。激励函数选择Sigmoid函数，对于多层神经网络，Sigmoid函数划分的区域是由非线性的超平面组成的区域，分类效果比线性划分准确、合理，而且网络的容错性较好。阈值的大小决定了Sigmoid函数曲线变换的梯度，本文中输入、输出函数的阈值θm和θn的初始值均选择为0.3，学习速率为0.06[16]，设置神经网络的训练次数为 2 000，训练所要达到的精度为1×10-4。

3.3 BP神经网络的训练

根据确定的BP神经网络的参数，借助现有的函数在MatLab程序下实现BP神经网络的构建。对于BP神经网络的训练，具体的实现步骤如下：1)初始化神经网络，设置确定好的各项参数，其余的参数选择默认值；2)提取图像的特征值作为训练样本，与相对应的期望输出的等级输入到网络中；3)反复训练，调整网络的权值和阈值，直至网络输出误差的平方和最小，或者达到设定的学习次数为止。

选择每个等级5幅图像，共25幅缝纫试样图像，分别提取其特征值作为训练集。图5示出神经网络在训练过程中均方误差的收敛过程。从图中可看出，训练收敛时的训练次数为265，说明构建的神经网络具有较好的预测能力。

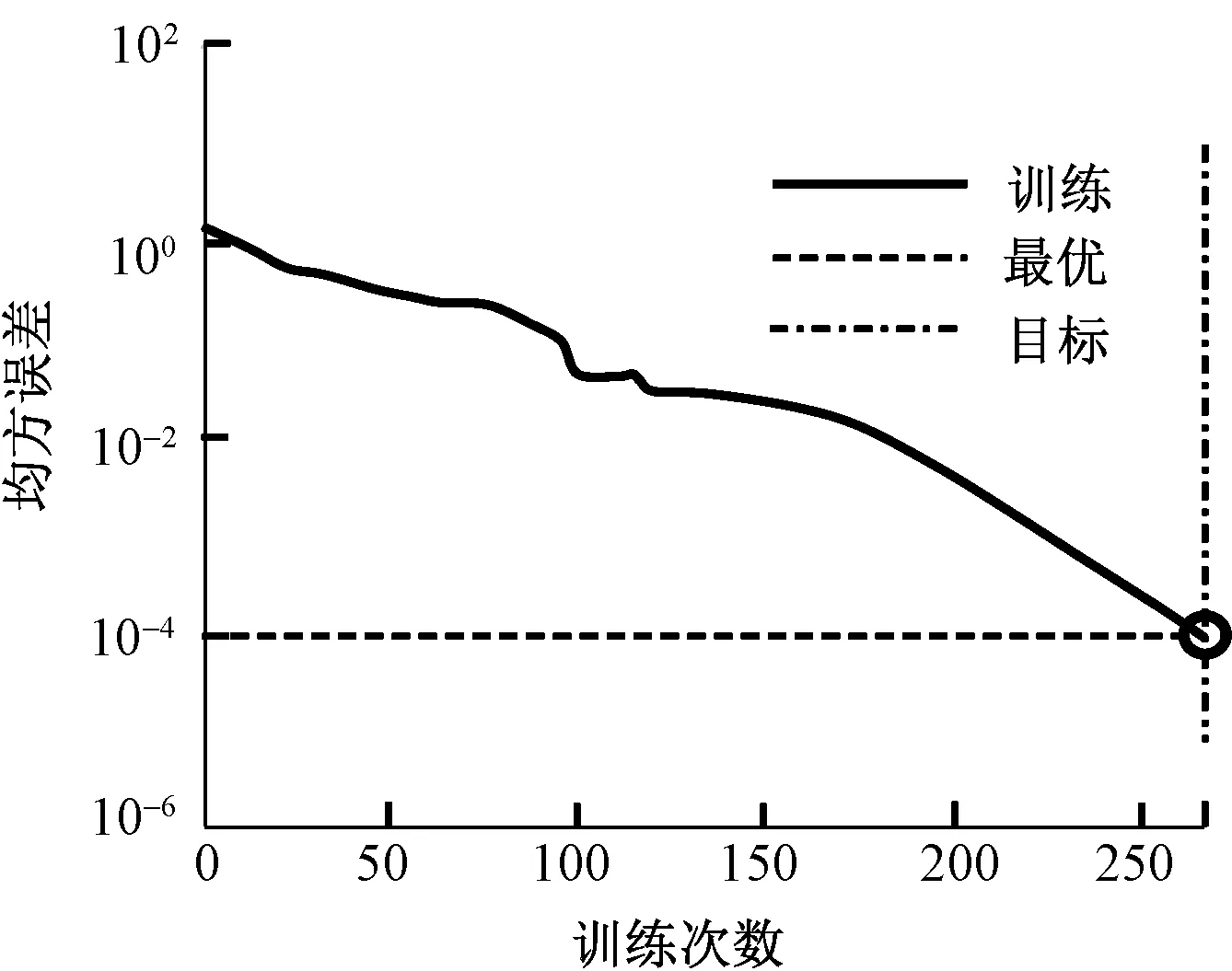
图5 神经网络的误差收敛过程Fig.5 Error convergence process of neural network

4 评估结果与分析

为验证上述算法的正确性，采集另外25幅标准缝纫试样图像作为预测样本，提取其特征参数，输入到构建的神经网络中进行识别分类。通过上述算法提取的特征参数以及神经网络自动评估产生的等级G1与标准试样的等级G2的对比结果如表1所示。

从表1中的对比结果可看出，通过神经网络自动评估产生的等级G1与标准试样的等级G2完全吻合，分类正确率达到了100%。这说明提取的5个特征值可表征不同的缝纫试样等级，可用于织物缝纫平整度的自动评估。

为验证算法的优越性，将本文算法中灰度共生矩阵及小波特征的分类结果与前人所采用方法小波特征[4]、灰度共生矩阵特征[5]的结果相对比，结果如表2所示。从表中可看出，灰度共生矩阵及小波特征综合了二者的特征信息，与单独的灰度共生矩阵特征、小波特征相比，正确率较高，具有较好的分类效果。

5 结束语

通过采集标准织物缝纫试样图像并进行预处理，运用灰度共生矩阵和小波分析相结合的方法，提取图像的5个特征参数作为特征值，输入到BP神经网络中进行分类和识别，实现织物缝纫平整度的自动评估。本文提出的算法将图像的全局信息和局部细节信息相结合，可更为全面地表征不同等级的图像信息，具有较高的分类正确率。

表1 特征参数和缝纫平整度等级Tab.1 Characteristic parameters and grades of seam-puckering

表2 不同方法分类结果的对比Tab.2 Comparison of classification results among different methods

为得到稳定的分类结果，目前在分类识别时，作为训练集和预测集的图像，均是标准的缝纫图像，但是在实际的缝纫试样图像中，由于光照条件、面料种类和织物组织结构等因素的影响，使得实际的缝纫试样在评估时存在较多的不确定性；因此，根据现有的方法，对实际的缝纫试样图像的评估将是进一步的研究方向。

FZXB

[1] MARIOLIS I G, DERMATAS E S. Automatic classification of seam pucker images based on ordinal quality grades[J]. Formal Pattern Analysis & Applications, 2011, 16(3): 447-457.

[2] MARIOLIS I G, DERMATAS E S. Automated assessment of textile seam quality based on surface roughness estimation[J]. Journal of the Textile Institute, 2010, 101(7): 653-659.

[3] KANG T J, PARK C, LEE J. Evaluation of seam pucker using fractal geometry[J]. Journal of the Textile Institute, 1999, 90(4): 621-636.

[4] 李艳梅, 张渭源. 小波分析在织物缝纫平整度客观评价中的应用[J].纺织学报, 2009, 30(10): 115-118. LI Yanmei, ZHANG Weiyuan. Application of wavelet analysis in evaluation on seam pucker of fabrics[J]. Journal of Textile Research, 2009, 30(10): 115-118.

[5] MAK K L, LI Wei. A Neural network approach to objective evaluation of seam pucker[C]//Proceedings of the World Congress on Engineering. London:[s.n.], 2007: 2-4.

[6] 杨晓波. 基于模糊模式识别的织物平整度等级评定[J].纺织学报, 2005, 26(6): 15-17. YANG Xiaobo. Fabric smoothness grade assessment based on fuzzy pattern recognition[J]. Journal of Textile Research, 2005, 26(6): 15-17.

[7] 潘永惠, 包芳, 王士同. 基于改进RBF网络的缝纫平整度模糊辨识系统[J].纺织学报, 2008, 29(3): 76-79. PAN Yonghui, BAO Fang, WANG Shitong. A fuzzy evaluation system of garment seam smoothness based on improved RBF network[J]. Journal of Textile Research, 2008, 29(3): 76-79.

[8] FAN J T, LU D, MACALPINE J M K, et al. Objective evaluation of pucker in three-dimensional garment seams[J]. Textile Research Journal, 1999, 69(7): 467-472.

[9] KOEHL L, MIOU J C, ZENG X. Selecting Relevant Features From Fabric Images for Automated Quality Control of Seam Pucker Using Data Analysis and Human Experts Grading[M]. Berlin Heidelberg: Springer, 2007: 39-54.

[10] KANG T J, KIM S C, SUL I H, et al. Fabric surface roughness evaluation using wavelet-fractal method: part I: wrinkle, smoothness and seam pucker[J]. Textile Research Journal, 2005, 75(11): 751-760.

[11] HARALICK R M, SHANMUGAM K, DINSTEIN I. Textural features for image classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1973, 3(6): 610-621.

[12] 高士忠. 基于灰度共生矩阵的织物纹理分析[J].计算机工程与设计, 2008, 29(16): 4385-4387. GAO Shizhong. Analysis of fabric texture based on GLCM[J]. Computer Engineering and Design, 2008, 29(16): 4385-4387.

[13] 曹瑜, 涂玲, 毋立芳. 身份认证中灰度共生矩阵和小波分析的活体人脸检测算法[J].信号处理, 2014, 30(7): 831-834. CAO Yu, TU Ling, WU Lifang. Face liveness detection using gray level co-occurrence matrix and wavelets analysis in identity authentication[J]. Journal of Signal Processing, 2014, 30(7): 831-834.

[14] ULABY F T, KOUYATE F, BRISCO B, et al. Textural information in SAR images[J]. IEEE Transaction on Geoscience and Remote Sensing, 1986, 24(2): 235-245.

[15] 李艳梅, 仇晓坤, 蒋真真. 缝纫平整度客观评判模型的研究[J].丝绸, 2011, 48(4): 28-30. LI Yanmei, QIU Xiaokun, JIANG Zhenzhen. Research on objective evaluating model of seam pucker[J]. Journal of Silk, 2011, 48(4): 28-30.

[16] 卢柳叶, 张青峰, 李光录. 基于BP神经网络的遥感影像分类研究[J].测绘科学, 2012, 37(6): 140-142. LU Liuye, ZHANG Qingfeng, LI Guanglu. Image classification of remote sensing based on BP neural networks[J]. Science of Surveying and Mapping, 2012, 37(6): 140-142.

Automatic seam-puckering evaluation using image processing

ZHANG Ning, PAN Ruru, GAO Weidong

(Key Laboratory of Eco-Textiles(Jiangnan University), Ministry of Education, Wuxi， Jiangsu 214122, China)

In order to solve the problem on low-accuracy classification in objective automatic evaluation of seam-puckering, a novel method based on gray level co-occurrence matrix, wavelet analysis and back propagation(BP) network was proposed for automatic seam-puckering evaluation. Firstly, a standard seam image was captured and the gray level of the seam image was reduced to 16 level, the gray level co-occurrence matrix of the seam image in the direction of 0° and 90° were calculated and normalized, then four characteristic parameters including energy, entropy, contrast and correlation were extracted from the gray level co-occurrence matrix, and the mean values of the characteristic parameters were obtained in the direction of 0° and 90°, respectively. Meanwhile, the standard deviation of the horizontal detail coefficients of the seam image was extracted and calculated by using Haar wavelet on the sixth analysis scales. After that, five extracted characteristic parameters were input to the BP neural network for training and recognizing, and the standard seam image was evaluated. The evaluation results show that the proposed algorithm, compared with one adopting gray level co-occurrence matrix characteristic or wavelet characteristic alone, has higher correct classification rate and stable classification effect.

seam-puckering; gray level co-occurrence matrix; wavelet analysis; BP network

10.13475/j.fzxb.20160404106

2016-04-14

2016-10-19

国家博士后基金项目(2013M541602)；教育部博士点基金项目(20120093130001)；江苏省博士后基金项目(1301075C)； 2014江苏省研究生创新计划项目(KYLX_1132)；江苏高校优势学科建设工程资助项目(苏政办发[2014]37号)

张宁(1992—)，男，硕士生。研究方向为基于图像处理的织物模拟、模式识别。高卫东，通信作者，E-mail: gaowd3@163.com。

TS 941.16

A