簇绒地毯织机横移机构的谐振抑制

郗欣甫， 黄 双， 孙以泽

(东华大学 机械工程学院， 上海 201620)

簇绒地毯织机横移机构的谐振抑制

郗欣甫， 黄 双， 孙以泽

(东华大学 机械工程学院， 上海 201620)

针对簇绒地毯织机高速运行时横移机构易出现机械谐振，影响横移系统快速响应和稳定性的问题，在对横移传动机构进行理论建模的基础上设计了校正补偿装置。首先根据横移传动系统的阶跃响应情况，采用双T型陷波滤波器消除了横移传动系统的机械谐振点。然后使用预变形双线性逼近法对陷波滤波器进行离散化处理，并且与零阶保持器和一阶保持器等离散算法进行了实验对比。结果表明，双T型滤波器有效地消除了横移机构高速运行时产生的机械谐振，而且在频域特性方面，采用预变形逼近法设计的离散陷波滤波器可获得比零阶和一阶保持器更加准确的逼近效果。

横移机构； 校正补偿装置； 谐振抑制； 陷波滤波器； 离散方法

簇绒地毯产品丰富多样而且生产效率高，市场占有率相比于编织地毯占有压倒性优势。近年来国内簇绒地毯产业飞速发展，但与国外仍有较大差距。Tuftco 公司以其独有的直接高速驱动(DDHS)技术[1]将簇绒地毯织机的工作转速提升到了2 000 r/min，而国内现有的高端产品只能做到800 r/min。制约簇绒地毯生产效率和产品质量的因素主要有3个：1)耦联轴系传动系统以及机架在机器高速运行时产生的振动[2]；2)由横移传动机构引起的机械谐振和间隙振荡；3)提花系统喂纱精度以及纱线张力的控制[3-5]。近年来针对簇绒地毯织机横移系统振动抑制的问题少有研究，但是作为纺织机械制造业的共性难点，在经编机等其他纺织机械设备上已积累了大量的经验[6-7]。

在机电一体化设备中，传动部件如传动轴、滚珠丝杠、联轴器等都会有一定的弹性，当传动机构的弹性模态被激发时就会导致机械谐振[8]，不仅影响系统运行时的性能和精度，而且对生产设备产生损害，甚至产生不可挽回的损失[9]。针对机械谐振抑制的控制方法主要分为机械和电气2种控制方案。机械方案立足于机械设计，通过机构优化如动静平衡、吸能耗能、增大传动刚度等来降低谐振的影响。机械抑制方案在一定程度上能起到很好的效果，但随着控制效果和精度的提高，成本也会急速上升。电气方案又分为主动控制和被动控制2种方式。主动控制通过实时观测振动状态和环境干扰，通过特定的高级控制算法主动修改控制器参数实现有效抑制机械谐振的目标[10-11]。主动控制方式不依赖于外部环境的干扰，有很强的稳定性，控制的效果取决于控制算法的选择和控制器的设计[12-13]。被动控制是针对特定的谐振点设计陷波滤波器以达到消除谐振的目的，这种方法控制参数相对较少，易实现[14]。目前商用伺服系统大都采用被动控制方案将单个或多个陷波滤波器设置于速度环和电流环之间消除特定的谐振点，这样不仅可降低成本而且也能够达到令人满意的效果[8, 15]。

1 簇绒地毯织机横移机构系统

簇绒地毯织机横移机构主要由伺服电动机、联轴器、齿轮、滚珠丝杠和直线导轨组成，主要参数相关定义和数值为：电枢电感L=0.6 H，电枢电阻R=1Ω，转子转动惯量J1=10-6kg·m2/rad，转子阻尼系数D1=10-5N·m·s /rad，电机反电动势系数Ke=0.186 V·s /rad，电机转矩常数Kt=0.4 N·m/A，传动比N=9，传动机构等效弹性系数K=0.012 N·m/rad，传动机构等效阻尼系数D12=0.15 cN·s /rad，负载等效转动惯量J2=0.8 g·m2/rad，负载等效阻尼系数D2=0.004 N·m·s/rad。系统简图如图1所示。

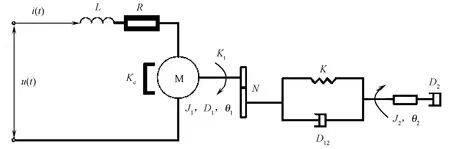
注：u(t)为伺服电动机电枢电压；i(t)为电动机电枢电流；θ1为电动机转子的旋转角度；θ2为负载旋转角度；M为电动机。图1 簇绒地毯织机横移机构等效模型Fig.1 Reduced model of shogging mechanism in tufting carpet loop

根据横移机构的等效模型，系统参数有如下关系：

(1)

根据式(1)建立系统的状态方程。设状态变量x为

(2)

x5=θ2

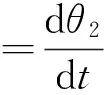
则状态方程为

(3)

其中:A为系统状态系数矩阵；B为系统控制系数矩阵；C为输出状态系数矩阵；u为控制向量；y为输出向量。

(4)

根据系统的状态方程式(3)、(4)和表1中的数值，绘制横移传动系统伯德图(Bode)如图2所示。

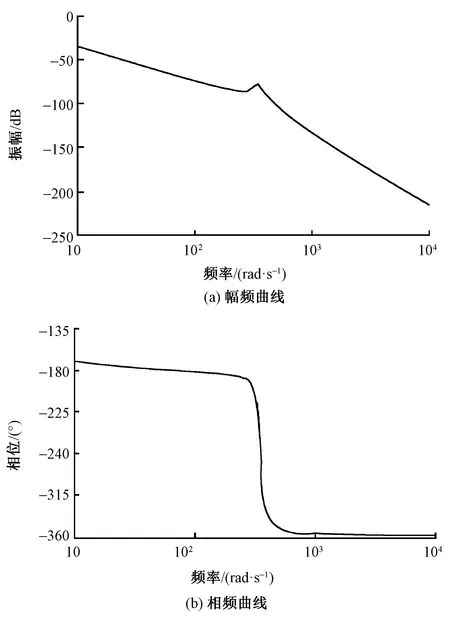
图2 横动机构系统Bode图Fig.2 Bode chart of shogging mechanism. (a)Frequency-amplitude curve; (b)Phase-amplitude curve

由图2可清楚地得到横移传动系统的谐振频率为351rad/s，即当系统运行在谐振频率点时设备会产生共振，影响设备的正常运行。

2 校正补偿装置设计

本文通过超前校正装置来增大系统相角裕度，改善其稳定性，并且可提高截止频率增强系统的快速性。超前网络的传递函数Gj(s)为

(5)

式中：K为补偿装置增益；τ1、τ2、T1、T2为校正网络的时间常数；s为复变数。

根据工作要求设定系统阶跃响应时间为0.6 s，并且超调量不得大于5%。调用MatLab函数looptune()，可得到式(6)：

(6)

将式(6)添加到系统，并验证校正后系统阶跃响应的各项指标是否保持在允许范围之内。图3示出系统校正前后的阶跃响应。由图可知，校正后系统响应速度明显提升，而且系统超调量控制在允许误差范围内，与校正前相比更加稳定。

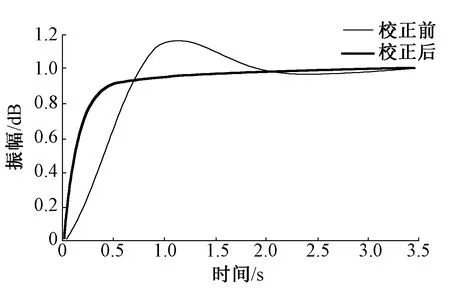
图3 系统校正前后的阶跃响应Fig.3 Step response of system before and after correction

3 双T型陷波滤波器设计

根据横移传动系统的谐振表现，选择二阶传递函数GN(S)描述双T型陷波滤波器，如式(7)所示。

(7)

式中：ζ1、ζ2为陷波滤波器阻尼系数；ωn为系统自然振荡角频率，rad/s。

依照工程经验设定系统穿越频率为50rad/s，在中频段的斜率为-30dB/(rad·s-1)，并以此整定陷波滤波器的参数，同样采用MatLab工具箱中looptune()函数进行求解，结果如式(8)所示。

(8)

图4示出了系统在配置陷波滤波器前后的阶跃响应曲线，图5示出了相应的Bode图。由图可看出，陷波滤波器的加入在有效消除谐振点的同时也改善了系统的动态性能。

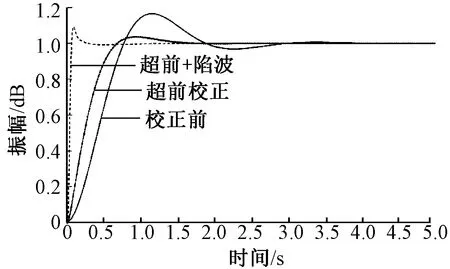
图4 系统谐波抑制前后的阶跃响应Fig.4 Step response of the system before and after resonance suppression

图5 系统谐波抑制前后的Bode图Fig.5 Bode chart of system before and after resonance suppression. (a)Frequency-amplitude curve; (b)Phase-amplitude curve

4 陷波滤波器的离散方法

双线性逼近法(Tustin法)s域和z域的关系如式(9)所示。

(9)

为使Tustin法精确地逼近谐振点，可采用预变形的方式对Tustin法针对特定的频率点进行修正[16]，关系式如式(10)所示。

(10)

选用常用的零阶保持器、一阶保持器和预变形Tustin法对陷波滤波器进行离散化，通过计算仿真如图6所示。采用零阶保持器和一阶保持器都会存在一定的增益和相位裕量畸变，而预变形双线性逼近法在频域效果上更加贴近于连续陷波滤波器的控制效果。

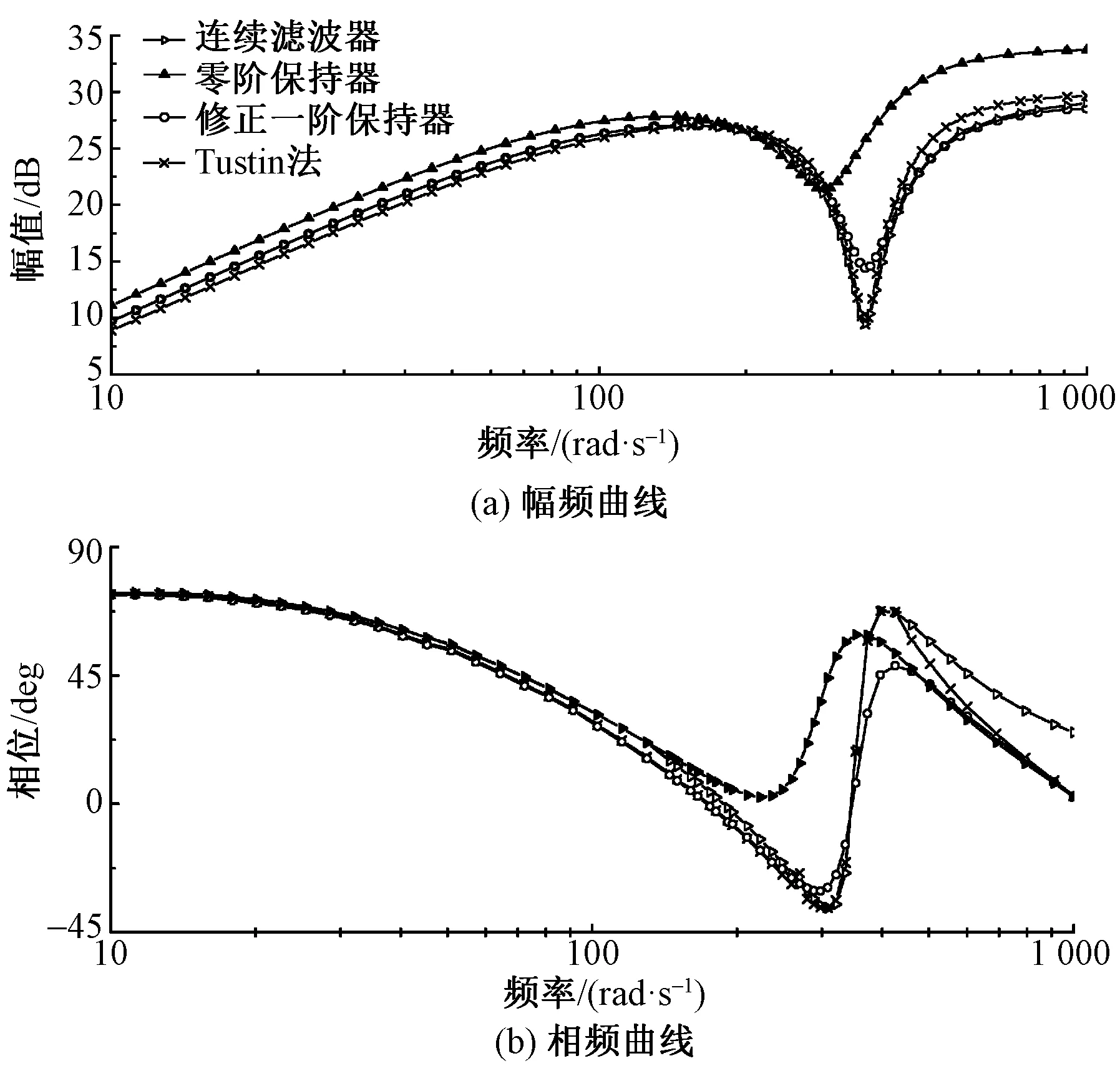
图6 不同离散方法对陷波滤波器的影响Fig.6 Influence of different discretization methods on notch filter. (a)Frequency-amplitude curve; (b)Phase-amplitude curve

5 结 论

1)簇绒地毯织机横移系统通过校正补偿可提高系统的快速响应性和稳定性。

2)采用不同的离散方法对陷波滤波器的实际增益和相位会产生较大影响，所以要针对实际应用要求选择恰当的离散方法以达到最佳控制效果。

3)对簇绒地毯织机横移系统建模，添加校正装置和陷波滤波器，可有效地提高织机横移控制系统的动态性能，并为系统设计提供理论参考。

FZXB

[1] MORGANTE M R, BEATTY P E. Tufting machine head shaker：USA,US7578249[P]. 2009-06-01.

[2] 丁彩红, 杨延竹, 孙以泽. 地毯簇绒机械轴系动力学问题研究的现状与展望[J]. 纺织学报, 2007,28(8): 120-123. DING Caihong, YANG Yanzhu, SUN Yize. State and outlook of research on shafting dynamics of carpet tufting machine[J]. Journal of Textile Research, 2007,28(8): 120-123.

[3] 丁彩红, 唐军. 牵引罗拉稳定纱线张力的作用机制[J]. 纺织学报, 2010，31(2): 110-114. DING Caihong, TANG Jun. Mechanism analysis of yarn tension stabilization using pulling rollers[J]. Journal of Textile Research, 2010,31(2): 110-114.

[4] 夏胜华, 孙以泽, 孟婥, 等. 簇绒地毯织机提花装置的绕纱动态张力分析[J]. 纺织学报, 2015,36(7): 136-141. XIA Shenghua, SUN Yize, MENG Zhuo, et al, Dynamic tension analysis on winding yarn in jacquard device of tufting carpet machine[J]. Journal of Textile Research, 2015,36(7): 136-141.

[5] 徐洋, 孙志军, 孟婥, 等. 地毯簇绒系统纱线张力建模与分析[J]. 纺织学报, 2010,31(12): 116-121. XU Yang, SUN Zhijun, MENG Zhuo, et al. Modeling and analysis on yarn tension of carpet tufting ma-chine[J]. Journal of Textile Research, 2010,31(12): 116-121.

[6] 刘念, 夏风林, 张琦, 等. 经编机梳栉横移机构的动力学分析[J]. 纺织学报, 2012,33(11): 121-126. LIU Nian, XIA Fenglin, ZHANG Qi, et al. Dynamic analysis of shogging motion mechanism of guide bar on warp knitting machine[J]. Journal of Textile Research, 2012,33(11): 121-126.

[7] 张琦, 夏风林, 刘念, 等. 经编机梳栉的横移振动分析[J]. 纺织学报, 2013,34(7): 121-125. ZHANG Qi, XIA Fenglin, LIU Nian, et al. Analysis of shogging motion vibration of guide bars on warp knitting machines[J]. Journal of Textile Research, 2013,34(7): 121-125.

[8] ELLIS G, LORENZ B D. Resonant load control methods for industrial servo drives[C]//OKYAY Kaynak. IEEE Industry Applications Conference. Istanbul: IEEE, 2000.

[9] SZABAT K, ORLOWSKA-KOWALSKA T. Application of the kalman filters to the high-performance drive system with elastic coupling[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4226-4235.

[10] KNYCHAS S, DERUGO P, SZABAT K. Damping of the torsional vibration using adaptive fuzzy control system with different recurrences[C]//KNYCHAS S. Industrial Electronics (ISIE), 2014 IEEE 23rd International Symposium on. Turkey: [s.n.].2014.

[11] PAJCHROWSKI T, ZAWIRSKI K, NOWOPOLSKI K. Neural speed controller trained online by means of modified RPROP algorithm[J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 560-568.

[12] HACE Ales, JEZERNIK Karel, SABANOVIC Asif, et al. SMC with disturbance observer for a linear belt drive[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3402-3413.

[13] PETER K I B. Robust output-feedback H∞ control With a nonlinear observer for a two-mass system[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 8.

[14] MURPHY B R, WATANABE I. Digital shaping filters for reducing machine vibration[J]. IEEE Transactions on Robotics and Automation, 1992, 8(2): 285-289.

[15] HSU W C, LAI C L, HSU P L. A novel design for vibration suppression for lightly-damped servo control systems[C]//WANG Zidong. 8th Asian Control Conference. Taiwan: IEEE, 2011:251-256.

[16] KORLINCHAK C, COMANESCU M. Discrete time integration of observers with continuous feedback based on Tustin′s method with variable prewarping[C]//LING Nam. 6th IET International Conference on Power Electronics. Xining: IET, 2012:161-161.

Resonance suppression strategy of shogging mechanism in tufting carpet loom

CHI Xinfu, HUANG Shuang, SUN Yize

(College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

Aiming at the problem that the mechanical resonance which influenced the responsiveness and stability of the shogging mechanism was easily induced during the high speed operation of the shogging mechanism on tufting carpet loom, the paper designed the compensation device based on a theoretical model of the shogging mechanism. Firstly, the paper adopted a double T type notch filter to eliminate mechanical resonance points of the shogging driving system, based on the s step response. And then the paper used the Tustin prestressing bilinear approximation method to perform discretization on the notch filter, and compared with the discretization algorithms such as a zero order holder and a first order holder. The results show that the double T type notch filter can well inhibit the mechanical resonance during high speed operation of the shogging mechanism, and the discrete notch filter designed by the Tustin prestressing bilinear approximation method can achieve more accurate approximation effect of the frequency domain characteristics than the zero order holder and the first order holder.

shogging mechanism; compensation device; resonance inhibition; notch filter; discrete method

10.13475/j.fzxb.20160303805

2016-03-21

2016-07-25

国家自然科学基金项目(51375084, 51675094)

郗欣甫(1988—)，男，博士生。主要研究方向为纱线力学、多电动机协同控制。孙以泽，通信作者，E-mail：sunyz@dhu.edu.cn。

TS 103.3

A