番木瓜片热风微波耦合干燥条件及干燥模型建立

易 丽,杨 薇,王 晨

(昆明理工大学现代农业工程学院,云南昆明 650500)

番木瓜片热风微波耦合干燥条件及干燥模型建立

易 丽,杨 薇*,王 晨

(昆明理工大学现代农业工程学院,云南昆明 650500)

为研究番木瓜片采用热风微波耦合干燥的干燥特性和最优工艺组合,选用自制热风微波耦合干燥系统进行实验,得出热风微波耦合干燥曲线、干燥速率曲线及最优工艺组合,并建立干燥模型。结果表明:番木瓜片热风微波耦合干燥速率经历一个短暂的加速期后较长时间处于降速期;番木瓜片热风微波耦合干燥综合效果最优的组合为:热风温度60 ℃、微波功率密度5.5 W/g、热风风速0.5 m/s,其中微波功率密度对干燥综合效果的影响起主导作用;番木瓜片热风微波耦合干燥动力学模型可用Page方程描述,即MR=exp(-0.0011T-0.0069PD+0.073t(0.0015T2-0.1993T+7.9642));番木瓜片热风微波耦合干燥有效水分扩散系数介于2.533×10-9～6.0792×10-9m2/s之间,且有效水分扩散模型为:10-10Deff=0.507T+6.72PD+10.1v-32。

番木瓜片,耦合干燥,干燥条件,干燥模型

番木瓜(Carica papaya linn)俗称木瓜、万寿果等,是典型的热带水果。番木瓜富含维生素C、木瓜蛋白酶等多种成分,具有抗癌、免疫调节、美容等功效,享有百益果王、岭南佳果等美誉[1-2]。新鲜番木瓜被采收后,水分含量很高、呼吸强度大,极易腐烂变质,加工成干制品,既可延长产品寿命,又可增加产品附加值[3]。

在保证干燥品质的前提下,降低单位能耗、缩短干燥时间是农产品干燥的一个重要研究方向。传统的热风干燥的优点是物料处理量大、设备成本低、操作简单。但缺点是易造成产品品质差、干燥速率低和能耗高[4]。微波干燥的干燥速率较快、能耗低,但物料处理量小,在干燥后期,物料表面会出现焦糊[5]。热风微波耦合干燥是热风和微波同时作用于干燥物料的干燥方法,综合了热风干燥和微波干燥的特点,能实现物料内外同时加热,大幅度缩短干燥时间,提高干燥产品品质。目前,国内外的一些学者对热风微波耦合干燥的干燥特性、工艺以及干燥动力学进行了研究。利用热风、微波和热风微波耦合干燥方法对煮熟的鹰嘴豆和大豆进行了干燥,得出热风微波耦合干燥时间最短、热风干燥时间最长,热风微波耦合干燥的体积收缩系数明显大于其它2种方法,故在干燥期间,体积收缩更快[6];采用热风和热风微波耦合干燥工艺干燥油茶籽,干燥时间比热风干燥节约近3倍,过氧化氢减少了7.46%[7];Babalis[8]等选用10个数学模型对无花果热风干燥曲线进行拟合,通过模型评价指标(决定系数R2及卡平方χ2)分别选出了不同热风温度下,最适合描述无花果热风干燥的干燥动力学模型。孙帅等[9]根据传热传质理论,建立了柱状胡萝卜内部温度数学模型和含水量分布数学模型。

虽然对农产品热风微波耦合干燥已有初步研究,但有关热风微波耦合干燥时兼顾产品品质、干燥速率、能耗的工艺参数优化和干燥数学模型研究目前尚未见报道。本研究采用自制的热风微波耦合干燥系统,以番木瓜片为原料,研究番木瓜片热风微波耦合干燥特性和干燥工艺参数,为采用热风微波耦合干燥番木瓜片提供一定依据。

1 材料与方法

1.1 材料与仪器

番木瓜 品种为“穗中红”,昆明市呈贡区当地市场。大小均匀、无机械损伤,果皮转黄率为60%的果实,番木瓜初始湿基含水率的平均值为88.06 g/100 g(对应干基含水率为737.52 g/100 g)。

热风微波耦合干燥系统 实验室自制,见图1,此装置由热风干燥装置和微波发生装置组成[10];色彩色差计 CR-400型,柯尼卡美能达公司;电子分析天平 BL310型,德国赛多利斯集团;恒温水浴锅 HH-S系列,江苏金坛大地自动化仪器厂。

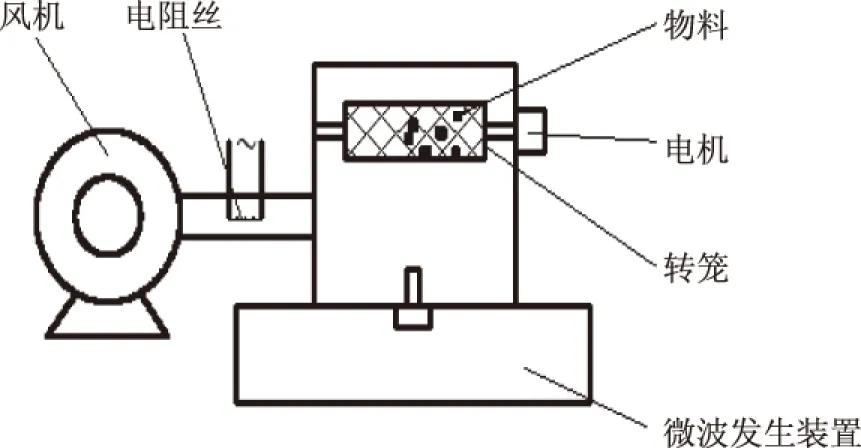
图1 热风微波耦合干燥系统示意图Fig.1 Schematic view of coupled hot air and microwave drying system

1.2 实验方法

含水率:依据GB 5009.3-2010中的直接干燥法[11]测定。

原料处理:将削皮、去瓤、去籽后的番木瓜,沿轴向切成厚度为5 mm的薄片,称取150 g左右的番木瓜片放入自制的转笼中,随后将其放入干燥室中进行干燥。

干燥终止条件:每隔3 min测一次质量,干燥至番木瓜干基含水率小于安全含水率(8 g/100 g)[12];每组实验重复3次,实验结果取3次的平均值。

1.2.1 热风微波耦合干燥

1.2.1.1 热风微波耦合干燥单因素实验 为了研究热风温度、微波功率密度、热风速度3个因素分别对番木瓜片热风微波耦合干燥特性及干燥动力学的影响,按表1进行单因素实验,干燥曲线及干燥速率曲线见图2、图3、图4。

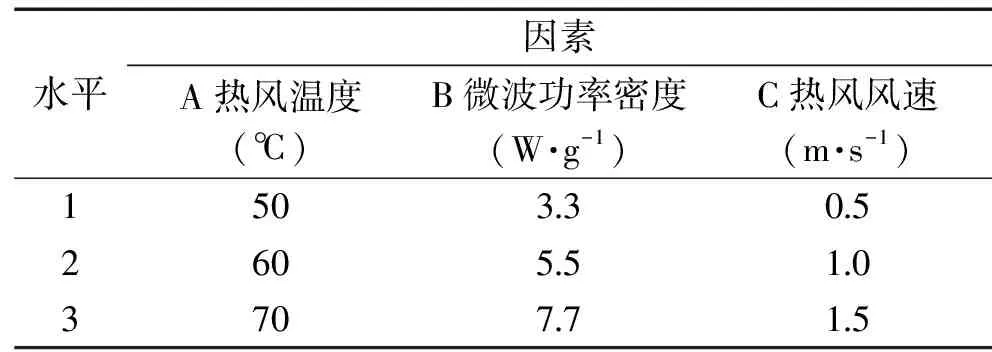
表1 热风微波耦合干燥单因素实验方案

1.2.1.2 热风微波耦合干燥正交实验 选取热风温度、微波功率密度、热风风速3个因素进行L9(34)的正交实验,实验因素水平由单一热风干燥和微波干燥实验确定,实验安排及结果见表2。微波功率密度是单位质量的平均微波功率,由式(1)计算[13]:

式(1)

式中:PD为微波功率密度,W·g-1;P1为微波功率,W;m1为初始物料质量,g。

1.3 评价指标

不同实验干燥完成后均取3个平行样,以平均值计算评价指标值。

1.3.1 色泽 采用色差计测定。

1.3.2 复水比 将称好的一定质量的样品放入40 ℃恒温的蒸馏水中浸泡30 min,之后取出沥干20 min,称取其样品的质量[14]。产品复水比计算公式如下:

RR=Mf/Mg

式中:RR为复水比;Mf为产品复水沥干后的质量,g;Mg为复水前产品的质量,g。

1.3.3 干燥速率 样品干基含水率依据GB 5009.3-2010中的直接干燥法[11]测出,干燥速率计算公式如下[15]:

式中:U为t时刻样品干燥速率,(g/100g)/min;Mt,Mt-1为t,t-1时刻样品干基含水率,g/100g;t为干燥时间,min。

1.3.4 单位能耗 单位能耗以每组实验的电能表计量数为准,计算公式如下[15]:

N=(P·t)/m2

式中:N为单位能耗,kJ·kg-1;P为干燥消耗的总功率,kW,其中:P=P1+P2+P3,P1为微波干燥消耗的功率,kW;P2为热风干燥消耗的功率,kW;P3为风机消耗的功率,kW。t为总干燥时间,s;m2为去除水分的质量,kg。

1.3.5 综合加权评分法

1.3.5.1 各指标权重系数的确定 由熵值法确定各指标权重系数[16],求得总色差值、复水比、干燥速率、单位能耗的权重依次为0.35、0.19、0.28、0.17。

1.3.5.2 计算综合加权评分值 每次实验的综合加权评分值可由下列公式计算得出:

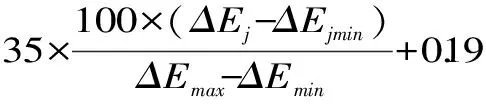
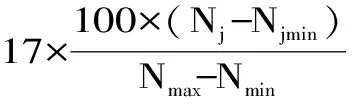
式中:j=1,2,…,9;yj为第j号实验的综合加权评分值;ΔEj为第j号实验的总色差值;ΔEjmin,ΔEjmax为总色差值的最小值、最大值;RRjmax为复水比的最大值;RRj为第j号实验的复水比;(RRjmax-RRj)min,(RRjmax-RRj)max为数据RRjmax-RRj中的最小值、最大值;Ujmax为干燥速率的最大值;Uj为第j号实验的干燥速率;(Ujmax-Uj)min,(Ujmax-Uj)max为数据Ujmax-Uj中的最小值、最大值;Nj为第j号实验的单位能耗;Njmin,Njmax为单位能耗的最小值、最大值。

1.4 干燥动力学模型

1.4.1 选择数学模型 选用Newton模型[17]:MR=exp(-kt)、Page模型[18]:MR=exp(-ktn)、Henderson and Pabis模型[19]:MR=a·exp(-kt)3个应用较广泛的薄层干燥模型[20]来描述番木瓜片的干燥特性,并对其干燥曲线进行拟合,从中选出最适合番木瓜片热风微波耦合干燥的干燥动力学模型。模型中:a、b、n、k均为待定系数;t为干燥时间,min;MR为水分比,计算公式如下:

式中:Mt为物料在t时刻的干基含水率,g/100 g;M0为物料的初始干基含水率,g/100 g;Me为物料的平衡干基含水率,g/100 g。由于Me实验室不易获取,且其值相对于Mt、M0很小,故可忽略其影响,则水分比MR的计算公式可简化为[21]:

1.4.2 干燥动力学模型评价标准 在选择最优干燥动力学模型及判断模型优劣时,有三个评价标准:决定系数R2、卡平方χ2及均方根误差RMSE[22]。其计算公式如下[15]:

式中:MRexp,i是实验测得的水分比;MRpre,i是模型预测的水分比;N是实验数据个数;k是所选用干燥动力学模型中参数的个数。

1.5 有效水分扩散系数

Fick第二定律的数值解为[23]:

式中:Deff为有效水分扩散系数,m2·s-1;δ为物料厚度,m;n=0,1,2,…

对于长时间的干燥,取n=0,并将上述方程取对数得线性方程[24]:

(2)

根据上述线性方程(即水分比MR的对数与相对应时间t的直线方程)中表示的斜率求得有效水分扩散系数Deff。

2 结果与分析

2.1 热风微波耦合干燥曲线及干燥速率曲线

图2 不同热风温度下番木瓜片热风微波耦合干燥曲线及干燥速率曲线Fig.2 Combined microwave-convective hot air drying curve and drying rate curves of carica papaya slices with different hot-air temperatures注：功率密度3.3 W/g、风速1.0 m/s。

在不同的热风温度、微波功率密度和热风速度单因素影响下,番木瓜片的水分比随时间的变化曲线分别如图2a、图3a和图4a所示;番木瓜的干燥速率随含水率(干基)的变化曲线见图2b、图3b和图4b。从图2a、图3a和图4a中可以看出,随着热风温度的升高、微波功率密度的增大、热风速度的增加,番木瓜片完成干燥的时间逐渐缩短。由图2b、图3b和图4b可以看到,番木瓜片热风微波耦合干燥阶段主要为降速期,加速期较短,几乎没有恒速期。这表明番木瓜热风微波耦合干燥主要由内部水分扩散控制,故本研究对其水分扩散系数及模型进行了探讨。

表2 正交实验安排及结果

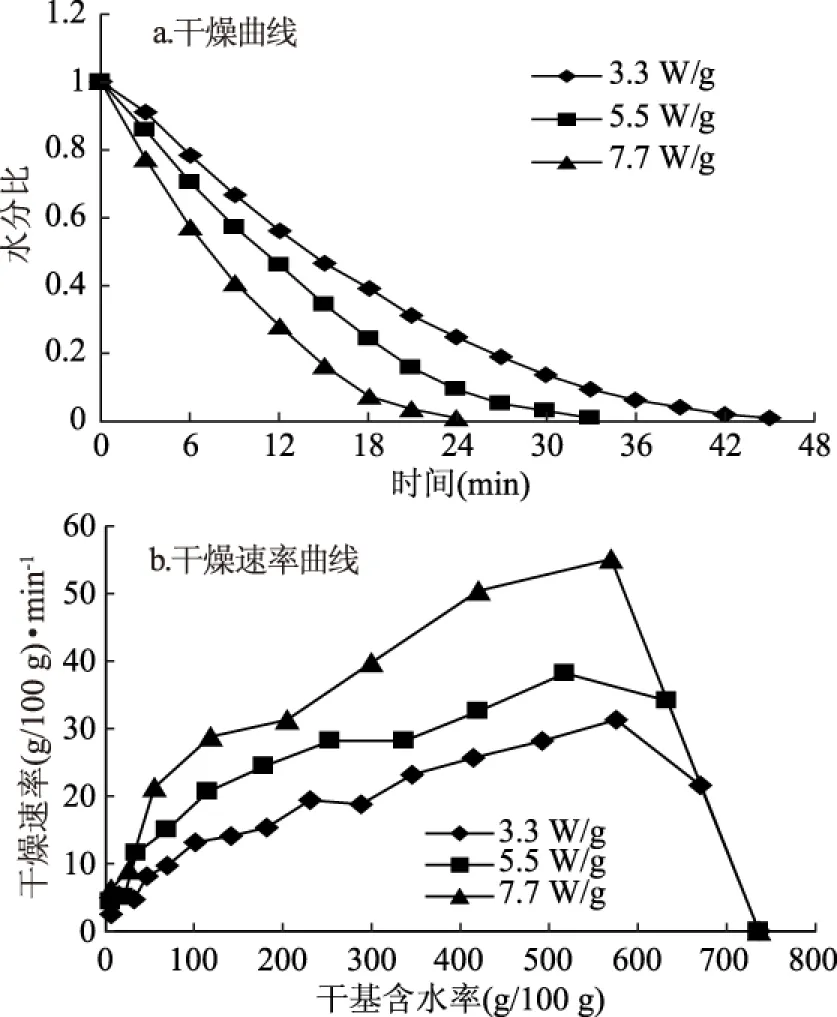
图3 不同微波功率密度下番木瓜片热风微波耦合干燥曲线及干燥速率曲线Fig.3 Combined microwave-convective hot air drying curve and drying rate curve of carica papaya slices with different microwave power densities注：温度60 ℃、风速1.0 m/s。

图4 不同热风风速下番木瓜片热风微波耦合干燥曲线及干燥速率曲线Fig.4 Combined microwave-convective hot air drying curve and drying rate curve of carica papaya slices with different hot-air velocities注：温度60 ℃、功率密度3.3 W/g。

2.2 热风微波耦合干燥最优工艺组合

2.2.1 各因素对干燥综合效果的方差分析 由表2和表3中可知,干燥综合效果最佳的组合为A2B2C1,即热风温度为60 ℃、微波功率密度为5.5 W/g、热风风速为0.5 m/s;同时,各因素对干燥综合效果的影响作用依次为:B>A>C,即微波功率密度对实验结果的影响最大,其次是热风温度,热风风速的影响最小。

表3 实验结果方差分析

2.2.2 最优方案的验证实验 按番木瓜片热风微波耦合干燥的最优方案A2B2C1进行实验,得出在最优组合条件下,产品的总色差值为13.36、复水比为4.15、单位能耗为12388.16 kJ/kg、干燥速率为26.34(g/100 g)/min,与表2中的最小总色差值12.91、最大复水比4.29、最小单位能耗13768.84 kJ·kg-1、干燥速率为30.46(g/100 g)/min相比,总色差值、复水比及干燥速率指标值相接近,且单位能耗更低。说明正交实验所得到的最优水平组合是可信的。

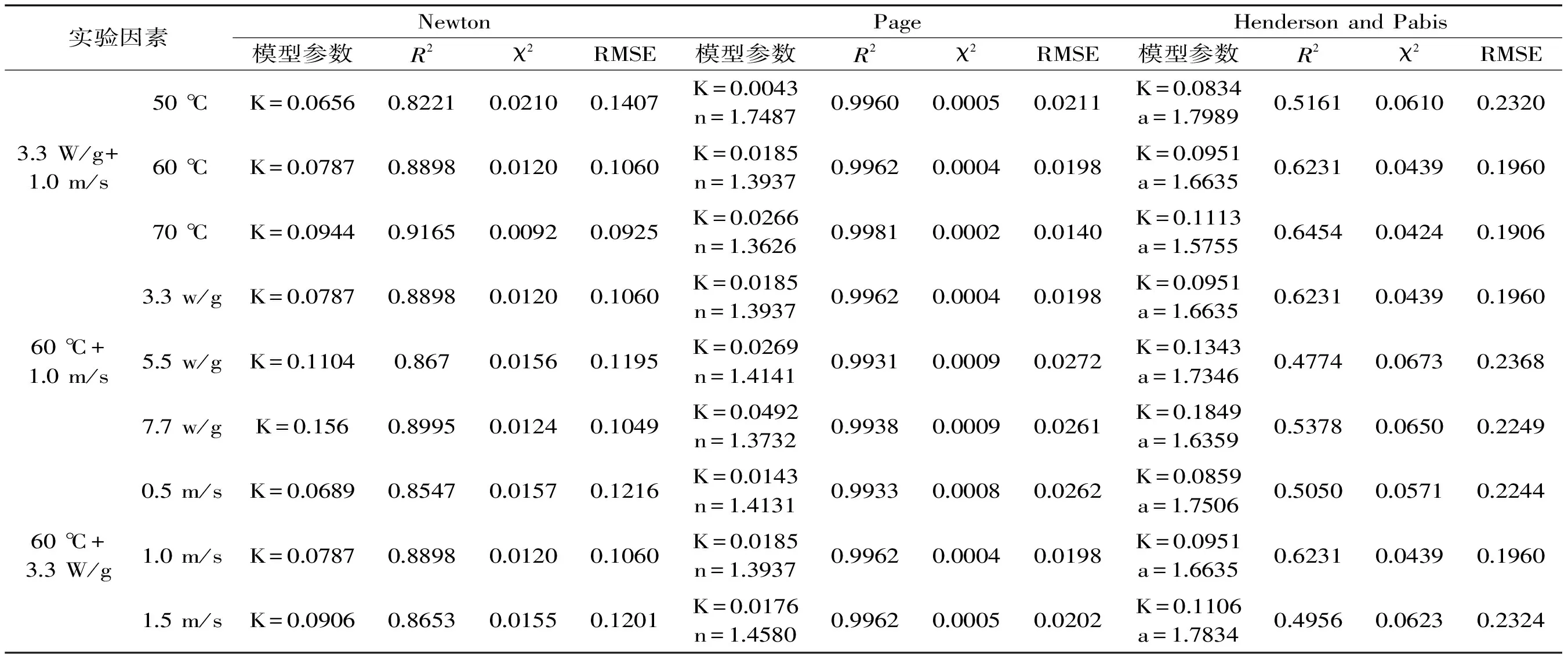
表4 3种模型在不同热风微波耦合干燥条件下的数据分析结果

2.3 热风微波耦合干燥动力学模型

对1.4.1中3种干燥动力学模型表达式进行线性化处理,结果如下:

Newton:ln(MR)=-kt

Page:ln[-ln(MR)]=lnk+nlnt

Henderson and Pabis:ln(MR)=lna-kt

根据实验数据,分别作出lnMR-t和ln(-ln(MR))-t的关系曲线图,并进行拟合,拟合的结果如表5所示。

R2越大且越接近1,说明回归关系越显著,χ2、RMSE越小,表示回归方程的预测精度越高。由表4可知,Page模型的决定系数R2最高,在0.9931～0.9981之间,χ2值最小,在0.0009～0.0002之间,RMSE值最小,在0.0262～0.0140之间,故Page模型对番木瓜片热风微波耦合干燥所得数据的拟合最优。同时,从表5可以看出,在不同的热风温度(T/℃)、微波功率密度(PD/W·g-1)及热风风速(v/m·s-1)条件下,Page模型中参数k和n的值也随之发生变化,因此,干燥常数k和n是T、PD及v的函数。根据实验数据,用SPSS软件对k和n进行回归分析并剔除其影响不显著的因素,得到参数的表达式:

k=0.0011T+0.0069PD-0.073R2=0.9599

n=0.0015T2-0.1993T+7.9642R2=0.9618

分别对所求的回归方程进行显著性分析,在α=0.01的显著水平下,参数k、n的F值分别为71.9、75.56,均大于F0.01(2,6)=10.9,表明T、PD对参数k影响非常显著,T对参数n影响非常显著。从而验证了模型的精确性及可信度。将k,n代入Page模型中,得到番木瓜片热风微波耦合干燥动力学方程为:

MR=exp(-0.0011T-0.0069PD+0.073t(0.0015T2-0.1993T+7.9642))

式(3)

式(3)给出了番木瓜片干燥过程中水分比随温度T、微波功率密度PD、干燥时间t的变化关系。在指定的热风温度及微波功率密度下,通过干燥时间,能预测番木瓜干燥过程中的水分比,在理论上描述了干燥的过程,在实际生产中,能为干燥过程提供一种控制依据。

表5 热风微波耦合干燥有效水分扩散系数

2.4 热风微波耦合干燥有效水分扩散系数及模型

有效水分扩散系数能够描述物料水分内在的传质性能,也能决定水分的扩散特性。Fick第二定律被广泛的用于描述水分扩散过程[25-26]。本实验假定物料为大平板且物料初始湿含量分布均匀、水分沿物料内部厚度方向一维等温扩散、水分迁移中物料无体积变化、物料内部对水分的运动阻力可以忽略,仅仅考虑物料表面边界层和干燥介质之间水分迁移的阻力,故Fick第二定律的数值解可由公式(2)求得。将实验数据代入式(2),通过线性拟合,求出有效水分扩散系数Deff,见表5。

由表5可知,番木瓜片在热风微波耦合干燥方法下的有效水分扩散系数Deff值介于2.533×10-9～6.0792×10-9m2/s之间,该结果与Madamba等[27]测得的食品物料干燥过程中有效扩散系数10-9～10-11m2/s相吻合。同时,由表5可以看到,有效水分扩散系数Deff随干燥因素的变化而变化。根据表5前3列数据作出Deff与热风温度T的散点图、根据表5中间3列数据作出Deff与微波功率密度PD的散点图、根据表5最后3列数据作出Deff与热风风速v的散点图,发现均呈明显的线性关系。将Deff与T、PD和v用SPSS软件进行多元回归分析,得到Deff的回归方程为:

10-10Deff=0.507T+6.72PD+10.1v-32

式(4)

回归方程决定系数为R2=0.9949,修正后的决定系数为0.9919;对回归方程进行了F检验,F尾概率3.75×10-6<0.01,故有效水分扩散系数Deff与T、PD、v之间的线性关系非常显著,从而验证了回归方程的可信度。

由回归方程(4)可知,在热风微波耦合干燥条件下,Deff随着热风温度、微波功率密度、热风风速的增大而增大。当PD和v一定时,T越高,Deff越大,这表明物料外部温度增加时,物料内部温度也随之提高,从而造成蒸汽压梯度使湿分扩散到表面并同时使液体湿分迁移;当T和v一定时,PD越大,Deff越大,因为在较大的微波功率密度下,物料吸收微波能,迅速产热,蒸汽压增大,从而导致内部水蒸汽快速扩散至表面;当T和PD一定时,v增加,Deff变大,其原因为热空气流速越高,番木瓜片表面所形成的界面层越薄,番木瓜片与热空气的质热交换越快,同时,热空气流速快可将番木瓜表面所蒸发的水蒸气迅速带走,维持番木瓜表面水蒸汽压与空气中水蒸气压的压差,故有效水分扩散系数增大。

3 结论

通过热风微波耦合干燥单因素实验,得出番木瓜片热风微波耦合干燥阶段主要为降速期,加速期较短,几乎没有恒速期;通过热风微波耦合干燥正交实验,得到番木瓜片热风微波耦合干燥的最佳干燥条件为:热风温度60 ℃、微波功率密度5.5 W·g-1、热风风速0.5 m·s-1;同时,各因素对干燥综合效果影响的主次顺序为:微波功率密度>热风温度>热风风速。

Page模型能较好地预测番木瓜片在热风微波耦合干燥过程中水分比与干燥时间的变化关系,其干燥动力学模型为:MR=exp(-0.0011T-0.0069PD+0.073t(0.0015T2-0.1993T+7.9642));番木瓜片热风微波耦合干燥有效水分扩散系数介于2.533×10-9～6.0792×10-9m2/s之间,且有效水分扩散模型为:10-10Deff=0.507T+6.72PD+10.1v-32。

[1]张海东,胡小婵.世界番木瓜科研发展现状研究[J].世界农业,2013(11):24-27.

[2]Tripathi S,Suzuki J Y,Carr J B,et al. Nutritional composition of Rainbow papaya,the first commercialized transgenic fruit crop[J].Journal of Food Composition and Analysis,2011,24(2):140-147.

[3]Glass transition Phenomenon on shrinkage of papaya during convective drying[J]. Journal of Food Engineering,2012,108(1):43-50.

[4]MASKAN M. Drying,Shrinkage and rehydration characteristics of kiwifruits during hot air and microwave drying[J]. Journal of Food Engineering,2001,48(2):177-182.

[5]Zhang M,Tang J,Mujumdar A S,et al. Trends in microwave related drying of fruits and vegetables[J].Trends in Food Science and Technology,2006,17(10):524-534.

[6]Gowen A,Nissreen A,Frias J M,et al. Characteristics of cooked chickpeas and soybeans during combined microwave-convective hot air drying[J]. Journal of Food Processing and Preservation,2007,31(4):433-453.

[7]陈桂芬,宋春芳,崔政伟.响应面分析法优化热风微波耦合干燥油茶籽工艺[J].食品工业科技,2012,33(3):272-275.

[8]Babalis S J,Papanicolaou E,Kyriakis N,et al. Valuation of thin-layer drying models for describing drying kinetics of figs(Ficus carica)[J]. Journal of Food Engineering,2006,75(2):205-214.

[9]孙帅,崔政伟.柱状胡萝卜样品热风微波耦合干燥数学模型[J].食品工业科技,2013,34(12):161-172.

[10]张斌尧.一种功率连续可调的热风微波耦合干燥系统的研制[D].昆明:昆明理工大学,2016.

[11]GB5009.3-2010食品安全国家标准食品中水分的测定[S].2010.

[12]张丽华,徐怀德,李顺峰,等.不同干燥方法对木瓜干燥特性的影响[J].农业机械学报,2008,39(11):70-75.

[13]周韵,宋春芳,崔政伟,等.热风微波耦合干燥胡萝卜片工艺[J].农业工程学报,2011,27(2):382-386.

[14]陈健凯,林河通,林艺芬,等.基于品质和能耗的杏鲍菇微波真空干燥工艺参数优化[J].农业工程学报,2014,30(3):277-284.

[15]王红提,郭康权,李鹏等. 疏解棉秆的微波干燥动力学及能耗分析[J].农业工程学报,2015,31(19):294-301.

[16]陶菊春,吴建民. 综合加权评分法的综合权重确定新探[J]. 系统工程理论与实践,2001,21(8):43-48.

[17]Corrêa P C,Botelho F M,Oliveira G H H,et al. Mathematical modeling of the drying process of corn ears[J]. Acta Scientiarum Agronomy,2011,33(4):575-581.

[18]Shi Q,Zheng Y and Zhao Y. Mathematical modeling on thin-layer heat pump drying of yacon(Smallanthus sonchifolius)slices[J]. Energy Conversion and Management,2013,71:208-216.

[19]Figiel A. Drying kinetics and quality of beetroots dehydrated by combination of convective and vacuum-microwave methods[J]. Journal of Food Engineering,2010,98(4):461-470.

[20]姜苗.云南核桃热风干燥特性及传质模拟[D].昆明:昆明理工大学,2013.

[21]杨薇,黄小丽,张付杰,等.脉冲电场预处理马铃薯片微波干燥动力学研究[J].昆明理工大学学报(自然科版),2012,37(4):78-84.

[22]Yi X-K,Wu W-F,Zhang Y-Q,et al. Thin-Layer Drying Characteristics and Modeling of Chinese Jujubes[J]. Mathematical Problems in Engineering,2012,2012(4):94-113.

[23]朱文学.食品干燥原理与技术[M].北京:科学出版社,2009.

[24]KL Yeo. Drying of Guava and Papaya:Impact of Different Drying Methods[J].Drying Technology,2006,24(1):77-87.

[25]杨彬彬.多孔介质干燥分形孔道网络模拟及实验研究[D].北京:中国农业大学,2006.

[26]郭徽,杨薇,刘英,等.云南三七主根干燥特性及其功效指标评价[J].农业工程学报,2014,30(17):305-313.

[27]Madamba P S,Driscoll R H,Buckle K A.The thin-layer drying characteristics of garlic slices[J]. Journal of Food Engineering,1996,29(1):75-97.

Drying conditions and drying model of papaya slices during combined microwave-convective hot air dehydration

YI Li,YANG Wei*,WANG Chen

(Faculty of Modern Agricultural Engineering,Kunming University of Science and Technology,Kunming 650500,China)

In order to study the drying characteristics and optimum conditions of combined microwave-convective hot air drying of papaya slices,several test index values,such as colour change,rehydration ratio,drying rate and unit energy consumption during drying process were investigated,and the technological parameters of hot air temperatures,microwave power densities and hot air velocities were optimized. The laboratory-made dryer,having the characteristics of microwave power continuously adjustable and the material heated evenly,was used to do single factor test and orthogonal test for combined microwave-convective hot air drying. Combined microwave-convective hot air drying curve and drying rate curve of papaya slices were obtained for different technological parameters. The drying kinetics model and effective moisture diffusion model of papaya slices during combined microwave-convective hot air drying were established. The results showed that combined microwave-convective hot air drying process of papaya slices consisted of a brief acceleration period and a prolonged deceleration period. Combination drying with hot air temperature of 60 ℃,microwave power density of 0.5 W/g and hot air velocity of 0.5 m/s was optimal in terms of comprehensive drying index. Microwave power density was the most significant experimental factor in orthogonal test of combination drying. Page model was proved to be more suitable in describing combined microwave-convective hot air drying characteristics of papaya slices,and the equation was:MR=exp(-0.0011T-0.0069PD+0.073t(0.0015T2-0.1993T+7.9642)). The effective moisture diffusivity was among 2.533×10-9～6.0792×10-9m2/s,and the effective moisture diffusion model of combination drying of papaya slices was:10-10Deff=0.507T+6.72PD+10.1v-32.

papaya slices;combination drying;drying conditions;drying model

2016-11-17

易丽(1992-)，女，在读硕士，主要从事农产品加工与机械的研究，E-mail:710573682@qq.com。

*通讯作者:杨薇(1963-),女，硕士，副教授，主要从事农产品加工与机械的研究，E-mail:1084406147@qq.com。

TS255.1

B

1002-0306(2017)09-0221-07

10.13386/j.issn1002-0306.2017.09.034