以工作量均衡为目标的成品油配送路径优化问题研究

陈伟峰

[摘 要]文章以成品油配送路径优化问题为背景，研究了以工作量均衡为主要目标的成品油配送路径优化问题（Refined Oil Distribution Route Optimization Problem）。在考虑车辆容载量、加油站允许卸油时间窗、加油站服务时间、加油站需求量等约束的前提下，将各个车辆的工作时间尽可能均衡作为主要目标，建立了以车辆的最大工作时间最小化为目标函数的成品油配送路径优化问题的整数规划模型，编写了求解模型的Lingo程序。文章进一步用随机生成的方式，产生了10个加油站的计算实例，利用Lingo软件求出了局部最优解。通过Lingo软件求得的局部最优解表明了模型的可行性。文章的研究结果为调度部门制订成品油配送计划提供了理论依据。

[关键词]工作量均衡；硬时间窗；库存路径优化；数学模型

[DOI]10.13939/j.cnki.zgsc.2017.15.241

库存和运输是物流系统最重要的功能要素，是物流获得“时间价值”和“空间价值”的两大主要环节，它们的耗费约占物流总成本的2/3。[1]经典的库存路径问题主要研究一个供应商向多个顾客提供配送服务时，在保证顾客的需求量、顾客的配送时间窗以及库存容量限制等约束条件的前提下，使总成本达到最小。对于IRP问题，国内外已经有较多的学者去研究并得出了丰富的理论。Clauclia Archetti[2]等人提出了离散时间下的配送问题，以库存和运输成本最小化作为目标函数。Pieter Vansteenwegen[3]等人研究了单车辆循环库存路径问题，考虑单车辆循环配送问题，不考虑有无限车辆可以使用的情况，是以总成本的最小化作为主要考虑因素。Kunpeng Li[4]等人研究了成品油配送过程中的库存路径问题，在每个加油站只能被服务一次且采用最大补货量原则的前提下，以总运输时间最小化作为主要的目标函数，建立了数学模型并设计了禁忌搜索算法对模型进行求解。李相勇[5]于2007年提出了带时间窗和随机旅行时间车辆路径问题，并设计了基于随机模拟的禁忌搜索算法。蒋波[6]在研究带时间窗车辆路径优化问题时，给出了以配送总成本最小化为目标的带惩罚函数的VRPTW优化模型，并用遗传算法进行了求解。

1 问题描述

本文主要以油库向各个加油站配送成品油作为主要的研究背景。考虑由加油站管理库存的成品油配送物流系统，基于工作量均衡的成品油配送库存路径优化问题可以描述为：一座油库为n个加油站供应某种型号的成品油，假设油库的库存量足够大，已知油库拥有K辆运输车，每辆运输车辆的容载量已知；一辆运输车在油库装满成品油以后，由油库出发依次为若干个加油站配送成品油，配送结束后返回到油库；每个加油站都有一个固定的卸油时间窗，运输车必须在加油站的规定时间窗内为加油站卸油；如果运输车辆早于加油站最早服务时间到达，则运输车必须等待；如果运输车晚于加油站的最晚时间到达，则会造成加油站断货，因此不允许车辆晚于加油站最晚服务时间到达加油站；同一加油站的需求量可以由多辆运输车进行配送；已知每辆运输车的容载量、加油站对成品油的需求量、油库和加油站之间以及各个加油站之间的最短运输距离、每个加油站卸油（服务）所需时间以及加油站的时间窗。如何安排运输车的运输路径及运输量才能使各辆运输车的工作时间尽可能均衡？

2 基于工作量均衡的库存路径优化问题的数学模型

目标函数（1）表示极小化所有车辆完成配送任务的最长时间；

约束（2）表示每个加油站至少被一辆运输车服务；

约束（3）～（4）表示每一辆运输车的运输路径起点和终点都必须是油库；

约束（5）表示一辆运输车进入某个加油站，则必然要从该加油站离开；

约束（6）表示运输车辆所装载的成品油的总量不超过运输车的容载量；

约束（7）表示同一运输路径上相继两个加油站的车辆到达时间之间的关系；

约束（8）表示车辆到达加油站的时间必须在加油站的时间窗内；

约束（9）表示所有车辆运至某一加油站的成品油数量等于其需求量；

约束（10）表示所有车辆回到油库的时间均不超过最长时间；

约束（11）～（12）表示变量的取值约束。

3 算例及求解

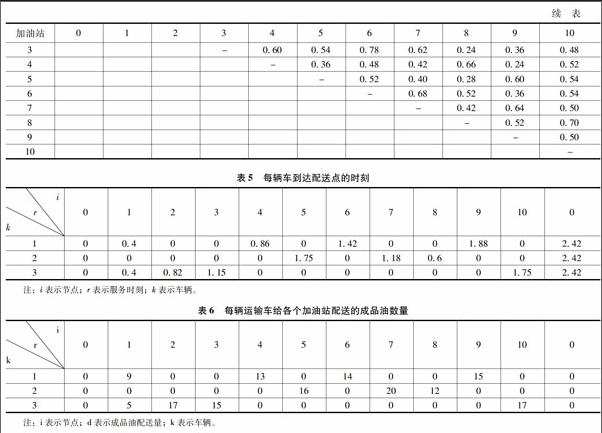
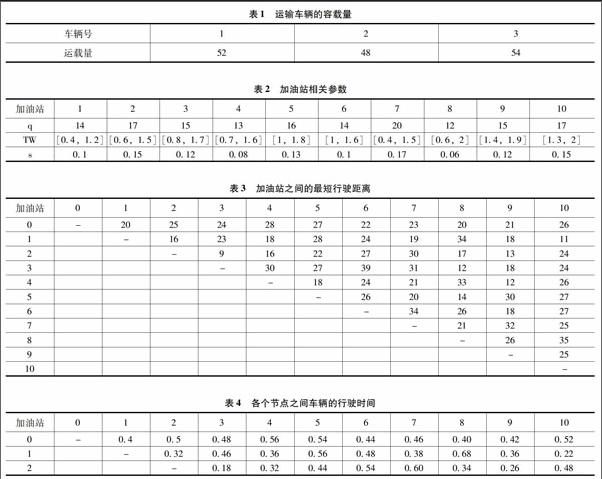
假设有一油库为10个加油站配送成品油，序号0表示油库，序号1～10表示加油站，油库共有3辆运输车，运输车的行驶速度均为50km/h，每辆运输车的容载量不相同。每辆车的容载量见表1，每个加油站的需求量、服务时间及硬时间窗见表2，每个加油站之间以及加油站与油库之间的距离见表3，每个加油站之间以及加油站与油库之间的车辆行驶时间见表4，问如何安排配送路径才能使3辆车的工作时间尽可能均衡？

根据本文建立的整数规划模型，利用Lingo软件编程求解，当求解选项设置为全局最优解时，Lingo经过30个小时的程序运行之后得到全局最优解，具体结果如下所示：

由表5可以得知：车辆1的工作时间为2.42h，车辆2的工作时间为2.42h，车辆3的工作时间为2.42h。

每辆运输车给各个加油站配送的成品油数量如表6所示。

通过Lingo求得局部最优解的用时较长，无法满足短时间内求得最优解的要求。

4 结 论

库存路径优化问题是制订成品油配送计划的关键问题，在实际安排成品油配送方案的时候，经常需要考虑各个配送车辆的工作时间的均衡问题。本文研究的基于工作量均衡的库存路径优化问题的目标就是尽可能使配送车辆的工作时间均衡。本文首先建立了该问题的数学模型，并编写了求解模型的Lingo程序，进一步设计了求解模型的启发式算法。本文的模型和算法为制订成品油配送计划提供了理论依据。

参考文献：

[1]Herer Y.，Levy R..The Metered Inventory Routing Problem，an Integrative Heuristic Algorithm[J].International Journal of Production Economics，1997，51（1）：69-81.

[2]Clauclia Archetti，Nicola Bianchessi，Stefan Irnich，et al.Formulations for an Inventory Routing Problem[J].International Transactions in Operational Research，2014（21）：353-374.

[3]Pieter Vansteenwegen，Manuel Mateo.Aninterated Search Algorithm for the Single-Vehicle Cyclic Inventory Routing Problem[J].Operational Research，2014，237（3）：802-813.

[4]Kunpeng Li，Bin Chen，Appalyer Sirakumar，et al..An inventory-Routing Problem with the Objective of Travel Time Minimization[J].European Journal of Operational Research，2013，236（3）：936-945.

[5]李相勇.车輛路径问题模型及算法研究[D].上海：上海交通大学，2007：91-105.

[6]蒋波.基于遗传算法的带时间窗车辆路径优化问题研究[D].北京：北京交通大学，2010：8-44.