多变量残差修正的灰色模型在建筑物沉降预测中的应用
2017-06-05吕继兵
吕继兵
(湖南省有色地质勘查局二四七队,湖南 长沙 410129)
多变量残差修正的灰色模型在建筑物沉降预测中的应用
吕继兵
(湖南省有色地质勘查局二四七队,湖南 长沙 410129)
多变量灰色MGM(1,n)模型对建筑物的沉降监测将会产生更好的预测结果,但是灰色MGM(1,n)预测模型存在着自身的缺陷,具有系统的误差。基于此,通过对传统MGM(1,n)模型的残差序列进行修正,建立优化的灰色EMGM(1,n)模型。最后,以某建筑物的沉降实测数据为基础,建立灰色GM(1,1)、MGM(1,n)和EMGM(1,n)模型的预测结果并进行比较,结果表明:灰色EMGM(1,n)模型的预测精度优于灰色GM(1,1)和MGM(1,n)模型,新模型使预测结果更加准确、可靠。
多变量灰色模型;残差修正;沉降监测;沉降预测
变形监测可为建筑物的沉降、滑坡与塌陷灾害的预防和治理等工作提供科学的决策依据。在多期监测数据的基础上,如能建立合理的预测模型,不仅可减少监测工作的次数,降低变形监测的成本,而且还能为灾害预防提供判断依据,可把灾害的损害程度降到最小。灰色理论为预测模型的建立提供了有效的理论支持,其在建筑物的沉降监测预测中具有潜在的优势。近年来,国内外学者围绕灰色理论在沉降监测预测方面的应用进行了大量研究。文献[1]对传统的灰色GM(1,1)模型的初值优化、背景值的改正以及残差修正3个方面进行综合优化,进行了大坝沉降监测预测分析,该方法可获得较高精度的大坝沉降预测结果。文献[2]应用3种不同的灰色GM(1,1)模型进行高速铁路隧道围岩短期的沉降,结果表明灰色GM(1,1)预测模型在沉降的短期预测中能够满足隧道围岩沉降监测的需求。文献[3-7]分别从初值的选取、背景值重构以及残差修正方面着手,进行了传统灰色GM(1,1)模型的优化研究。但是,传统的灰色GM(1,1)模型没有充分考虑处于同一沉降体上各沉降点之间的相关信息,不足以反映整个建筑物的沉降规律。同时考虑到处于同一沉降体的各个离散沉降监测点,建立多变量灰色MGM(1,n)模型[8-9]将会产生更好的预测效果。文献[10-11]将多变量灰色MGM(1,n)模型分别应用到路基沉降和滑坡监测工程中,得到了比传统灰色GM(1,1)模型更好的预测结果。但是,传统的灰色MGM(1,n)预测模型仍存在着自身的缺陷,具有系统的误差,因此,本文通过对传统MGM(1,n)模型的残差序列进行修正,建立了优化的灰色EMGM(1,n)模型,同时应用于某高层建筑物沉降监测中,进行预测验证,并与传统的灰色GM(1,1)和MGM(1,n)模型进行比较分析。
1 多变量残差修正的灰色EMGM(1,n)模型
多变量灰色MGM(1,n)模型能够较好地反映系统中各变量之间相互制约、相互影响的关系,且当n=1时,模型退化为灰色GM(1,1)模型。将多变量灰色MGM(1,n)模型的预测序列与原始序列进行比较生成残差序列,再将残差序列进行处理,修正预测序列,使得预测更加准确,残差修正的多变量灰色GM(1,n)模型称为灰色EMGM(1,n)模型。
1.1 多变量灰色MGM(1,n)模型
多变量灰色MGM(1,n)模型的建模步骤参考文献[8-11],如下:假设沉降体上有n个相关联的沉降观测点,实测n个观测点的m周期的沉降观测数据,其相应的沉降观测数据序列记为{Xi(0)}。
(1)
对数据{Xi(0)}序列进行一次累加,生成累加数据序列,记为{Xi(1)}。
(2)
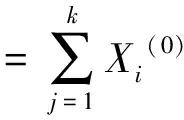
灰色MGM(1,n)模型的白化微分方程组形式为:
(3)
式(3)的矩阵形式为:
(4)

离散化式(4),即可得到式(4)的灰色微分方程[9-10]为
(5)
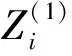
利用最小二乘原理求取模型中的参数A和B的估值得:
(6)
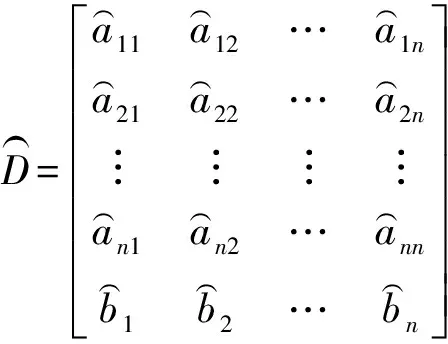
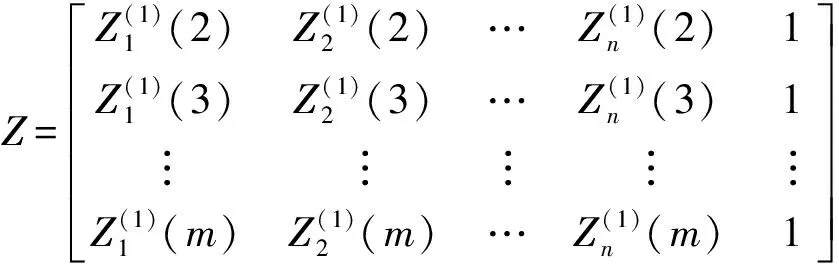
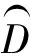
式(3)的时间响应方程式(预测方程)为:
(7)

最后,恢复时间序列,还原得到预测值为:
(8)
1.2 基于残差修正的灰色MGM(1,n)模型
传统的多变量灰色MGM(1,n)模型本身存在模型的系统误差,假设对生成的预测残差序列进行进一步处理,将会对模型预测起到修正作用。这里,为了提高预测精度,参照文献[12],将多变量灰色MGM(1,n)模型的残差序列进行处理并修正预测序列,其具体步骤如下:

(9)
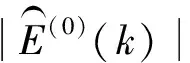
3)赋予绝对值残差序列的预测序列正确的符号,与原始残差序列符号相同,即
(10)
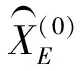
(11)
2 工程应用
2.1 工程概况
该工程为长沙市某项目的市政工程新建的居民楼,在居民楼1#~8#楼布设28个沉降观测点,按照二等水准测量的要求进行往返测量,每次施测时对监测点进行累计沉降记录,以确定每栋楼沉降的稳定性。文中以第6#楼为例,由工作基点K6开始对6#楼的沉降点按照二等水准测量的要求进行往返测量, 选取位于6#楼的A,B,C3个监测点的12期累计沉降量数据作为本次实验数据,其中前8期数据用于建模,后4期数据用于检验和比较预测值的准确性,原始的累计沉降观测数据如表1所示。
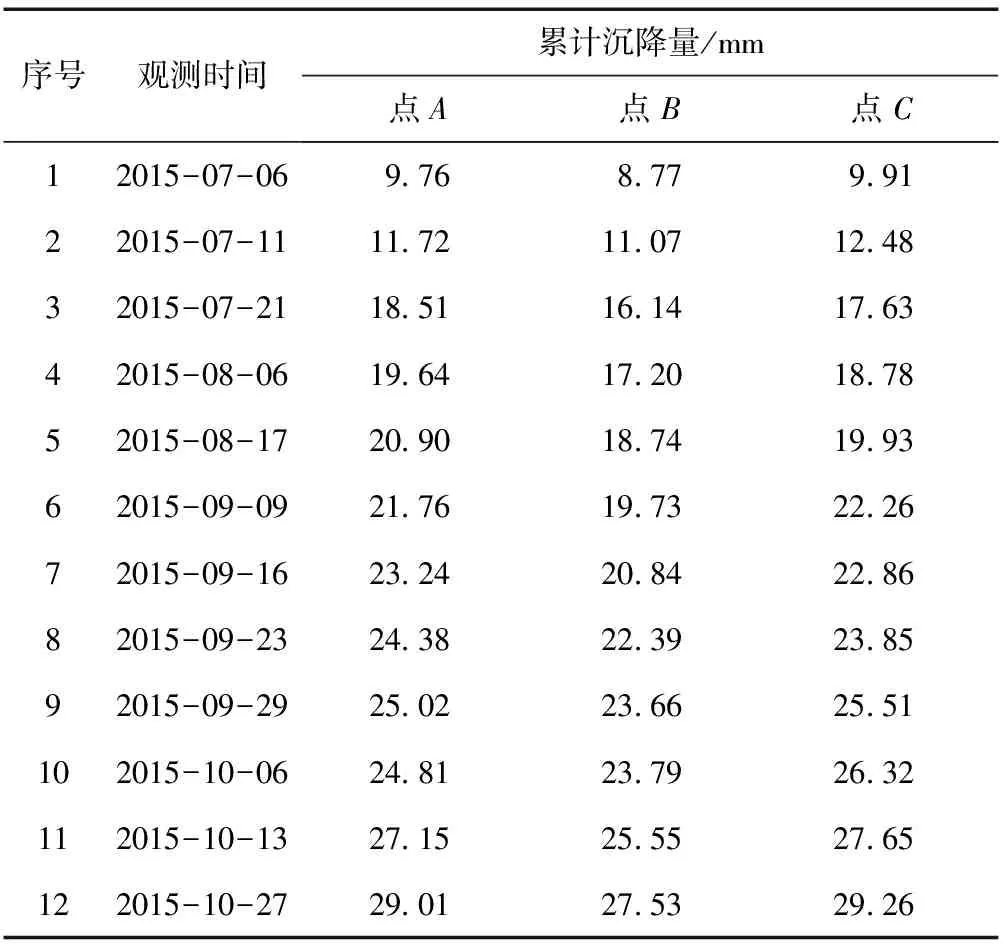
表1 实测沉降累计数据
2.2 数据结果分析
利用MATLAB R2013为实验平台,参考文献[1-6],依据监测点A,B,C的前8期实测数据,分别建立传统的灰色GM(1,1)模型并进行后4期数据的预测;按照文中灰色MGM(1,3)模型的建模过程,分别建立A,B,C3个监测点的多变量灰色预测模型;按照残差修正理论建立残差修正的多变量灰色EMGM(1,3)模型,预测计算3个监测点的第9~12期的预测值。A,B,C3个监测点的3种模型的预测结果如表2~表4所示。
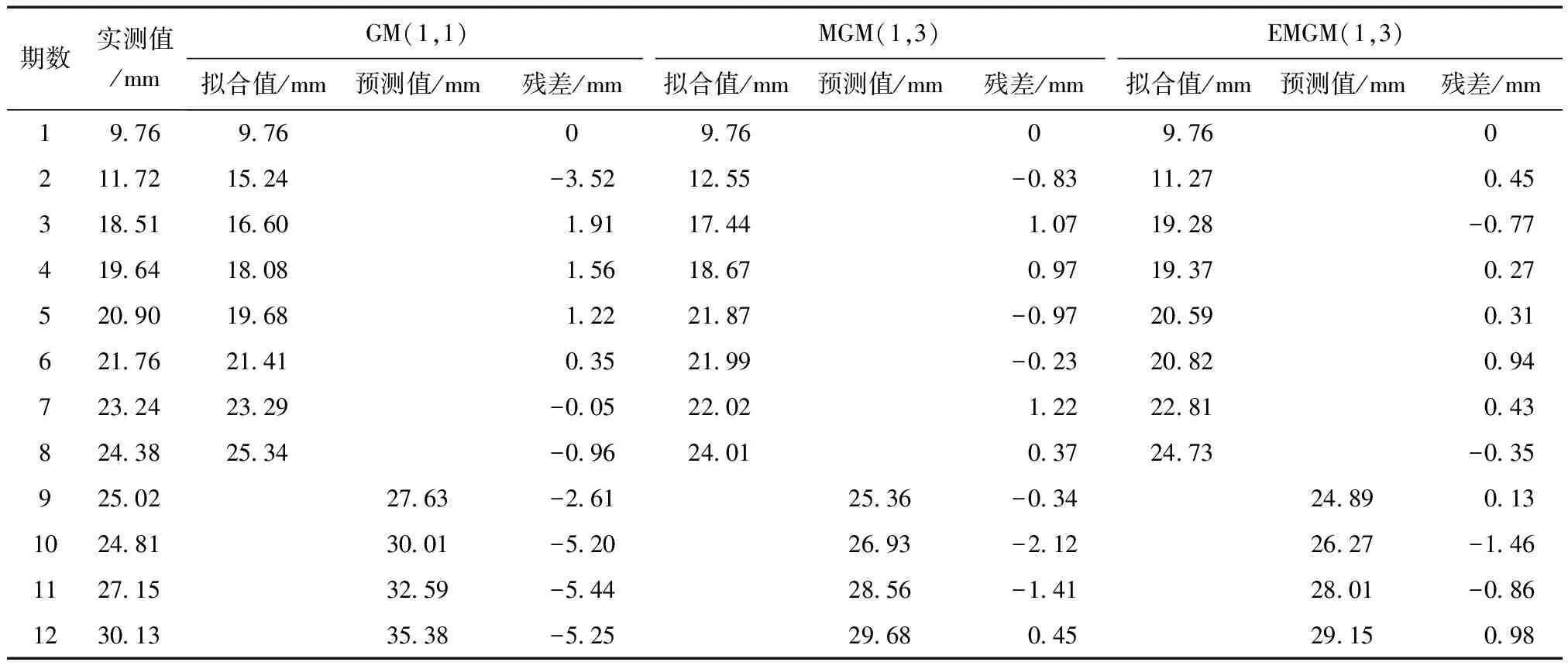
表2 监测点A 3种模型拟合值和预测值

表3 监测点B 3种模型拟合值和预测值

表4 监测点C 3种模型拟合值和预测值
另外,以监测点B为例,3种预测模型的预测数据与实测数据曲线比较如图1所示。
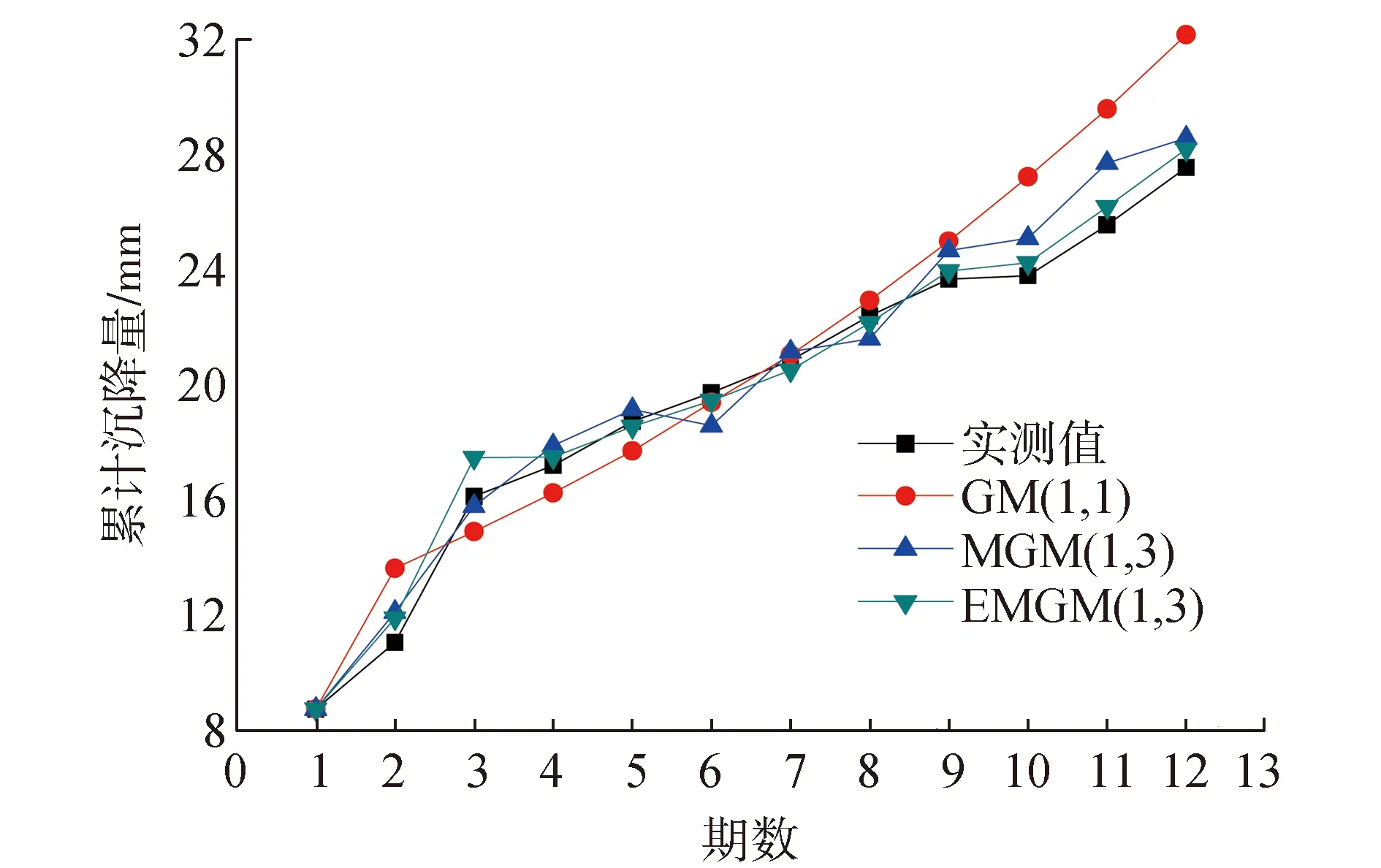
图1 监测点B的预测值与实测值比较
从表2可以看出,沉降监测点A的灰色EMGM(1,3)模型的预测值残差中误差为1.13 mm,灰色MGM(1,3)模型的预测值残差中误差为1.51 mm,传统的灰色GM(1,1)模型的预测值残差中误差为5.50 mm;从表3可以看出,沉降监测点B的灰色EMGM(1,3)模型的预测值残差中误差为0.60 mm,灰色MGM(1,3)模型的预测值残差中误差为1.66 mm,传统的灰色GM(1,1)模型的预测值残差中误差为4.11 mm;从表4可以看出,沉降监测点C的灰色EMGM(1,3)模型的预测值残差中误差为0.64 mm,灰色MGM(1,3)模型的预测值残差中误差为1.77 mm,传统的灰色GM(1,1)模型的预测值残差中误差为4.46 mm;从计算出来的预测值中误差,3个监测点的残差修正的多变量灰色EMGM(1,3)模型的预测值残差中误差均小于传统的多变量灰色MGM(1,3)模型的预测值残差中误差和传统的灰色GM(1,1)模型;同时,从图1可以看出,以沉降监测点B为例的原始观测值与预测值的曲线拟合效果最好。从3个监测点的预测值可以看出,残差修正的多变量灰色EMGM(1,3)模型的预测值更具参考价值。
3 结束语
针对传统的灰色MGM(1,n)预测模型存在着自身的缺陷,具有系统的误差,本文通过对传统MGM(1,n)模型的残差序列进行修正,建立优化的灰色EMGM(1,n)模型,并应用于某建筑物沉降监测中,进行预测验证并与传统的灰色GM(1,1)和MGM(1,n)模型的预测结果进行比较分析,得出的结论为:多变量残差修正的灰色EMGM(1,n)模型的预测结果的精度都要优于传统的灰色GM(1,1)和MGM(1,n)模型的结果,有效地克服了以往预测模型中信息不关联的缺陷,灰色EMGM(1,n)模型使预测结果更加准确、可靠,具有实际的参考价值。
[1] 李克昭,李志伟,孟福军,等.基于综合优化GM(1,1)的形变预测模型[J].大地测量与地球动力学,2016,36(2):120-123.
[2] GUO Youlin, ZHAO Minghua, DENG Zongwei. Tunnel Surrounding Rock Settlement Forecast Analysis Based on GM and FEM[J]. Electronic Journal of Geotechnical Engineering, 2014, 19 G:1379-1394.
[3] 张彬,西桂权.基于背景值和边值修正的GM(1,1)模型优化[J].系统工程理论与实践,2013,33(3):682-688.
[4] 李志伟,李克昭,赵磊杰.优化的灰色非等距GM(1,1)预测模型在沉降监测中的应用[J].河南城建学院学报,2016,25(2):68-73.
[5] 袁德宝,崔希民,高宁.同时利用x(1)(1)和x(1)(n)为GM(1,1)建模初始条件的预测方法研究[J].大地测量与地球动力学, 2013, 33(3):79-82.
[6] 郭兰兰,邹志红,安岩.基于残差修正的GM(1,1)模型在水质预测中的应用[J].数学的实践与认识,2014,44(19):176-181.
[7] 李亚磊,林楠.优化的非等距GM(1,1)模型在高层建筑物沉降监测中的应用[J].黑龙江工程学院学报,2016,30(2):8-11.
[8] 崔立志,刘思峰,吴正朋.基于向量连分式理论的MGM(1,n)模型[J].系统工程,2008,26(10):47-51.
[9] 王正新.灰色多变量GM(1,N)幂模型及其应用[J].系统工程理论与实践,2014,34(9):2357-2363.
[10] 李世贵,易庆林,吴娟娟,等.背景值优化的多点灰色模型在滑坡沉降预测中的应用[J].中国地质灾害与防治学报,2015,26(2):3-8.
[11] 刘寒冰,向一鸣,阮有兴.背景值优化的多变量灰色模型在路基沉降预测中的应用[J].岩土力学,2013,34(1):173-181.
[12] 李克昭,李志伟,赵磊杰.马尔科夫理论的优化灰色模型预测建模[J].测绘科学,2016,41(8):1-5.
[责任编辑:郝丽英]
本 刊 声 明
为适应我国信息化建设,扩大本刊及作者知识信息交流渠道,本刊已成为北京万方数据股份有限公司、万方数据电子出版社、中国学术期刊(光盘版)电子杂志社、重庆维普资讯有限公司中文科技期刊等数据库全文收录期刊。来稿一经录用,均视为作者已将该作品全文的数字化方式复制权、发行权、汇编权、翻译权以及信息网络传播权授予本刊编辑部。编辑部已将作者著作权使用费与本刊稿酬一次性结清。作者向本刊提交文章发表的行为即视为接受我刊上述声明的条款。如作者不同意将文章编入该数据库,请在来函中声明,本刊将做适当处理。
Application of a multivariable grey model to settlement prediction of buildings based on residual error
LU Jibing
(No.247 Team, Hunan Bureau of Nonferrous Metal Geological Exploration, Changsha 410129, China)
The multivariable grey MGM(1,n) model will produce better prediction results for settlement monitoring of buildings. But there are defects for the grey MGM(1,n) forecasting model, including the systematic errors. Based on the modification of the residual sequence of the traditional model MGM(1,n), the optimized EMGM(1,n) model is proposed in this paper. At last, this paper effectively compares the grey GM(1,1) model, MGM(1,n) model and EMGM(1,n) model, based on practical data of some building. The result shows that the forecasting accuracy of grey EMGM(1,n) model is better than grey GM(1,1) model’s and MGM(1,n) model’s, and the new model can make the prediction more reliable and accurate, which has practical reference value.
multivariable grey model; residual error; settlement monitoring; settlement prediction
10.19352/j.cnki.issn1671-4679.2017.02.004
2016-10-10
国家自然科学基金资助项目(41202245)
吕继兵(1983-),男,工程师,硕士研究生,研究方向:精密工程测量.
P208
A
1671-4679(2017)02-0016-05
