基于SARIMA模型的船舶交通流量预测研究*

李晓磊 肖进丽 刘明俊

(武汉理工大学航运学院1) 武汉 430063) (湖北省内河航运技术重点实验室2) 武汉 430063)

基于SARIMA模型的船舶交通流量预测研究*

李晓磊1，2)肖进丽1,2)刘明俊1,2)

(武汉理工大学航运学院1)武汉 430063) (湖北省内河航运技术重点实验室2)武汉 430063)

为提高船舶月交通流量预测精度，更合理地为港口规划和发展提供决策依据，选用季节性差分自回归滑动平均(seasonal autoregressive integrated moving average,SARIMA)模型对船舶月交通流量建立了预测模型，并利用Eviews软件，以2007年1月-2015年12月荆州港船舶交通流月均流量统计数据为样本进行了实证分析.对船舶月交通流量时间序列样本数据进行平稳化预处理，消除其趋势成分和季节因素；基于平稳化后的数据建立了SARIMA模型并对模型进行参数检验及最优模型选取；并利用所获得的最优模型SARIMA(2,0,0)(1,1,1)12对2008年1月-2016年3月荆州港船舶交通流月均流量进行预测，并将预测结果与AR(1)模型、季节指数模型的预测结果进行对比分析.对比分析结果表明，SARIMA的预测精度更高，更能反映船舶月交通流量的变化情况，利用该模型对船舶月交通流量进行建模预测具有较好的实用性.

船舶交通流；时间序列；SARIMA模型；预测

0 引 言

船舶交通流量的预测主要有年交通流量预测和月交通流量预测两种.对于月交通流量预测，受气候条件、通航水位等因素的影响，船舶交通流量量统计会存在一定的周期性和季节性特征.目前交通流量预测方法主要有神经网络法、时间序列预测法、支持向量机预测法、组合预测法等[1-5]，许多文献也基于上述方法对船舶年交通流量和月交通流量进行了预测[6-8]，但大多数有关船舶月交通流量预测的研究未考虑季节性影响，从而导致预测结果误差较大.SARIMA模型是一种改进的差分自回归滑动平均(autoregressive integrated moving average model，ARIMA)模型，对于周期性或季节性的时间序列具有较高的预测精度，因此，文中基于SARIMA模型，选取实例通过EVIEWS软件进行月度船舶交通流量统计数据的模型识别、检测及参数选取[9]，完成船舶月交通流量预测与分析.

1 ARIMA模型

SARIMA模型是随机季节模型与ARIMA 模型的组合[10].如果时间序列具有平稳性，则可直接建立ARMA(p，q)模型，但对于具有某种趋势的非平稳时间序列，就需先对其进行平稳化处理.若采用差分方法对非平稳时间序列进行平稳化处理[11]，则一个d阶单整时间序列ARIMA(p,d,q)模型可建立为

(1)式中：Ø(B)=1-ØB-Ø2B2-…-ØpBp是自回归算子；p为自回归阶数；θ(B)=1-θ1B-θ2B2-…-θqBq为移动平均算子；q为移动平均阶数；d为非平稳时间序列成为平稳时间序列所需做的差分次数.

对于非平稳时间序列进行平稳化处理，要判断时间序列的趋势是否消除，可观察经过d阶差分处理后序列的自相关分析图中自相关系数是否快速趋于零.

2 SARIMA模型

SARIMA模型对具有季节性波动的时间序列有较高的预测精度.SARIMA模型又称ARIMA(p,d,q)(P,D,Q)S模型，其一般形式

式中：S为季节性周期长度；φP(Bs)和ΘQ(Bs)分别为季节P阶自回归算子和Q阶移动平均算子；P为季节性自回归阶数；Q为季节性移动平均阶数，D为季节性差分阶数.当P=Q=D=0时，SARIMA模型变为非季节性ARIMA模型.

SARIMA模型具体建模过程如下[13].

1) 序列平稳性预处理 通过时序图和序列相关图判断序列是否具有趋势性和周期性，进一步确定是否需进行逐期差分和季节性差分，从而确定d和D的值，最后用ADF或pp检验逐期差分和季节性差分处理后的序列是否已经平稳.

2) 模型初步定阶 依据逐期差分和季节性差分处理后平稳序列的自相关函数和偏自相关系数特点，以及其出现周期性滞后显著不为0的位置选择合适的p，q，P，Q.

3) 最优模型选择 通过AIC准则、SC准则对p，q，P和Q的可能取值进行比选,最后确定最优SARIMA模型的p，q，P和Q的取值.

4) 模型诊断与检验 根据序列t检验或残差的Q-统计量的值判断残差序列是否为白噪声序列，从而确定模型的合理性.

5) 预测 利用确定的最优SARIMA模型对时间序列进行预测.

3 实例分析

为验证SARIMA模型在船舶交通流量预测中的有效性，选取2007年1月—2015年12月荆州长江公路大桥断面船舶流月均流量统计数据为样本建立SARIMA模型，并基于Eviews对2008年1月—2016年3月船舶交通流月均流量进行预测，并与ARIMA模型、季节指数平滑模型的预测结果以及实际值进行对比分析.

3.1 样本时间序列平稳性预处理

对选取的样本数据绘制时序图(见图1)，由图1可见，该时间序列并未有持续上升或下降的趋势，但含有某种周期性.根据ADF检验(见图2)，t统计值小于显著性水平为1%的临界值，拒绝存在单位根的原假设，表明序列是平稳的，不需要进行逐期差分处理.

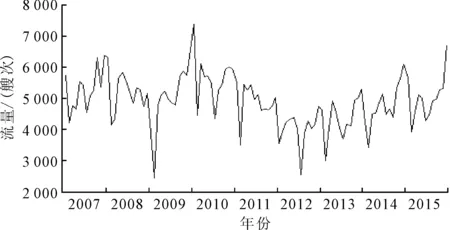
图1 样本时间序列图

图2 时间序列ADF检验图

对选取的样本序列做自相关图和偏自相关分析，观察获得的自相关和偏自相关分析图(见图3)，可见自相关系数和偏相关系数在12阶、24阶等位置出现最大峰值，表明序列有周期为12个月的波动.对序列进行1阶季节差分并做相关性分析，见图4.

图3 序列自相关图和偏自相关图

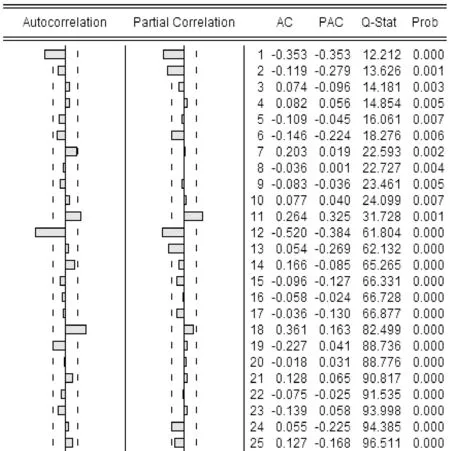
图4 序列1阶季节差分后的自相关和偏相关图

根据图4中序列1阶季节差分自相关和偏自相关系数特点，PAC(partial correlation)函数在二阶截尾，AC(autocorrelation)函数呈现快速衰减且在一阶截尾，但样本的自相关系数和偏相关系数仍滞后12期周期性的显著不为0，可知季节性依然存在.经试验，对序列进行2阶季节差分后发现季节性并没有显著改善，故只做1阶季节差分即可.

通过对序列1阶季节差分的ADF检验(见图5)，t统计值小于显著性水平为1%的临界值，拒绝存在单位根的原假设，表明序列仍平稳，可进行SARIMA建模.

图5 序列1阶季节差分ADF检验图

3.2 SARIMA模型定阶与检验

由于样本时间序列不需进行逐期差分处理，故d取值为0，而样本序列进行了1阶季节差分后季节性基本消除，故D取值也为1.同时，由样本序列的自相关图和偏自相关图，可供选择的(p,q)组合有(1,1)，(2,0)，(2,1)和(3,0).此外，由于样本序列进行季节差分后，序列的自相关和偏自相关系数周期性滞后12期，且在12期时显著不等于0，则P=Q=1.

据此，选择不同(p，q)组合，建立SARIMA(1,0,1)(1,1,1)12，SARIMA(2,0,0)(1,1,1)12，SARIMA(2,0,1)(1,1,1)12及SARIMA(3,0,0)(1,1,1)12四种SARIMA模型并对2008年1月-2016年3月数据进行试预测,其相关检验结果见表1.

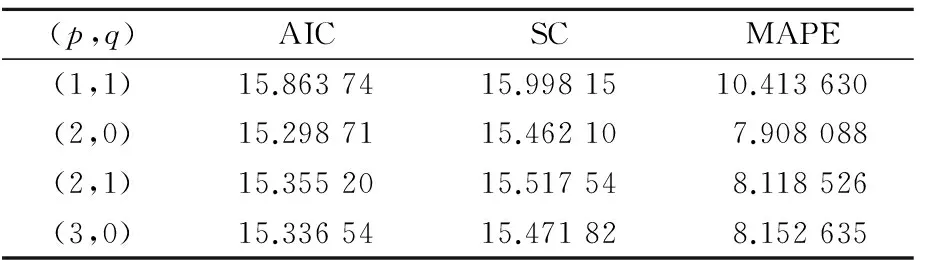
表1 四种SARIMA模型相关检验结果

由表1可知，(p，q)组合为(2，0)时所构建的SARIMA(2,0,0)(1,1,1)12模型的AIC值、SC值以及试预测的平均绝对百分误差(MAPE)都是最小；此外，通过对该模型残差序列进行白噪声检验(见图6)，ACF和PACF都没有显著异于零，Q统计量的P值都远远大于0.05，故残差序列可认为白噪声序列，表明该模型提取的序列信息比较充分，选择SARIMA(2,0,0)(1,1,1)12模型为预测模型是合理的.

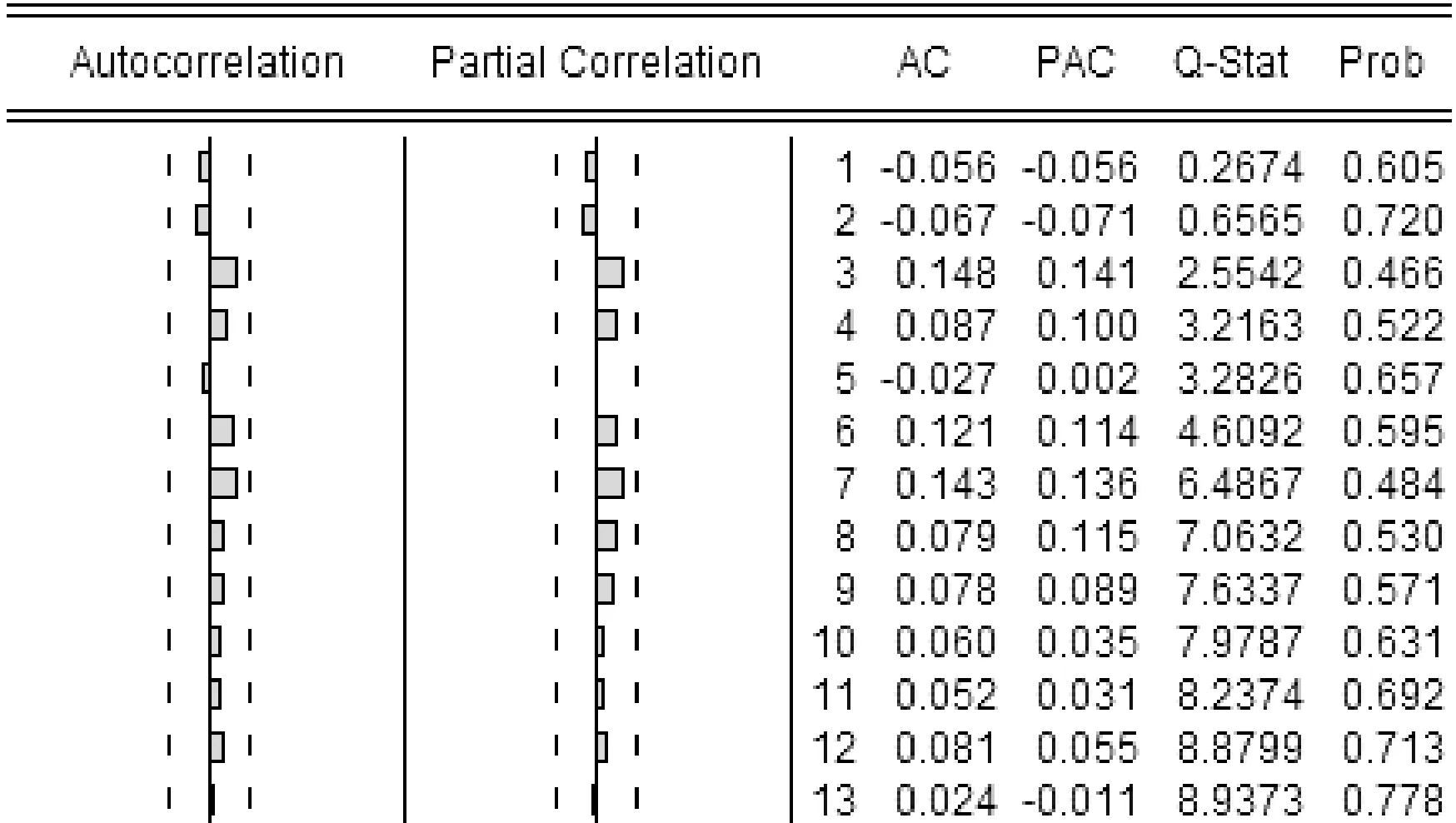
图6 残差白噪声检验图

3.3 ARIMA模型与季节指数模型建模

1) ARIMA模型建模 根据样本序列自相关和偏相关图(见图3)，可看到样本序列的自相关函数拖尾且偏相关函数一阶截尾，符合AR(1)模型的特点，且考虑到AR(1)模型是线性方程估计，相对于ARIMA模型的非线性估计容易，故实际建模时用AR(1)模型替换掉相对应的ARIMA(1,0,0)模型，与SARIMA(2,0,0)(1,1,1)12进行对比.AR(1)模型的t检验结果见图7，此模型的回归系数通过了显著性t检验，且绝对误差较小，AR特征根绝对值小于1，表明该模型基本稳定，拟合准确度也在可接受的范围内.

图7 非季节性AR模型的检验结果图

2) 季节指数模型建模 季节指数平滑模型有Holt-Winters乘法模型和 Holt-Winters 加法模型两种，利用这两种模型对原样本时间序列进行建模预测，其模型检验结果见表2.

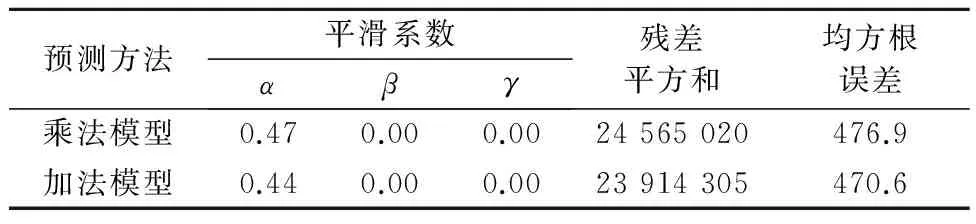
表2 季节指数平滑模型相关检验结果

由表2可知，Holt-Winters 加法模型预测结果的均方根误差和残差平方和均较小，故本文选择拟合较好的Holt-Winters 加法模型与SARIMA模型进行船舶交通流预测比较.

3.4 预测结果与对比分析

根据建立的SARIMA(2,0,0)(1,1,1)12模型、AR(1)模型和Holt-Winters 加法模型对船舶交通流量数据进行预测对比分析，图8～9分别为SARIMA(2,0,0)(1,1,1)12模型与AR(1)模型和Holt-Winters 加法模型交通流量预测对比，表3则为这3种模型于2016年1—3月期间的预测结果与此期间真实数据的比较结果.

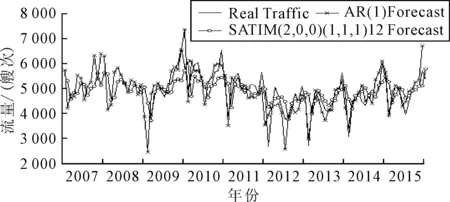
图8 SARIMA(2,0,0)(1,1,1)12和 AR(1) 模型预测对比图

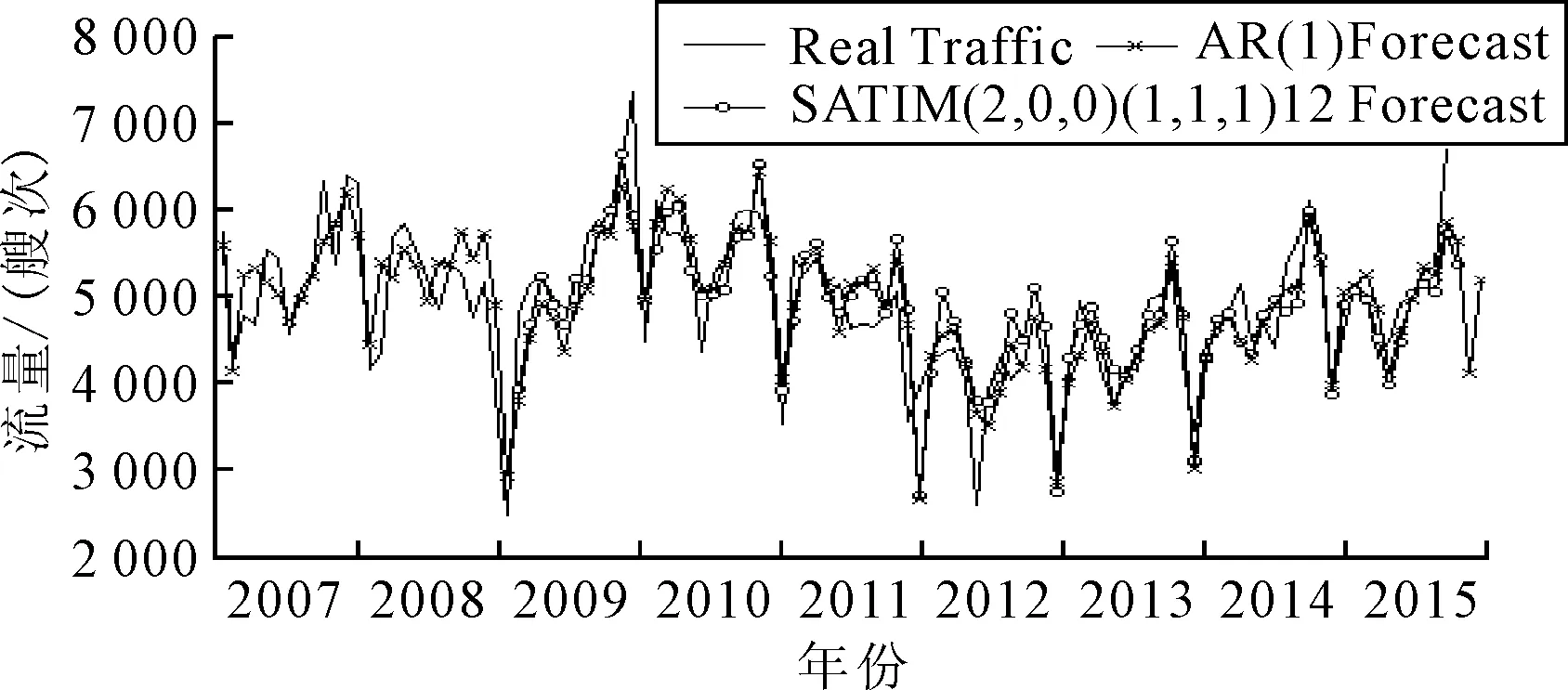
图9 SARIMA(2,0,0)(1,1,1)12和 Holt-Winters加法模型预测对比图

模型时间预测值/(艘次)实际值/(艘次)误差/(艘次)相对误差/%AR(1)2016-0156775739-62-1.02016-025260392713334.02016-0342155703-148-26.0加法模型2016-0156215739-118-2.02016-0240813927154 3.92016-0351735703-5309.3SARIMA(2,0,0)(1,1,1)122016-0153985739-341-5.92016-0239923927651.62016-0353365703-367-6.4

从表3可知，AR(1)模型和Holt-Winters 加法模型预测的相对误差较大，而SARIMA(2,0,0)(1,1,1)12模型预测的相对误差控制在7%内，较AR(1)模型和Holt-Winters 加法模型有更高的准确度且预测结果更贴合实际，拟合度较好，适用性更强.

4 结 束 语

文中给出了利用SARIMA模型对船舶月交通流量进行预测的方法,并与ARIMA模型和Holt-Winters 加法模型进行了实证对比分析.对比分析结果表明，SARIMA模型能够有效地将船舶月交通流量的季节相关性表达出来，比ARIMA模型和季节指数平滑模型的预测精度更高，更能反映船舶月交通流量的变化情况，因此利用该模型对船舶月交通流量进行建模预测具有较好的实用性.但是，由于该模型的建模过程完全依赖于数据本身，不考虑外界影响因子，是一种完全数据驱动的方法，因此具有一定的局限性，需进一步深入研究.

[1]梁德阳.基于SARIMA和BP神经网络的时间序列组合预测模型研究[D].兰州：兰州大学,2014.

[2]毛玉凤.基于时间序列分析的电力需求预测及季节调整模型的研究[D].北京：北京工业大学,2013.

[3]XIAO X P, ZHENG R J. Multi-level recursive method of short-term traffic flow forecast based on PGAGOGM(1,1) model[J]. Management Science and Engineering,2011,53:55-58.

[4]魏杏.基于指数平滑法和ARIMA的交通量组合预测模型应用研究[D].郑州：郑州大学,2014.

[5]CONG Y L, WANG J W, LI X L. Traffic flow forecasting by a least squares support vector machine with a fruit fly optimization algorithm[J]. Procedia Engineering,2016,137：157-162.

[6]黄智仟.基于神经网络的船舶交通流量预测研究[D].大连：大连海事大学,2015.

[7]薛洁,史忠科.基于混沌时间序列分析法的短时交通流预测研究[J].交通运输系统工程与信息,2008,8(5):69-72.

[8]YIN Y, SHANG P J. Forecasting traffic time series with multivariate predicting method[J].Applied Mathematics and Computation,2016(1):5-11.

[9]罗媛媛.基于EVIEWS的短时交通流分析及预测[D].成都：西南交通大学,2009.

[10]黄毅.SARIMA模型在月平均温度时间序列中的应用[D].北京：北京邮电大学,2012.

[11]郝勇,朱海燕.基于客流n日均量的地铁客流量的时间序列分析[J].铁道运输与经济,2009(10):42-50.

[12]张辉,刘嘉琨,柳湘月,等.交通流的季节ARIMA模型与预报[J].天津大学学报,2005,38(9):838-841.

[13]王莹,韩宝明,张琦,等.基于SARIMA模型的北京地铁进站客流量预测[J].交通运输系统工程与信息,2015,15(6):205-210.

Vessel Traffic Flow Prediction Based on the SARIMA Model

LI Xiaolei1,2)XIAO Jinli1,2)LIU Mingjun1,2)

(SchoolofNavigation,WuhanUniversityofTechnology,Wuhan430063,China)1)(HubeiKeyLaboratoryofInlandShippingTechnology,Wuhan430063,China)2)

To improve the predictive accuracy of vessel traffic flow and provide more reasonable decision-making basis for port planning and development, Seasonal Autoregressive Integrated Moving Average (SARIMA) model is put forward to predict the monthly traffic flow of vessel. Based on the software Eviewsis, empirical analysis is carried out for the vessel traffic flow monthly statistical data of Jingzhou port during January 2007-December 2015. Firstly, the sample data from the vessel traffic flow monthly statistics of Jingzhou port is executed stationary pre-process, in order to eliminate the trend component and seasonal factors of the statistical data. Afterwards, the SARIMA model based on the data through stationary pre-treatment is set up. Then the model parameters are test and the optimal model SARIMA(2,0,0) (1,1,1)12is validated. Finally, the prediction of the vessel traffic flow during January 2008-March 2016 of Jingzhou port is made, and the prediction results are compared with the those using AR (1) model and seasonal exponential model. The comparison results show that the SARIMA prediction accuracy is higher, and can reflect the monthly change characteristics of vessel traffic flow more accurately.

vessel traffic flow; time series; SARIMA model; prediction

2017-01-13

*湖北省自然科学基金面上项目资助(2015CFB282)

U491.14

10.3963/j.issn.2095-3844.2017.02.030

李晓磊(1993—)：男,硕士生,主要研究领域为交通信息处理及交通安全保障技术