体积力法在船舶自由直航数值计算中的影响因素研究*

吴 浩 欧勇鹏 向 国

(海军工程大学舰船工程系 武汉 430033)

体积力法在船舶自由直航数值计算中的影响因素研究*

吴 浩 欧勇鹏 向 国

(海军工程大学舰船工程系 武汉 430033)

为了探索体积力法在船模自由直航数值计算中的适用性及影响因素，针对某双尾鳍船型，采用体积力法建立虚拟桨模型，探讨了进流盘面的半径、偏移量等对航速的影响规律，并与自航模试验结果进行对比.结果表明，进流盘半径对航速的影响较大，而偏移量对航速影响较小；采用体积力法建立虚拟桨模拟船模自由直航，航速计算精度可达0.5%，最大偏差不超过5%.

数值计算；自由直航；体积力法；自航模

0 引 言

通过体积力法构建虚拟螺旋桨，忽略不必要的流动细节，可大幅节约计算网格，提高计算效率，可用于开展船模操纵运动的数值模拟.Pablo等[1]基于体积力法模拟了水面舰艇MARIN-7967的回转及Z形试验，Ryan等[2]结合重叠网格计算对水下航行器的Z形运动模拟进行了研究.Alexander等[3]则采用blade element momentum theory方法计算了全附体KVLCC2的直航运动及自航点，所得结果的误差为3%左右.但值得注意的是，上述学者并未公开虚拟桨的影响因素及相关设置.

为此，本文基于RANS方程结合六自由度模型，研究进流盘面的半径、偏移量等对航速的影响规律，并通过与自航模试验结果进行对比，探索进流盘面的半径、偏移量的优化方案，以期为船舶自由自航的数值模拟研究提供支撑.

1 数值计算方法

1.1 控制方程

不可压缩流体雷诺平均的连续性方程和动量方程为

(1)

(2)

由于2个方程不封闭，所以需要湍流模型对雷诺应力项进行处理，选用k-ε模型，控制方程如下.

(3)

(4)

1.2 体积力法

体积力法将推力按半径变化分布在由桨盘面直径、螺旋桨纵向厚度所定义的圆柱区域内，建立虚拟螺旋桨.而虚拟螺旋桨的推力、转矩则根据桨前方进流盘的平均速度，在敞水性能曲线上插值而得.其中，进流盘及其半径r′与偏移量ΔL的定义见图1.

图1 进流盘半径及偏移量

虚拟桨上轴向力与切向力的分布采用Goldstein优化方式，数学表达式如下.

(5)

(6)

其中：fbx为轴向力；fbθ为切向力；RP为螺旋桨半径；RH为桨毂半径；r为辐射半径；T，Q分别为敞水螺旋桨的推力和转矩.

螺旋桨的敞水性能曲线见图2，采用六次多项式进行拟合，多项式系数见表1.

图2 螺旋桨敞水性能曲线

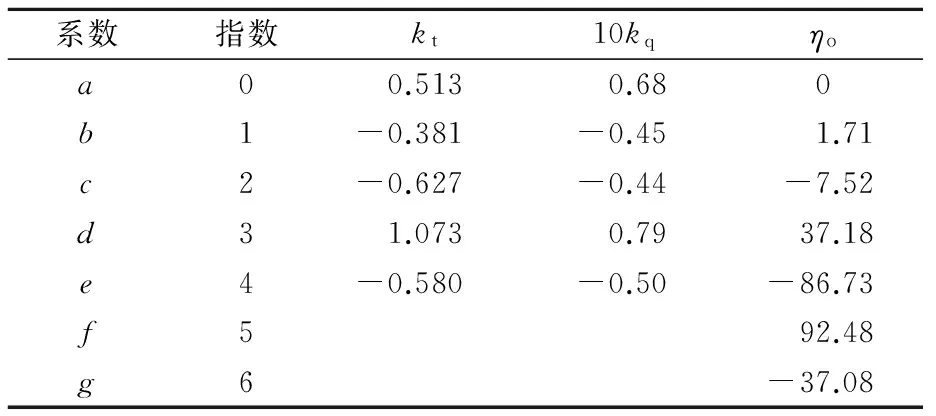
系数指数kt10kqηoa00.5130.680b1-0.381-0.451.71c2-0.627-0.44-7.52d31.0730.7937.18e4-0.580-0.50-86.73f592.48g6-37.08

1.3 计算对象及流域网格

计算所用船模见图3，模型长L=5 m，吃水T=0.18 m，排水量Δ=340 kg，重心纵向位置为xG=-1.30%L，螺旋桨直径为0.13 m，纵向厚度0.026 m.

图3 计算对象三维侧视图

图4给出了计算模型的流域和网格设置.计算域采用全六面体剪切型网格，在船体、舵、桨、自由液面等区域进行了网格加密.边界层网格厚度为0.24%

L

，设置为6层，厚度的增长率为1.2，网格总数为150万.虚拟桨及船尾网格见图5.

图4 计算流域

图5 船尾及桨盘面网格

2 计算结果分析

计算在Star CCM+软件平台上实现，基于RANS方程，同时采用了VOF两相流模型、刚体六自由度运动模型、区域动网格模型.计算过程中，虚拟桨直径为130 mm，沿流动方向的厚度为26.4 mm，转速n=820 r/min，所得结果及分析如下.

2.1 进流盘面半径的影响

表2给出了进流盘半径r′的变化范围，表中RP表示螺旋桨半径.此时，进流盘面的偏移量ΔL=0.1RP.

表2 进流盘半径变化范围

图6给出了模型航速和虚拟桨推力随进流盘半径的变化.由图6可知，进流盘半径对航速与推力有较大影响，当r′/Rp<0.8时，随着进流动盘半径的增加，速度与推力值迅速降低；当r′/Rp>0.8时，速度与推力变化不大，基本趋于一个稳定值.

当r′/Rp=0.59时，所得航速值为Vm=1.38 m/s，与试验结果相一致.可见，当进流盘的偏移量ΔL/RP=0.1时，其半径可取为r′/Rp=0.59.

图6 进流盘半径对速度与推力的影响

2.2 进流盘面偏移量的影响

表4给出了进流盘偏移量的变化范围，其中进流盘的半径r′/Rp=0.5.

表4 进流盘偏移量变化范围

进流盘偏移量对航速和推力的影响见图7.由图7可知，航速和推力随着进流盘偏移量的增加而增大，但变化不大，且几乎呈线性关系，即

图7 进流盘偏移量对速度与推力的影响

(9)

式中：Vm为速度的变化量；ΔL/Rp为偏移量的变化.可见，线性关系式的斜率为0.001 8，说明航速随偏移量的变化不大；无因次偏移量每增大5%，速度增加0.01 m/s.

2.3 影响参数的选取方法与验证

由2.1节与2.2节的研究可知，采用体积力法构建虚拟螺旋桨，计算船舶自由直航时，虚拟桨进流盘的半径是主要影响因素，而进流盘偏移量对计算结果有所影响，但影响不大.为此，在选择进流盘参数时，可采用如下方法：

1) 系列改变进流盘直径，且其变化范围为0.5

2) 保持进流盘半径不变，根据目标航速及式(9)，确定进流盘偏移量的修正值，直至计算所得自由直航的航速与目标值基本一致.

根据上述方法，分别计算了螺旋桨转速n=300～1 100 r/min下的自由直航，并与试验结果进行对比，见图8.

图8 体积力法计算所得航速随转速的变化

由图8可知，当螺旋桨转速n>800 r/min时，采用本文方法计算所得船模自由直航的航速与模型试验结果偏差小于0.5%；当螺旋桨转速n<800 r/min，所得航速的计算结果偏差有所增大，但均小于5%.

图9给出了螺旋桨转速n=820 r/min时，数值模拟所得自由面波形与试验结果的对比.从波形图像上看，所得结果是合理的.

图9 螺旋桨转速820 r/min时自由面波形图

3 结 论

1) 基于RANS方程，结合六自由度模型、VOF模型、整体区域动网格模型，采用体积力法构建虚拟桨模型，可较好地模拟船模的自由自航运动.

2) 虚拟桨的进流盘半径、偏移量对航速模拟均有影响，但进流盘半径是主要影响因素，偏移量对航速的影响不大.

3) 采用以进流盘半径为主要参数、偏移量为修正参数的设置方法，所得航速的计算精度可达0.5%，最大偏差小于5%.

[1]PABLO M, CARRICA T, ALEJANDRO M, et al. Self-propulsion computations using a speed controller and a discretized propeller with dynamic overset grids[J]. Journal of Marine Science and Technology,2010(15):316-330.

[2]RYAN G, COE A. Improved underwater vehicle control and maneuvering analysis with computational fluid dynamics simulations[D]. Virginia: Virginia Polytechnic Institute and State University,2013.

[3]ALEXANDER B, PHILLIPS C, STEPHEN R, et al. Evaluation of manoeuvring coefficients of a self-propelled ship using a blade element momentum propeller model coupled to a Reynolds averaged Navier Stokes flow solver[J]. Ocean Engineering,2009(36):1217-1225.

[4]RICCARDO B, GIULIO D. Simulation of turning circle by CFD: analysis of different propeller models and their effect on manoeuvring prediction[J]. Applied Ocean Research,2012(39):1-10.

[5]CHOI J E, KIM J H, LEE H G. Computational investigation of cavitation on a semi-spade rudder[J]. Journal of Marine Science and Technology,2010(15):64-77.

[6]吴召华.基于体积力法的船体自航性能数值预报[J].上海交通大学学报,2013,47(5):943-949.

[7]盛振邦.船舶原理[M].上海:上海交通大学出版社,2003.

Research on the Influencing Factors of Body Force Method in Numerical Simulation of Ship Self-propulsion

WU Hao OU Yongpeng XIANG Guo

(NavalEngineeringDepartment,NavalUniversityofEngineering,Wuhan430033,China)

In order to explore the applicability of body force method and its influencing factors in numerical simulation of ship model with free direct route, the body force method is applied to establish a virtual propeller model to investigate the influence of inflow plane radius and offset on the navigational speed of a double tail fin ship. The simulation results are compared with the free-running model test results. The results show that: the inflow plane radius has a greater impact on the navigational speed, while the offset has little effect on the navigational speed; based on the body force method, the errors of the numerical result can be limited to 0.5% and the maximum deviation is less than 5%.

numerical simulation; direct route; body force method; free running ship model

2017-02-11

*高性能船舶技术教育部重点实验室开放基金项目(2013033102)、工信部高技术船舶科研计划项目([2011]530)资助

U661.3

10.3963/j.issn.2095-3844.2017.02.019

吴浩(1987—)：男，博士生，主要研究领域为船舶与海洋结构物设计制造