基于RA结构的多元LDPC码编译码的实现
2017-06-05田晓燕蔡锁张锁良
田晓燕,蔡锁,张锁良
(河北大学 电子信息工程学院,河北 保定 071002)
基于RA结构的多元LDPC码编译码的实现
田晓燕,蔡锁,张锁良
(河北大学 电子信息工程学院,河北 保定 071002)
多元低密度奇偶校验(low density parity check,LDPC)码因具有比二元LDPC码更好的纠错性能、更强的抗突发错误能力及能与高阶调制相结合等特点而引起广泛关注.然而,多元LDPC码的诸多优点却被其高复杂度的编译码算法所限制.基于RA结构,构造出了具有快速编码算法的校验矩阵,采用双向递归流水线算法进行编码,并利用改进的EMS算法进行译码,降低了算法的复杂度和运算量,有利于硬件的实现.在加性高斯白噪声信道下,对GF(2)和GF(4)的LDPC码进行了性能比较,同时对GF(4) LDPC码在BPSK和4QAM调制下进行了对比.仿真结果证明了设计的正确性和可行性.
多元LDPC码;重复累积码;双向递归快速流水算法;扩展最小和算法
低密度奇偶校验(low density parity check,LDPC)码由Gallager于1962年首次提出[1],是一种具有稀疏校验矩阵的线性分组码.多元LDPC码由Davey和MacKay在1998年提出[2],作为二元LDPC码在伽罗华域的扩展,其具有更好的纠错性能、更高的抗突发错误能力及更适合与高阶调制系统相结合等优点.然而,多元LDPC码的诸多优点却因受到编译码复杂度高的限制而在实际中很难进行应用.多元LDPC码的构造方法分为随机构造法和结构性构造法2大类,常见的有Gallager构造法、渐近边增长(progressive edge-growth,PEG)算法、有限几何构造法等.但这些构造法用于硬件实现复杂度较高,不利于流水处理.多元LDPC码的译码算法有置信传播(belief propagation,BP)算法、基于快速傅里叶变换的置信传播(FFT-BP)算法和扩展最小和(extended min-sum,EMS)算法.这些算法的优点是译码效果好,但是计算复杂度和运算量比较大.针对上述问题,本文基于RA(repeat accumulate)结构[3],构造出具有快速编码算法的多元准循环LDPC码校验矩阵,并利用双向递归快速流水算法进行编码[4-5],编码效率和吞吐量都得到了提高;同时采用经过修正的EMS算法进行译码[6],虽然译码效果有所下降,但降低了运算复杂度,利于硬件的实现.
1 多元LDPC码构造
基于RA结构的多元LDPC码由重复器、交织器、加权器、组合器和累加器组成[7],编码流程如图1所示.

图1 RA结构编码系统Fig.1 Coding system of RA structure
设长为k的信息序列m=[m1,m2,…,mk],经重复器重复p次得
m1=m2=…=mp=[m1,m2,…,mk].
(1)
交织器由p个内交织的序列π1,π2,π3,…,πp组成,对信息序列m1=m2=…=mp完成交织,交织后输出序列B1,B2,…,Bp,将p个输出进行复合得
].
(2)
将复合后的A=[e1,e2,…,ek×p]输入到加权器、组合器模块,加权序列为W=[w1,w2,…,wk×p],组合器参数设为a,经过加权、组合操作后输出为
a.
(3)
经过累加器计算kp/a个校验位,设累加因子为α,β∈GF(q),则累加运算为
p1=r1·α-1,pi=(pi-1·β+ri)·α-1,i=2,3,…,kp/a.
(4)
由此得码字C=[m1,m2,…,mk,p1,p2,…,pkp/a],码率为a/(a+p).通过上述过程可以构造出校验矩阵H=[H1H2],其中H1的列重对应重复次数p,行重对应为组合参数a,非零元素分布由交织器参数决定,非零元素值由加权器决定.H2是由累加器决定的准双对角线矩阵.
2 快速编码算法
以码率为1/2的四元准循环LDPC码为例.设编码码组为C=[m1,m2,…,mk,p1,p2,…,pk],则C×HT=0.H矩阵为k×2k维的校验矩阵,设H=[H1H2]=[h1,h2,…,hk]T,H2的结构如图2所示,其中hi为1×2k维行向量.进行C×HT运算时,表示为
[0,0,…,0].
(5)
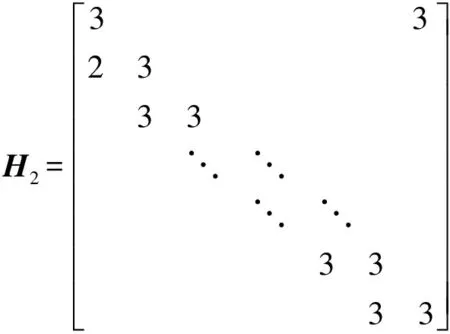
图2 校验矩阵的右半部分
Fig.2 Right part of the check matrix
由于GF(4)中,加法运算2+3=1,所以对于H2,所有列相加即[1,0,…,0].di代表校验矩阵中每一列中非零元素的和,所以上式可表示为
[m1,m2,…,mk,p1,p2,…,pk]×[d1,d2,…,dk,1,0,…,0]T=0,
(6)
从而得出校验位p1的表达式
).
(7)
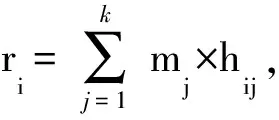
p2=(2·p1+r2)·2,pk=(3·p1+r1)·2,
(8)
p3=(3·p2+r3)·2,pk-1=(3·pk+rk)·2.
(9)
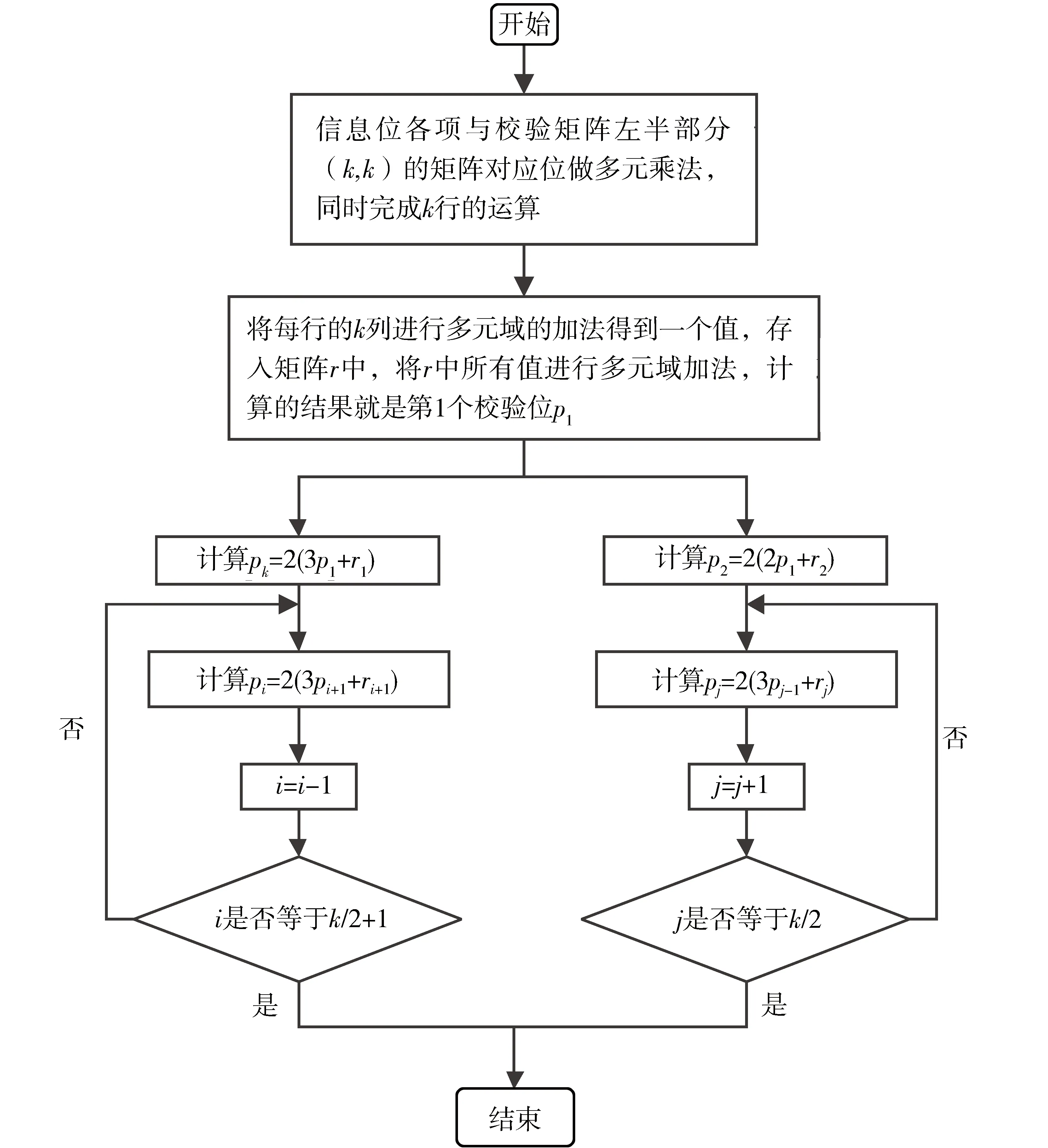
图3 双向递归快速编码算法流程Fig.3 Flow chart of fast double-recursion pipeline method
求出p1以后,可以用p1求p2和pk,然后用p2和pk求p3和pk-1,依次类推直到求出所有的校验位.这种双向递归快速流水编码算法大大加快了编码速度,可在实际中使用.对一个k×2k维、码率为1/2的具有RA结构的多元准循环LDPC码,采用上述编码算法的流程如图3所示,其中i的初始值为k-1,j的初始值为3,r是1×2k维的行向量.
3 可实现的EMS算法
本文采用了经过修正的EMS译码算法,使其利于硬件实现.首先计算初始化消息向量,对于一个GF(q)上的多元LDPC码,其信息位每位可能值有q个,所以码组中的每位需要用一组q维向量表示:
Lch=[Lch(0),Lch(1),…,Lch(k),…,Lch(q-1)].
(10)
对于码组中的任意位的任意1个域元素k,其消息向量的算法为
|yi-ki|2+|yi-s0|2),k=0,1,2,…,q-1,
(11)
其中s0为调制中0值对应的星座点,ki表示域元素k向量表示的第i个比特对应的调制星座点,yi表示编码码组向量表示的第i个比特对应的星座点经过高斯信道后接收到的值.
考虑到真正影响译码的是消息向量各元素之间的相对大小关系,所以对计算得到的消息向量全部减去消息向量中的最大值不影响译码结果.
设Lmax为向量Lch=[Lch(0),Lch(1),…,Lch(q-1)]的最大值,则经过减法得到的初始消息向量为
Lch=[Lch(0)-Lmax,Lch(1)-Lmax,…,Lch(q-1)-Lmax].
(12)
对向量进行排序,生成域元素向量Qch,与Lch中消息值一一对应,之后所有运算都将在消息向量与域元素向量之间展开,且均在保留所有域元素消息的前提下进行.
3.1 变量节点更新和置换
找出校验矩阵中每列的非零域元素,设更新运算中的单步运算子分别为消息向量A和I,相应的域元素向量为βA和βI,运算结果设为T,域元素向量为βT,运算如下:
T(i)=I(j)+A(k),
(13)
其主旨意思为:找到A中与I对应域元素相同的消息值相加,得到的T即为更新单步运算的结果,其对应的域元素为βT,且βT必为0至q-1之间的1个域元素.将所有的q个值全部运算完毕,接下来将得到的消息向量进行降序排列,域元素向量也需要对应的改变.最后将除搜索到的非零域元素位置的其他位置和初始消息的消息向量及域元素向量做上述运算,作为搜索到位置的消息、域元素更新值.至此完成对一个校验矩阵位置的填充,直到所有变量节点更新完成.变量节点向校验节点传递信息时会用到置换运算:将变量节点更新得到的域元素乘以校验矩阵对应位置的值.
3.2 校验节点更新和反置换
校验节点的更新是译码过程中运算最复杂且时间最长的.首先,找出校验矩阵中每一行的非零元素位置,其单步运算的运算子仍定义为I和A,运算结果设为B,与其相关的域元素向量为βI、βA和βB,运算如下:
(14)
其主旨意思为:将2个消息向量中对应域元素相加相同的消息值后,从这样一组值中找到最大值,作为消息值B(i),将域元素相加得到的值作为βB,且βB必为0至q-1之间的1个域元素.依照此法,将剩下的域元素及其对应的消息值算出,再将算出的消息值降序排列,域元素向量对应改变,单步运算完成.接下来将除搜索到的非零域元素位置的其他位置做上述运算,直到所有校验节点更新完毕.当校验节点向变量节点传递信息时会用到反置换:将校验节点更新得到的域元素除以校验矩阵对应位置的值.
3.3 译码判决输出
采用3.1步骤中的运算,将校验矩阵中每一列所有非零位置和对应初始消息的消息向量及域元素向量做运算,因为更新后的消息向量都经过降序处理,所以域元素向量的第1个元素即可能性最高的域元素,把域元素向量的第1个元素作为判决输出,若译码结果满足C×HT=0,则译码完成,否则继续以上步骤.其流程如图4所示.
4 性能分析
用随机产生的信息位分别对(60×120)RA结构四元准循环LDPC码以及(120×240)二元LDPC码进行了仿真,调制方式为BPSK,通过加性高斯白噪声信道,译码最大迭代次数设置为20次,帧长为150 000帧.得出误码率的性能曲线如图5所示.
从图5中可以看出,在相同码长的条件下四元LDPC码整体的误码率要比二元的好,这就是多进制LDPC码引起人们关注的原因.
对于多元LDPC码,在编码完成后,码组将被输入调制系统中.下面对4QAM与BPSK 2种不同调制下的译码性能进行了比较[8],如图6所示.
采用4QAM调制时,误码率随信噪比的增加,降低速度比较快,整体表现出较好的译码性能.相比于BPSK调制,它的误码率同时达到10-5量级,4QAM相比于BPSK,可提供1 dB的编码增益.在实际信息传输中,采用4QAM的高阶调制时对信道环境的要求更低,并且能够更好的控制误码.
本文设计的具有RA结构的多元准循环LDPC码不仅具有多元码型自身所特有的抗突发错误特性,并且可以采用双向递归快速算法进行编码,能进行流水处理.同时采用改进的EMS算法进行译码,降低了译码复杂性,便于硬件的实现.此外,RA结构的LDPC码自身具有交织特性,使其抗突发错误与纠错的特性进一步提高.本文讨论的RA结构多元LDPC码具有比较大的研究和工程应用价值.
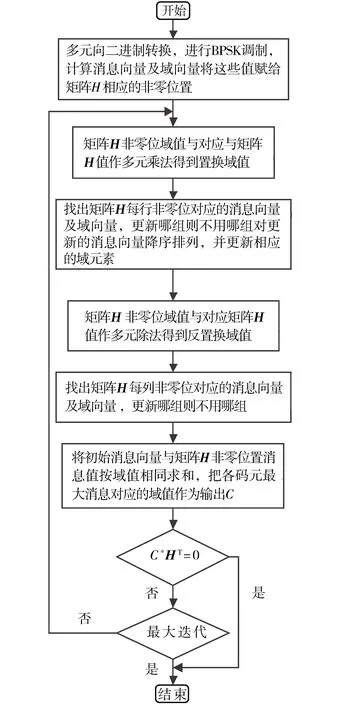
图4 EMS译码算法流程Fig.4 Flow chart of EMS decoding algorithm
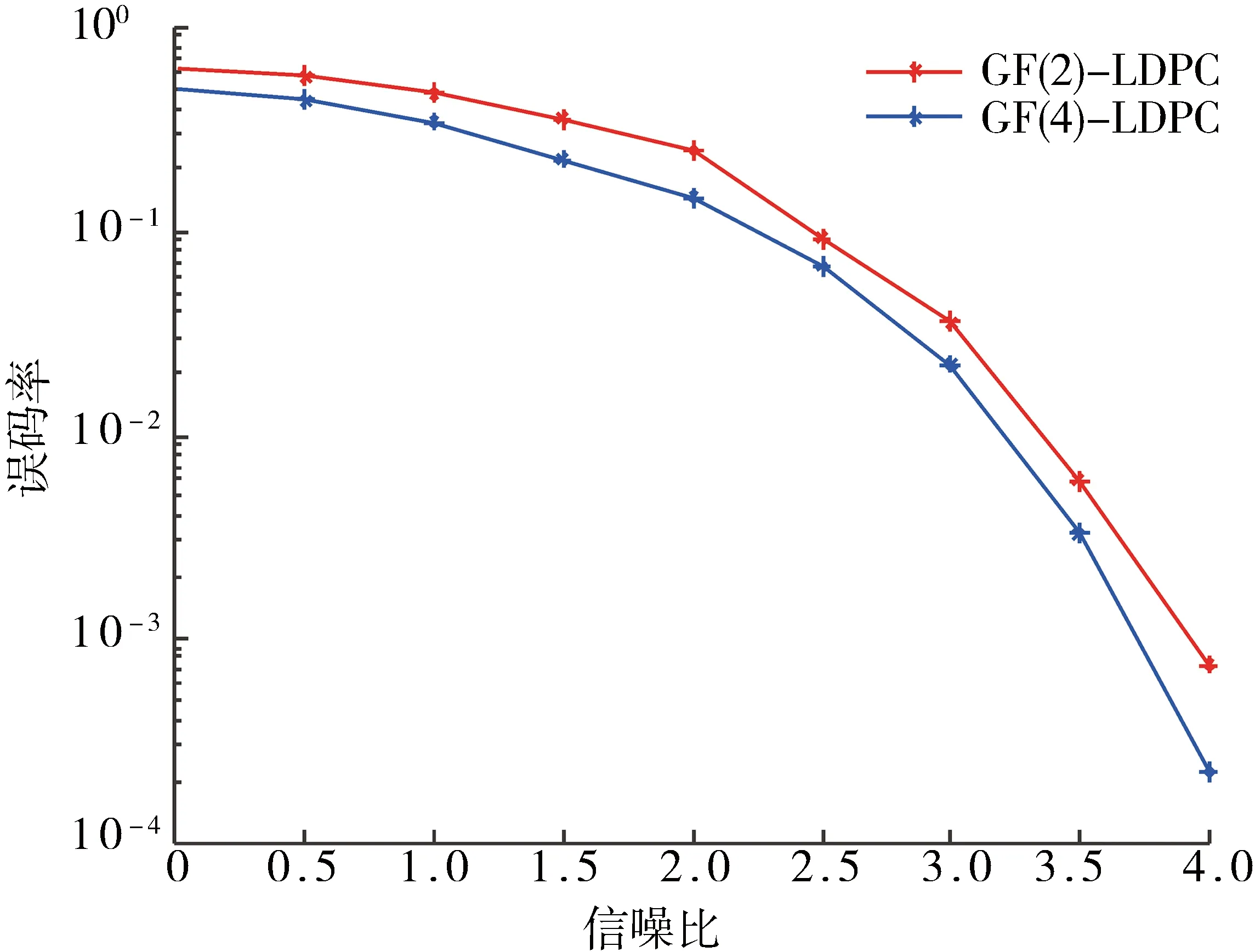
图5 LDPC码性能比较Fig.5 Performance comparison of LDPC
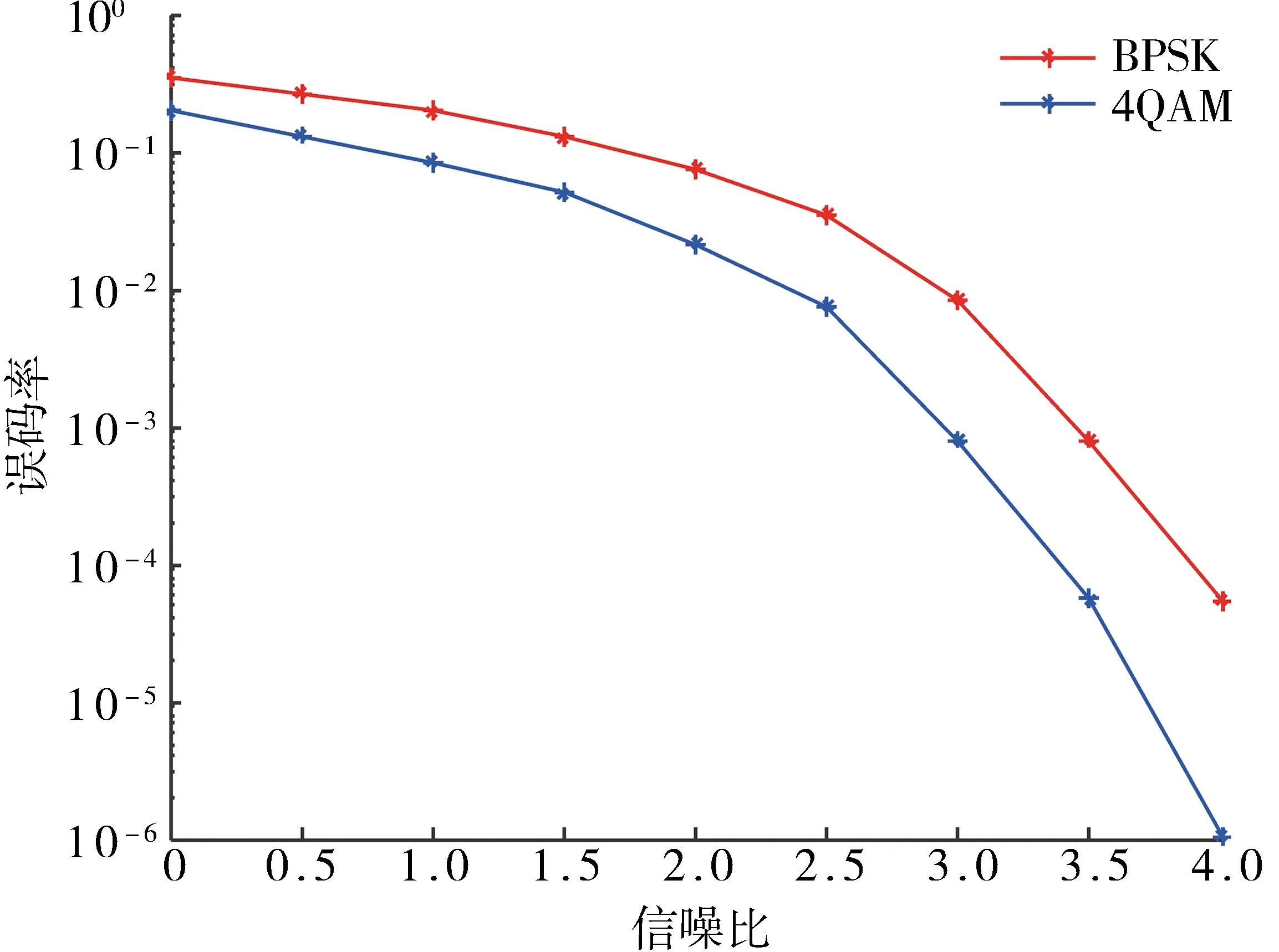
图6 RA结构不同调制下的性能比较Fig.6 Performance comparison of RA structure with different modulations
[1] GALLAGER R G.Low-density parity-check codes [J].IRE Trans Information Theory,1962,8(1):21-28.
[2] DAVEY M C,MACKAY D J C.Low density parity check codes over GF(q) [J].IEEE Commun Lett,1998,2(6):165-167.
[3] JOHNSO S J,WELLER S R.Combinatorial interleavers for systematic regular repeat-accumulate codes [J].IEEE Transactions on Communications,2008,56(8):1201-1206.
[4] 袁瑞佳,白宝明,童胜.10 Gbps LDPC编码器的FPGA设计[J].电子与信息学报,2011,33(12):2942-2947.DOI:10.3724/SP.J.1146.2010.01338. YUAN R J,BAI B M,TONG S.FPGA-based design of LDPC encoder with throughput over 10 Gbps [J].Journal of Electronics & Information Technology,2011,33(12):2942-2947.DOI:10.3724/SP.J.1146.2010.01338.
[5] 张博,林伟,刘春元,等.突发错误信道下的多元LDPC码设计与性能分析[J].通信学报,2013,34(7):98-104.DOI:10.3969/j.issn.1000-436x.2013.07.011. ZHANG B,LIN W,LIU C Y,et al.On the designand performance of nonbinary LDPC codes on burst errorchannels [J].Journal on Communications,2013,34(7):98-104.DOI:10.3969/j.issn.1000-436x.2013.07.011.
[6] ZHAO S C,LU Z F,MA X,et al.A variant of the EMS decoding algorithm for nonbinary LDPC Codes [J].IEEE Communications Letters,2013,17(8):1640-1643.
[7] 张红泰,刘宏立,刘述刚.基于满二叉树的RA码交织器设计[J].计算机工程与科学,2015,37(4):699-703.DOI:10.3969/J.issn.1007-130X.2015.04.012. ZHANG H T,LIU H L,LIU S G.Interleaver design for RA codes based on full binary tree [J].Computer Engineering & Science,2015,37(4):699-703.DOI:10.3969/J.issn.1007-130X.2015.04.012.
[8] 吕岩,李劲.通用PSK和QAM解调接收机[J].河北大学学报(自然科学版),2013,33(2):204-209.DOI:10.3969/j.issn.1000-1565.2013.02.017. LU Y,LI J.Universal PSK and QAM demodulation receiver [J].Journal of Hebei University(Natural Science Edition),2013,33(2):204-209.DOI:10.3969/j.issn.1000-1565.2013.02.017.
(责任编辑:王兰英)
Encoder and decoder realization of non-binary LDPC codes based on RA structure
TIAN Xiaoyan,CAI Suo,ZHANG Suoliang
(College of Electronic and Information Engineering,Hebei University,Baoding 071002,China)
Compared with binary LDPC codes,non-binary codes have better error correction performance,stronger burst-error-correcting capability,can also combine with higher-order modulations,which attracted a wide-spread attentiaon.However the advantages of non-binary LDPC codes are limited by the high complexity of encoding and decoding algorithm.Based on repeat accumulate structure,a check matrix with fast algorithm was constructed.By using fast double-recursion pipeline method and improved EMS decoding algorithm,complexity and calculation of the algorithm were reduced,which are beneficial for the realization of the hardwares.On Gaussian channel,the BER of GF(2) and GF(4) LDPC codes are compared,and the modulation performance of BPSK and 4QAM are compared for GF(4) LDPC.Simulation results prove the validity and feasibility of the design.
non-binary LDPC codes;repeat accumulate codes;fast double-recursion pipeline method;EMS algorithm
2016-04-28
河北省自然科学基金资助项目(F2011201045)
田晓燕(1980—),女,河北衡水人,河北大学讲师,主要从事信道编译码与信息处理方向的研究. E-mail:458664731@qq.com
张锁良(1966—),男,河北藁城人,河北大学教授,主要从事高速数据通信方向的研究.E-mail:zhangsl@hbu.cn
10.3969/j.issn.1000-1565.2017.03.015
TN919
A
1000-1565(2017)03-0316-06
