复合摆线少齿差行星传动的啮合性能分析*

石万凯 徐浪 韩振华 常帅

(重庆大学 机械传动国家重点实验室, 重庆 400044)

复合摆线少齿差行星传动的啮合性能分析*

石万凯 徐浪 韩振华 常帅

(重庆大学 机械传动国家重点实验室, 重庆 400044)

采用几何特性可调性强的复合摆线作为内齿廓，根据微分几何和齿轮啮合原理,按照少齿差运动规律,建立啮合方程以及共轭齿廓方程,并推导了齿轮副的啮合线、重合度、啮合界限、根切条件.分析了齿轮副诱导法曲率、压力角以及齿形调节系数对齿轮压力角的影响，设计并建立了齿轮副三维实体模型,进行了动力学仿真,模拟一定工况下齿轮副运动关系及传递效率.结果表明，复合摆线少齿差行星传动具有多齿啮合、传动压力角小、齿轮副诱导法曲率小、传动效率高等优良的啮合性能.

复合摆线；少齿差；行星传动；啮合原理；啮合性能

摆线行星传动具有传动比大、结构紧凑、承载能力强和传动效率高等优点,广泛应用于各工业领域.用作少齿差精密传动时具有扭转刚度大、多齿啮合误差均化效应好、传动精度高等优良特性,越来越受到重视.国内外不少学者在摆线传动的理论与应用方面进行了大量研究.Litvin等[1]和Vecchiato等[2]根据微分几何和齿轮啮合原理对摆线针轮啮合理论、包络存在条件以及共轭曲面避免奇点条件等进行了研究;Chen等[3]运用包络法建立了摆线针轮行星传动正/负一齿差、二齿差、三齿差等典型少齿差行星传动的共轭啮合理论体系;Nam等[4]研究了一种梯形齿廓用作少齿差精密传动时的性能;Hsieh[5]根据啮合原理对一种椭圆滚摆线应用于转子泵进行了研究并和传统圆摆线转子泵进行了对比分析;Demenego等[6]对摆线齿轮泵的齿形设计、根切条件和接触特性进行了研究;Liu等[7]对由摆线和圆弧组合的齿廓做少齿差传动时的啮合特性进行了分析;Li[8]对摆线针轮行星传动齿轮副进行了设计并分析了其强度.陈兵奎等[9]设计了一种抛物线型二次包络行星减速器.

虽然研究者们针对摆线行星传动进行了大量研究,但是摆线少齿差行星传动压力角、诱导法曲率等啮合特性改善有限.本研究利用几何形状可调性强的复合摆线作为齿廓,建立复合摆线齿轮少齿差行星传动啮合理论,分析其传动特性，进行新型齿廓共轭传动理论研究,为新型高性能齿轮的实际应用提供理论技术指导,加速其应用进程.

1 复合摆线

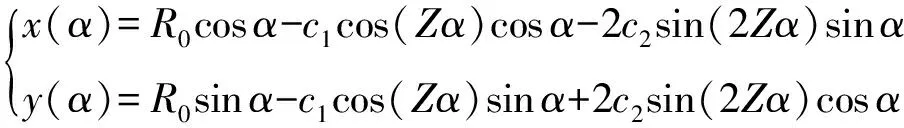
(1)

式中,R0为分布圆半径,Z为齿数,c1为齿高调节系数,c2为齿形调节系数,α为复合摆线上点位置参数.R0、c1对复合摆线齿轮副外形尺寸的影响分别与摆线针轮传动中针齿分布圆半径、针齿半径相同.

当取R0=45,Z=16,c1=8,c2=1.4，1.0，0.6，0.2时,求解出复合摆线齿形，如图1所示.

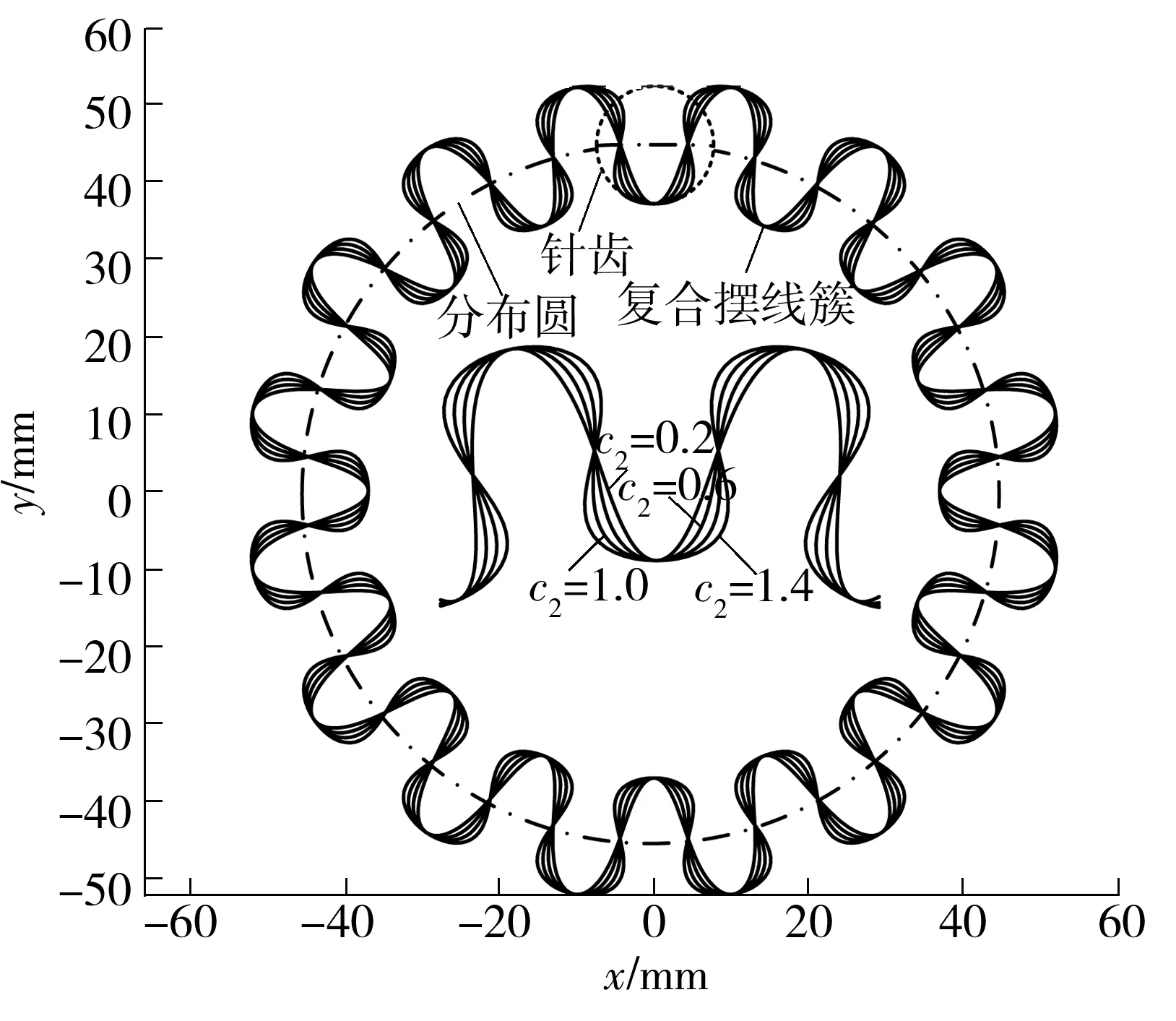
图1 复合摆线齿形随c2的变化

由图1可知，当复合摆线齿廓其他参数保持不变时,随着c2的减小,齿廓由尖陡形逐渐过渡到宽胖形.与普通摆线轮相比,齿形变化范围广,具有较明显的差异.

2 复合摆线行星传动共轭理论

2.1 啮合原理及坐标变换

采用运动学法求解复合摆线齿轮的共轭齿廓,通过机构反转法将复合摆线少齿差传动系统转化成定轴传动.根据右手法则建立坐标系(见图2),固定坐标系Sf(xf,yf,zr)、Sp(xp,yp,zp)与箱体固联,动坐标系S1(x1,y1,z1)、S2(x2,y2,z2)分别与复合摆线内齿轮1、共轭行星齿轮2固联,轴zp、轴z1和轴zf、轴z2分别与齿轮1、2的中心轴线重合,坐标系S1到坐标系S2、Sp的坐标变换矩阵分别为M21、Mp1.

齿轮副偏心距为a,传动比为i21,齿数分别为Z1、Z2,齿轮1分布圆半径为R01,角速度大小分别为ω1、ω2,方向如图2所示.初始时刻,坐标系S1和Sp重合，S2和Sf重合,经过时间t后,齿轮1、2转过的角度分别为φ1、φ2.根据运动关系,可得:

i12=ω1/ω2=Z2/Z1=φ1/φ2=1/i21

(2)

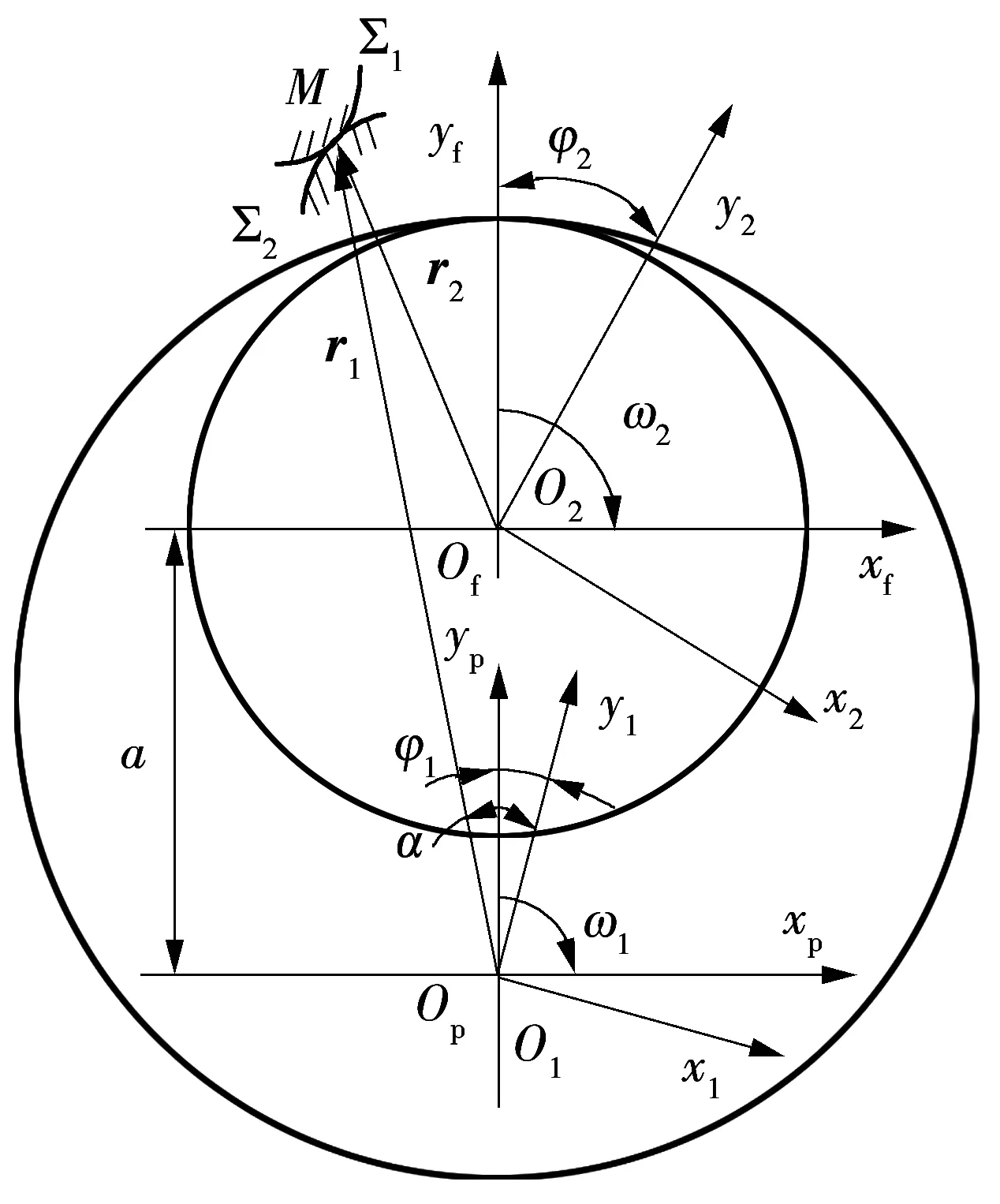
图2 共轭坐标系

由第1节可得四阶复合摆线齿轮齿廓曲线在坐标系S1中的曲线方程如下:

r1(α)=[x1(α) y1(α) 1]T=

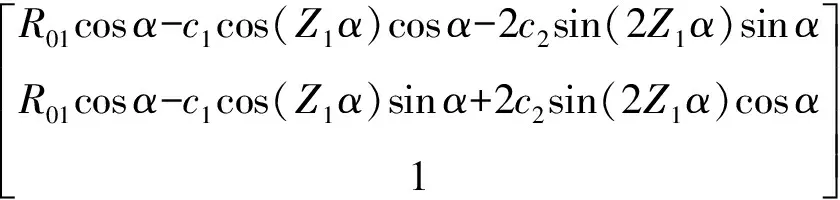
(3)

其中,α∈(0,2).

根据啮合原理[11]可得齿轮副共轭啮合方程:

(4)

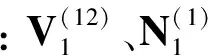
(5)

(6)

各式中下标1表示在坐标系S1中.

坐标系S1中齿廓∑1上啮合点M1到坐标系S2中齿廓∑2上啮合点M2的坐标变换为

r2(α,φ1)=M21(φ1)r1(α)

(7)

联立式(4)、(7)可以求得坐标系S2中齿廓∑2的方程:

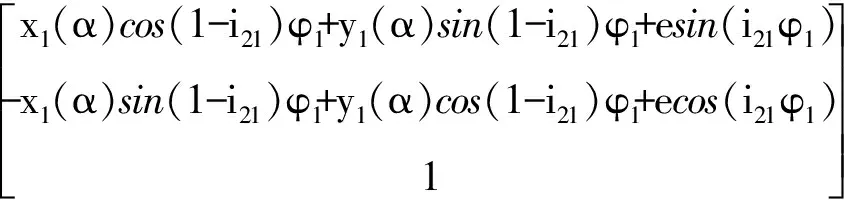
(8)

啮合线是啮合点在定坐标系中的轨迹.坐标系S1中齿廓∑1上啮合点M1到坐标系Sp中啮合线∑m上啮合点M的坐标变换为

rm(α,φ1)=Mp1(φ1)r1(α)

(9)

联立式(4)、(9)可以求得在坐标系Sp中啮合线∑m的方程：

(10)

取一对复合摆线齿轮副参数如表1,求解得其复合摆线内齿廓及共轭齿廓如图3,啮合线如图4.

表1 复合摆线少齿差行星传动齿轮副参数

Table1Parametersofthecompositecycloidgearsofsmallteethdifferenceplanetarytransmission

R0/mmZ1Z2c1/mmc2/mma/mm45161580．82

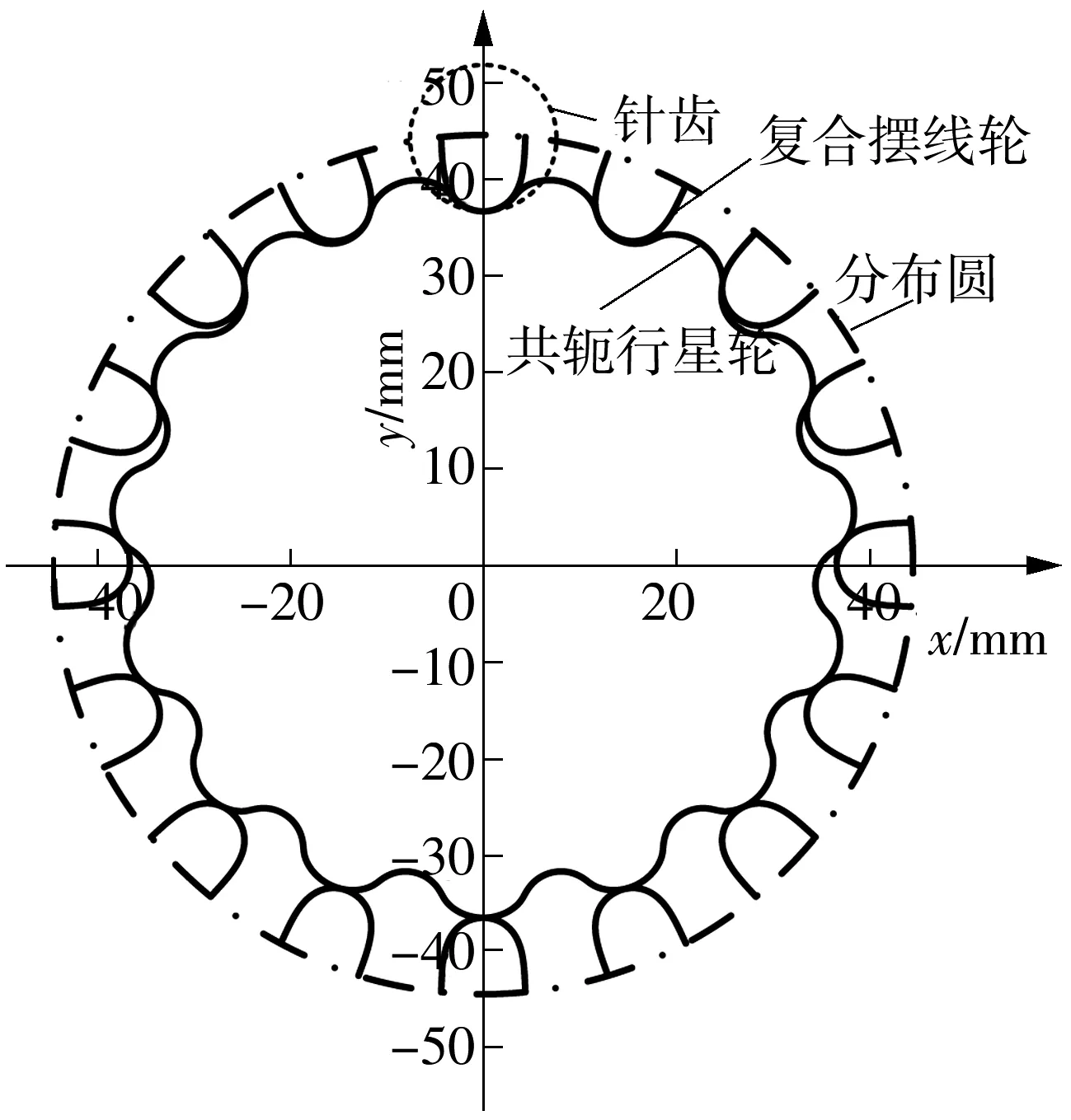
图3 复合摆线内齿廓和共轭齿廓

Fig.3 Composite cycloid tooth profile and the conjugate tooth profile

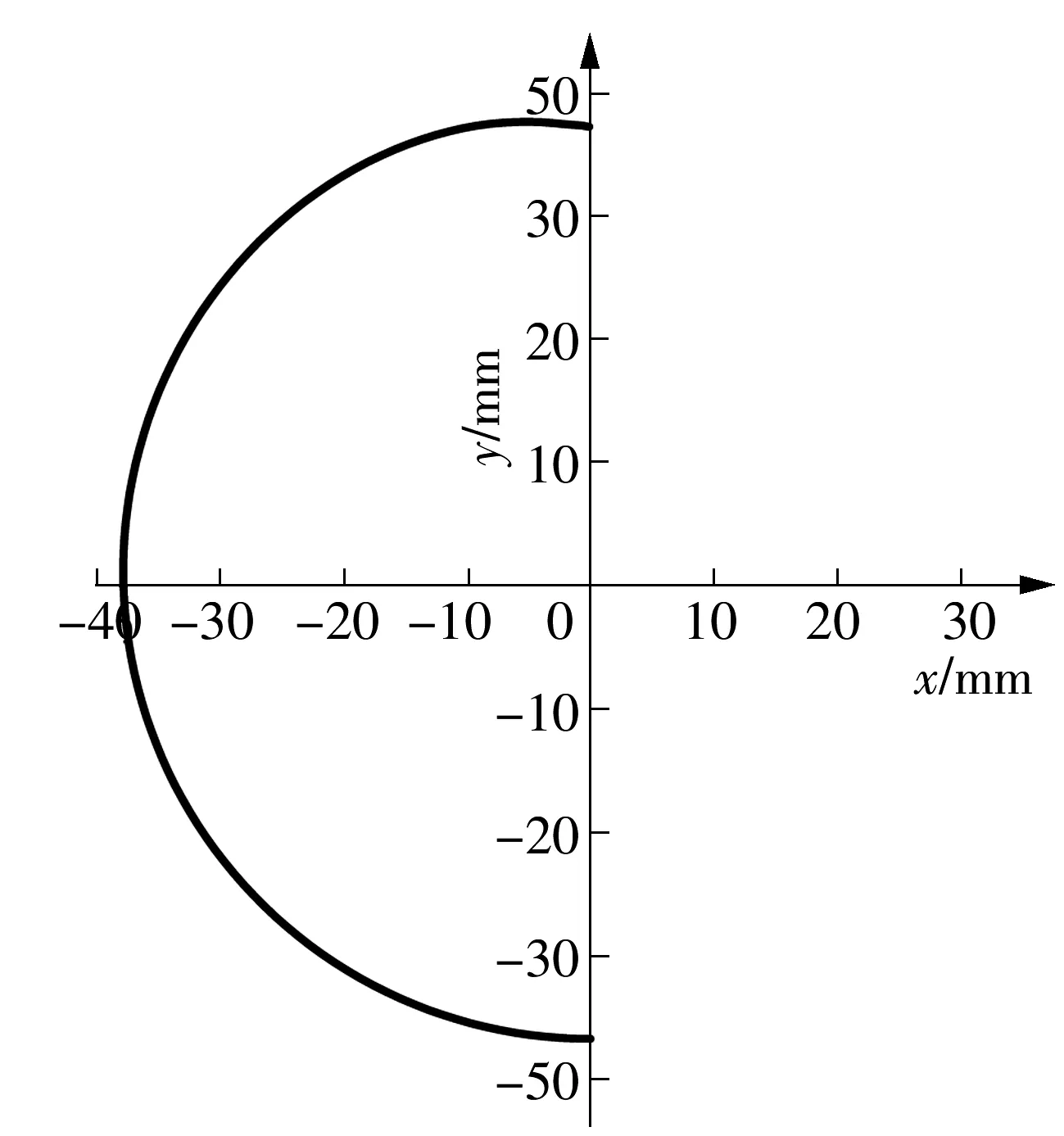
图4 啮合线

如图4所示,啮合线近似一个半圆,说明复合摆线齿轮副做少齿差行星传动时理论条件下有一半齿同时进入啮合,重合度大,运动传递平稳;同时多齿啮合,齿轮副啮合刚度大,传动强度高,并且具有误差均化效应,可以应用于少齿差精密传动领域.

2.2 重合度

根据齿轮啮合原理复合摆线少齿差行星传动的重合度可定义为:复合摆线共轭行星轮齿单侧齿面从齿根啮合到齿顶过程中,同时参与啮合的齿数[3].由啮合线所对应的转角计算其重合度的公式为

ε=θ1Z1/2

(11)

式中，θ1=Z2ψmax/(Z1-Z2),为啮合线所对应的复合摆线轮转角,ψmax为行星轮齿单侧齿廓对应圆心角，一齿差时ψmax=/Z2,因此ε=Z1/2.

2.3 啮合界限

复合摆线齿轮副啮合过程中内齿轮齿廓曲线上的点并不全部参与啮合,实际参与啮合的只有齿顶附近的部分区域.所以,该段曲线的几何形状对齿轮副的传动性能起主要决定作用.由啮合方程(式(4))可得复合摆线内齿轮齿廓曲线上啮合点位置参数α与其转角φ1的函数关系[2]:

α=g(φ1)

(12)

将函数对φ1求导,

(13)

令g′(φ1)=0，联立啮合方程(式(4)),即可求出g(φ1)在一个齿廓啮合范围内的两个极值点,则可确定复合摆线内齿轮齿廓曲线上实际参与啮合的曲线段.通过调节齿形参数c2，从而改变该段曲线的曲率、开合程度，即可实现对齿轮副传动性能的改变.

根据表1中参数,求解出复合摆线齿轮副啮合界限(见图5).由图可知,复合摆线齿轮齿廓曲线上实际进入啮合的只有齿顶处的一小段,而复合摆线齿形是狭长形,受力易变形,单齿对啮合刚度小,轮齿齿根弯曲强度低.在不产生齿廓干涉的条件下,相邻两齿间齿根用一段圆弧平滑过渡(见图6),以降低齿高,增大齿轮副啮合刚度和复合摆线内齿轮齿根弯曲强度,从而改善齿轮副传动强度,提高齿轮副传动精度.

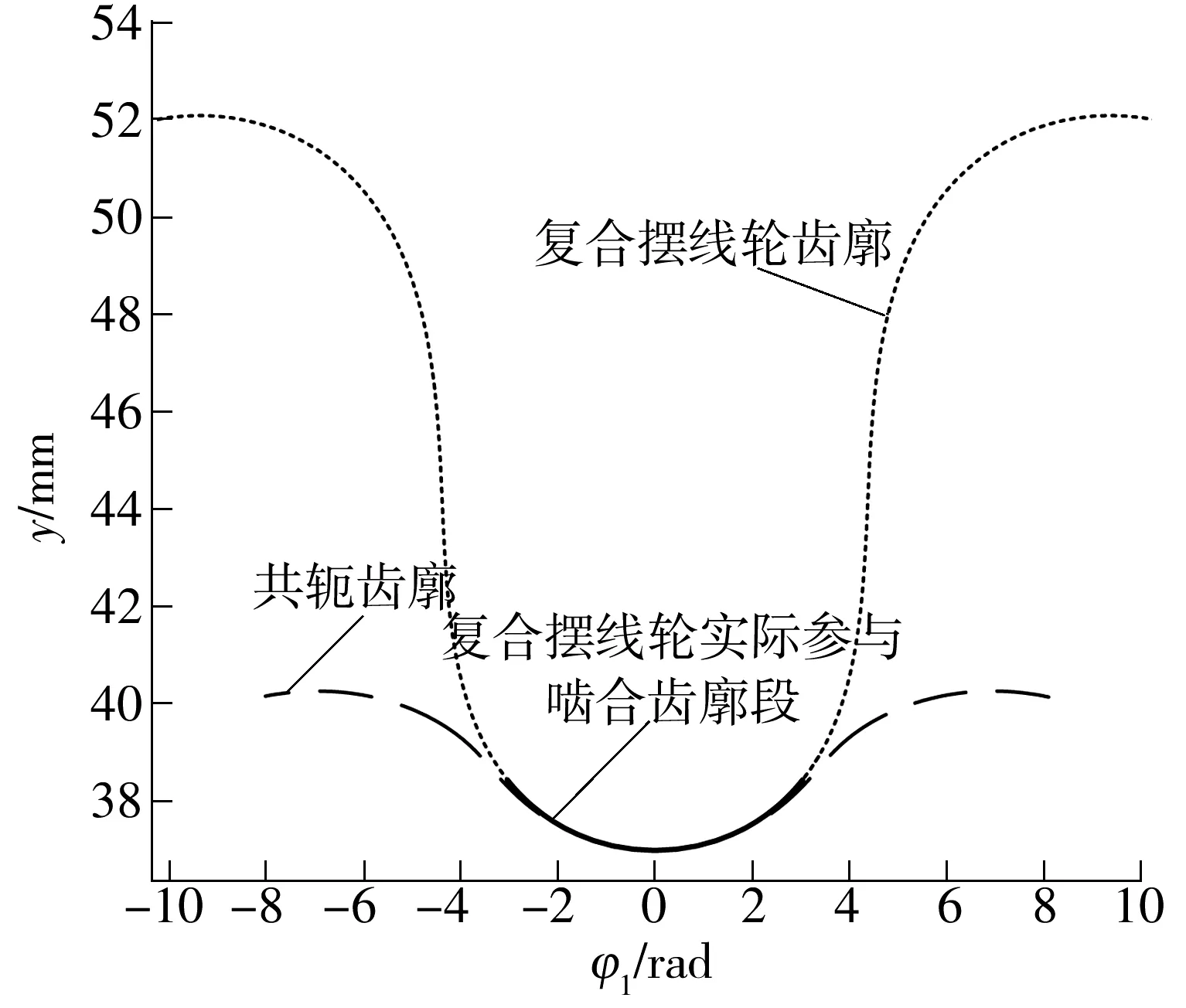
图5 啮合界限

图6 齿根圆角过渡复合摆线轮与共轭行星轮

Fig.6 Root filleted composite cycloid gear and conjugate planetary gear

当表1中其他参数保持不变时,c2分别取1.4、1.0、0.6、0.2时,分别计算出复合摆线齿轮啮合界限点的位置参数αmax与c2的关系(见表2),复合摆线啮合段齿廓位置参数α随c2的变化见图7,齿轮副齿形随c2变化情况见图8.

表2 啮合界限点的展角αmax与c2的关系

Table 2 Relationship between location angleαmaxof the boundary point andc2

c2αmax/radc2αmax/rad1．40．04140．60．03831．00．04030．20．0342

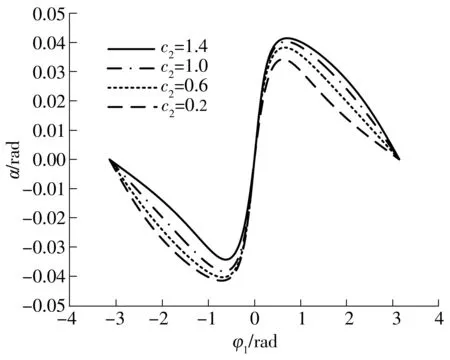
图7 复合摆线轮啮合区域齿廓展角α随c2的变化

Fig.7 Locating angleαof composite cycloid gear meshing area change along withc2

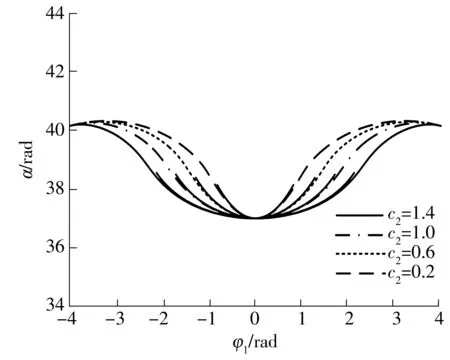
图8 齿轮副齿形随c2的变化

从表2和图7可以看出,啮合界限点的位置角αmax随着c2的减小而减小,复合摆线轮实际参与啮合的曲线段越来越短，为了减缓齿面磨损，延长保精寿命，c2不宜取太小.在一个齿廓啮合周期内,复合摆线轮齿廓展角α绝对值从0先增大到αmax，然后减小到0,说明单侧齿廓上的点都先后两次进入啮合.

由图8可知,随着c2的减小,复合摆线轮齿形越来越窄陡,力学性能越来越差,而共轭行星轮齿廓齿厚越来越厚,齿槽越来越窄.因此,c2过大或过小都会使齿厚和齿槽宽不协调,影响齿轮副综合力学性能.所以,复合摆线齿轮副应用于少齿差行星传动时c2取值0.5～1.0为宜.

2.4 根切条件

共轭的齿轮副要实现正确、平稳的运动传递和良好的传动性能,只满足共轭啮合条件是不够的.复合摆线共轭齿廓防止根切对于提高齿轮副的寿命、避免齿廓干涉以及共轭齿廓的加工可行性均具有重要意义.假设齿廓∑1是用来加工齿廓∑2的刀具齿面,如齿廓∑2上出现奇点,则该点进入啮合位置时,沿齿廓∑2运动的速度为零[12].即:

(14)

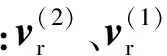
(15)

将啮合方程(式(4))对时间t求导可得:

(16)

(17)

其参数矩阵如下:

(18)

要使方程组有非零解,必须使参数矩阵A的秩为1,因此可以得出根切函数:

(19)

若Ф=0,则参数矩阵A的秩为1,方程组(17)有非零解,则齿廓∑2出现了奇点,可能发生根切,否则齿廓∑2上不会根切.取ω1=1(ω1为非零公因子,取值不影响Ф的符号),根据表1中参数,计算得根切函数值如图9所示.

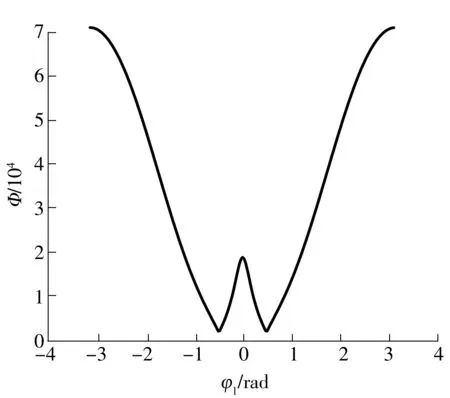
图9 根切函数值

由图9可知,齿轮副根切函数值Ф始终大于0,即表明共轭齿廓∑2不存在奇点,齿廓没有发生根切.

3 传动特性

3.1 压力角

压力角作为评价齿轮传动性能好坏的重要参数,对齿轮副几何尺寸、受力情况以及传动强度等有着很重要的影响.压力角是齿廓上点的法线方向与该点线速度方向的夹角(见图10).如图所示,齿轮副在M点进入啮合时,压力角αg2可由下式计算:

(20)

(21)

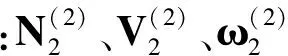
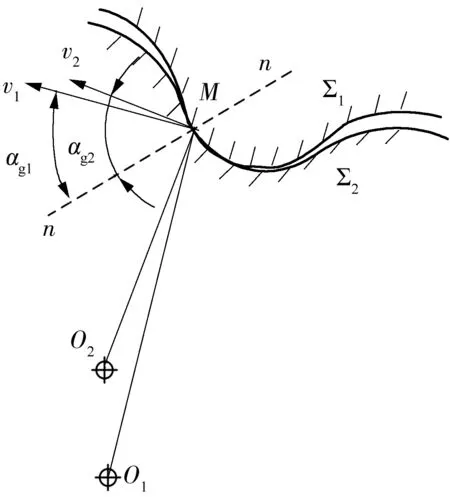
图10 齿轮副压力角

普通摆线传动外形尺寸确定时齿廓压力角也确定了,而复合摆线齿轮副外形尺寸确定时(R0、Z1、c1确定)则可调节齿形参数c2来改变齿廓曲线开闭程度以及曲率,从而来改变齿轮压力角等特性，影响齿轮传动效果.当表1中其他参数不变时,齿形参数c2分别取1.4、1.0、0.6、0.2时,计算出压力角αg2随c2变化情况如图11所示.

由图11可知，复合摆线共轭齿轮压力角比普通摆线齿轮压力角小,压力角最小值下降幅度最小为16.1%,并且在主要传力区域压力角αg2的值随着c2的减小而减小,齿轮副传力性能进一步改善.

3.2 诱导法曲率

诱导法曲率是两共轭曲面法曲率的差值,表征两共轭曲面的贴近程度,直接影响齿面摩擦磨损、润

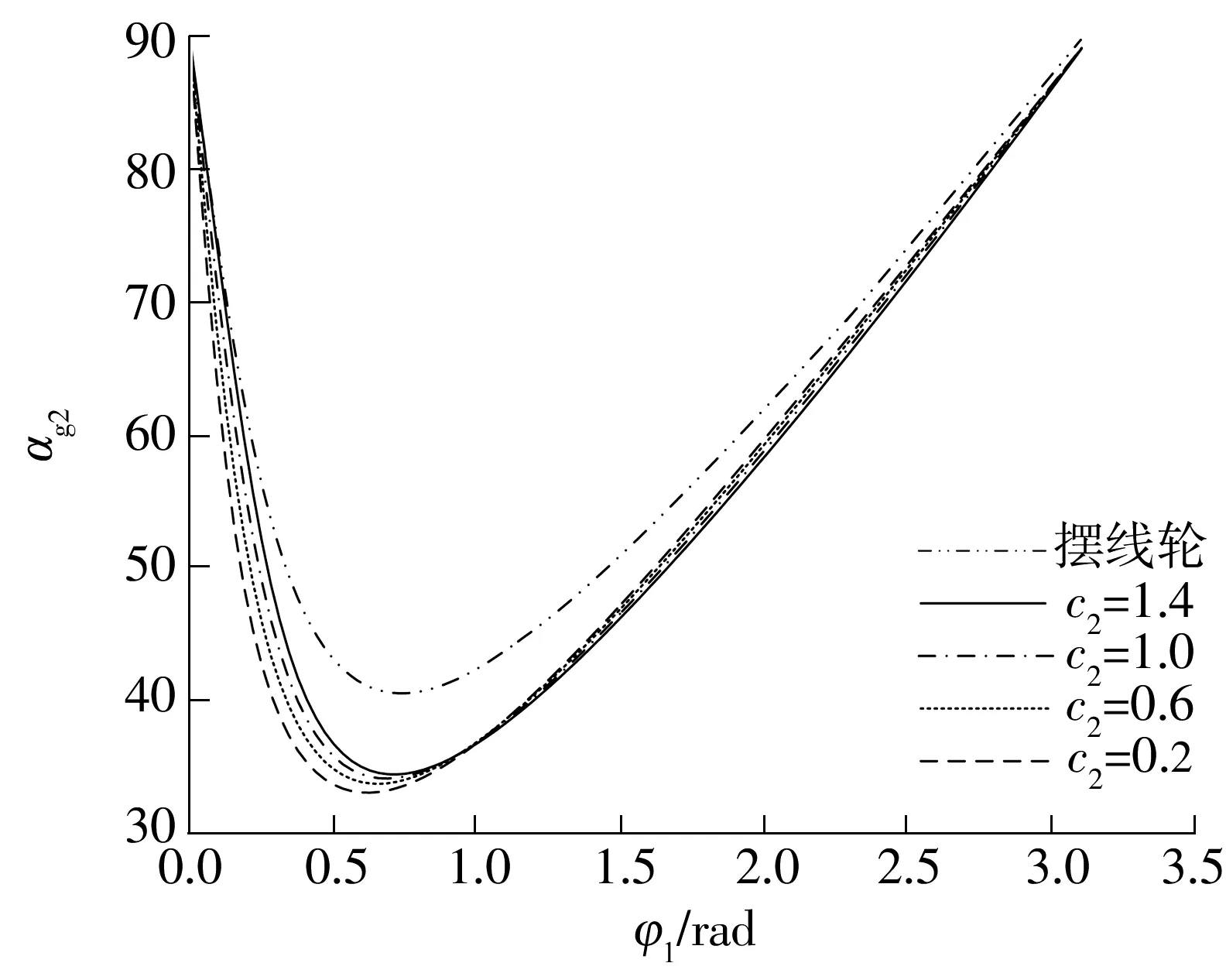
图11 压力角随c2的变化

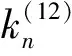
(22)

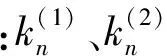
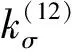
(23)

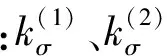
(24)

(25)

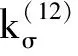
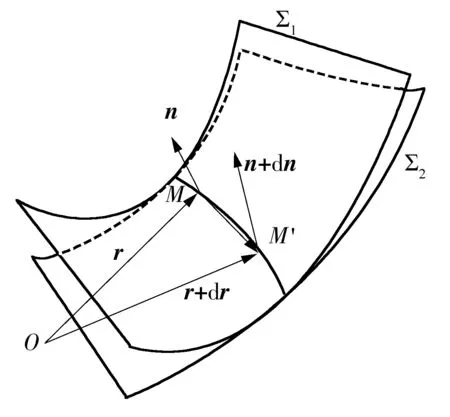
图12 线接触两齿面

图13 诱导法曲率

4 动力学仿真

4.1 三维实体建模

根据复合摆线齿轮共轭理论,建立齿轮副三维精确实体模型.文中所分析的复合摆线少齿差行星传动齿轮副的基本参数如表 1 所示,齿轮副齿宽为10 mm.计算出齿轮齿形点云数据,将齿轮齿形点云数据导入三维建模软件中,创建精确的三维实体模型如图14所示.采用实体模型进行运动仿真,仿真结果显示齿轮副可以实现连续无干涉传动,表明齿廓设计正确.

4.2 动力学仿真

将4.1节建立的齿轮副和偏心轴按设计几何形位要求装配,将装配体三维模型导入ADAMS中,添加约束,建立复合摆线齿轮副少齿差行星传动动力学仿真模型(见图15),模型约束情况如表3所示.

根据弹性接触理论,静态接触时法向力F和变形δ关系[14- 15]为

F=Kδ3/2

(26)

式中，K为接触物体间碰撞刚度,与撞击物体材料和结构形状相关.

(27)

其中，

(28)

(a)齿根圆角过渡复合摆线内齿轮

(b)共轭行星齿轮

(c)复合摆线齿轮副

图15 复合摆线少齿差行星传动动力学仿真模型

Fig.15 Dynamic simulation model of the composite cycloid small teeth difference planetary transmission system

表3 仿真模型约束情况表

(29)

其中:R1、R2是两齿轮在碰撞接触点的曲率半径(由图13可知,齿轮副齿廓曲率变化不大,均以其曲率半径均值作为接触时曲率半径)；μ1、μ2、E1、E2分别是两接触物体材料泊松比和弹性模量.

ADAMS中用Impact碰撞力函数模拟动态接触力[16]:

F=Kδe+step(δ,0,0,δmax,Cmax)dδ/dt

(30)

式中，碰撞接触刚度K由式(26)计算,力指数e由式(26)可得,刚体碰撞阻尼系数C一般取一个较小的值.

复合摆线轮和共轭齿轮材料为GCr15,弹性模量为2.1×105MPa,泊松比0.3.则可算得复合摆线齿轮副接触冲击刚度K=2.27×105N/m3/2,力指数e为1.5,阻尼系数C取30N·s/mm,接触中考虑摩擦力,静摩擦系数取0.1,动摩擦系数取0.05,静态阻力滑移速度取0.1mm/s,动态阻力转换速度取10mm/s[16].

给偏心轴施加9 000°/s的恒定角速度;给共轭行星齿轮施加7.5×104N·mm的恒定扭矩.仿真步数取4.0×103,时间取0.04s.得到仿真结果如图16-19所示.

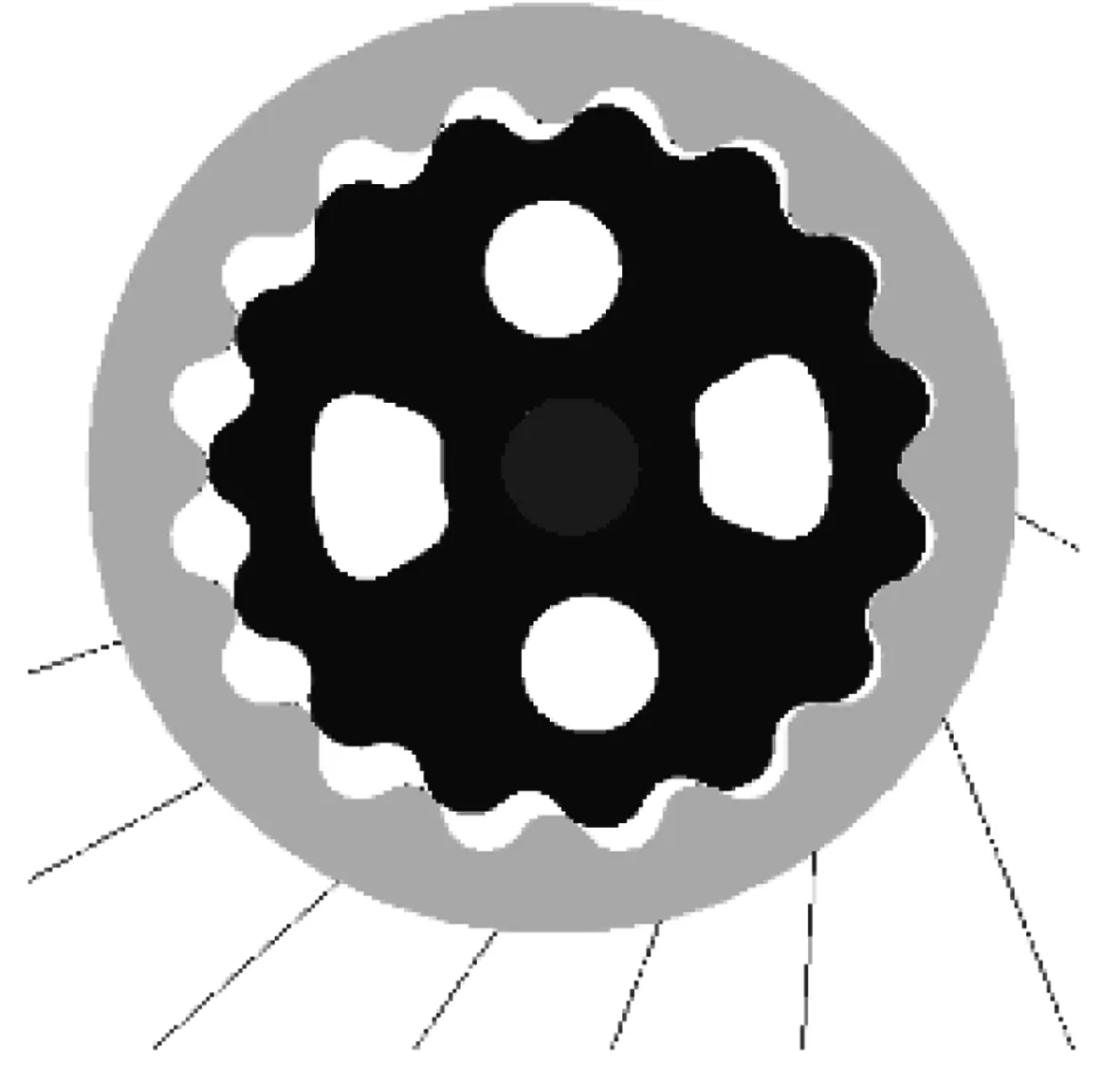
图16是齿轮副某一瞬时的仿真受力情况，可以看出在该瞬时有8对齿间有作用力，半数齿参与啮合，重合度大,与理论计算一致.

根据少齿差行星传动原理,在偏心轴输入转速为9 000 °/s时,共轭行星轮理论输出转速应为600°/s.

由图17可知,行星轮输出转速在理论转速上下小幅波动,其平均值为599.99 °/s,与理论值误差为0.00 17%.偏心轴理论输入转矩应为5 000N·mm.

由图18可知,偏心轴输入转矩存在一定的波动,其平均值为5 390.20N·mm,与理论值误差为7.8%.由效率公式η=Toutnout/(Tinnin)求得齿轮副的传动效率为 92.8%.

(a)全局视图

(b)局部放大视图

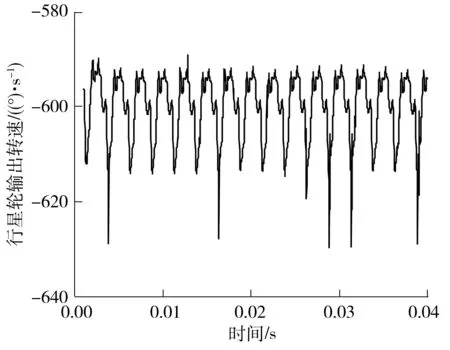
图17 共轭行星轮输出转速

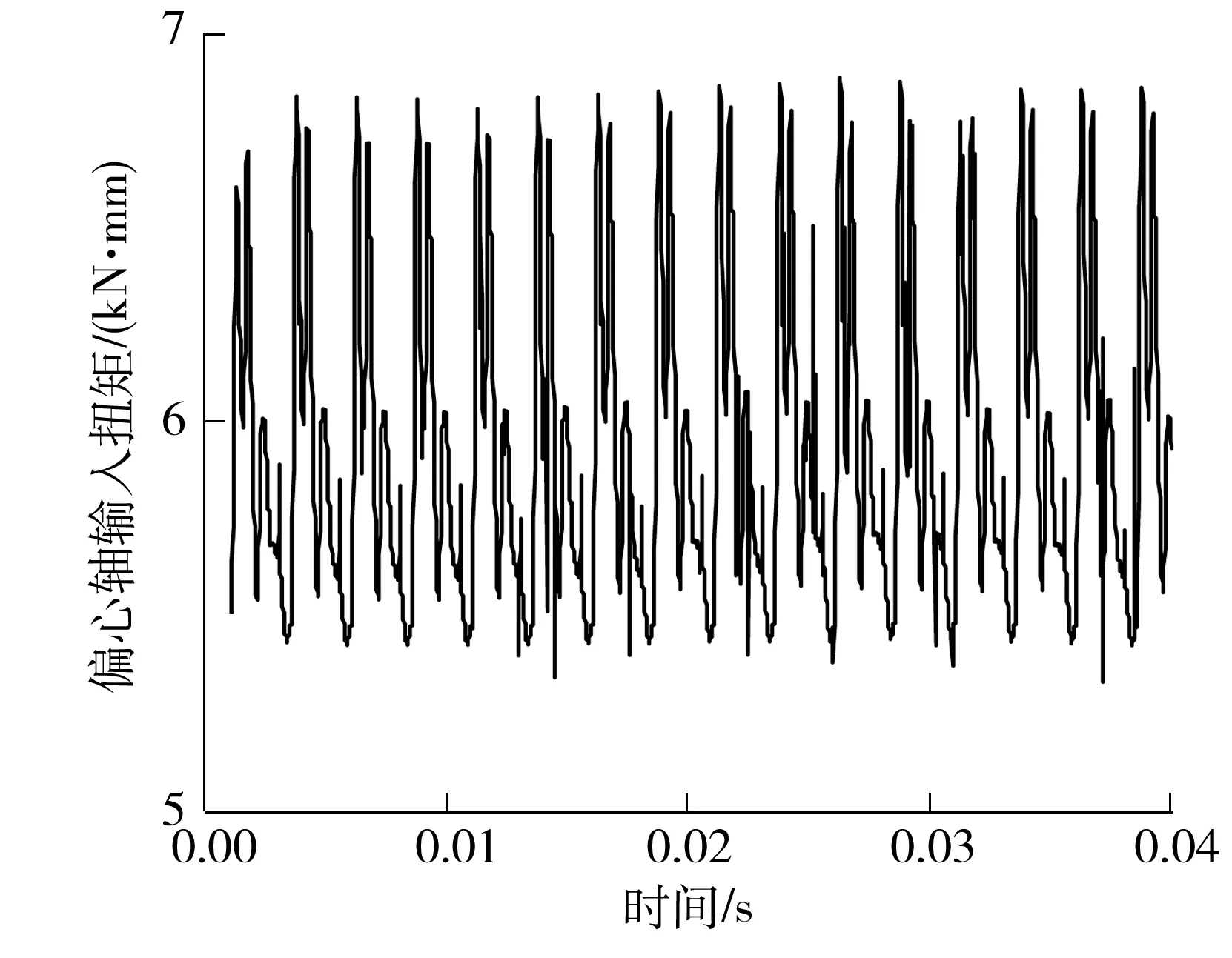
图18 偏心轴输入扭矩

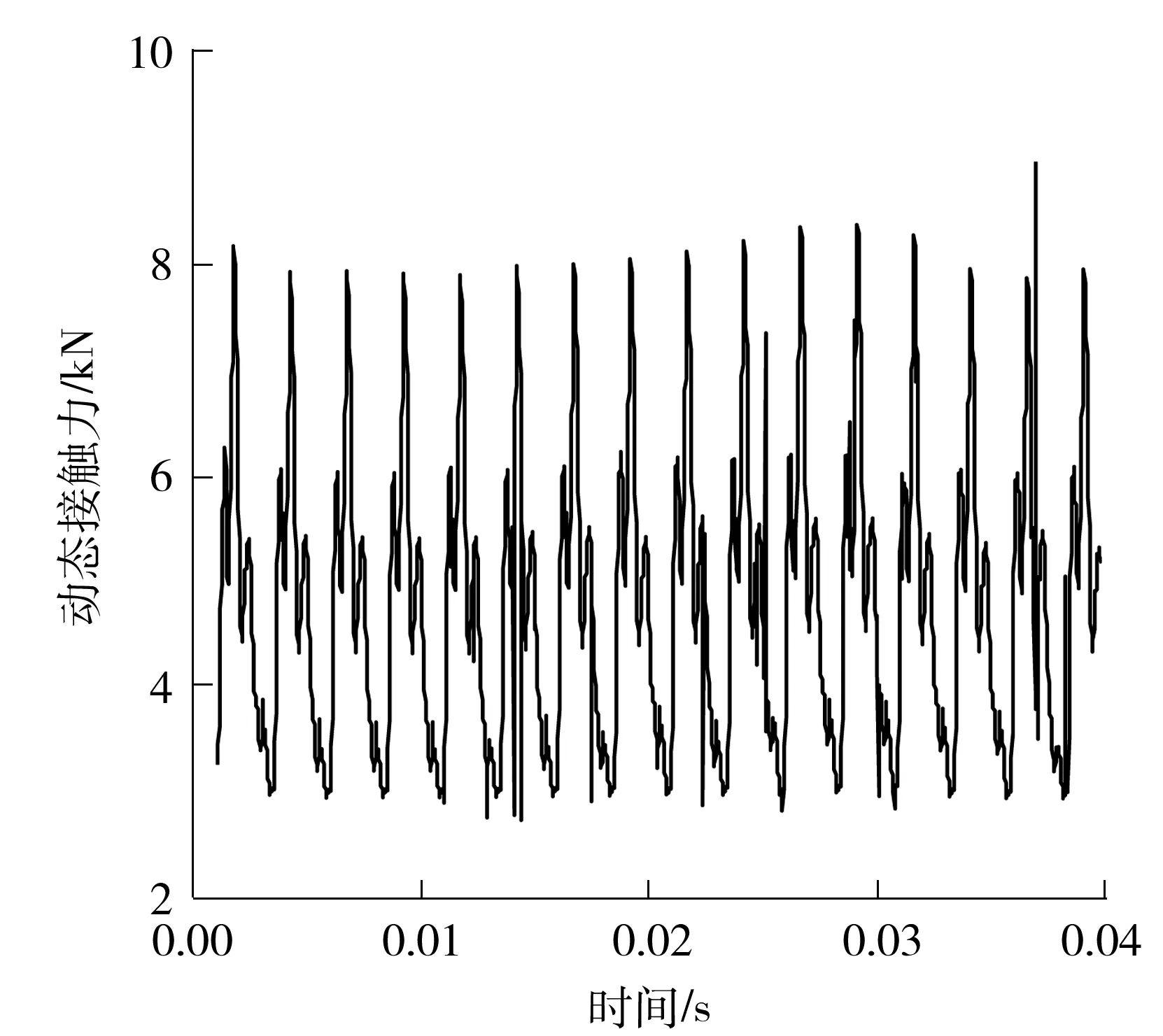
图19 齿轮副动态接触力

图19为齿轮副动态接触力,由图可以看出碰撞力呈周期性变化,周期约为0.002 5 s,与复合摆线轮啮合频率相对应.

5 结论

(1)复合摆线内齿轮上只有一段齿廓参与实际啮合,并且参与啮合的齿廓段长度随着c2的减小而减小;共轭行星轮压力角比相同外形尺寸的普通摆线轮压力角小,并且通过调节齿形参数c2,可进一步减小齿廓主要传动区域压力角,提高传动性能;复合摆线齿轮副诱导法曲率小,承载能力和润滑特性好.

(2)复合摆线齿轮副作少齿差行星传动时存在多齿啮合特性,重合度大,运动传递平稳,具有误差均化效应,传动精度好,并且具有较高的传递效率.

(3)复合摆线齿轮副应用于精密行星传动时,具备优良的传动性能,具有很好的实用开发潜力.文中研究对复合摆线齿轮的实际应用具有理论指导意义.

[1] LITVIN F L,DEMENEGO A,VECCHIATO D.Formation by branches of envelope to parametric families of surfaces and curves [J].Computer Methods in Applied Mechanics and Engineering,2001,190(35):4587- 4608.

[2] VECCHIATO D,DEMENEGO A,ARGYRIS J,et al.Geo-metry of a cycloidal pump [J].Computer Methods in Applied Mechanics and Engineering,2001,190(18):2309- 2330.

[3] CHEN Bing-Kui,FANG Ting-Ting,LI CHAO-YANG,et al.Geometry of cycloid drives [J].Science in China Series E:Technological Sciences,2008,51(5):598- 610.

[4] NAM W K,OH S H.A design of speed reducer with trape-zoidal tooth profile for robot manipulator [J].Journal of Mechanical Science and Technology,2011,25(1):171- 176.

[5] HSIEH C F.A new curve for application to the rotor profile of rotary lobe pumps [J].Mechanism and Machine Theory,2015,87:70- 81.

[6] DEMENEGO A,VECCHIATO D,LITVIN F L,et al.Design and simulation of meshing of a cycloidal pump [J].Mechanism and Machine Theory,2002,37(3):311- 332.

[7] LIU J,CHEN B,MATSUMURA S,et al.Design of a novel cycloid drive with a cycloid-arc gear and analysis of its meshing characteristic [J].Journal of Advanced Mechanical Design,Systems,and Manufacturing,2012,6(2):310- 322.

[8] LI S.Design and strength analysis methods of the trochoidal gear reducers [J].Mechanism and Machine Theory,2014,81:140- 154.

[9] 陈兵奎,刘景亚,李朝阳,等.抛物线型二次包络柱销浮动盘行星传动装置：CN101392814 [P],2009- 03- 25.

[10] 韩振华,石万凯,肖洋轶,等.新型复合摆线外啮合圆柱齿轮副的传动特性分析 [J].西安交通大学学报,2016,50(9):1- 10,131. HAN Zhen-hua,SHI Wai-kai,XIAO Yang-yi,et al.Analysis ontransmission characteristics of novel composite cycloid cylindrical gears for external driving [J].Journal of Xi’an Jiaotong University,2016,50(9):1- 10，131.

[11] 李特文.齿轮几何学与应用理论 [M].上海:上海科学技术出版社,2008.

[12] LITVIN F L,FENG P H.Computerized design and generation of cycloidal gearings [J].Mechanism and Machine Theory,1996,31(7):891- 911.

[13] 昊序堂.齿轮啮合原理 [M].陕西:西安交通大学出版社,2009:193- 201.

[14] 黄中华,张晓建,周玉军.渐开线齿轮啮合碰撞力仿真 [J].中南大学学报(自然科学版),2011,42(2):379- 383. HUANG Zhong-hua,ZHANG Xiao-jian,ZHOU Yu-jun.Simulation of contact force of involute gear meshing [J].Journal of Central South University(Science and Technology),2011,42(2):379- 383.

[15] 毕凤荣,崔新涛,刘宁.渐开线齿轮动态啮合力计算机仿真 [J].天津大学学报,2005,38(11):991- 995. BI Feng-yong,CUI Xin-tao,LIU Ning.Computersimulation for dynamic meshing force of involute gears [J].Journal of Tianjin University,2005,38(11):991- 995.

[16] 李三群,贾长治,武彩岗,等.基于虚拟样机技术的齿轮啮合动力学仿真研究 [J].系统仿真学报,2007,19(4):901- 904. LI San-qun,JIA Chang-zhi,WU Cai-gang,et al.Dynamic simulation study of gear meshing based on virtual prototyping technology [J].Journal of System Simulation,2007,19(4):901- 904.

Analysis of Meshing Properties of Composite Cycloid Planetary Driving with Small Teeth Difference

SHIWan-kaiXULangHANZhen-huaCHANGShuai

(State Key Laboratory of Mechanical Transmission, Chongqing University 400044, Chongqing, China)

By using the composite cycloid with good adjustable geometric feature as the internal gear tooth profile and on the basis of differential geometry and gear conjugate engagement theory, a meshing equation and a conjugate profile equation of composite cycloid planetary driving with small teeth difference are established, and the line of action, the contact ratio, the mesh boundary as well as the non-undercutting condition are all derived. Then, the induced normal curvature and the pressure angle are analyzed, and the influence of tooth profile adjustment coefficient on the pressure angle is discussed. Finally, a three-dimension solid model of the composite cycloid gear pairs is established, and a dynamic simulation is performed to reveal the meshing relationship as well as the transmission efficiency under certain conditions. The results show that the composite cycloid planetary driving with small teeth difference may result in excellent meshing properties such as multi-teeth meshing, small pressure angle, small induced normal curvature and high transmission efficiency.

composite cycloid; small teeth difference; planetary transmission; engagement theory; meshing pro-perties

2016- 06- 07

国家重点基础研究发展计划(973计划)项目(2014CB046304);国家自然科学基金资助项目(51675061) Foundation items: Supported by the National Program on Key Basic Research Project of China(973 Program)(2014CB046304 ) and the National Natural Science Foundation of China(51675061)

石万凯(1968-)，男，博士，教授,主要从事机械创新设计理论与方法、齿轮传动润滑与表面工程、传动失效机理研究.E-mail:wankai_shi@cqu.edu.cn

1000- 565X(2017)02- 0066- 09

TH 132.41

10.3969/j.issn.1000-565X.2017.02.010